超深井上部大尺寸井眼稳定器接头母扣失效机制

2021-09-27李少安王居贺秦垦王文昌陈锋狄勤丰

石油钻采工艺 2021年3期

李少安王居贺秦垦王文昌陈锋狄勤丰

1.中国石化西北油田分公司石油工程技术研究院；2.中国石化缝洞型油藏提高采收率重点实验室；3.上海大学力学与工程科学学院；4.上海大学机电工程与自动化学院

顺北区块是中石化的一个重点探区，油气资源丰富，近年来出现一批井深超8000 m的超深井，如顺北鹰1 井(8 588 m)、顺北5-5H 井(8 520 m)、顺北蓬1 井(8 455.8 m)等，为我国深部油气资源的钻探做出了重要贡献。由于井超深，地质结构和岩性复杂，必须采用多层井身结构，其中，上部Ø444.5 mm井眼是主力井段，长达5 000 m。

为了提速、控斜并降低井壁掉块诱导的卡钻风险，现场施工中采用了带直螺杆的单稳定器钟摆BHA，但在所钻的7 口超深井中，有3 口井稳定器母扣断裂，1 口井直螺杆母扣断裂。稳定器的断裂位置基本位于母扣大端第3～4 扣(距离母扣端面10.0～11.0 cm)处。失效时所用钻压60.0～80.0 kN，所用转速约55.0 r/min。研究结果表明，所用稳定器的材质、加工质量都满足要求，不是引起稳定器母扣端螺纹接头失效的主要原因。

为确保后续钻井作业安全，结合钻柱动力学特性宏观分析和稳定器母扣端螺纹接头局部应力分析，探讨了大尺寸井眼稳定器母扣的失效机制。

1 钻柱动力学有限元模型

长期以来，钻柱的动力学特性研究受到许多专家学者的关注。这方面的研究包括2 个方面：一方面是BHA 的振动问题，如T.M.Burgess 等人［1］研究了BHA 的横向振动，首先用静力学方法求解BHA 的上切点位置，随后对切点以下钻具的振动特性进行有限元分析；胡以宝等［2］研究了带旋转导向工具底部钻具组合的动力学特性分析及参数优化。另一方面是全井钻柱的动力学特性研究，如M.W.Dykstra［3］采用有限元法对全井钻柱进行静力学分析，利用Newmark 方法对全井钻柱进行瞬态动力学分析，发现BHA 是横向振动的主要部分。胡以宝、狄勤丰等［4-5］利用节点迭代法实现了全井钻柱的动力学特性分析，并进行了钻柱动态安全性的研究。李子丰、刘清友、祝效华等对全井钻柱动力学开展了较深入的分析研究［6-8］。这些研究有力地促进了钻柱力学研究和钻井技术的进步。

由于钻柱在井下的运动和受力状态十分复杂，需要考虑其超细长比和双重非线性特征。基于Lagrange 方程，可以建立钻柱动力学有限元模型［4-5］

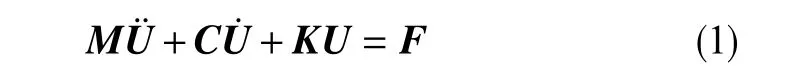
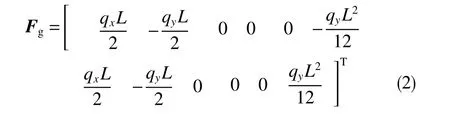
式中，qx和qy分别为钻柱浮重在x轴(沿井眼轴线指向井底)方向的分量和y轴(沿井眼高边)方向的分量，qx=qcosα,qy=qsinα；q为钻柱单位长度浮重，N/m；α为钻柱单元的轴线与垂直方向的夹角，rad；L为单元长度，m。

不平衡力为

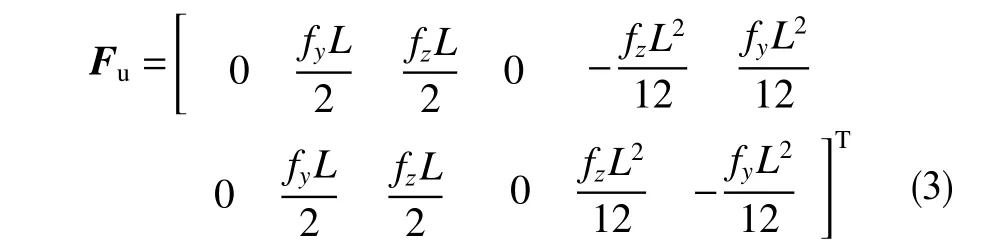
式中，fy和fz分别为不平衡力沿y轴和z轴(与x轴和y轴组成坐标系)的分量，可表示为

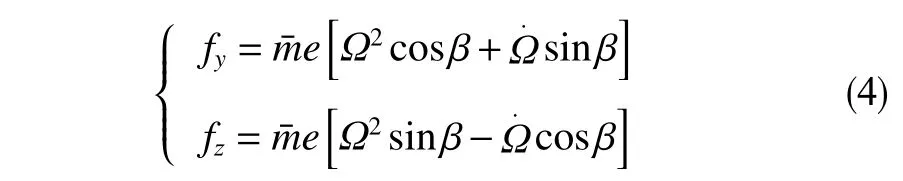
在有限元模型(1)中，刚度矩阵已包含钻柱的变截面特征，但鉴于大尺寸井眼中稳定器与钻铤外径相差较大，尤其在弯曲井段或井眼全角变化率大的井段，当BHA 受拉或受压时，都将因截面的变化而引起初始弯矩的变化，如图1 所示。

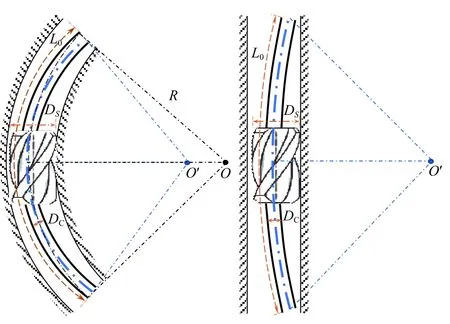
图1 稳定器变截面产生的弯曲放大效应Fig.1 Bending amplification effect caused by variable cross-section of stabilizer

稳定器本体外径有尺寸限制(需尽可能与钻铤一致)，因此井径越大，稳定器直径与其本体外径的差异越大，相应的附加弯曲效应将越明显。若考虑不可避免的钻柱与井壁碰摩引起的动态冲击效应，这种附加弯曲效应将更严重，且具有动态变化特征。变截面引起的附加弯矩TM可通过建立在弯矩、剪力和轴向力共同作用下的挠度方程及几何关系得到［9］

结合式(2)～(5)，单元外力矩阵Fe最终表示为

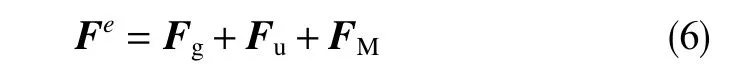
考虑到钻柱超长，且长细比很大，利用节点迭代法和Newmark 法对上述模型进行求解［4-5］，从而获得钻柱不同位置的动力学特性，包括涡动速度、动态弯矩和应力等。

2 钻柱动力学特性分析及稳定器螺纹接头母扣端动态载荷确定

以顺北XX 井为例进行分析。该井是顺北油田的一口垂直探井，Ø444.5 mm 井眼的长度为4 218.0 m，钻进至井深2 274.0 m 时，稳定器母扣断裂，断口距母扣台肩10.00 cm，此时采用的钻具组合为：

Ø444.5 mmPDC 钻头×0.5 m+Ø286.0 mm 直螺杆×9.6 m+Ø279.4 mm 钻铤×9.2 m+Ø441.0 mm 稳定器×2.3 m+Ø241.3 mm 钻铤×47.0 m+Ø203.2 mm 钻铤×56.6 m+Ø139.7 mm 加重钻杆×72.4 m+Ø139.7 mm钻杆×···。

钻井液密度为1.19 g/cm3，钻压80.0 kN，转速55.0 r/min。通过计算可得钟摆段中点和稳定器母扣端的动态弯矩、扭矩及轴向力，见图2～图3。对比图2、图3 可以看出，钟摆段中点的动态轴向力在−105.2～−25.9 kN 之间变化，稳定器母扣端处的动态轴向力在−40.1～39.0 kN(负为受压)之间变化。不难发现，稳定器母扣端的动态轴向力在0 值附近波动，与“静态中和点”位置较吻合。

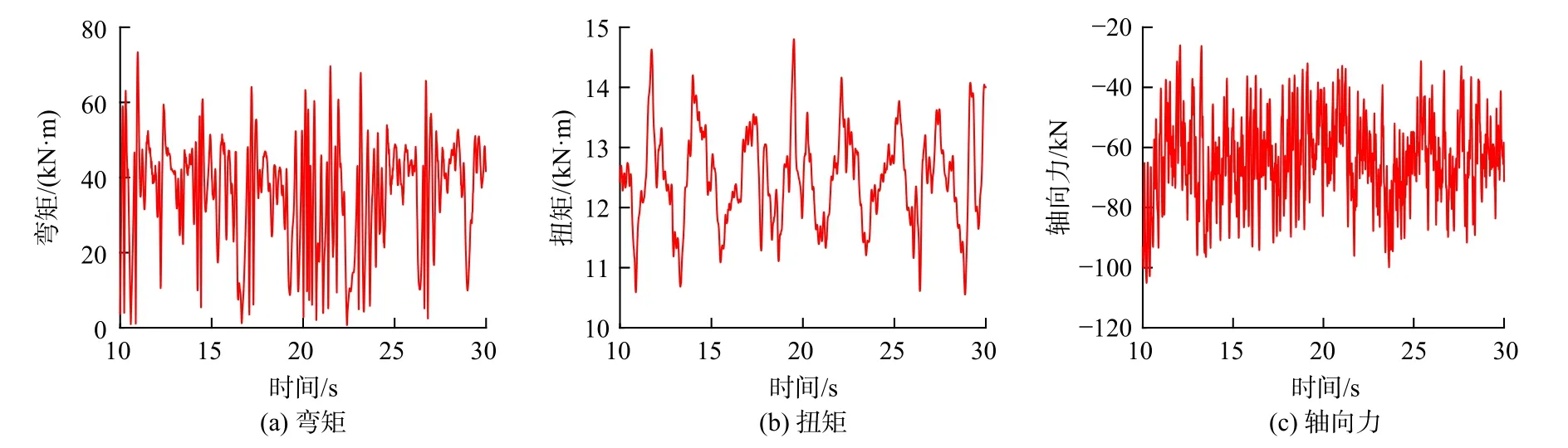
图2 钟摆段中点处的动态载荷Fig.2 Dynamic load at the midpoint of the pendulum segment

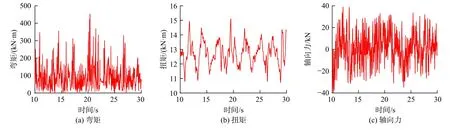
图3 稳定器母扣端截面处的动态载荷Fig.3 Dynamic load at the box of stabilizer's threaded joint

稳定器母扣端处动态扭矩在10.8～15.1 kN·m 间波动，相较于钟摆段中点处的动态扭矩(10.6～14.7 kN·m)，整体变化较小，说明在井深2 274.0 m 时，钻柱的扭转振动较弱。而最为显著的是，稳定器母扣端动态弯矩在0～453.0 kN·m 间变化，与钟摆段中点相比，虽然动态载荷变化都很大，但前者的动态弯矩明显大于后者，且变化频率更高，此变化主要缘于大变截面引起的附加弯曲效应。

稳定器两端和钟摆段中点3 个位置的涡动轨迹、涡动速度和宏观动态应力见图4～图5。

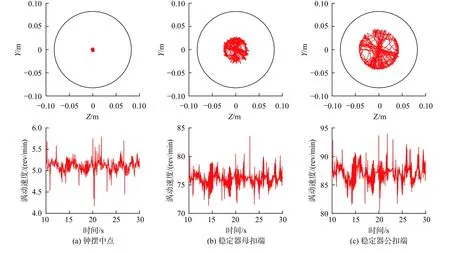
图4 钻具在3 个位置处的涡动轨迹和涡动速度Fig.4 Whirl trajectory and whirl velocity of the drill tool at three locations

图5 钻具在3 个位置处的动态应力Fig.5 Dynamic stresses of the drill tool at three locations

从图4 中可以看出，3 个位置的钻铤均不与井壁发生碰撞，钟摆段中点基本位于井眼中心，涡动速度较小；稳定器两端涡动速度较高，稳定器母扣端涡动速度最大值约93.9 r/min，平均约87.0 r/min；稳定器公扣端涡动速度最大达83.6 r/min；平均约76.0 r/min。稳定器母扣端、公扣端涡动轨迹和涡动速度存在差异主要源于缘于钻柱运动的影响。从图5 中可看出，钟摆段中点处的Mises 应力在0.6～70.5 MPa范围变化，平均约36.9 MPa；稳定器母扣端的Mises应力在3.0～425.3 MPa 范围变化，平均约88.4 MPa；稳定器公扣端的Mises 应力在0.8～255.2 MPa 范围变化，平均约83.5 MPa。3 个位置钻具的Mises 应力以弯曲应力为主，轴向应力和扭转应力所占比例较小，且变化不大。稳定器母扣端的动态弯曲应力最大值是钟摆段中点最大应力的6.5 倍，平均值为其2.3 倍。稳定器母扣端的动态弯曲应力同样高于公扣端，最大值是公扣端动态弯曲应力最大值的1.7 倍，平均值接近(约3%)。

该井段井斜变化率较小，为0.5（°）/30 m，因此，动态弯曲应力很大的原因主要是由于稳定器与井壁发生碰撞时，稳定器的大尺寸变截面特征产生的附加弯曲效应造成。而稳定器两端的动态弯曲应力平均值接近，以及最大值相差较大，也说明了稳定器上下钻具的运动存在差异。这从图4 中也可看出，稳定器母扣端的涡动速度高于公扣端涡动速度。同时，3 口井稳定器母扣发生断裂，而公扣无一损坏，也能初步说明这一特征。

3 大尺寸井眼稳定器螺纹接头的三维应力特征和失效机制

为进一步分析稳定器母扣失效机制，建立稳定器母扣端螺纹接头有限元模型以计算分析其在动态载荷作用下的局部应力分布特征。钻具接头公扣与母扣的接触面是一个复杂空间螺旋曲面，其受力分析涉及材料非线性、几何非线性和接触非线性，解析求解非常困难。目前主要采用数值模拟的方法进行求解，但目前普遍采用的二维轴对称有限元分析由于忽略了螺纹的螺旋升角，难以评价上扣扭矩、轴向拉力、工作扭矩等复杂工况条件下钻具接头的受力特征［10］。本文采用三维有限元模型，基于ABAQUS进行钻具接头三维应力特征分析，以充分反映螺纹的螺旋升角、上扣扭矩及复杂载荷的影响［11］。

稳定器母扣与钻铤公扣啮合的有限元模型如图6 所示。稳定器母扣端螺纹接头模型共有53.5 万个单元，58.4 万个节点。根据上文所计算的动态载荷确定计算载荷：轴向力−40.0 kN(压缩)，工作扭矩15.0 kN·m，弯矩453.0 kN·m。计算过程中首先对稳定器母扣端螺纹接头施加142.5 kN·m 的上扣扭矩，然后依次施加上述载荷。

图6 稳定器接头母扣端螺纹接头有限元模型Fig.6 Finite element model of the box end of stabilizer thread joint

图7 给出了弯矩作用前后稳定器母扣端螺纹接头的Mises 应力分布规律。从图7(a)可看出，上扣扭矩、轴向力和工作扭矩作用下公扣大端、母扣镗孔及台肩啮合处应力水平较高，主要是因为上扣扭矩的作用实现了接头丝扣预紧，使该处应力较高。而图7(b)表明在弯矩作用下母扣大端螺纹牙处应力变化较大，Mises 应力水平有较大幅度上升，而公扣大端和台肩啮合面处应力水平则相对比较稳定。

图7 弯矩作用前后稳定器接头母扣端螺纹接头Mises 应力分布规律Fig.7 Mises stress distribution of the box end of stabilizer thread joint before and after bending moment

图8 为弯矩施加过程中稳定器母扣端螺纹接头各关键部位应力变化。图9 为动态弯矩变化引起的稳定器母扣螺纹牙处的应力波动。

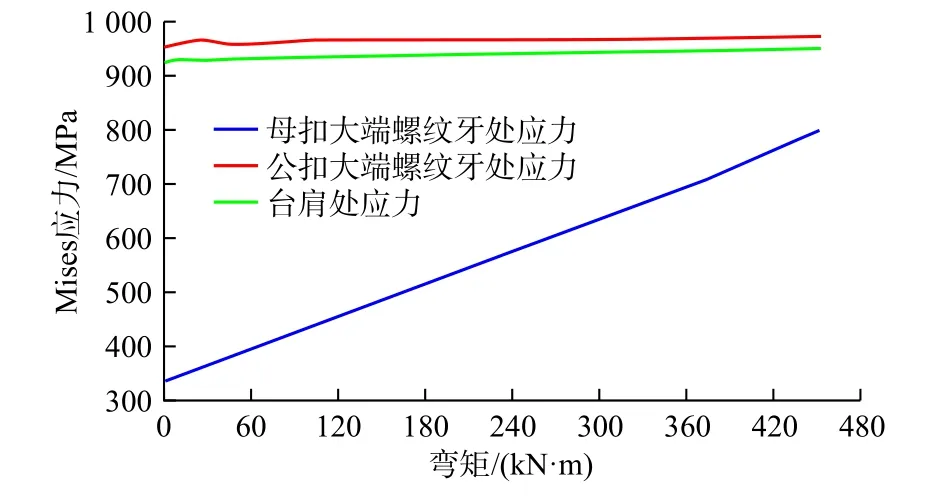
图8 稳定器接头母扣端螺纹接头关键部位Mises 应力变化Fig.8 Mises stress variation at key points of the box end of stabilizer threaded joint

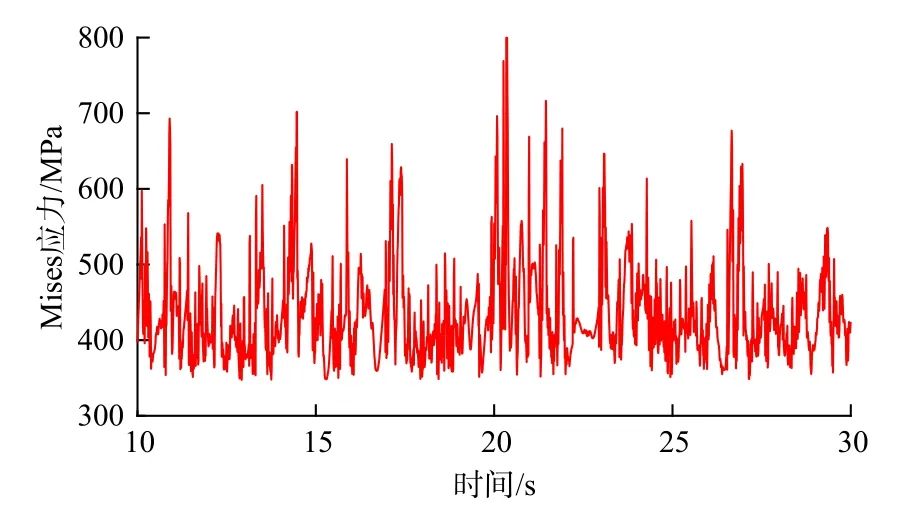
图9 动态弯矩变化引起的稳定器母扣端螺纹接头的应力波动Fig.9 Stress fluctuation of the box end of stabilizer thread joint caused by dynamic bending moment variation

从图8 和图9 中可见钻铤公扣大端螺纹牙处和台肩啮合处应力水平虽然较高，但变化较小，介于951.5～973.1 MPa 之间，变化幅度仅为21.6 MPa。而动态弯矩作用形成的母扣根部螺纹牙(第2～5 扣)最大Mises 应力高达799.1 MPa，虽然小于与其啮合的钻铤公扣根部螺纹牙的应力(约973.1 MPa)，但其变化幅度高达465.0 MPa，变化频率达22.0 Hz。这种高频大幅度应力变化极易引发稳定器母扣大端螺纹牙疲劳失效。事实上，3 口井的稳定器母扣断裂位置都位于母扣大端第3～4 扣。