初中生认知需求与数学学业成绩的关系:基于潜在剖面分析*
2021-09-27史滋福唐婉秋谢云天
史滋福 唐婉秋 谢云天
(1 湖南师范大学心理学系,认知与人类行为湖南省重点实验室,长沙 410081) (2 长沙师范学院应用心理学教研室,长沙 410100)
1 引言
数学作为科学技术的基础、人类思维的表达方式,对个体的职业发展和学术成就有着深远的影响(Ceci,Williams,& Barnett,2009)。而数学成绩作为学生学业成就的主要组成部分,不仅是国内外大型教育质量评价项目(Third International Mathematics and Science Study,TIMSS;Program for International Student Assessment,PISA)持续关注的重点内容(黎亚军,2016),也是检查数学学习质量的重要依据(康玥媛,张楠,王光明,佘文娟,刘艳云,2016)。
数学学习涉及解决复杂问题,因此,研究认为认知因素与数学学业成绩有很强的关联(Maloney & Retanal,2020)。研究者认为与智力有关的数学运算、工作记忆和类比推理等与数学成绩均显著正相关(郝嘉佳,陈英和,陈艺萍,白学军,2017)。然而,有研究发现,在智力水平相当、学习环境一致的情况下,学生的数学学习表现仍然差异显著(王光明,佘文娟,宋金锦,2014)。康玥媛等人(2016)认为,高效数学学习心理特征的结构要素不仅包含基本认知能力和学习策略,还包含非智力因素。
认知需求(need for cognition,NFC)作为一种与问题解决有关的非智力因素(Heppner,Reeder,& Larson,1983),是个体主动参与和享受思考的一种稳定的个人特质(Cacioppo & Petty,1982)。认知需求与大脑的灵活性密切相关,通常对各种认知活动(如创造力)有积极的影响(He et al.,2019)。高认知需求的学生往往对其自身解决问题的能力有积极的评价,更喜欢复杂的数学任务,与更好的学业成就相关联(Sadowski & Gülgös,1996)。事实上,认知需求作为一种“饥饿思维”,是“决定个人学业成绩差异的核心因素”(Von Stumm,Hell,& Chamorro-Premuzic,2011)。近年来,研究者通过对10 到16 岁的中小学生进行调查,发现认知需求的个体差异与学业成绩有关(Luong et al.,2017),尤其在标准化测试中,高认知需求的学生有更好的学业成绩(Neigel,Behairy,& Szalma,2017)。具有高认知需求的学生更有可能参加需要个人天赋的课程(Meier,Vogl,& Preckel,2014),并在学业测试中取得更高的分数(Elias & Loomis,2002)。一项对德国学生的研究甚至还发现,认知需求在智力与平均绩点(grade point average,GPA)的关系中起调节作用,在较高的认知需求分数下,个人推理能力与GPA 的关系减弱,表明认知需求具有补偿效应(Strobel,Behnke,Gärtner,& Strobel,2019)。
近年来,在由无意识的自动化加工和有意识的控制加工所组成的双加工模型(Evans,2003)基础上,Stanovich,West 和Toplak(2011)将有意识的类型二加工进一步划分为算法心智和反省心智,并从理性思维的角度提出了“三重加工心智模型”。该模型认为,人类大脑同时具备三种心智:自主心智、算法心智以及反省心智。其中,算法心智关注的是认知机制中的计算加工过程,反省心智则通过发起压制来要求算法心智采取理性行动,其衡量指标是思维倾向。理性的概念内涵包含反省心智的思维倾向以及算法心智的效率(基思·斯坦诺维奇,2015)。认知需求作为一种乐于思考的思维倾向,不仅反映了个体加工信息的认知努力程度,还影响问题解决和决策(Furnham & Thorne,2013),以及个体对信息加工类型的选择(Bertrams & Dickhäuser,2009)。认知需求的差别反映了反省心智的个体差异(Stanovich et al.,2011)。研究表明,与低认知需求的个体相比,高认知需求的个体会将其判断和信念建立在经验信息和理性思考的基础上(Leary,Shepperd,McNeil,Jenkins,& Barnes,1986)。此外,数学理性思维是数学核心素养的基础,只有在理性思维的指引下,才能促进数学素养的发展,从而更好地解决数学问题(宁锐,李昌勇,罗宗绪,2019)。已有研究缺乏从理性思维的角度深入揭示认知需求与数学学业成绩的关系。初中阶段的青少年正处于心智发展的重要时期,更需要认知需求来督促学习。有鉴于此,本研究试图基于三重加工心智模型探讨认知需求与初中生数学学业成绩的关系。
此外,以往研究大多认为,认知需求是高与低的两极变量,根据个体在量表上得分的中位数来进行划分(Neigel et al.,2017),但徐洁和周宁(2010)认为这种划分方法不仅在取样有偏差时,划分也会出现偏差,而且这种划分方法往往忽略了学生群体的内部异质性(杨亚威,张敏强,漆成明,2017)。然而,有研究者认为认知需求可能存在多个维度,Tanaka,Panter和Winborne(1988)认为认知需求结构可划分为三类:认知持久性、认知复杂性和认知信心。Lord 和Putrevu(2006)通过三个探索性研究揭示了认知需求量表的四个维度:认知刺激的享受、复杂性偏好、认知努力的承诺以及对理解的渴望。事实上,徐洁和周宁认为,不同认知需求者在面对复杂的认知活动时的表现差异还体现在对认知活动的投入程度和喜爱程度上,对个体信息加工倾向性的影响也是多方面的。可见,研究者已认识到认知需求存在异质性,但不同质群体的划分是潜在的,在分组变量不明确的情况下,需要基于模型的方法对潜在分组进行估计。而潜在剖面分析(latent profile analysis,LPA)以个体为中心,对认知需求的潜结构进行分析,进而探索群体内部的异质性分类模式(张洁婷,焦璨,张敏强,2010;Notelaers,Einarsen,De Witte,& Vermunt,2006)。因此,本研究认为:认知需求存在不同的潜在类别,且不同类别的认知需求与数学学业成绩的关系存在显著差异。
2 研究方法
2.1 被试
以班级为单位,选取江西省三所公立中学的初中生。发出问卷2956 份,剔除漏答过多和有规律作答的问卷后(刘豆豆,陈宇帅,杨安,叶茂林,吴丽君,2020),收回有效问卷2844 份。其中,男生1551 名(54.54%),女生1293 名(45.46%)。初一学生947 名(33.30%),初二学生979 名(34.42%),初三学生918 名(32.28%)。被试的平均年龄为13.58±1.01 岁。
2.2 研究工具
2.2.1 认知需求量表
采用Kokis,Macpherson,Toplak,West 和Stanovich(2002)修订的认知需求量表(Need for Cognition Scale)。该量表共9 题,为单一维度结构。采用4 点计分,1 表示“非常同意”,4 表示“非常不同意”。得分越高,表示认知需求越高。该量表在本研究中的Cronbach’s α 系数为0.71。参照徐洁和周宁(2010)对认知需求的定义和内涵,本研究将认知需求划分为两个维度。第一个维度是认知喜爱,均涉及喜欢思考问题,为第1 至第5题,采用反向计分;第二个维度是认知投入,均涉及信息加工倾向,为第6 至第9 题,采用正向计分。
2.2.2 数学学业成绩
来自最近一次期中考试的数学成绩,并参照陈京军、吴鹏和刘华山(2014)的研究,将数学成绩在各自学校的相应年级内标准化,转化为标准分。
2.3 程序
由经过前期培训的班主任主持调查,利用班会时间集中发放问卷,学生理解要求后独立回答,随后当场回收。整个任务持续约15 分钟。问卷回收后,应用SPSS25.0、Mplus7.4 统计软件对数据进行分析。
3 结果
3.1 主要变量的相关矩阵
主要变量的Pearson 相关分析结果显示(见表1),性别(1=男,0=女)和认知需求、数学学业成绩的相关均未达到显著水平,ps>0.05。认知需求和数学学业成绩显著正相关,p<0.001。

表1 主要变量的Pearson 相关矩阵
3.2 初中生认知需求的潜在剖面分析结果
以因素分析得出的两个维度上的得分作为外显变量,建立潜在剖面模型,对初中生的认知需求进行潜在剖面分析的模型拟合性估计。在潜在剖面模型分析中,AIC 和BIC 越低,Entropy 越高,且LMRT 和BLRT 达到显著,模型的拟合度越高,模型更优(张洁婷等,2010)。根据不同类别的潜在剖面分析拟合指数结果(见表2),4 类别模型的AIC、BIC、aBIC 均低于3 类别模型,Entropy 比3 类别及5 类别模型更高,且LMR-LRT 和BLRT显著。而3 类别模型Entropy 的值偏小,且AIC 和BIC 偏大。另外,5 类别模型的LMR-LRT 和BLRT均不显著。所以,选择4 类别模型是比较合适的,其拟合数据最佳(参见表2)。

表2 初中生认知需求潜在剖面分析拟合信息
从图1可知,四个类别的条件均值显现出不同的特征。在四种类型中,类别1 在认知喜爱维度上的得分居中,而在投入维度上得分偏低,故被命名为“参与思考–低投入型”,占所有被试的25.52%;类别2 在各条目上的得分均属于中等水平,故被命名为“参与思考–一般投入型”,占所有被试的40.58%;类别3 在认知喜爱维度上得分最低,而在认知投入维度上得分偏高,故被命名为“懒于思考–高投入型”,占所有被试的3.87%;类别4 在两个维度上得分均偏高,故被命名为“喜欢思考–高投入型”,占所有被试的30.03%。
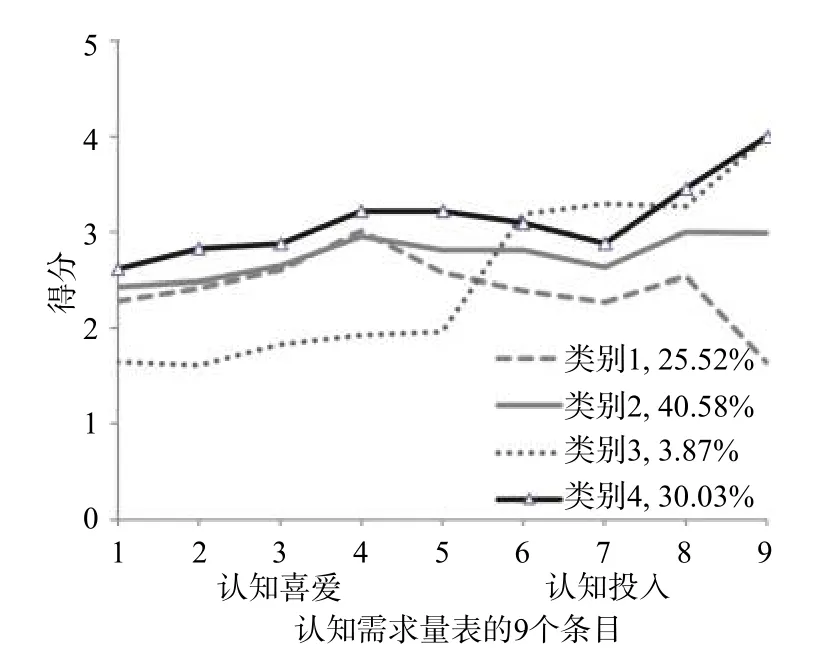
图1 初中生认知需求四个潜在类别的估计条件均值
3.3 认知需求潜在类别对人口学变量的多项Logistic回归
为了进一步探讨认知需求类别的性别和年级效应,以便更好地发现认知需求的分布特点,继续以潜在类别为因变量(类别4 喜欢思考–高投入型为比较参考类别),年级(初三为参照)、性别(女性为参照)作为自变量,进行多项Logistic回归分析。结果显示(参见表3),年级对认知需求潜在类别的影响显著,与初三学生相比,初一学生和初二学生在类别1(参与思考−低投入型)、类别2(参与思考−一般投入型)、类别3(懒于思考−高投入型)的回归系数B值为负值且差异显著,表明这两个年级的学生更可能是喜欢思考−高投入型。性别对认知需求潜在类别的影响不显著。

表3 认知需求潜类别组对人口学变量的多项Logistic 回归
3.4 不同认知需求潜在类别初中生的数学学业成绩比较
考虑到已有研究表明性别、年级和数学学业成绩相关(刘蕴坤,陶沙,2012),因此,本研究以认知需求潜在类别为自变量,以性别和年级为协变量,数学学业成绩为因变量,进行单变量方差分析。结果显示,不同认知需求类别初中生的数学学业成绩差异显著,F(3,2838)=29.62,p<0.001,η=0.03。多重比较结果显示,参与思考–低投入型初中生的数学学业成绩(−0.20±1.01)既显著低于参与思考–一般投入型(−0.05±0.98),p<0.01,也显著低于喜欢思考–高投入型(0.25±0.97),p<0.001;参与思考–一般投入型(−0.05±0.98)和懒于思考–高投入型(−0.11±1.01)均显著低于喜欢思考–高投入型(0.25±0.97),ps<0.001。
4 讨论
4.1 初中生认知需求的潜在剖面分析
本研究首次采用潜在剖面分析对认知需求进行划分,最终确定为4 类别模型,分别是:参与思考–低投入型、参与思考–一般投入型、懒于思考–高投入型、喜欢思考–高投入型。其中,参与思考–一般投入型的学生对思考问题表现出一定的热情和投入,所占人数比例最多(40.58%),表明多数学生的认知需求处于中等水平;懒于思考–高投入型的人数比例最少(3.87%),说明仅有少数学生不愿思考复杂问题,而愿意投入到简单问题的解决,这也启示教育工作者在教学中可以通过引导学生积极思考问题,将这类学生的认知需求转化为喜欢思考–高投入型;另外,懒于思考–低投入型学生的认知喜爱和投入的程度均偏低,不愿钻研复杂问题,在教学中可将其作为重点关注对象,引导其建构良好的认知需求。
本研究通过多项Logistic 回归分析探讨了认知需求类别的性别和年级效应,发现年级影响初中生的认知需求潜在类别,而性别对认知需求潜在类别的影响不显著。与初三学生相比,初一学生和初二学生更可能是喜欢思考–高投入型。说明不同学龄阶段的青少年认知需求存在差异,随着年级的升高,认知需求有下降的趋势。究其原因,青少年期处于自我同一性形成与同一性混乱相冲突的时期,易受外界因素干扰。到了初三阶段,各科学习任务不断加重,特别是数学知识的难度加大,学生的数学焦虑感最为明显(Wigfield & Meece,1988);另外,有研究发现,初三学生的数学学业能力自我概念显著低于另两个年级,易产生消极学业情绪(陈京军等,2014)。
4.2 认知需求与数学学业成绩的关系
根据方差分析结果发现,不同认知需求类别的初中生的数学学业成绩差异显著,且认知需求与数学学业成绩显著正相关,与以往的研究结果一致(Elias & Loomis,2002;Neigel et al.,2017)。参与思考–低投入型初中生的数学学业成绩既显著低于参与思考–一般投入型,也显著低于喜欢思考–高投入型。这表明认知需求不强烈的学生表现出认知喜爱和认知投入程度都偏低,其数学学业成绩也更差。这是由于这类学生作为“认知吝啬鬼”,他们缺乏努力思考的内在动机,依赖于他人、认知启发或社会比较过程来理解事物(Ganuthula & Dyaram,2016),通常会避免从事要求认知能力高的活动,在学习上不愿花费更多的认知资源(Schindler,Schindler,& Reinhard,2019)。其次,参与思考–一般投入型初中生的数学学业成绩也显著低于喜欢思考–高投入型。说明在反省心智的作用下,认知需求越强烈的学生在面对问题时,能够表现出更享受思考并努力投入的学习状态,有助于提高学业质量,从而数学学业成绩表现更佳。最后,懒于思考–高投入型初中生的数学学业成绩也显著低于喜欢思考–高投入型。该结果表明,面对复杂的数学问题时,认知难度增大,不仅要做到高投入,也要从内在动机上构建喜欢思考的认知倾向,才能有助于提高学业成绩。因此,在发挥算法心智的功能时要重视反省心智的作用,塑造理性思维,提高学生的认知喜爱和认知投入程度,构建良好的认知需求水平,从而提升数学学业成绩。
另外,性别和数学学业成绩的相关未达到显著水平,这与以往的研究结果不一致(董博,2019;林崇德,1996)。造成不一致的原因可能是:(1)被试来源的差异;(2)不同的统计分析方法。例如,董博为了探讨影响数学成绩的因素及其性别差异,在全国范围内取样,但仅随机抽取了初一和初三学生,采用逐步回归法建立模型来进行分析。而本研究选取的被试是来自江西省的三所中学,涵盖了三个年级,采用相关分析方法来探讨性别与认知需求、数学学业成绩的关系。
4.3 研究不足与展望
本研究中所使用的数据来源是初中生的自我评价,可能会受到社会赞许性的影响,未来研究可以采用360 度测评的方法收集数据,丰富数据来源,增强结果的可信度(刘丹,缴润凯,王贺立,李飞飞,2018)。还有,认知需求作为一种思维倾向,仍有学生的认知需求水平不稳定,在纵向追踪研究中,认知需求可能会转化为其他组,可进一步做潜在类别转换分析。同时,也可以从纵向研究的角度对认知需求和数学学业成绩的关系进行研究,并且可进行内在机制的探讨,以便更好地验证三重加工心智模型。
5 结论
(1)初中生认知需求具有异质性,包括四个潜在类别:参与思考–低投入型、参与思考–一般投入型、懒于思考–高投入型、喜欢思考–高投入型。(2)初中生的认知需求体现出年级效应,但没有性别效应。(3)不同认知需求类别的初中生具有不同的数学学业成绩。具体而言,喜欢思考–高投入型的数学学业成绩最高,而参与思考–低投入型的数学学业成绩显著低于参与思考–一般投入型和喜欢思考–高投入型初中生的数学学业成绩。
