支撑剂在交叉裂缝中运移规律的数值模拟

曾军胜 ，戴城 ，方思冬 ，李恒 ，刘华

（1.中国石化石油勘探开发研究院，北京 100083；2.中国地质大学（武汉）资源学院，湖北 武汉 430074）

0 引言

近年来，非常规气藏的开发受到越来越多的关注和重视。2020年，我国页岩气产量达到了200多亿立方米，同比增长高达30%，成为天然气增产的主力。这得益于水平井和水力压裂2项关键技术的快速发展和成熟应用。而水力压裂体系涉及一个至关重要的流体-颗粒两相流问题——支撑剂运移［1-3］。采用支撑剂能够有效避免水力裂缝的闭合，从而维持有效传导率。而支撑剂在裂缝中的运移和分布情况，则直接影响水力压裂改造后储层的有效传导率。因此，研究支撑剂运移过程对水力压裂的效果评估和方案设计有重要意义。

通常，支撑剂运移发生在水力压裂产生的复杂缝网当中。如何改善支撑剂在缝网中的铺置效率，使更多的支撑剂进入支缝，成为现场施工方案设计的重点问题。以往大多数的文献主要采用物理实验［4-7］和数值模拟［8-9］这两大类方法研究支撑剂在单一裂缝中的运移规律。考虑的各类因素包括携砂液和支撑剂颗粒的物性参数、施工方案、支撑剂体积分数、裂缝扩展及流体滤失等。这些研究对揭示支撑剂在裂缝中沉降和运移的基本规律具有十分重要的作用。

针对支撑剂在缝网中的运移规律，近年来国内外的相关研究也呈现逐年增长的趋势。Sahai等［10-12］利用物理实验方法，研究了支撑剂在复杂缝网中的运移规律。但是物理实验周期往往较长，同时能够获取的数据十分有限。目前，数值模拟已成为研究支撑剂运移的有效方法。郝丽华等［13-14］采用双流体模型，模拟了大尺度下支撑剂在缝网中的铺置情况。

支撑剂运移本质上是一类流体与颗粒强耦合作用的两相流问题。为了阐明支撑剂运移涉及的物理机制，需要在物理建模时充分考虑其关键机理。在支撑剂运移过程中，支撑剂颗粒之间的作用、裂缝壁面对颗粒的作用、携砂液与颗粒之间的相互作用是十分重要的。本文结合目前流行的流体-颗粒两相流的数值模拟方法，即计算流体力学-离散元方法（Computational Fluid Dynamics-Discrete Element Method，简称 CFD-DEM 方法）［15-16］，对支撑剂在交叉裂缝中的运移过程进行研究，分析裂缝交角及携砂液黏度对支撑剂运移规律的影响。CFD-DEM方法基于拉格朗日框架刻画颗粒的演化，能够准确刻画颗粒与颗粒/壁面及流体与颗粒之间的相互作用。与双流体模型相比，CFD-DEM方法在物理建模上具有天然优势，能够捕捉更多的运移细节。

本文旨在研究支撑剂颗粒在交叉裂缝中的运移机理，包括颗粒堆积、聚团等效应，同时定量考察在不同条件下支撑剂流入支缝的比例，以便直观理解。下面分别从CFD-DEM方法、裂缝交角及携砂液黏度3个方面，对支撑剂在交叉裂缝中的运移规律展开讨论。

1 CFD-DEM方法

1.1 流体及颗粒的控制方程

在CFD-DEM方法中，流体控制方程为体积平均纳维-斯托克斯（VANS）方程［17］：

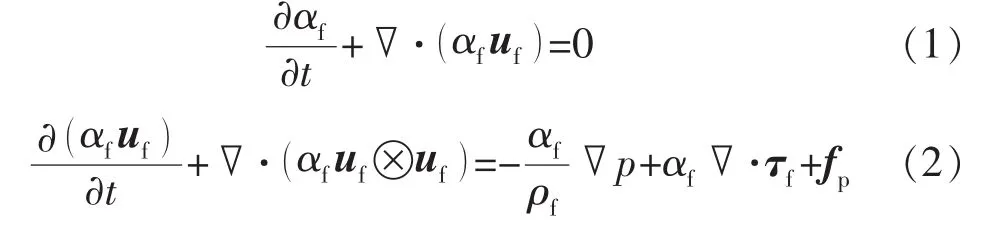
式中：αf为流体体积分数；t为时间，s；▽为梯度算子；▽·为散度算子；uf为流速，m/s；ρf为流体密度，kg/m3；p为流体压力，Pa；τf为流体黏性应力张量，Pa；fp为流体与颗粒相互作用（特指拖曳力）产生的动量源汇项，m/s2。

式（1）和（2）分别为流体的连续性方程和动量方程，这里假设流体为不可压缩牛顿流体。

在CFD-DEM方法中，颗粒参数是基于DEM方法［18］进行求解的。在DEM方法中，支撑剂颗粒被建模为弹性圆球，颗粒之间的作用力通常基于软球模型进行计算。如图1所示（其中，i，j为颗粒编号，δn为重叠量），当圆球之间发生重叠时，认为接触点处存在弹簧和黏壶，二者进行并联后，产生一个综合的作用力。通过这种方式可以考虑颗粒之间的非弹性碰撞。

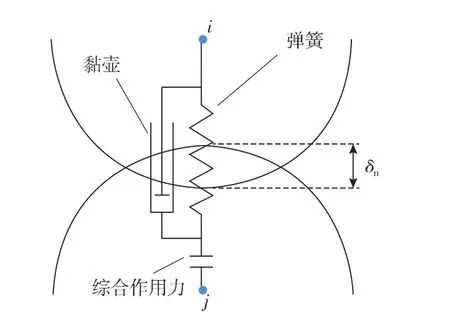
图1 软球模型示意

支撑剂颗粒的运动是基于拉格朗日框架进行描述的，这与描述流体运动的欧拉框架不同，因此CFDDEM方法是一类欧拉-拉格朗日框架混合方法。颗粒的运动遵循牛顿第二定律，可以表述为

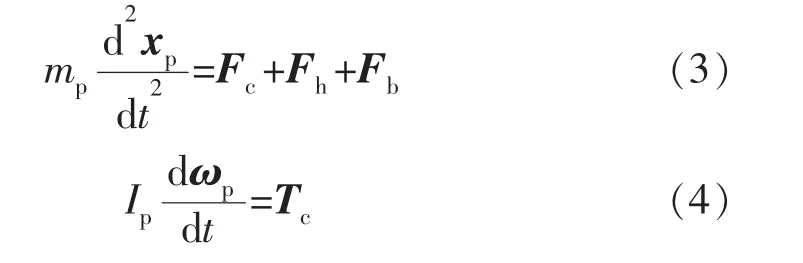
式中：mp为颗粒质量，kg；xp为颗粒位移，m；Fc，Fh，Fb分别为颗粒运动中所受到的颗粒与颗粒/壁面的碰撞力、流体与颗粒耦合的水动力及体积力，N；Ip为颗粒转动惯量，kg·m2；ωp为颗粒角速度，rad/s；Tc为颗粒碰撞过程中产生的力矩，N·m。

式（3）和（4）分别刻画了颗粒的平动方程和转动方程。

1.2 流体与颗粒耦合策略

本文的支撑剂数值模拟是基于开源软件CFDEM实现的［19］，其采取的耦合方法为目前主流的四路耦合策略［20］，这一点从式（1）—（4）也能够得到体现。所谓四路耦合，指的是考虑了流体体积分数对流体控制方程的影响、流体对颗粒的作用、颗粒对流体的反馈作用及颗粒之间的碰撞作用4个方面。

考虑到拖曳力、流体压力梯度力及黏性应力梯度力对水动力的影响，式（3）中的水动力可以表述为

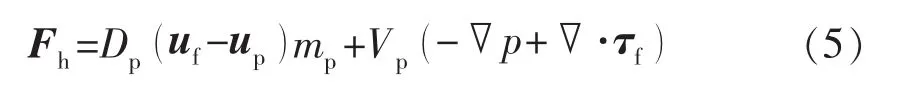
式中：Dp为拖曳力系数，s-1；up为颗粒运动速度，m/s；Vp为颗粒体积，m3。

本文采用Wen&Yu模型计算Dp：

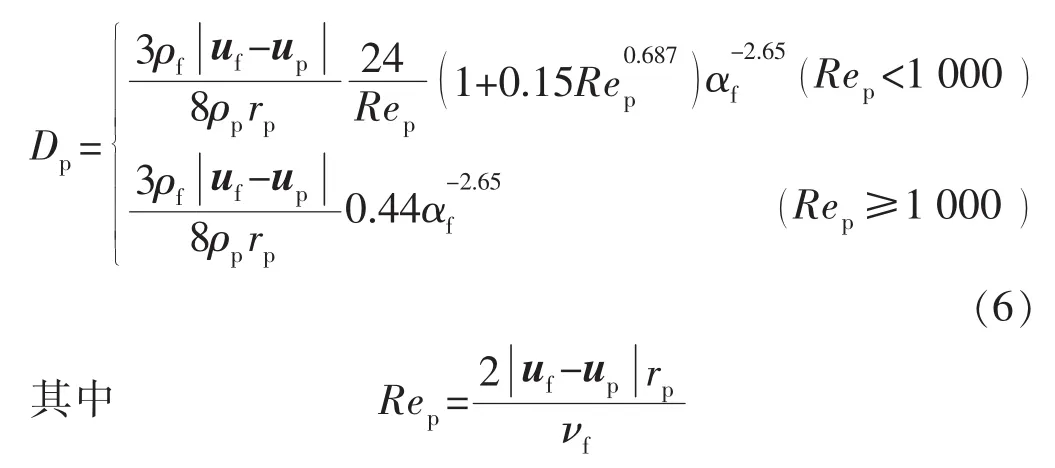
式中：ρp为颗粒密度，kg/m3；rp为颗粒半径，m；Rep为颗粒雷诺数；νf为流体运动黏度，m2/s。

值得注意的是，CFD-DEM方法作为欧拉-拉格朗日混合框架，与常见的双流体模型相比，在具体实现上需要克服混合框架带来的难点。首先，需要利用插值函数完成欧拉网格与拉格朗日点之间的信息交互；其次，流体运动和颗粒碰撞的特征时间是有差别的，流体的计算步长限制通常比颗粒计算步长要大得多。因此，实际耦合过程中，往往采用一步流体计算、多步颗粒计算的显式耦合策略。

1.3 模拟区域及参数设置

本文所模拟的交叉裂缝如图2所示。左侧为携砂液和支撑剂的入口，主流动方向为水平向右，在经过主缝、支缝交叉处时，携砂液及支撑剂发生分流，沿相应的方向流动，直至出口。入口采用定流量的边界条件，出口采用定压的边界条件，具体模拟参数见表1。

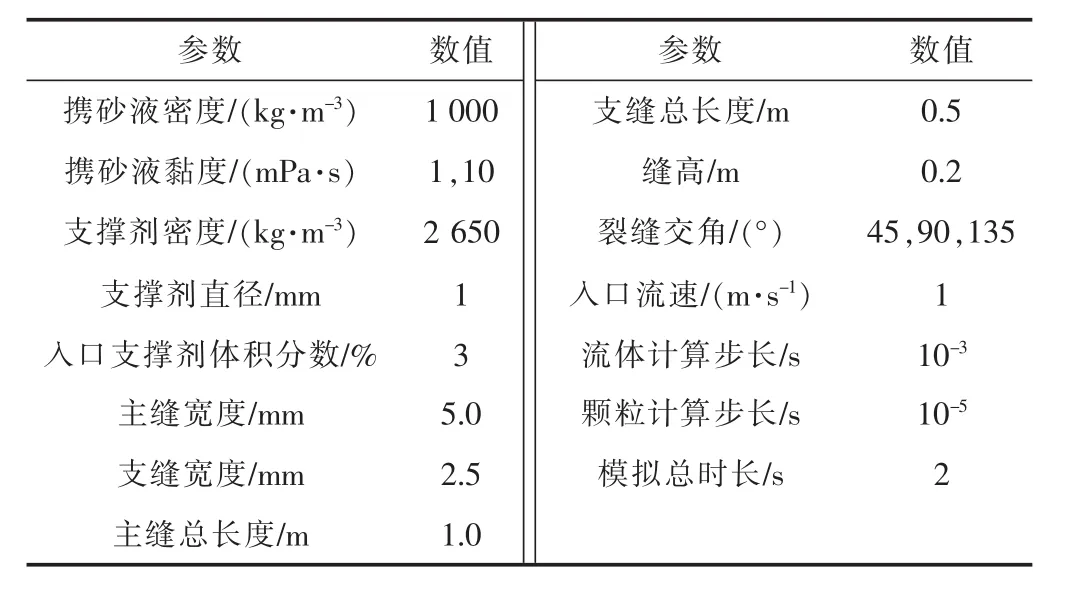
表1 交叉裂缝中支撑剂运移的模拟参数

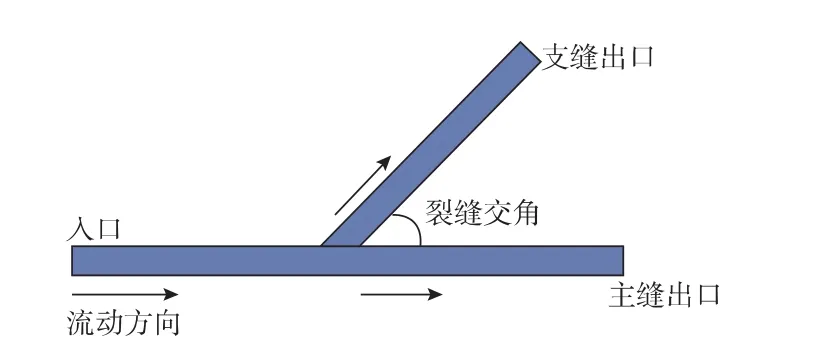
图2 交叉裂缝空间俯视图

在本文算例中，主缝宽度设计为5.0 mm，支缝宽度设计为主缝宽度的一半，即2.5 mm，这主要是考虑到实际情况下支缝宽度通常比主缝小。为了捕捉支撑剂颗粒在裂缝交叉处的运移细节，需要针对流体网格进行局部加密；同时主缝、支缝在远离交叉处的区域，采取逐渐粗化的网格进行模拟，从而降低整体网格数量，进而降低计算量。

2 裂缝交角对支撑剂运移规律的影响

在裂缝交角 θ分别为 45°，90°，135°的条件下，重点考察了支撑剂在携砂液黏度为1 mPa·s时的铺置情况（见图3）。红色区域代表支撑剂高速运移的悬浮区域；蓝色区域的支撑剂颗粒运动速率接近0，可以认为是砂床堆积区域。

图3 低黏条件下支撑剂在不同裂缝交角时的铺置情况

对比图3中的3种情况，可以看出以下运移规律：

1）在携砂液黏度为1 mPa·s的条件下，支撑剂在主缝存在显著沉降。在该算例中，颗粒的沉降速率约为0.134 m/s，因此当不存在颗粒堆积和重力对流作用时，支撑剂的沉降界面（悬浮区域与清水的交界面）斜率接近1/8；而在重力对流的作用下，实际沉降界面斜率明显大于1/8。

2）支撑剂在主缝中的运动速率显著高于支缝。高速流动的红色悬浮区域占主缝前半段的比例明显高于蓝色堆积区域。同时,经过裂缝交叉处后，支撑剂在主缝的后半段发生明显堆积，形成蓝色的静止砂床区域。这是由于在经过裂缝交叉处后，部分流体进入支缝，主缝中的流速骤降，支撑剂在竖直方向上更加容易发生沉降。

3）在不同的裂缝交角条件下，主缝中支撑剂运移状态差异较小，而在支缝中，随着裂缝交角增大，支撑剂进入支缝的比例明显下降。这一效应主要是流体/颗粒的惯性作用导致的。裂缝交角越小，流体/颗粒越容易在惯性作用下进入支缝；而当裂缝交角大于90°时，红色悬浮区域中的支撑剂必须通过在裂缝交叉处发生碰撞、旋转等复杂运动，才能少部分流入支缝当中。

为了定量考察支撑剂在裂缝交叉处的分流规律，分别统计了上述3种情况下支撑剂进入支缝的比例（见表2）。可以看出，在携砂液黏度为1 mPa·s的条件下，随着裂缝交角增大，支撑剂进入支缝的比例是不断下降的。在45°时，支撑剂进入支缝的比例约在1/4；在90°时，支撑剂进入支缝的比例降为1/6左右；在135°时，支撑剂进入支缝的比例降为1/14左右。

表2 支撑剂进入支缝的比例

从图3可以明显看出，在主缝的后半段和支缝中，存在大量蓝色砂床堆积区域。将图3b放大，展示了支撑剂颗粒在裂缝交叉处的堆积细节（见图4）。从图4b可以看出，支撑剂在堆积区域中的排列方式是十分精确、真实的。这表明采用CFD-DEM方法模拟支撑剂运移过程，确实能够捕捉到很多其他数值方法所不能刻画的细节。

图4 裂缝交叉处支撑剂颗粒的堆积细节

3 携砂液黏度对支撑剂运移规律的影响

携砂液黏度为1 mPa·s时，支撑剂在运移过程中有明显堆积行为。这里将携砂液黏度提高至10 mPa·s，进一步考察携砂液黏度对支撑剂在交叉裂缝中运移规律的影响，以及提高携砂液黏度能否提高支撑剂进入支缝的比例。图5展示了携砂液黏度为10 mPa·s条件下支撑剂的铺置情况。同样模拟了3种裂缝交角条件下的情况，与低黏条件下的算例一一对应。支撑剂进入支缝的比例如表2所示。

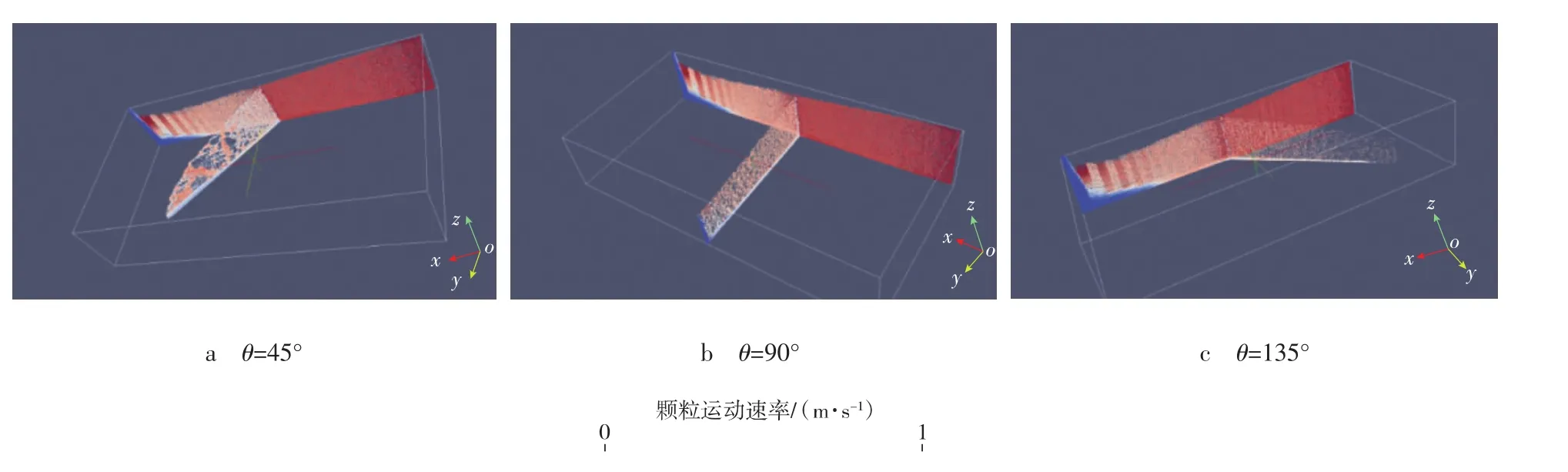
图5 高黏条件下支撑剂在不同裂缝交角时的铺置情况

通过比较图5和图3展示的铺置情况，可以看出提高携砂液黏度后支撑剂运移规律的主要变化。

1）支撑剂在主缝中的水平运移能力明显提高。在提高携砂液黏度后，悬浮区域的沉降界面斜率显著减小。在携砂液黏度为10 mPa·s的条件下，颗粒的沉降速率约为0.052 m/s，约为低黏条件下沉降速率的40%。因此，红色悬浮区域几乎占据主缝前半段的大部分区域，在主缝后半段，颗粒堆积也主要发生在出口附近。

2）支撑剂在支缝中的运移方式发生明显改变，悬浮区域在支缝中的占比明显提高。支撑剂沉降速率的大幅降低，同样有利于它在支缝中的运移。与低黏条件下的运移情况不同，在高黏条件下，主缝悬浮区域中的支撑剂经过裂缝交叉处之后，依然能够整体保持悬浮状态，继续沿支缝方向运移。从定量角度看，高黏条件下支撑剂进入支缝的比例确有明显提高（见表2）。

3）相比于低黏条件，高黏条件下支撑剂在支缝中的宏观运移状态发生明显变化，出现聚团效应。对比图3a与图5a可以发现，在高黏条件下，支缝中悬浮区域内支撑剂的分布更容易演化出空间非均匀性，即聚团效应。细节如图6所示，其中携砂液黏度为10 mPa·s，裂缝交角为45°。从图6可以看出，这种空间非均匀性是在支撑剂进入支缝后不断演化出来的。在靠近交叉处，支撑剂分布的非均匀性结构的尺度很小；而随着支撑剂逐渐向支缝内部运移，这种非均匀性结构的尺度不断加大。这一效应主要是颗粒诱导的流体不稳定造成的。

图6 高黏条件下支撑剂在支缝内运移产生的聚团现象

4 结论

1）随着裂缝交角增大，支撑剂进入支缝的比例不断下降。

2）提高携砂液黏度，能够明显提高支撑剂进入支缝的比例。低黏条件下，支撑剂进入支缝的主要路径是基于悬浮区域分流及砂床迁移机制完成的；而高黏条件下，支撑剂进入支缝的主要路径是通过悬浮区域分流机制完成的。

3）CFD-DEM方法能够精确刻画支撑剂颗粒之间的相互作用，因此可以用于研究砂床堆积的物理机制及运移过程中的聚团效应。

4）本文仅考虑了裂缝交角及携砂液黏度对支撑剂在交叉裂缝中运移规律的影响。事实上，还有许多其他的重要因素及复杂工况尚待研究，包括支撑剂密度、粒径分布、非牛顿流体、复杂缝网等。今后应进一步考察这些情况，揭示相关规律。