车体重心高度和转动惯量对齿轨车辆动力学性能的影响

2021-09-26赵冠闯冯济桥丁军君牛悦丞余浩伟

铁道标准设计 2021年9期

赵冠闯,冯济桥,丁军君,牛悦丞,余浩伟,李艳

(1.西南交通大学机械工程学院,成都 610031； 2.中铁二院工程集团有限公司科学技术研究院,成都 610031)

引言

车体通常由多个模块组成，包括车体钢结构和各种配套设备及零部件等。不同模块的重心位置和转动惯量有所差别，且模块在不同装配位置会对车体重心位置和转动惯量有一定影响[1]。假如将模块分为固定模块和移动模块，固定模块指车体钢结构及吊装在车体上的设备等车辆投入运营后位置固定不变的模块；移动模块则指上下车以及来回走动人员等车辆运行过程中位置发生改变的模块。固定模块的布置决定车体重心位置和转动惯量的主体，移动模块的加入会使得车体重心位置和转动惯量上下浮动，将会直接影响车辆动力学性能，当浮动超过某一范围时则可能引发事故。

针对这一问题，众多学者开展相关研究并取得了一些成果。在2006年、2007年，日本曾经发生运行中的铁道车辆与站台相接触的事故。相关研究表明，主要是由于车体横向振动及车辆运行过程中的加减速等，致使车内站立乘客重心移动从而导致车辆动力学性能超出安全范围[2-3]。LIU等[4]通过对比验证的方式提出一组公式和算法，来计算横风作用下车体重心位置并验证了其准确性；А.Н.КАЖАЕВ等[5]以罐车和漏斗车为实验模型进行实验，探讨了空车重心高度和质量对其安全运行速度的影响，得出漏斗车曲线通过时较为安全的曲线半径及重心在某一变化范围内对动力学性能的影响；雷张文等[6]利用excel软件对车辆的输入参数进行相关计算处理，能够对齿轨车辆进行设备布置优化及调节重心位置；丁军君等[7]利用Simpack软件仿真得到货车重心高度对不同工况下车辆动力学性能的影响。以上研究主要集中在齿轨车辆如何确定或调节重心位置及重心高度对货车的影响，而针对车体重心高度和转动惯量在某一范围内变化对齿轨车辆动力学性能影响的研究较少。

自1812年英国工程师John Blenkinsop构想齿轨铁路开始[8]，国外已有近30个国家开通了180多条各式各样的齿轨铁路，其中，既有作为矿井内运输线路，也有山区观光旅游线路[9-10]。旅游线路中瑞士的皮拉图斯齿轨铁路坡度最大，达480‰，是世界上唯一一条采用Locher模式的齿轨铁路。目前，已有多种不同模式的齿轨线路修建完成并投入使用，且齿轨段运行速度均不大于40 km/h[11-12]，为我国齿轨铁路的修建提供了很好的借鉴作用。

近年来，随着我国轨道交通装备技术的发展及国民对自然风光景点的追捧，国内逐渐对兼具运输和旅游观光的齿轨铁路展开研究。与其他车辆相比，齿轨车辆一般轨距较窄、轴距较大，且为适应乘客观景需求，车体通常以超大玻璃窗为主，车内相关设备与普通列车也有较大差别[13]。同时，由于每个站点、每节车厢所观赏到的景色各有千秋，造成不同站点、不同车厢之间人流量相差较大，致使车体重心高度及转动惯量的变化较大。

以某最高运行速度120 km/h齿轨车辆为例，分析齿轨车辆重心高度及转动惯量变化对其动力学性能产生的影响，为新型齿轨车辆研制提供参考。

1 计算模型

1.1 齿轨车辆动力学模型

以齿轨车辆为研究对象，在多体动力学软件中建立齿轨车辆多刚体系统动力学模型并进行动力学性能仿真计算。该齿轨车辆的主要技术参数为：轨距1 000 mm，轴距2 800 mm，定距11 600 mm，轮直径840 mm，车轮型面为LM型踏面，钢轨质量为50 kg/m。在对车辆运行平稳性仿真过程中考虑侧向风力的影响，即通过仿真得到在有、无侧向风力作用下重心和转动惯量对平稳性的影响趋势。侧向风力在计算时取风压540 N/m2，并忽略车体以下部分所受风力，风力的合力作用于车体侧向投影面积形心上[7]。在有、无侧向风力时均采用车速100 km/h进行仿真，其模型如图1所示。

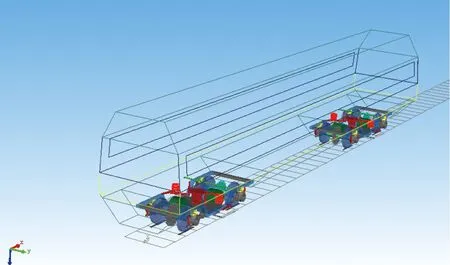
图1 齿轨车辆动力学计算模型

该模型主要由车体和2台性能参数一致的转向架组成，整车系统包括1个车体、2个构架及4组轮对，均将其视为刚体，共计7个刚体[14]。每个刚体有6个自由度，其中，包括伸缩、横移、沉浮、侧滚、点头、摇头，共计需考虑42个自由度，各刚体自由度及车辆拓扑结构如图2所示。

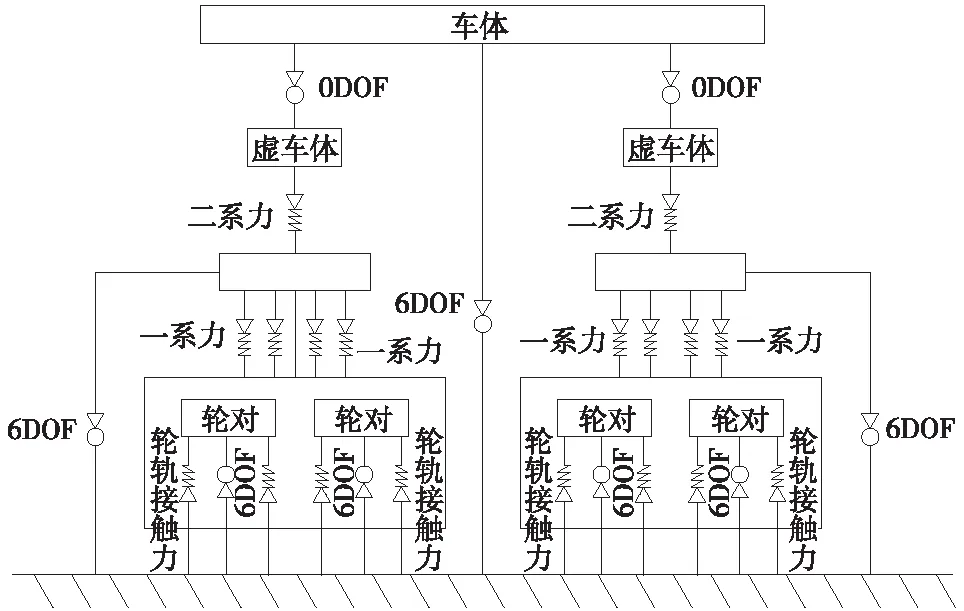
图2 车辆拓扑结构

转向架由轮对、轴箱、构架、基础制动装置、牵引杆、电机齿轮箱及驱动齿轮(仅齿轨车动力转向架有)等组成。转向架定位方式采用转臂式轴箱定位。一系悬挂由钢弹簧、垂向减振器等组成。二系悬挂由空气弹簧、横向减振器、垂向减振器、抗蛇行减振器和抗侧滚扭杆等组成[15-16]。

1.2 重心位置及转动惯量计算方法

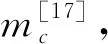
图3 车体重心位置及转动惯量分布示意

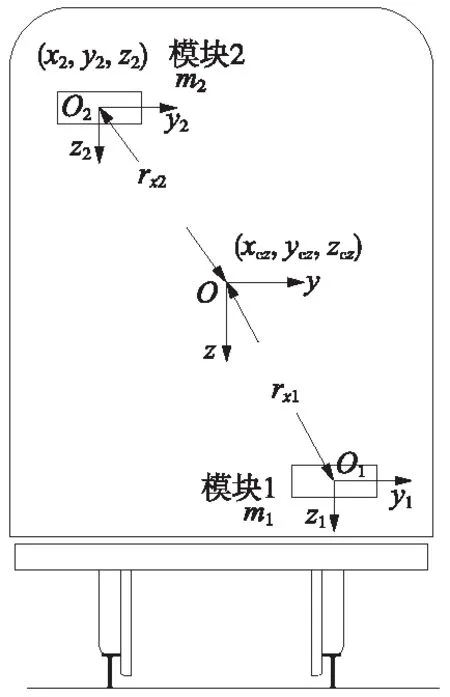
图4 车体重心位置及转动惯量计算示意

(1)

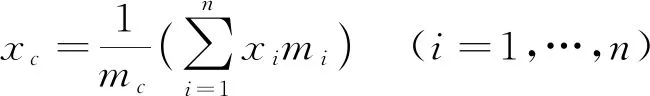
(2)

计算车体转动惯量，以车体钢结构的质心为坐标原点，以图1中的坐标系为基准。因车体是由n个模块组成，即每个模块均有属于其本身的坐标系及绕该坐标系的转动惯量Ixi、Iyi、Izi，如图3所示。以各模块在yoz平面的投影为例绘图，由平行轴定理可得出车体的侧滚、点头、摇头惯量分别为Icx、Icy、Icz，如图4所示。求解过程公式如下

(3)

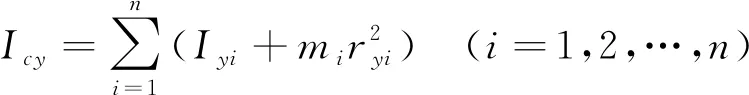
(4)

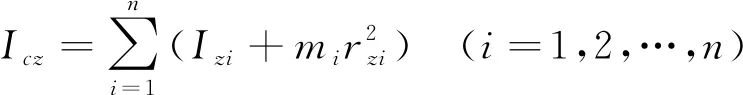
(5)

式中，rxi为第i个模块坐标系中，x轴与车体钢结构坐标系下x轴在yoz平面的投影距离；ryi为第i个模块坐标系中，y轴与车体钢结构坐标系下y轴在xoz平面的投影距离；rzi为第i个模块坐标系中，z轴与车体钢结构坐标系下z轴在xoy平面的投影距离。

通过上述求解方法可得在不同模块数量及不同模块所处位置时的重心高度和转动惯量。因重心高度和转动惯量随车辆设计需求及运行工况发生变化，即文中设定了重心高度和转动惯量变化范围，如表1所示。

表1 变量变化范围

1.3 线路参数设定

在本模型中，对平稳性仿真均为直线路段，对运行安全性仿真均为曲线，曲线线路设置参数如表2所示。

表2 曲线路段线路参数

线路设计完成后，车辆以不同速度通过该曲线，使曲线处于不同的超高状态，其对应速度计算公式为[18]

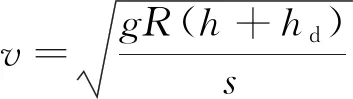
(6)

式中，v为车辆通过速度；s为滚动圆横向跨距；R为曲线半径；h为实设超高值；hd>0即为欠超高；hd<0即为过超高。

为保证车体重心高度和转动惯量变化对运行安全性影响的适用性，选取极限工况下的线路状态分别为欠超高70 mm、过超高50 mm及均衡工况下分析相关影响，对应运行速度分别为100，60，30 km/h。本次仿真不考虑齿轮与齿条的接触关系。

2 动力学性能评价指标

为给相关设计人员提供更好的数据参考，主要通过对车辆临界速度、运行平稳性、运行安全性等方面对该车辆动力学性能进行计算，以此来模拟重心高度、转动惯量等参数对车辆动力学性能的影响。

2.1 临界速度

车辆蛇行运动是由于带有锥度的整体轮对在钢轨上运行而产生的横向振动。对于非线性的车辆系统，蛇行运动的微分方程也是非线性的。齿轨车辆转向架的蛇行运动可采用一个多自由度的整车系统来模拟，其微分方程组的矩阵形式为

(7)

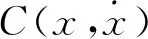
计算机仿真程序中采用数值积分方法求解式(7)。通过观察轮对的横移来判定非线性车辆系统的稳定性。当车辆系统受到一个初始激扰后，通过观察轮对横向振动收敛与发散情况，判断车辆临界速度[7]。

2.2 运行平稳性

根据动力学相关标准规定[19]，客车运行平稳性指标采用下式计算

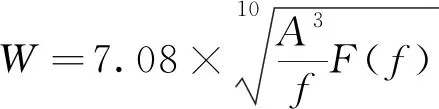
(8)

式中，W为平稳性指标；A为振动加速度；f为振动频率；F(f)为频率修正系数。

2.3 运行安全性

(1)脱轨系数

根据Nadal 公式[20]，脱轨系数评定标准为

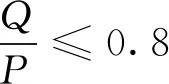
(9)

式中，Q为爬轨侧车轮作用在钢轨上的横向力；P为车轮上的垂向力。

(2)轮重减载率

轮重减载率用于同一轮对上一侧车轮轮重远大于另一侧的条件下，是否会因一侧车轮减载过大而导致脱轨[20]，按以下标准评定

(10)

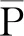
(3)倾覆系数

倾覆系数用于鉴定车辆在侧向风力、离心力、横向振动惯性力同时作用下是否导致车辆倾覆[21]，按以下标准评定

(11)

式中，Pd为车辆同一侧车轮的动载荷；Pst为相应车轮的静载荷。

3 计算结果

3.1 重心高度和转动惯量对车辆平稳性影响

(1)临界速度

车辆临界速度随车体重心高度、转动惯量变化如图5～图7所示。由图5～图7可见，车辆临界速度随车体重心高度增加而减小；随着侧滚、摇头惯量增加整体呈现增大趋势，而点头惯量对临界速度影响较小。

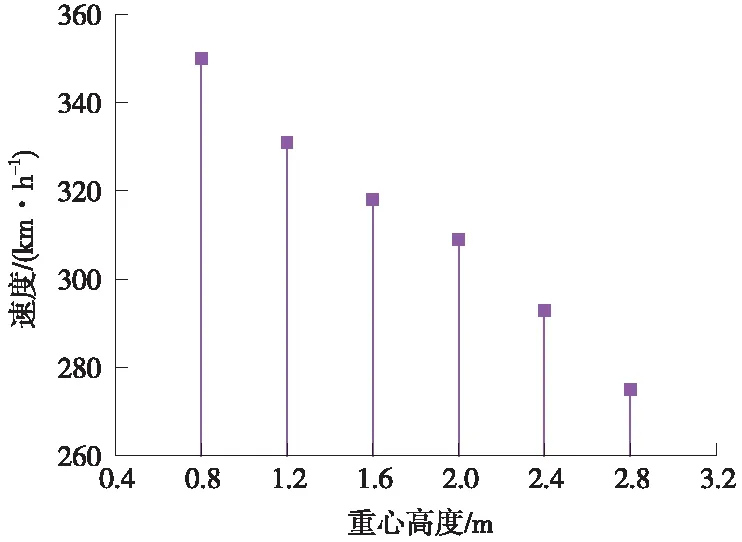
图5 不同车体重心高度的临界速度

图6 不同侧滚惯量的临界速度

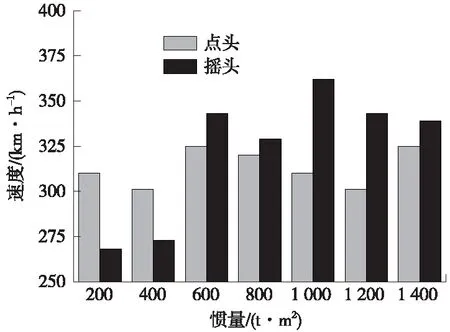
图7 不同点头和摇头惯量的临界速度

(2)平稳性指标

平稳性指标随重心高度、转动惯量变化曲线如图8～图10所示。

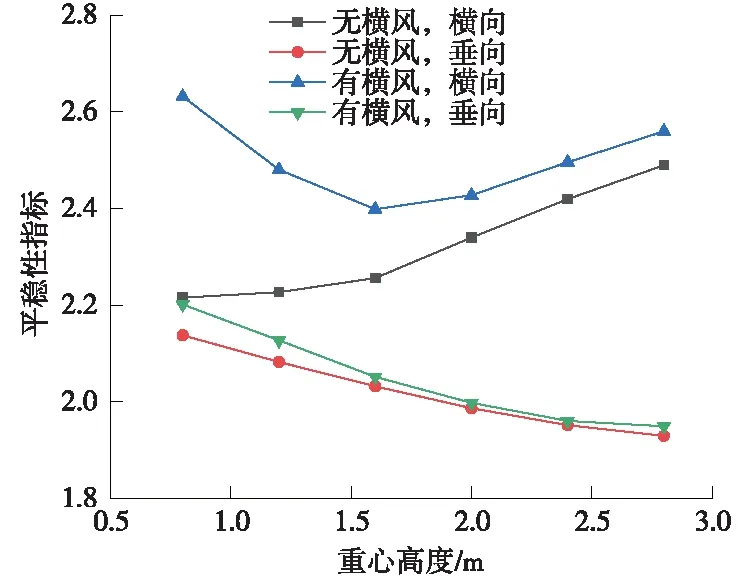
图8 平稳性指标随车体重心高度变化曲线

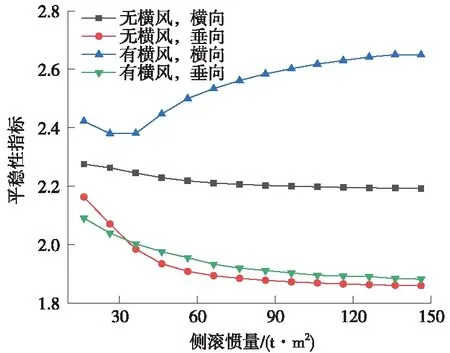
图9 平稳性指标随车体侧滚惯量变化曲线

图10 平稳性指标随车体摇头惯量变化曲线

由图8～图10可见，在有、无侧向风力作用下，垂向平稳性指标随车体重心高度和侧滚惯量的增加整体呈下降趋势。其中，在无侧向风力工况下，随侧滚惯量的增加下降幅度最大，较重心高度0.8m相比总体下降14.02%。

在无侧向风力工况下，横向平稳性指标随摇头惯量的增加整体呈减小趋势，随车体重心高度增加整体呈增大趋势；在有侧向风力工况下，横向平稳性指标随摇头惯量的增加整体呈下降趋势，随车体重心高度的增加整体呈先减小后增大趋势。这是由于当车体重心高度偏离侧向风力合力作用点高度时，会在横向产生作用于车体上的力矩，使横向平稳性指标增大。其中，无侧向风力时，随摇头惯量增加整体变化幅度最大，较重心高度0.8m相比总体下降18.44%。

点头惯量对平稳性指标影响较小，不再赘述。

3.2 车体重心高度和转动惯量对车辆运行安全性影响

3.2.1 车体重心高度对车辆运行安全性影响

(1)轮轨垂向力

轮轨垂向力随车体重心高度变化如图11所示。由图11可见，轮轨垂向力在100，60，30 km/h工况下均随车体重心高度增加整体呈上升趋势。

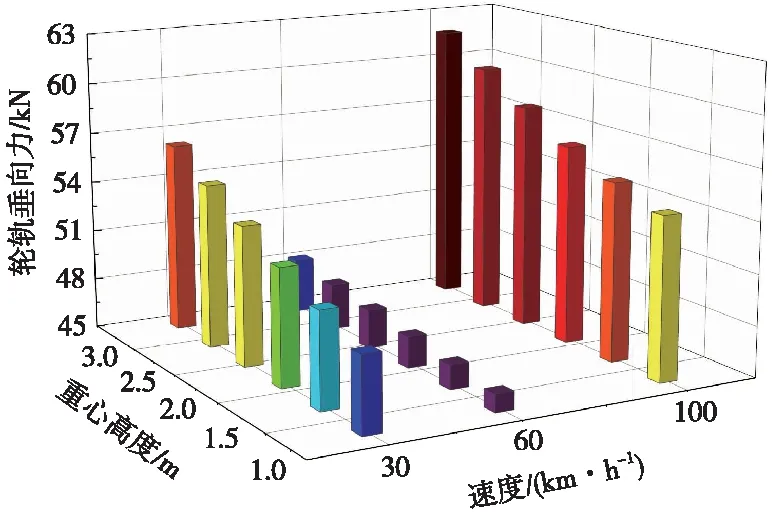
图11 轮轨垂向力随车体重心高度变化

(2)轮轨横向力

轮轨横向力随车体重心高度变化如图12所示。由图12可见，轮轨横向力在100，60，30 km/h工况下均随车体重心高度增加整体呈上升趋势。但在运行速度30 km/h工况下，轮轨横向力大于其他工况，这是由于该工况处于过超高状态产生向心力[18]，与重力分力进行叠加。在运行速度30 km/h工况下，重心高度2.8 m时轮轨横向力达到最大值，较车体重心高度0.8 m相比轮轨横向力增加22.54%。

(3)轮重减载率

轮重减载率随车体重心高度变化如图13所示。由图13可见，轮重减载率在100，60，30 km/h工况下均随车体重心高度增加整体呈上升趋势。

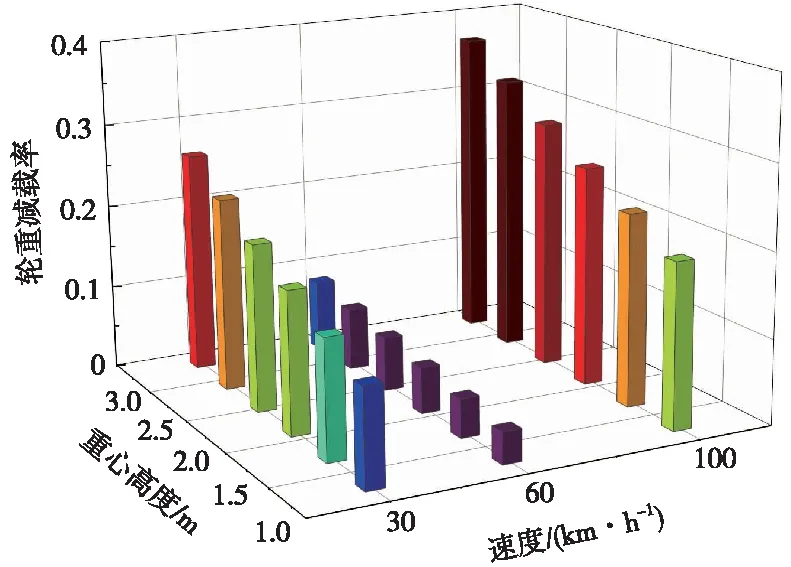
图13 轮重减载率随车体重心高度变化

(4)脱轨系数

脱轨系数随车体重心高度变化如图14所示。由图14可见，脱轨系数在60，30 km/h工况下均随车体重心高度增加整体呈上升趋势，但在100 km/h工况下呈下降趋势。这是由于随重心高度增加，轮轨垂向力和轮轨横向力同时增大，但在100 km/h工况下轮轨横向力增加幅度小于轮轨垂向力增加幅度。脱轨系数由Q/P得来，因此，随重心高度增加脱轨系数呈整体下降趋势。但在100 km/h工况下轮重减载率随重心高度增加而增大，即车辆脱轨危险仍然较大。

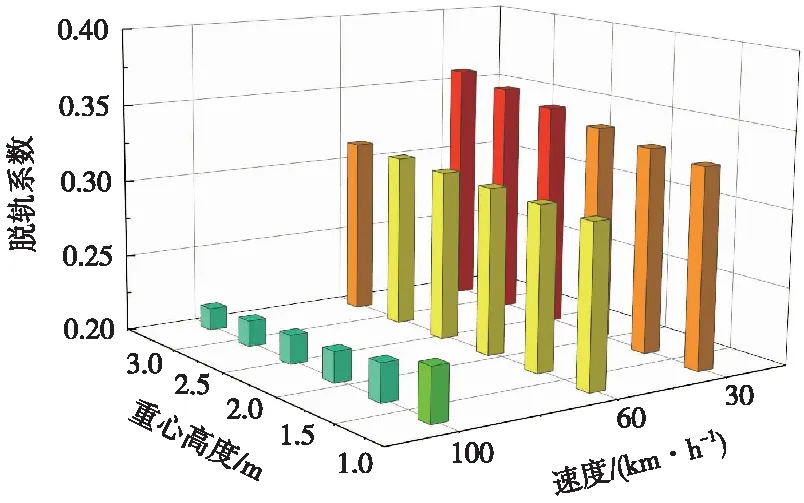
图14 脱轨系数随车体重心高度变化

(5)倾覆系数

倾覆系数随车体重心高度变化如图15所示。由图15可见，倾覆系数在100，60，30 km/h工况下，均随车体重心高度增加整体呈上升趋势，其中，60 km/h工况倾覆系数最小，100 km/h工况倾覆系数最大。这是由于在均衡工况下轮对受力较为均衡，不容易发生倾覆现象。

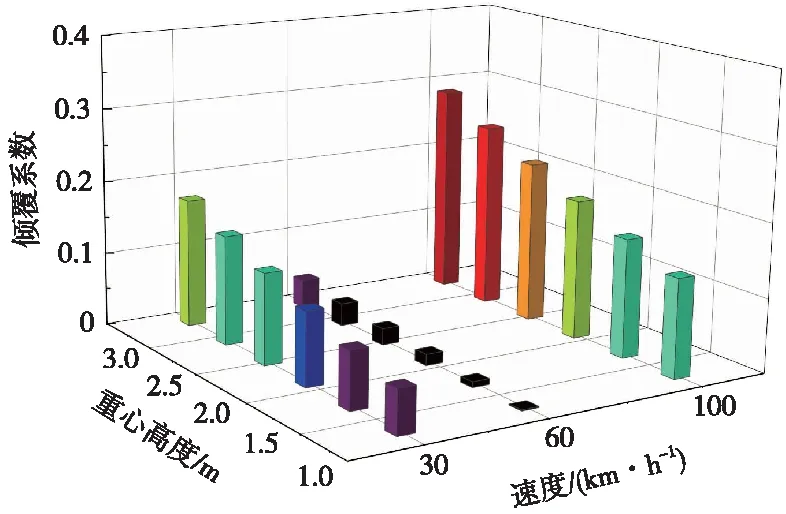
图15 倾覆系数随车体重心高度变化

3.2.2 车体转动惯量对车辆运行安全性指标影响

通过仿真计算，当车体侧滚、摇头、点头惯量发生变化时对车辆运行安全性影响较小，基本可忽略不计。此处以侧滚惯量为例，轮轨垂向力、横向力随侧滚惯量变化如图16、图17所示。

图16 轮轨横向力随侧滚惯量变化

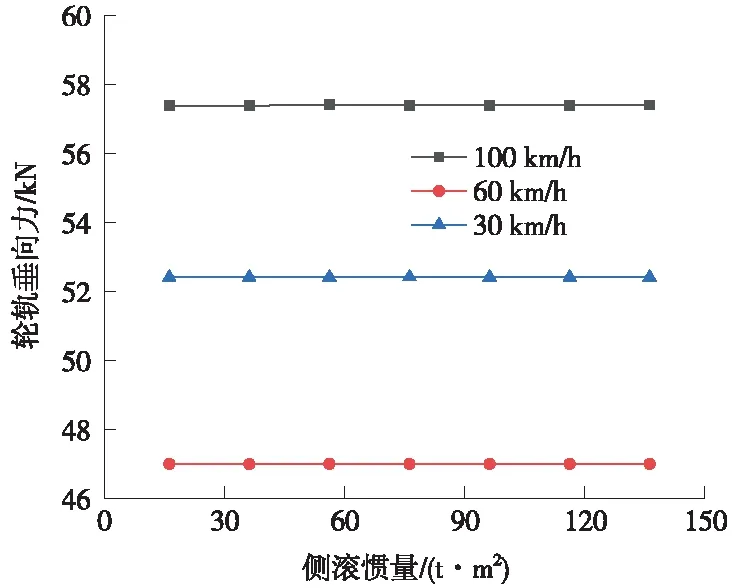
图17 轮轨垂向力随侧滚惯量变化

由图16、图17可见，100，60，30 km/h工况下，轮轨垂向力、横向力变化均较小。图16中轮轨横向力最大值与最小值相差0.0062 kN，较最大值相比总体仅减小0.04%。图17中轮轨垂向力最大值与最小值相差0.021 kN，较大值相比总体仅减小0.04%。综上所述，车体侧滚、摇头、点头惯量变化对车辆运行安全性影响较小，在此不再赘述。