基于改进遗传算法的深度神经网络优化研究*

李 静，莫思敏

(太原科技大学经济与管理学院,山西 太原 030024)

1 引言

人工神经网络ANN(Artificial Neural Network)在人工智能和机器学习领域有着很重要的地位，自1943年提出以来便成为活跃的研究领域[1]。随着大数据时代的到来，深度学习技术不断发展，各种深度神经网络被提出以解决各种问题。然而，神经网络的性能受其结构、超参数影响很大，设计出合理的神经网络结构较为困难，也正因如此，神经网络在很多问题上的应用受到了限制。

近年来，很多专家学者针对神经结构搜索NAS(Neural Architecture Search)进行了一系列研究，旨在设计出一种可以自动搜索出性能最佳的网络结构的技术，这种技术可以根据特定的样本集自动搜索出最优的网络结构。神经结构搜索技术甚至能够搜索出之前人类专家从未发现的网络结构，在某些任务上甚至可能比人类专家水平还要高。

Elsken等人[2]概述了该领域现有研究成果，并从3个维度对它们进行了分类：搜索空间、搜索策略和性能评估策略。搜索策略是指在搜索空间中找到最优网络结构的方法。演化优化作为一种通用的优化方法，已经成功地应用在很多领域中。一些研究表明，针对给定任务，使用演化算法演化神经网络结构参数和超参数往往能够发现有效的神经网络结构。近年来，对神经网络结构优化的研究中出现了很多针对演化算法的研究。Luo等人[3]提出基于连续优化的简单有效的自动神经结构设计方法，解决了在离散空间中搜索神经网络结构效率低下的问题。Liu等人[4]设计了一种基于分层表示方案识别高性能神经结构的演化方法，并将其应用于图像分类领域，显示出了强大的性能。Real等人[5]通过改进演化算法的选择策略自动搜索神经网络结构，开发出了一种图像分类器(AmoebaNet-A)，实验结果显示该图像分类器性能超越了人类专家手工设计的图像分类器。Xie等人[6]使用遗传算法自动搜索深度卷积神经网络结构，取得了不错的实验结果。Han等人[7]针对随机单隐藏层前馈神经网络RSLFN(Random Single-hidden Layer Feedforward neural Network)性能对隐藏神经元的数量和随机初始化的参数高度敏感的问题，使用元启发式优化算法改进RSLFN。Tang等人[8]将动态群优化DGO(Dynamic Group Optimization)算法集成到前馈神经网络中以优化前馈神经网络结构，在收敛速度和避免局部最优方面表现出了良好的性能。文常保等人[9]通过改进遗传算法优化径向基函数神经网络的结构，并根据个体适应度值和迭代次数自适应调整交叉变异概率，增强了算法的局部搜索能力。

刘浩然等人[10]通过改进遗传算法选择策略优化神经网络的权值，并将其应用于水泥回转窑的故障诊断中,验证了算法的可行性。Karaboga等人[11]为避免传统训练算法容易陷入局部最小值和计算复杂的问题，将人工蜂群算法应用于搜寻神经网络的最佳权重集中。Xu等人[12]提出一种改进蜂群优化算法优化前馈人工神经网络的参数，引入了新的选择策略和最佳指导策略。另外，Jaddi等人[13]提出了一种改进的蝙蝠算法和编码方案，结合了基于种群和局部搜索算法的优势以搜索最优网络结构以及ANN权重和偏差,并将其应用于降雨预测问题，得到了令人满意的结果。Heidari等人[14]使用最近提出的蚱蜢优化算法GOA(Grasshopper Optimization Algorithm)提出了一种新的混合随机训练算法，并运用该算法演化ANN的权重及偏差。Xue等人[15]提出了一种基于参数和策略的自适应粒子群优化SPS-PSO(Self-adaptive Parameter and Strategy based Particle Swarm Optimization)算法，通过特征选择来优化前馈神经网络FNN (Feedforward Neural Network)，解决了针对大规模数据集优化权重计算复杂度大的问题。Aljarah等人[16]基于鲸鱼优化算法WOA(Whale Optimization Algorithm)针对神经网络的连接权重进行研究，并且应用改进鲸鱼优化算法训练网络的连接权重，取得了不错的实验结果。

在以上演化算法优化前馈神经网络结构的研究中，一些文献[3 - 9]仅对神经网络的结构进行了优化研究,而另一些文献[10 - 16]则仅对网络连接权重进行优化研究。目前鲜有文献在研究演化算法的同时优化深度前馈神经网络的结构和权重。深度前馈神经网络的结构变量(层和每层节点数量)属于整型变量，而权重属于实数变量，因此，对深度前馈神经网络的结构和权重的优化属于多变量类型优化问题。深度神经网络的权重变量规模之大，亦属于大规模优化问题。为了获得高性能神经网络，本文提出改进遗传算法MGADNN(Modyfied Genetic Algorithm Deep Neural Network)优化深度神经网络,针对变量多类型和大规模优化问题，采用二进制编码与实数编码的混合编码策略对深度前馈神经网络层数、每层节点量以及学习率和权重变量进行编码。并改进遗传算法的选择策略，从父代和子代合并的2n个个体中，选择适应值最高的n/2个个体进入新父代，再根据适应值，以一定的概率选择部分适应值较差的n/2个体进入新父代，以增加种群多样性，避免算法陷入局部最优。同时，引入dropout方法，以减少神经网络过拟合训练数据。利用改进的遗传算法优化神经网络的结构和参数，获得性能较高的神经网络。

2 MGADNN算法

2.1 编码策略

前馈神经网络(FNN)是人工神经网络的一种，采用一种单向多层结构，其中每一层包含若干个神经元。在此种神经网络中，各神经元可以接收前一层神经元的信号，并将计算结果输出到下一层。图1是一个2层前馈神经网络结构。

Figure 1 Structure of neural network 图1 神经网络结构图

网络中每个节点的输出分2步计算。 首先，使用式(1)计算隐藏层中第j个节点的输出：

(1)

其中，第1项为输入的加权总和，n表示输入数量，Ii表示第i个输入变量，wkij表示第k层Ii与隐藏层神经元Hj之间的连接权重。例如，w111表示输入层第1个节点到隐藏层第1个节点的连接权重。第2项βj为偏置项。其次，使用激活函数来触发神经元的输出。FNN中可以使用不同类型的激活功能。本文使用文献中应用最广泛的S形函数[12]，如式(2)所示：

(2)

因此，可以通过式(3)获得神经元的输出:

(3)

神经网络中常用的损失函数有回归损失函数、平方误差损失函数和绝对误差损失函数等，本文使用平方误差损失函数作为训练过程中的损失函数。

通过设计的人工神经网络结构来训练数据以更新网络的权重。通过不断训练网络模型更新权重以达到使误差最小化的目标。神经网络的训练过程是一项具有挑战性的任务，可以提高人工神经网络解决各种问题的能力。

本文需要优化的参数有网络结构(即网络层数和每层的节点量)、权重、学习率和采用二进制编码和实数编码方式。其中，针对网络结构优化采用二进制编码，对权重和学习率采用实数编码。

例如图1所示的2层神经网络结构，该神经网络模型用来训练具有2个特征的二分类数据，其中输入层到隐藏层之间的连接权重为第1层的连接权重。图1所示的神经网络结构(层数、节点量)的二进制编码方式如图2所示：前3位表示层数，010表示这是一个2层神经网络结构，后5位表示层节点量，第1层节点量二进制编码00011表示第1层有3个节点，第2层节点量00010表示第2层有2个节点。层与层之间连接权重的编码如图3所示，按照顺序存放在矩阵中。针对学习率的编码如图4所示，其中Lr1表示第1个模型的学习率。

Figure 2 Encoding of number of network layers and number of nodes in each layer 图2 网络层数及每层节点量编码

Figure 3 Weight encoding图3 权重编码

Figure 4 Learning rate encoding图4 学习率编码

2.2 MGADNN算法的选择策略

遗传算法是受达尔文进化论的启发，借鉴生物进化过程而提出的一种启发式搜索算法。算法通过选择、交叉和变异等机制搜索解空间的优秀个体。选择操作对遗传算法性能影响很大，常见的选择策略有轮盘赌选择法、精英选择法等，其中轮盘赌选择法是首先根据个体适应值计算概率，然后根据这个概率随机选择个体，它的本质是适应值好的个体被选中的几率更大，没有考虑所选择个体构成种群的多样性。精英选择法是将子代和父代中的个体按照适应值排名，然后选择适应值最好的个体构成种群。这种选择策略仅选择适应值好的个体，显然会造成种群多样性差，易陷入局部最优的问题。刘浩然等人[10]改进了遗传算法的选择策略，将种群中的个体按照适应值从差到优排序后平均分为3部分，并设置这3部分被选择个体的概率为0.6,0.8,1，以达到多选适应值好的个体，少选适应值差的个体的目的，这种方法在一定程度上引进了适应值差的个体，有利于避免算法陷入局部最优。选择概率是针对水泥回转窑数据人工设定的经验值。对于基于其他训练数据的神经网络优化，这种选择策略可能未必有效。对于优化神经网络这样复杂问题，需要遗传算法具有较好的多样性，而固定概率值的选择策略可能会使算法的多样性受到影响，不利于寻找到性能较高的神经网络。

因此，本文改进了遗传算法的选择策略，该算法的思路是根据个体的适应值，构建一个以个体适应值为变量的概率函数，以一定的概率选择适应值较差的个体并与适应值较好的个体混合构成新父代。算法步骤如下所示：

(1)将子代个体与父代个体合并，假设种群规模为n，合并子代与父代后个体数量为2n；

(2)将合并后群体中的2n个个体依据其目标函数值(本文以神经网络在训练数据上的平方误差值MSE为目标函数值，MSE值越小，网络性能越好，个体目标函数值越小，个体适应值越好)从小到大排列，目标函数值小的个体其排名值也小；

(3)将排序后的个体分为2段，前n/2个个体为第1段，后3n/2个体为第2段；

(4)前n/2个个体被直接保留为新父代的一部分个体，根据式(4)从第2段3n/2个个体中，概率选择n/2个个体，形成新父代的剩余部分。

(4)

其中，p(j)表示第j个个体被选中的概率，r(j)表示第j个个体按照目标函数值从小到大排序在整体中的排名值。目标函数值小的个体其排名值也小，目标函数值大的个体其排名值也大。

下面用种群数为6并标有个体标号以及目标函数值的种群为例，使用图形描述上述思想。

(1)设种群规模为6，即n=6，则父代和子代种群个体混合组成一个个体数为12的种群：

其中，fi表示第i个个体的适应值，例如f1=5表示第1个个体的适应值为5，f2=8表示第2个个体的适应值为8。

(2)将12个个体按照目标函数值从小到大排序：

(3)将排序后的个体分为2段，前n/2个个体为第1段，后3n/2个体为第2段：

2.3 MGADNN算法的收敛性和多样性分析

按照改进的选择策略,算法在每一演化代t，混合父代与子代个体，形成包含2n个个体的群体，按照适应值对此群个体排序，并从中选择适应值最好的n/2个个体作为新父代的一部分(记为A1(t))，再从其余3n/2个个体中依据个体适应值，概率地选择适应值较差的n/2个体(记为A2(t))。新父代P(t+1)=A1(t)∪A2(t)。假设到第t代时，I*(t) 为P(t) 种群中的最优个体。根据本文的选择策略，构成新父代群体P(t+1)的A1(t)中包含适应值等于或优于I*(t)的个体。因此，在整个演化过程中，历史发现的精英个体始终被保留在种群中。理论已经证明精英保留的标准遗传算法是全局收敛的[17]。在本文的改进算法中，精英个体被保留在种群中，对算法的全局收敛能力产生了较大作用。

在构成父代群体P(t+1)的A2(t)中包含部分适应值较差的个体，增加了群体多样性，有利于算法跳出局部最优，进而能够发现性能更好的神经网络。因为，在A1(t)和A2(t)中个体数量相等，所以能够兼顾算法的收敛性和多样性。

2.4 MGADNN算法对神经网络性能的影响

在本文中，神经网络在训练过程中采用后向传播BP(Back Propagation)算法优化权重。BP算法是从解空间一点上按照梯度下降的方法开始搜索的确定性算法。因此，初始值和学习率对BP算法性能影响较大，不合适的初始值将导致搜索陷入局部最优。初始值的设置对搜索到较高性能的神经网络有重要影响。遗传算法的全局搜索能力较强，本文设计的选择策略相较于精英选择策略，增加了种群的多样性，提高了算法在全局范围内搜索最优解的能力。因此，本文在每一个演化代，首先使用改进遗传算法优化神经网络权重，以寻找合适的初始值。之后，在神经网络训练阶段，BP算法基于此初始值开始网络训练。

2.5 MGADNN算法流程

MGADNN算法的基本思想是：将FNN结构(网络层数、每层的节点量)进行二进制编码，学习率及网络权重使用实数编码，随机初始化后输入改进遗传算法中演化，将前馈神经网络的预测误差作为该个体的目标函数值，通过选择、交叉和变异等遗传操作寻找最优个体，即最优的前馈神经网络结构、学习率和权重，直到满足实验设置的最大迭代次数结束。

(1)种群初始化，根据各个体构建神经网络模型，t=0;

(2)在第t代，父代P(t) 执行随机单点交叉变异操作，产生新的子代个体Q′(t);

(3)BP算法训练每个子代个体Q′(t)(神经网络)获得学习后的子代Q(t)，将子代的权重值作为神经网络训练阶段BP算法优化的权重初始值;

(4)依据式(5)计算子代Q(t)个体的目标函数值;

(5)将父代P(t)与子代Q(t)个体合并，依据2.2节改进的选择策略选择个体组成新父代P(t+1);

(6)当达到种群最大迭代次数，则停止优化，进入步骤(7)，否则t=t+1，返回步骤(2);

(7)种群个体(神经网络)对测试数据进行预测，获得测试误差值最小的神经网络。

3 dropout方法

深度神经网络具有强大的学习能力，但是过拟合问题是此类网络的一个严重问题，并且过于复杂的深度神经网络消耗大量存储空间和计算资源。dropout方法[18]是针对这个问题被提出的。dropout是一种正则化方法，它主要通过随机删除网络中的神经元和神经元连接的边以得到一个更加精简的网络。dropout方法工作原理如图5所示，图5a表示没有使用dropout方法的全连接网络，使用dropout方法后，首先遍历网络中的每一层，并根据设置的节点保留概率和删除概率，随机删除一些节点，然后删除掉与该节点相关的边，最终得到一个节点更少、结构更简单的网络，如图5b所示。

Figure 5 Diagrams of the full connection network and using of dropout network 图5 全连接网络与使用dropout网络结构图

假设设置dropout方法随机删除节点的概率为0.5，即每个节点被保留和删除的概率均为0.5，dropout方法随机遍历网络后按照0.5的概率随机删除部分节点以及与该节点相关的边，图5b为精简后的网络结构。从图5可以很直观地看出，使用dropout方法后网络随机去掉了一些节点和边，使得网络更加简单。

4 目标函数

为了与其他相关文献的实验结果进行比较，本文以均方误差MSE(Mean-Square Error)作为目标函数，如式(5)表示：

(5)

5 实验与结果分析

5.1 实验数据

表1为实验所用数据集的基本信息。如表1所示，本文所选数据集具有不同数量的特征和样本，以在不同条件下测试算法，使得实验结果更具说服力。实验设置如表2所示。

Table 1 Experimental datasets表1 实验数据集

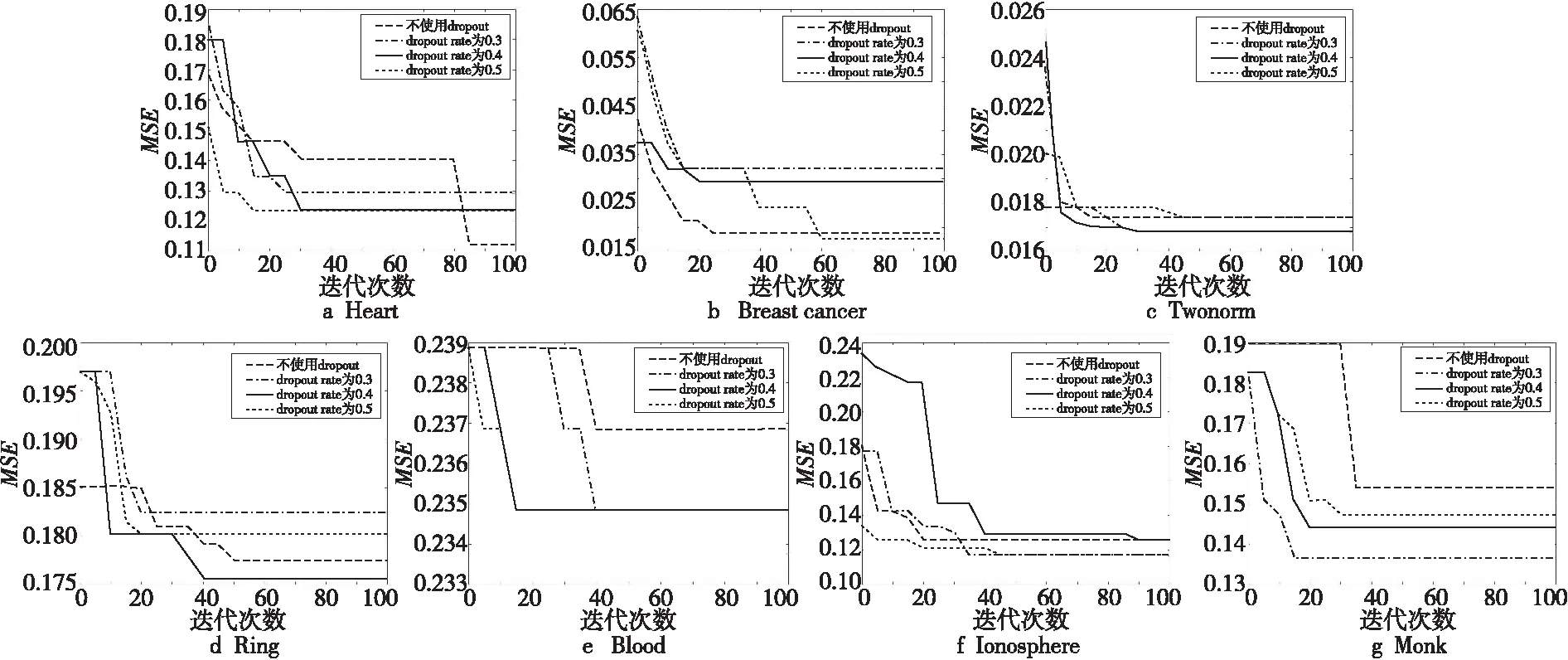
Figure 6 Influence of dropout method on experiment results图6 dropout方法对实验结果的影响

Table 2 MGADNN algorithm parameter setting

通过研究文献发现，深层神经网络结构训练数据在一定的范围内网络结构越复杂其结果越好，但超过这个范围，太深层的网络结构反而会出现过拟合现象，导致网络性能下降。所以，本文将待优化的网络层数最大值设置为7层，每层的节点数量最大值设置为31。利用二进制编码，则前3位表示网络层数，后5位表示每层节点数量。

5.2 dropout方法对实验结果影响

本节研究dropout方法在不同的随机删点的概率下对实验结果的影响。分别设置dropout率为0.2,0.3,0.4,0.5作为实验条件，并使用具有不同特征数量、不同数据量的Heart、Breast cancer、Twonorm、Ring、Blood、Ionosphere、Monk数据集进行数值实验,使用本文改进算法独立运行并且采用分类准确度Accuracy作为评价指标。

图6是每代种群中最优值(每一代最小MSE值)的演化曲线图，表3则是演化结束后种群个体在测试数据集上的最好值(Accuracy最大值)。由表3可以看出，Heart数据集和Breast cancer数据集在实验设置dropout率为0.4和0.5实验条件下的分类准确度最好，Twonorm数据集和Ring数据集在实验设置dropout率为0.4条件下实验结果最好。由图6a在训练数据上的收敛曲线并结合表3测试数据分类准确度可以看出，在Heart数据集上训练不使用dropout方法时，收敛效果更好，但是从表3分类结果可以看出，虽然训练过程中MSE最终降到了最低，但是其测试数据的分类准确度却是最差的，由此可以看出存在过拟合现象。如图6e所示，在Blood数据集上dropout率为0.4时，训练过程中的MSE降到了最低，并且在测试数据上的分类准确度最高。图6f所示，Ionosphere数据集在训练过程中，当dropout率为0.3和0.5时，MSE降到了最低，如表3所示，当设置dropout率为0.3时，其演化结束后种群个体在测试数据上的分类准确度最高。如图6g所示，针对Monk数据集，当设置dropout率为0.3时，在训练过程中其MSE降到了最低，但是最好的测试数据实验结果出现在dropout率为0.4和dropout率为0.5的条件下。针对每一个数据集，在测试数据上最好的实验结果总是在使用dropout方法时出现，由此可以看出dropout方法在避免数据过拟合方面起了很大作用。

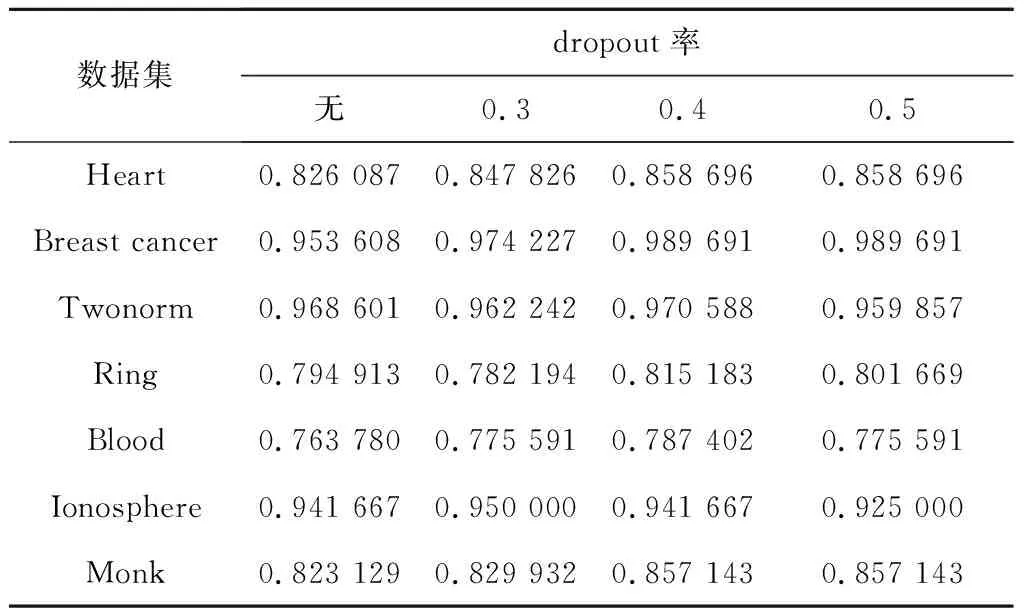
Table 3 Influence of dropout on Accuracy表3 dropout对分类准确度Accuracy的影响

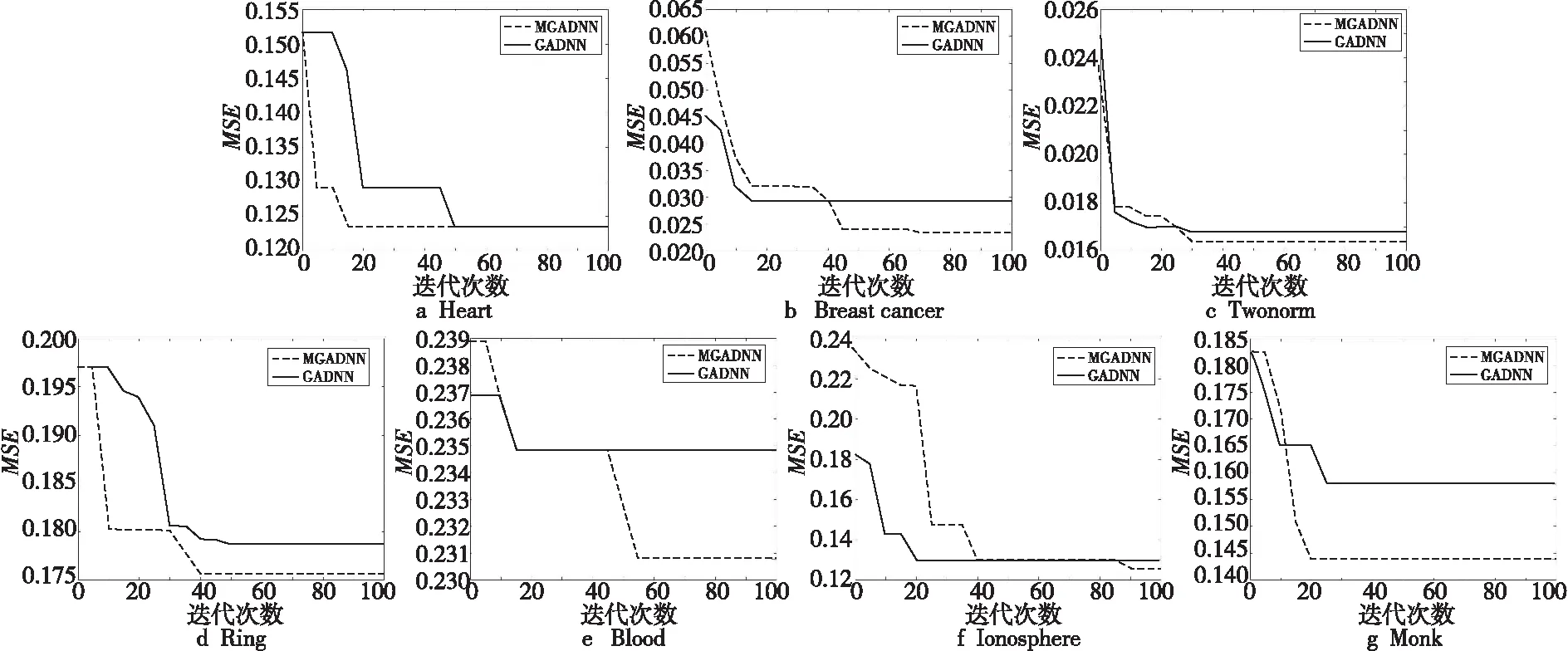
Figure 7 Experimental results of MGADNN algorithm and GADNN algorithm图7 MGADNN算法与GADNN算法实验结果

5.3 MGADNN实验结果

为了尽可能保留样本分布，将所有数据集中数据的66%用于训练，34%用于测试。 此外，为消除具有不同数值范围特征的影响，所有数据均使用最小-最大归一化进行归一化，如式(6)所示：

(6)

其中，v′∈(minA,maxA)表示数据v的归一化结果。为了将实验结果与其他算法进行比较，本文采用与文献[16]相同的实验设置，使用Heart、Breast cancer、Twonorm、Ring、Blood、Ionosphere、Monk数据集作为实验数据，以分类准确度Accuracy作为评价指标。

表4所示为演化结束后种群个体在测试数据上的最好值(Accuracy最大值)，结果表明针对Heart、Breast cancer、Twonorm、Ring、Blood、Ionosphere和Monk数据集，MGADNN算法较遗传算法优化深度神经网络算法(GADNN)测试分类准确度更高。结合图7a每代种群中最优值(每一代最小MSE值)的演化曲线图可以看出，使用2种算法训练Heart数据集，训练过程中2种算法的MSE最终都降到了相同水平，但是测试数据的分类准确度表明MGADNN算法性能更好，说明MGADNN搜索到的网络在训练数据和测试数据上都能获得好的性能。针对Breast cancer、Twonorm、Ring、Blood、Ionosphere、Monk数据集，从实验结果即测试数据的分类准确度Accuracy可以看出，MGADNN算法在测试数据上的分类准确度总是最高；从训练过程中的收敛曲线可以看出，MGADNN算法训练数据收敛速度较快。综上所述，与GADNN算法相比较，MGADNN算法能够搜索到性能更佳的网络。

结合图7每代种群中最优值(每一代最小MSE值)的演化曲线图可以看出，MGADNN算法的演化曲线收敛速度最快，并且MSE值总是降到最低，结合表4中MGADNN算法在测试数据集上的分类准确度总是最高，表明该算法训练出的网络性能各方面都优于GADNN算法的。

Table 4 Experimental results of MGADNN and GADNN (Accuracy as an evaluation index)表4 MGADNN与GADNN实验结果(Accuracy作为评价指标)

5.4 与相关文献结果比较

本文使用的实验设置同文献[16]，使用Breast cancer、Ring和Twonorm、Blood、Ionosphere和Monk数据集进行实验，将实验最好结果与参考文献[16]中的其他算法进行对比，对比结果如表5所示。

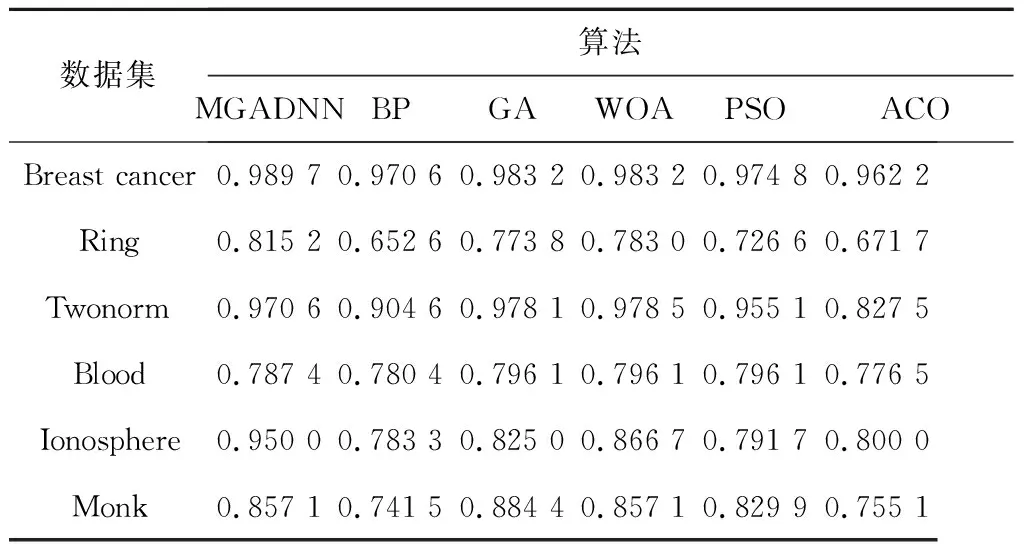
Table 5 Experimental results comparison of various algorithms (Accuracy as an evaluation index)表5 各算法实验结果比较(Accuracy作为评价指标)

文献[16]中提到鲸鱼优化算法WOA(Whale Optimization Algorithm)及其对比的BP、GA、PSO、ACO算法都仅仅是优化了前馈神经网络的连接权重，并没有对神经网络的结构(比如网络层数、每层神经元个数)进行优化。实验结果显示，本文提出的MGADNN算法在Breast cancer、Ring和Ionosphere数据集上性能优于BP、GA、WOA、PSO和ACO算法的；在Twonorm数据集上的性能优于BP、PSO和ACO算法的；在Blood数据集上，本文提出的MGADNN算法的分类准确度优于BP算法和ACO算法的，但是比GA、WOA和PSO算法的差；在Monk数据集上，分类准确度最高的算法为GA算法，本文提出的算法优于BP、PSO和ACO算法。

6 结束语

本文通过改进的遗传算法优化深度前馈神经网络的结构和超参数，自动设计出适合不同数据的最优网络结构。本文使用Ring、Breast cancer、 Twonorm、Heart、Blood、Ionosphere和Monk数据集进行数值实验，验证了dropout方法可以有效避免过拟合，故将dropout方法应用到本文所提算法中。同时，在相同dropout率条件下对比MGADNN算法与GADNN算法，实验结果表明，MGADNN算法由于改进了遗传算法选择策略，以一定概率引入一些适应值较差的个体，增加了群体多样性。在相同的实验条件下，与其他文献作比较，仿真结果表明，本文设计的算法够搜索到性能更佳的神经网络。

本文通过dropout方法随机从神经网络中删除一些节点来避免神经网络过拟合训练数据，效果明显，但针对不同的数据需要寻找合适的dropout率，因此设计适应不同数据的新剪枝方法并将其与演化算法结合去寻找性能更佳的神经网络需要进一步研究。