求解带容量和时间窗约束车辆路径问题的改进蝙蝠算法*
2021-09-24戴二壮
张 瑾,洪 莉,戴二壮
(河南大学计算机与信息工程学院,河南 开封 475004)
1 引言
车辆路径问题VRP(Vehicle Routing Problem)是物流理论体系中一类经典的组合优化问题,随着物流业的不断发展,越来越多的VRP问题模型得以产生和发展,如带容量约束的VRP CVRP(Capacitated VRP)、带时间窗约束的VRP VRPTW(VRP with Time Windows)以及带容量和时间窗约束的VRP CVRPTW(Capacitated VRP with Time Windows)[1]等。
由于上述问题都属于NP难题,对于较大规模问题,精确算法难以在有限时间内给出最优解,因此普遍采用智能算法进行求解。现有关于CVRPTW问题的算法大致有遗传算法GA(Genetic Algorithm)、蚁群算法、禁忌搜索算法、粒子群优化PSO(Particle Swarm Optimization)算法、蝙蝠算法和狼群算法等,问题的优化目标大多为运输距离最短或时间最短,部分文献考虑了违反时间窗约束的惩罚成本。采用遗传算法GA求解的文献中,Jiang等[2]通过合理构造染色体,利用遗传算法使最优解的搜索在可行空间内进行;赵振华等[3]提出一种先考虑客户服务的先后次序,然后在此基础上构建初始种群的方法,二者都以运距最短为优化目标;李加玲等[4]在遗传算法中引入轮盘赌策略寻找可行的配送路径;黄务兰等[5]引入精英保留策略,采用客户点交叉和路段交叉算子相结合的方式以保证算法中种群的多样性,二者都以配送时间最短作为优化目标。采用蚁群算法求解的文献中,李琳等[6]在算法的不同阶段采用不同的信息素挥发策略防止算法陷入局部最优;辜勇等[7]以改进蚁群算法为主体,插入遗传操作算子作为局部优化方法,二者都以运距最短为优化目标;黄震等[8]在节点选择概率公式中引入时间窗因素来初始化种群,然后引入遗传操作的交叉和变异算子对路径进行优化;李奕颖等[9]采用改进的状态转移规则和轮盘赌选择机制构建初始解,并结合k元素优化k-opt(k-optimization)邻域搜索进行优化,二者都以配送车辆最少和运距最短为优化目标。采用禁忌搜索算法求解的文献中,钟石泉等[10]引入多初始解和全局禁忌表等措施,旨在扩大搜索范围并减少解的不稳定性,以运距和违反时间窗约束的惩罚成本之和最小为优化目标;Chen等[11]在禁忌搜索算法中引入遗传操作算子进行初始化,并采用2-opt操作进行局部优化;李明燏等[12]引入一条虚拟的路径作为保留表,已选择路径上的用户点可以与保留表中的用户点进行交换和移动,以便扩大搜索空间,二者都以运距最短为优化目标。采用粒子群优化算法PSO求解的文献中,李宁等[13]在初始化时将粒子群划分为若干个两两重叠的相邻子群,使算法跳出局部最优;马炫等[14]提出一种基于粒子交换原理的整数粒子更新方法;罗耀[15]引入微生物行为机制中的趋化、繁殖和迁移算子对算法进行优化,三者都以总运距和违反时间窗约束的惩罚成本之和最小为优化目标;王飞[16]在惯性权重递减的基础上通过群体极值进行t分布变异,使算法跳出局部最优;Marinakis等[17]提出一种多自适应粒子群优化算法,二者都以最短运距为优化目标。采用蝙蝠算法求解的文献中,马祥丽等[18]针对带时间窗车辆路径问题的具体特征对蝙蝠算法的操作算子进行重新设计,以运距最短为优化目标;戚远航等[19]以硬时间窗为约束条件(即车辆在客户时间窗之外到达不进行配送,反之则为软时间窗约束),引入随机插入搜索、最少客户车辆插入搜索、普通插入搜索和交换搜索等策略来扩大搜索空间,以配送车辆最少和运距最短为优化目标;孙奇等[20]加入贪婪随机自适应启发式策略提高求解精度,引入病毒进化机制使蝙蝠算法跳出局部最优,以客户满意度最大和运距最短为优化目标。采用狼群算法求解的文献中,叶勇等[21]利用近邻初始化方式构建初始解,结合狼群算法觅食行为中的游走、召唤和围攻3种行为重新定义其智能行为,以运距最短为优化目标。
上述文献在求解CVRPTW问题时均取得了一定的成果,但其多考虑硬时间窗约束,目标函数大多以运输距离或时间最短为优化目标,且采用的测试案例基本都是小规模的,未涉及较大规模问题的求解。由于在实际物流运输中软时间窗约束更符合客户需求,本文将综合考虑包含车辆使用成本、运输成本和违反时间窗约束的惩罚成本在内的带软时间窗和容量约束的车辆路径问题。蝙蝠算法是一种较为新颖的智能优化算法,在离散优化领域应用较少,为了提高CVRPTW问题的求解精度,本文设计了一种改进的离散蝙蝠算法DBA(Discrete Bat Algorithm),并考虑了较大规模问题的有效求解。
2 求解问题描述
本文研究的问题为:在同时满足客户软时间窗约束和车载容量约束的前提下,通过合理安排车辆配送路线,使得包含车辆使用成本、运输成本和违反时间窗约束的惩罚成本最小。问题研究的前提条件如下所示:
(1)配送起点和终点唯一;
(2)所有车辆容量相同,每个客户点仅由1辆车提供服务;
(3)每个客户点的需求量已知,时间窗约束唯一,无优先服务约束。
模型中相关重要参数定义如下所示:
Z:总成本;
N:客户点总量;
Q:车辆的最大载重量;
c:单位车辆的固定费用;
b:单位距离油耗成本;
dij:客户点i到客户点j之间的距离;
Ai:车辆到达客户点i的时间点;
ti:为客户点i进行服务所需时间;
qi:客户点i的货物重量;
Sj:客户点j的时间窗开始点;
Ej:客户点j的时间窗结束点;
e:早于客户最早时间窗到达的惩罚系数;
l:晚于客户最晚时间窗到达的惩罚系数;
tij:车辆从客户点i到客户点j的运行时间;
S:客户点的编号集合,S⊆{1,2,…,N};
x0jk:表示车辆k从配送中心驶向客户点j;
xi0k:表示车辆k从客户点i返回配送中心。
决策变量为:
K:所需车辆总数;
xijk:0-1变量,当车辆k由客户点i到达客户点j时为1,否则为0;
yik:0-1变量,当车辆k为客户点i提供服务时为1,否则为0。
构建模型如式(1)~式(11)所示,其中式(1)为目标函数,表示包含车辆租赁成本、违反时间窗约束的惩罚成本以及与行驶距离相关的油耗成本在内的总配送成本最小;式(2)表示每辆车装载的货物总量不超过车辆的最大容量;式(3)表示每个客户点由且仅由1辆车提供服务;式(4)保证客户点j之前的临近节点只有1个;式(5)保证客户点i之后的临近节点只有1个;式(6)表示从配送中心出发的车辆在完成配送任务后要返回配送中心;式(7)表示消除子回路即消除车辆不是从车场出发的现象,式(4)~式(7)共同保证了可行回路;式(8)和式(9)表示客户时间窗约束;式(10)和式(11)表示决策变量的取值范围。
(1)
(2)
(3)
∀k∈{1,2,…,K}
(4)
(5)
(6)
2≤|S|≤N-1
(7)
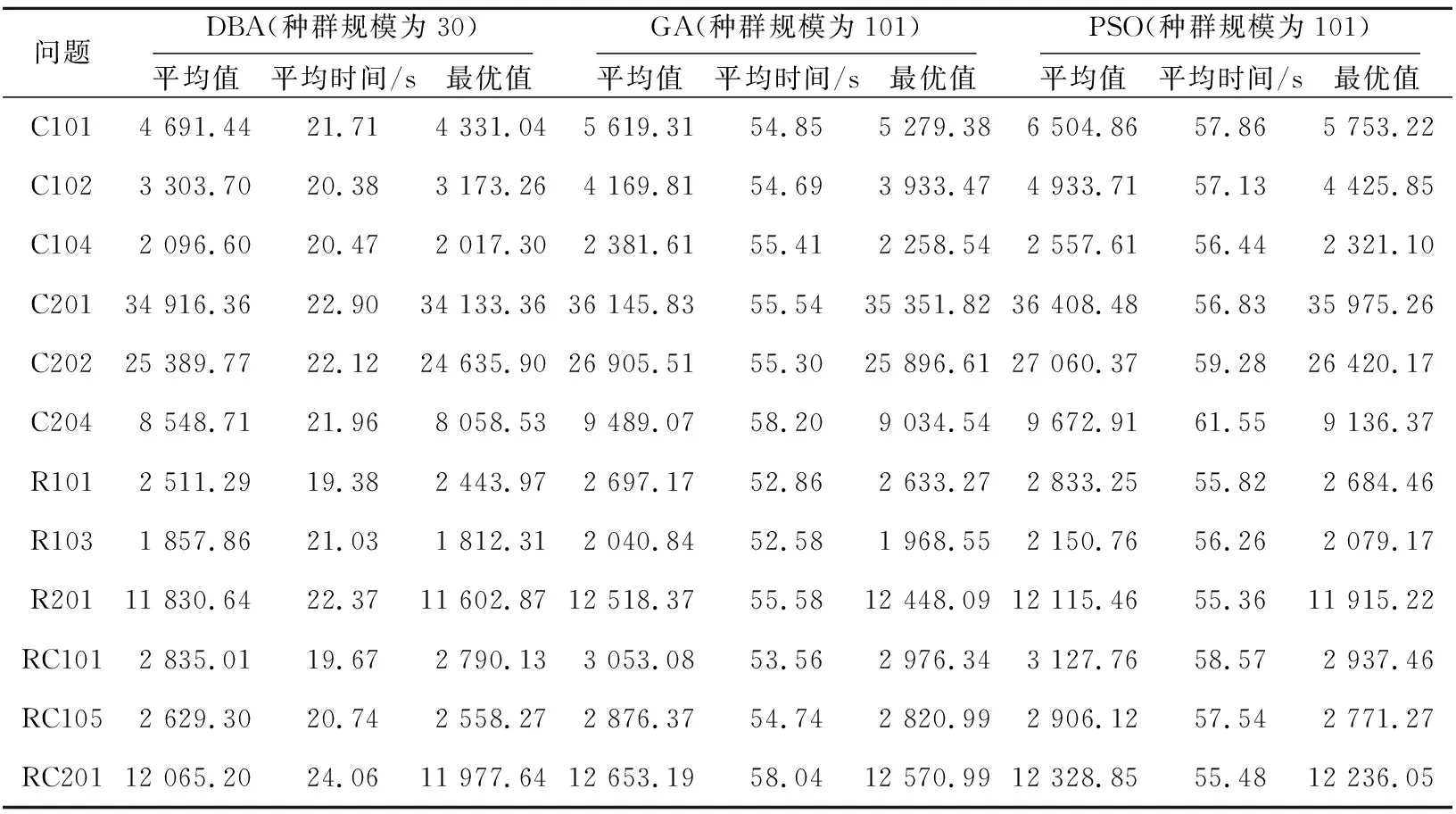
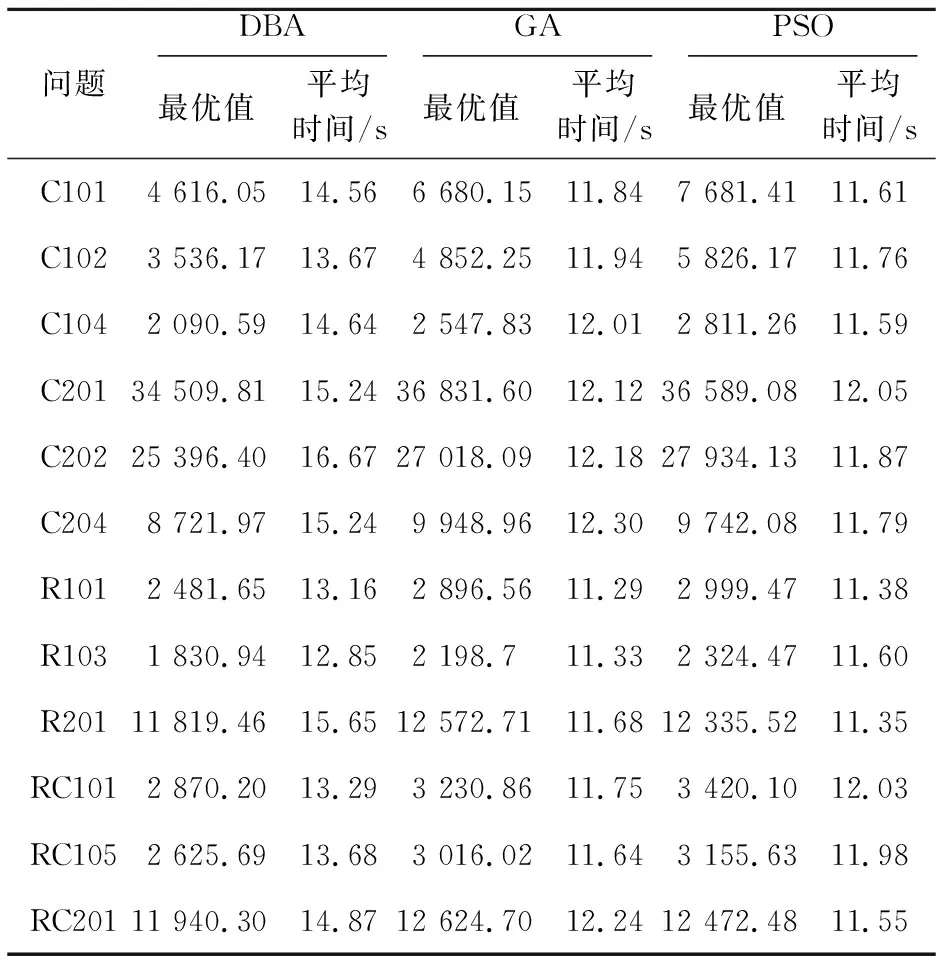
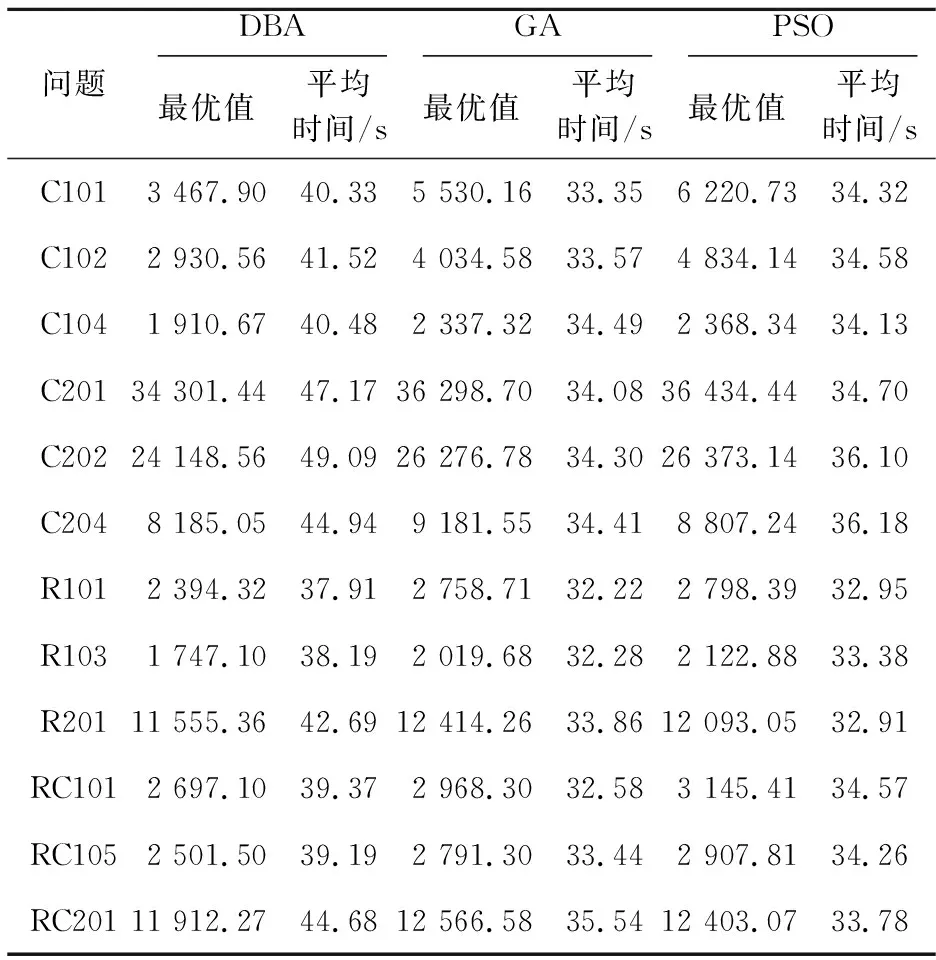
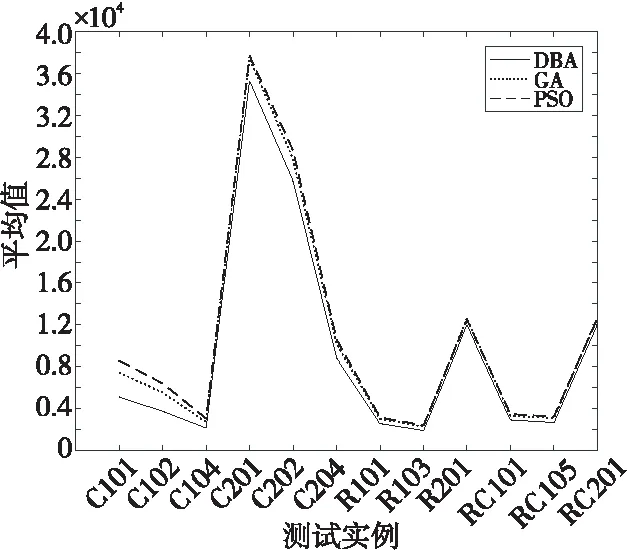
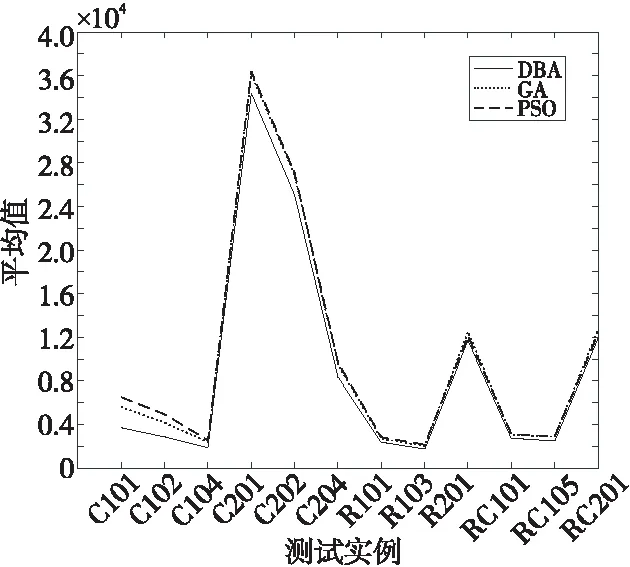
Sj (8) Aj=Ai+ti+tij,i,j∈{0,1,2,…,N},i≠j (9) xijk∈{0,1},i,j∈{1,2,…,N},∀k∈{1,2,…,K} (10) yki∈{0,1},i∈{1,2,…,N},∀k∈{1,2,…,K} (11) 蝙蝠算法BA是由Yang[22]提出的一种新型启发式算法,算法利用蝙蝠通过回声定位行为进行捕食的原理进行问题求解,具有参数少、稳定性高、求解速度快、寻优能力强等优点,已在工程优化、特征选择、故障诊断和数据挖掘等多个领域展现出较好的应用效果[23 - 27]。蝙蝠回声定位原理为:蝙蝠以脉冲的形式发射一定频率和响度的超声波,当超声波在传播的过程中遇到物体时会返回回声,通过对接收到的回声进行处理,蝙蝠可以检测到物体相对于自身的距离和方向,以及物体的大小和运动速度,从而捕食或者避开障碍物。为便于模拟蝙蝠的回声定位行为,Yang给出2个理想化规则: (1)搜索规则:蝙蝠随机飞行,同时以固定的频率、可变的波长和音量的超声波来搜索猎物。 (2)参数变化规则:蝙蝠根据自身与猎物的距离来自动调整脉冲波长和脉冲发射率,并限定声音响度在指定范围内依照给定方式由大到小变化。 算法求解过程由若干独立搜索的蝙蝠完成,算法首先将每只蝙蝠视为当前可行域内的一个解,每个解对应一个由所优化问题确定的适应值,每只蝙蝠通过调整其脉冲频率、声音响度、脉冲发射率3项参数来追随当前最优蝙蝠,使得整个种群在问题求解空间中产生从无序到有序的衍化,进而获取最优解。脉冲频率、速度和位置的更新方式如式 (12)~式(14)所示: fa=fmin+(fmax-fmin)β (12) (13) (14) Begin 初始化算法相关参数及蝙蝠的位置、速度和脉冲频率; 根据蝙蝠的初始位置计算适应度值,得出初始解,找出最优蝙蝠位置; While(t<最大迭代数) 根据式(12)~式(14)分别调整蝙蝠的脉冲频率、速度和位置; If(当前随机数>当前脉冲发射率) 在当前最优解附近根据式(15)进行局部搜索; xnew=x*+ε*μ (15) 其中,xnew表示随机扰动得到的新解;ε表示服从标准正态分布的随机向量,且ε~N(0,1);μ表示常量,且0<μ<1;x*表示当前最优解。 Endif If(当前随机数<当前声音响度,且xnew的适应度值优于x*) 接受新解,分别根据式(16)和式(17)更新脉冲发射率和声音响度; (16) (17) Endif 输出全局最优解; Endwhile End 车辆路径问题属于离散的组合优化问题,首先对所求问题中的各个变量设计编码策略,然后将其转变为蝙蝠算法可以优化的变量。假设求解问题的规模为N,将客户点编码为从1到N的不同整数。 (1)解编码策略。 针对CVRPTW问题的特性,解的编码以待访问客户点编号序列表示,解中每个分量对应一个客户点编号,因而得到解X的编码形式为:X=(m1,m2,…,mN)。其中,N表示编码长度,mi表示第i个要访问的客户点编号(mi∈[1,N],且任意mi≠mj)。 (2)速度编码策略。 vi表示蝙蝠访问到第i个客户点时的速度值,则速度的编码形式为:V=(v1,v2,…,vN)。其中,V表示速度,编码中每一个速度的值可以为正值或负值,vi∈[-(N-1),N-1]。 由于标准蝙蝠算法缺少扰动机制,存在算法后期收敛速度慢、易陷入局部最优等缺陷[28],为此引入变步长搜索策略和2元素优化2-opt操作以增加解的多样性,跳出局部最优。 (1)变步长搜索。 在搜索过程中,蝙蝠的移动步长应伴随搜索过程的进行发生改变,在算法运行初期,步长应保持一个较大值,以避免算法过早陷入局部最优;随着迭代次数的增加,步长应自适应地减小,最后保持一个较小值,使得算法后期加快收敛,得到更精确的值。标准蝙蝠算法中,蝙蝠位置的更新受ε和μ2个因子的影响,二者不能保证步长值遵循上述规则发生改变。若常量u取值较大,易使算法收敛速度变慢,若μ取值较小,则算法易陷入局部最优。 本文引入变步长搜索策略,以增加扰动机制和解的多样性。定义步长扰动因子,其计算方法如式(18)所示: τj=(Nitermax-j)/Nitermax (18) 其中,τj表示在第j次迭代时的步长扰动因子,Nitermax表示最大迭代次数,j≤Nitermax。 改进的蝙蝠算法中,蝙蝠以变步长的方式进行局部搜索,搜索方式如式(19)所示: xnew=x*+ε*μ*τj (19) (2) 2-opt优化操作。 2-opt操作即选定路径上的任意2个节点并将节点间的路径进行翻转,得到新的路径,以增加路径搜索的多样性,提高算法局部搜索能力。以7个客户点的配送为例,假设客户点为A、B、C、D、E、F、G,s为当前最优解,s={A,B,C,D,E,F,G}。以一定的概率进行2-opt操作,首先在s中随机选择不相邻的2个节点B和E,然后将2个节点之间的路径翻转获得新路径,节点B之前的路径保持不变添加到新路径中,将节点B到节点E之间的路径逆序排号后添加到新路径中,节点E之后的路径不变添加到新路径中,则得到的新路径s′={A,E,D,C,B,F,G}。 为降低算法在搜索过程中的随机性,缩小搜索范围,加快搜索速度,本文首先引入聚类操作,对所有客户点按其所在位置采用K-means算法进行聚类,使得每个客户点最终归属于若干个不同分区。本文DBA算法的适应度值根据式(1)计算,具体求解方法如下: Step1根据每个待配送客户点所需配送的货物重量,并结合车辆的载重限制把满足要求的客户点放入车辆运行路线中。 Step2如果该客户点的货物重量超出了车辆的限载量Q,则再申请1辆车,并将当前所需车辆总数加1;当遍历完所有客户点时,即可确定所需车辆总数K。 Step3每个客户点都对应唯一的时间窗,若车辆不在客户点相应的时间窗内到达,则给予一定的惩罚。 Step4计算油耗成本、违反时间窗的惩罚成本和车辆的租赁费用之和。 DBA算法实现步骤如下所示: Step1对蝙蝠位置、脉冲频率和速度进行初始化操作。 Step2将Step 1中所有初始蝙蝠个体的位置(即所有客户点)按其所处位置利用K-means算法进行分区处理。 Step3蝙蝠位置更新,即对于任意蝙蝠a,根据式(12)~式(14)分别调整其脉冲频率、速度和位置,从而产生后代蝙蝠。 Step4若当前随机数小于当前脉冲频率,则按Step 3进行全局搜索,并计算新的适应度值;否则在当前解附近根据式(19)以变步长搜索方式进行局部搜索,并以一定的概率进行2-opt操作,计算新的适应度值。 Step5若Step 4得到的适应度值小于当前最小适应度值,并且当前声音响度大于当前随机数,则利用Step 4得到的适应度值更新最小适应度值,并记录各个蝙蝠的位置,得到全局最优解,否则不更新。 Step6根据式(16)和式(17)分别更新脉冲发射率及声音响度。 Step7重复Step 4~Step 6,直到满足结束条件,输出全局最优解。 由于遗传算法、蚁群算法和粒子群优化算法是当前在CVRPTW问题求解领域应用较为广泛的群智能优化算法,而蚁群算法在求解较大规模问题时速度相对较慢,因此,本文选取GA和PSO算法进行对比实验。实验测试环境为Windows 10 64位操作系统,CPU为3.4 GHz,内存为4.0 GB;仿真实验平台为Matlab R2017b。 Solomon数据集是目前带时间窗车辆路径问题最常用的标准测试库,按照节点间的位置关系可以将Solomon数据集中的测试数据分为C、R和RC 3大类,每类问题又划分为1和2 2个子类。3大类问题客户点坐标及时间窗设置方式不同,其中C类数据中节点呈集簇式分布,节点分布于若干中心位置附近;R类数据中节点呈随机分布,节点位置间无明显集簇关系;RC类数据介于两者之间,部分节点呈随机分布,部分节点呈集簇式分布。子类1中问题的时间窗设置相对集中,子类2中问题的时间窗设置相对分散,且时间跨度较大。为了更全面地验证本文算法求解效果,本文分别选取C1、C2、R1、R2、RC1、RC2问题中12个经典测试实例(见表1,其中,测试实例C101、C102、C104都属于C1类问题。C101、C102、C104是Solomon测试集中的测试实例名称,其问题规模均为101,不同测试实例之间的客户点分布不同),分别使用DBA、PSO和GA算法对每个实例进行10次计算,所有测试均采用全浮点数运算,算法所得最优解为10次计算所得最小值。 算法中各参数取值如下:DBA中脉冲频率的最大值fmax=1,脉冲频率的最小值fmin=0,声音响度的衰减系数p=0.9,搜索频率的增强系数γ=0.9,声音响度A∈(0,1),脉冲发射率r∈(0,1),早于和晚于时间窗到达的惩罚系数e=l=0.35,单位距离油耗成本b=0.35,单位车辆的费用c=100,车辆的最大载重量Q=200;GA算法中交叉概率pc=0.3,变异概率pm=0.2;PSO算法中惯性权重因子w=0.2,加速系数C1=C2=2。 表1~表3给出了种群规模等于城市规模数,迭代次数分别为200,600和1 000时3种算法所得最优值及平均耗费时间。 Table 1 Optimal values and average time consumption of three algorithms when iteration number is 200表1 迭代次数为200时3种算法最优值和平均耗费时间 Table 2 Optimal values and average time consumption of three algorithms when iteration number is 600表2 迭代次数为600时3种算法最优值和平均耗费时间 从表1~表3可以看出,种群规模相同的情况下,迭代次数分别为200,600和1 000时,DBA算法对于12个实例所得最优值均在很大程度上优于GA和PSO算法的,GA算法获得的最优值多数优于PSO算法的。在平均时间耗费方面,DBA算法稍长于GA和PSO算法。 为进一步验证DBA算法性能,分别针对各问题计算GA或PSO算法最优值与DBA算法最优值之差与 DBA算法最优值的百分比,得到如下结果:表1中,C101问题改进效果最好,DBA算法相对GA和PSO算法分别改进44.71%和66.41%;对于RC201和R201问题,DBA算法相对GA和PSO算法改进效果较差,前者分别改进了5.73%和4.46%,后者分别改进了6.37% 和4.37%;对于表1中12个实例,DBA算法相对GA和PSO算法平均改进了17.28%和24.11%。表2中,C101问题改进效果最好,DBA算法相对GA和PSO算法分别改进了59.47%和79.38%;RC201问题改进效果最差,DBA算法相对GA和PSO算法分别改进了5.49%和4.12%;对于表2中12个实例,DBA算法相对GA和PSO算法平均改进了17.64%和22.61%。表3中,C101问题改进效果最好,DBA算法相对GA和PSO算法分别改进了59.38%和73.69%;对于C201和RC201问题,DBA算法相对GA和PSO算法改进效果较差,前者分别改进了3.71%和5.54%,后者分别改进了6.26%和3.43%;对于表3中12个实例,DBA算法相对GA和PSO算法平均改进了18.02%和21.24%。总体来看,3种问题中C类问题改进效果最好,R类问题其次,RC类问题最差;每种问题内1类问题相对于2类问题的改进效果更好。 Table 3 Optimal values and average time consumption of three algorithms when iteration number is 1 000表3 迭代次数为1 000时3种算法最优值和平均耗费时间 图1~图3分别给出了与表1~表3相同条件下3种算法分别对12个测试实例进行10次运算所得解的平均值随问题规模变化的曲线图。图4给出了对于表1~表3中12个实例,DBA算法分别相对于GA和PSO算法的平均改进百分比条形图。 Figure 1 Change curves of average values of three algorithms when population size equals to the number of cities and iteration number is 200图1 种群规模等于城市数时迭代 200次3种算法平均值变化曲线 Figure 2 Change curves of average values of three algorithms when population size equals to the number of cities and iteration number is 600图2 种群规模等于城市规模时迭代 600次3种算法平均值变化曲线 Figure 3 Change curves of average values of three algorithms when population size equals to the number of cities and iteration number is 1 000图3 种群规模等于城市规模时迭代 1 000次3种算法平均值变化曲线 Figure 4 Average improvement percentage of DBA relative to GA and PSO for the 12 problems图4 对于12个问题DBA分别相对于 GA和PSO的平均改进百分比 从图1~图3及前述数据分析结果可以发现,DBA算法求解所得最优值及平均值均优于GA和PSO算法的,GA算法相对于PSO算法获得较好最优解的比例更高,且在迭代1 000次时的DBA算法相对于GA算法改进效果最好。 从图4可以看出,DBA算法相对于GA算法的平均改进百分比最大为18.02%,最小为17.28%;DBA算法相对于PSO算法的平均改进百分比最大为24.11%,最小为21.24%。上述图形及数据表明,本文所设计的DBA算法相对GA和PSO算法具有较好的求解效果。 表4给出了迭代次数为1 000时,种群规模为30的DBA算法、种群规模等于城市规模数的GA和PSO算法所得平均值、最优值和平均耗费时间。 从表4可以看出,迭代次数相同的情况下,种群规模为30的DBA算法所得最优值、平均值和平均时间耗费均优于采用较大规模种群的GA和PSO算法。在上述12个测试实例中,种群规模为30的DBA算法的平均求解时间相对于同等规模的GA和PSO算法分别加快了158.16%和168.98%;GA和PSO算法的最优值相对于DBA算法的平均值的平均改进百分比分别为6.73%和9.27%,最好改进百分比分别为19.06%和33.97%。数据分析结果表明,DBA算法在问题求解精度和求解效率方面均有较为明显的优势。 带时间窗和容量约束的车辆路径问题在现实中有着广泛的应用,对该问题进行优化的研究从未停歇。本文研究了求解该问题的离散蝙蝠算法,利用K-means算法对客户点按其所在位置进行聚类,在DBA算法中引入了变步长搜索策略和2-opt操作进行局部搜索。 实验结果表明:所设计的离散蝙蝠算法具有较快的收敛速度和较强的寻优能力,能够有效降低配送成本。本文设计的算法只是对标准蝙蝠算法的初步改进,对测试库内子类2中问题改进效果相对较差,后续研究中将考虑对子类2问题的时间窗进行聚类处理,并将蝙蝠算法与其它智能算法思想相结合,以进一步提高算法的求解性能。 Table 4 Optimal values and average time consumption of three algorithms with different population sizes when iteration number is 1 000表4 迭代次数为1 000时3种算法在不同种群规模下的最优值和平均耗费时间3 模型求解的改进蝙蝠算法

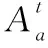
3.1 编码策略
3.2 局部搜索策略
3.3 算法实现
4 仿真实验



5 结束语