非惯性系中大摆角单摆周期的积分形式及数值分析
2021-09-24赵清锋
赵清锋
(武汉市卓刀泉中学建和分校 湖北 武汉 430065)
单摆问题是基础物理中的重要模型,在物理学中有广泛的应用,对于单摆的研究非常多,而其中的研究多限于固定悬挂点单摆做圆周运动的周期,包括大摆角周期公式、有无空气阻尼的影响、不同摆次单摆的周期、解析解等[1~6].对于非惯性系单摆运动问题在近几年中学生物理竞赛中出现的次数较多,相关文献也对此有研究,文献[7]用不同方法计算了无固定悬挂点单摆周期,文献[8,9]利用机械能守恒分析了匀加速直线运动系统和定轴转动非惯性系统单摆周期,但都只分析了小角度振动周期,对于非惯性系中大摆角振动问题研究较少.基于此,本文从无阻尼非惯性系出发,对悬点可动单摆周期进行了计算,得出周期的积分形式,并应用数值计算与相关研究结果进行对比分析.
1 悬点可在水平方向无阻尼运动单摆周期的积分形式
考虑无阻尼情况,质量为M的小环A套在光滑的水平固定杆上,摆球B的质量为m,A和B用一长度为l的轻绳连接[模型来源2019年全国中学生物理竞赛(江苏赛区)第一轮复赛第15题,教材中也有对应模型[10],如图1所示].本文以摆线与竖直方向初始夹角为θ进行计算(原题中摆线从水平位置自由释放).

图1 悬点无阻尼单摆模型
由于杆是光滑的,小环A和摆球B在水平方向所受合外力为零,系统质心在水平方向的坐标保持不变,即质心位置到摆球B的距离应该为
(1)
考虑悬线在摆动过程中质心水平坐标不变,而竖直坐标在变化,为方便研究,取摆线水平时质心位置为坐标原点O,建立直角坐标系如图2所示(其中摆线与竖直方向夹角为θ时,令OB与水平方向的夹角为φ,l2=l-l1,vB为摆球B的速度,φ为摆球B此时运动方向与水平方向的夹角.

图2 悬点无阻尼单摆坐标系及相关物理量
分析可知,摆球B对应的横纵坐标分别为
x=l1sinθy=-lcosθ
联立两式消去θ可得摆球运动的轨迹方程为椭圆的一部分,如下
(2)
对式(2)求导可得椭圆上此点切线斜率为
(3)
角度φ为摆球B此时速度的方向与水平方向夹角,为方便后文计算,进一步化简可得
(4)
由于水平方向外力之和为零,所以水平方向动量守恒
MvA=mvBcosφ
(5)
将式(1)、(4)带入式(5)可得
(6)
设摆绳初始时刻与竖直方向的夹角为θ0,由于系统机械能守恒
(7)
将式(6)带入式(7)可得
(8)

(9)
以O为圆心,dφ角度对应的圆弧长度即为
(10)
而小球轨迹并非圆弧,而是椭圆,根据几何关系可得dφ对应的轨迹弧长
(11)
根据式(9)和(11)即可得到摆球周期的积分形式
(12)
φ0为摆绳初始时OB与水方向的夹角.由于质心水平位置坐标不变,可将θ用φ取代
(13)
由式(3)和式(13)可将φ用φ取代
(14)
将式(13)和式(14)带入式(12)即可进行数值积分计算[11].
对于此类模型的周期,竞赛题答案多采用受力分析结合非惯性系动力学方程求解,这种方法通过数值计算也可求出模型的准确周期或频率,相关文献给出其他方法,当摆角θ较小时取sinθ≈θ,然后近似计算小角度非惯性系单摆周期[7,8].在教材中有定义M水平坐标x1和θ为广义坐标,然后利用拉格朗日方程得到微分方程组[10]

(15)
2 数值计算周期与近似周期的比较分析
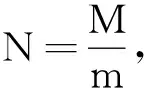

表1 数值计算周期与近似周期的比较
从数值计算的数据进一步可以得到,大摆角悬点可动单摆周期变化随着N的减小而更明显,当N值很大时,其周期与悬点固定单摆周期基本一致(本文计算均为无阻尼情况,N=107对应周期与文献[1]周期存在微小差距,与数值计算精度有关).

l为摆线的长度,g为重力加速度,M和m分别代表悬点和摆球的质量.
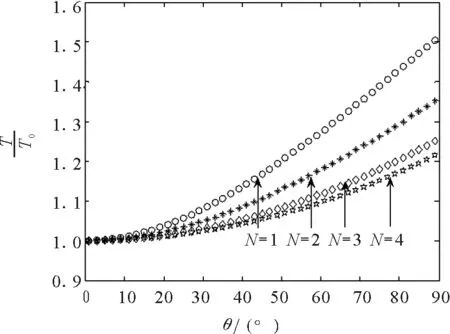
图随θ的变化关系

3 结束语

