伯努利方程在电介质流体中的应用
2021-09-24冯子江
冯子江 鲁 斌
(浙江省余姚中学 浙江 宁波 315400)
伯努利方程在力学中有广泛的运用.由于其形式
式中不含电学量,故其在电学中应用甚少.在电介质流体的相关问题中,可将伯努利方程作适当推广,以拓宽其应用范围.
1 电势能密度的导出
如图1所示,一个电偶极子在非均匀场中的受力
(1)
其中p=ql为电偶极矩.

图1 电偶极子在非均匀场中的受力
我们考虑体积为dV的分子团,单位体积内带有n个电偶极子,现沿x方向由A到B,电场力做功
(2)
由极化强度矢量
(3)
将式(3)代入式(2),有
则有
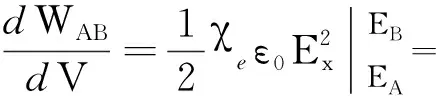
(4)
则
(5)
即为电介质在电场中的电势能密度.
2 伯努利方程在电介质流体中的推广
对于体积为ΔV的流体,根据伯努利方程,有
(6)
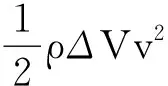
基于此,则在电介质流体定常流动的情况下,对原有的伯努利方程进行推广,即
(7)
当然,若流体为其他性质的流体如磁介质等,方程还可做进一步相应的推广.
3 电介质流体的平衡问题
如图2所示,水平放置的平行板电容器,一块极板在液面上方,另一块极板浸没在液面下,液体的相对介电常数为εr,密度为ρ,传给电容器上下极板电荷面密度分别为σ,-σ后,电容器中的液面可能升高多少?[1]

图2 带有电介质流体的平行板电容器
3.1 能量极值求解法
如图3所示,设极板面积为S,平衡后,新液面高出原液面的距离为h.
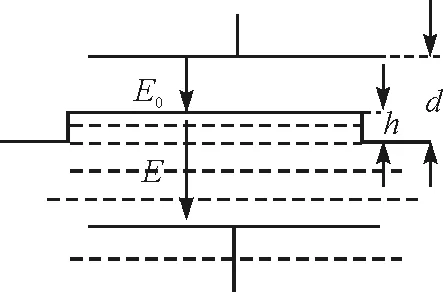
图3 分析图
在空气中
(8)
在介质中,总场强
(9)
由于电场的不均匀性,电场能量分为两部分,一是介质部分电场能量Ep1
(10)
二是真空部分电场能量Ep2
(11)
另外,介质液体还具有重力势能Ep3
(12)
则总能量
由于平衡位置能量取极值,则有
化简得到
(13)
3.2 运用电势能密度的压强性质求解法
为解决本题,我们构造一系列过程,如图4所示.
体积为ΔV(ΔV→0)的分子团,处在A,B,C这3处时具有不同的电势能密度,即对应不同的压强.
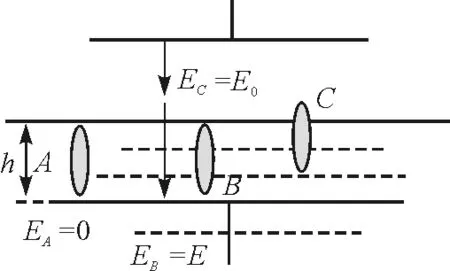
图4 构造过程
第一个过程,将分子团从电容外一点位置A(PA=0)移动到电容内等高的位置B,发生一段虚位移.
由于B点的电势能小于A点,则分子团有从A向B侧向进入的趋势.产生的压强差即为
(14)
第二个过程,从位置B移动到几乎等高的介质表层位置C时
产生的压强差即为
(15)
这里应该注意的是PC和EC的取值.此时分子团处在E0的外场中受力,所以
EC=E0

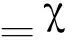
(16)
故由于C点的电势能小于B点,则分子团有从B向C纵向上拱的趋势.代入后,即可得到
(17)
(18)
根据受力平衡,有
(19)
3.3 关注始末状态运用伯努利方程求解法
我们也可以直接用伯努利方程解决问题.构造一个从A到平衡后最高点D的过程.满足
(20)
这里p的意义为由于水和大气压强所引起的总压强.由于A点贴近液体表面,则有
pA≈pD=p0
又由于vA=vD=0,PC=PD,EC=ED,代入方程有
(21)
又h=hD-hA,则
(22)
4 结束语
运用电势能密度与推广后的伯努利方程解决电介质流体的平衡问题,为我们处理电介质问题提供了新的思路,为进一步推广伯努利方程提供了可行的范式.
