基于光纤应变传感器的柔性管道形状重建应用研究
2021-09-24李孝友钱思宇刘盛春陈雪峰
李 伟,李孝友,钱思宇,刘盛春,陈雪峰
(黑龙江大学 电子工程学院 黑龙江省超构材料物理与器件重点实验室,哈尔滨 150080)
0 引 言
目前,针对长输管道的健康检测方法主要有射线法、超声波法、漏磁法、水下遥控机器人和负压波法等[1],这些方法存在自身应用局限性,如射线法适合对局部区域范围内进行检测,长距离检测速度很慢,耗时较长;超声波法、漏磁法和水下遥控机器人检测法技术比较成熟,但其工作效率低,需要逐点检测,或只能间断性进行检测,仅适用于没有过多弯头和连接处的管道;负压波法难以对微小缓慢泄漏进行检测,容易受到噪音的影响,误报率相对较高。光纤传感器因其抗电磁干扰、绝缘性好、耐腐蚀、尺寸小、灵敏度高和可进行长距离监测等优势在传感领域中占据了重要位置,在健康监测方面具有显著优势,在对待测物进行应变、温度和加速度等物理量的测量方面具有广泛应用,尤其是在海洋工程、智能医疗和航空航天等形状监测领域具有广阔的发展前景[2]。光纤形状传感技术在智能医疗领域得到大量应用,如用于检查大肠部位的肿瘤或溃疡等疾病的肠道内窥镜、治疗肾结石的输尿管内窥镜,特点是小型化和精细化,科研人员改进并优化了很多重建算法。2014年,沈林勇等[3]提出了一种基于光纤光栅形变测试技术的智能内窥镜形状重建和可视化的方法,实现了基于曲率的曲线形状重建技术。2019年,章亚男等[4]研究了沿基材母线等间隔分布的FBG形状传感器的应变传递规律,并将其引入形状重建中,改进了FBG形状传感器的重建算法,末端相对定位精度由原来的3.5%提高到2.7%。2020年,张伟冬等[5]设计了一种FBG传感元件结构,可有效提高传感元件的应变传递效率,减小了传感系统形状重建位置误差,提高了光纤形状传感器的形状重建定位精度。Yi X H等[6]提出了一种分离弯曲和扭转的理论方法,设计了一种将3根光纤封装在柔性杆表面,形成三角形光纤光栅传感器阵列的形状传感器。朱伟涛等[7]提出一种螺旋布设光纤光栅形状传感方法来实现微创手术软体操作器弯曲伸缩运动时的形状测量,证明了该方法可用于软体操作器形状传感与重构。
光纤形状传感技术在海洋工程和航空航天等领域同样有重要的应用,如航空航天器的柔性结构形变状态主动监测、海底电缆的形变状态监测和海洋柔性石油管道的应变和形态监测等,相对智能医疗领域来说,其呈现大型化和环境复杂化。2012年,美国LUNA公司将总长为30 m多芯光纤形状传感器布设在长度为10 m左右的柔性结构表面,通过重构多芯光纤空间位置获得被测表面的空间变形[8]。2014年,任鹏等[9]将分布式布里渊光纤传感技术并结合空间曲线重构算法应用在立管姿态监测上,利用聚合物柔性管材进行了两种立管作业工况下的验证性实验。2017年,吴仲台等[10]开发了一种管线弯曲变形检测装置,将一对互成90°的光纤光栅传感器粘贴在形状记忆合金丝上,在管道内拖动该装置,管道的弯曲将导致记忆合金丝的曲率改变,利用光纤光栅传感器测量记忆合金丝在不同位置的曲率,通过不同位置的曲率计算管道的变形。2018年,曲道明等[11]为解决变形机翼柔性蒙皮形状实时监测问题,研究了柔性蒙皮形状光纤传感及重构方法。
本文将单根反射率为0.05%的弱光栅阵列沿轴向布设于长度为7.6 m的柔性管道表面,进行了弯曲应变监测并利用基于圆弧模型的曲线算法对柔性管道在3种不同弯曲情况下的二维形状进行了重建。通过弱光纤光栅传感技术与圆弧模型曲线算法相结合,实现了柔性管道的二维形状重建,监测数据与柔性管道实际几何形态吻合较好。
1 光纤光栅应变及温度特性分析
光纤光栅是通过一定方法在光纤纤芯形成永久性折射率周期性变化的光纤器件[12],常用的刻写方法主要有相位掩模法和飞秒直写法[13-15]。当宽带光在均匀光纤光栅中传输时,光纤光栅会通过波长选择作用反射特定波长的光,并透过其他波长的光。光纤光栅对温度和应变非常敏感,当外界相关物理量发生变化时,光纤光栅反射谱的中心波长会发生漂移,其工作原理见图1。

图1 光纤光栅的工作原理
光纤光栅的反射波长与折射率、周期的关系式[16]为
λB=2neffΛ
(1)
其中心波长λB取决于光栅栅格周期Λ和光栅的有效折射率neff,这2个参数会随着外界温度、应变等物理量的变化而变化。对光纤光栅施加均匀轴向拉伸或压缩的作用力和对其进行加热或冷却的温度干扰,光栅波长值会沿轴向产生相应的偏移。因此λB可用应变ε和温度T来表示[17]:
λB=2neffΛ=2neff(ε)Λ(ε)+2nefff(T)Λ(T)
(2)
全微分处理后可表示为
(3)
将式(2)与式(3)相除可得
(4)
式(4)为光纤光栅的传感表达式,进一步简化得
(5)
式中:Pe为弹光系数,其取值会随着材料的不同而改变,常用的光纤材料为石英,Pe一般取0.216 nm·με;εz为光栅沿轴方向的应变;αΛ为热膨胀系数;αn为光纤热敏感系数;ΔT为光纤温度变化量。
在温度一定的情况下,省略式(5)中等号右边的第2项,光纤光栅的应变为
(6)
2 基于圆弧模型的二维形状重建算法
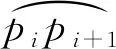
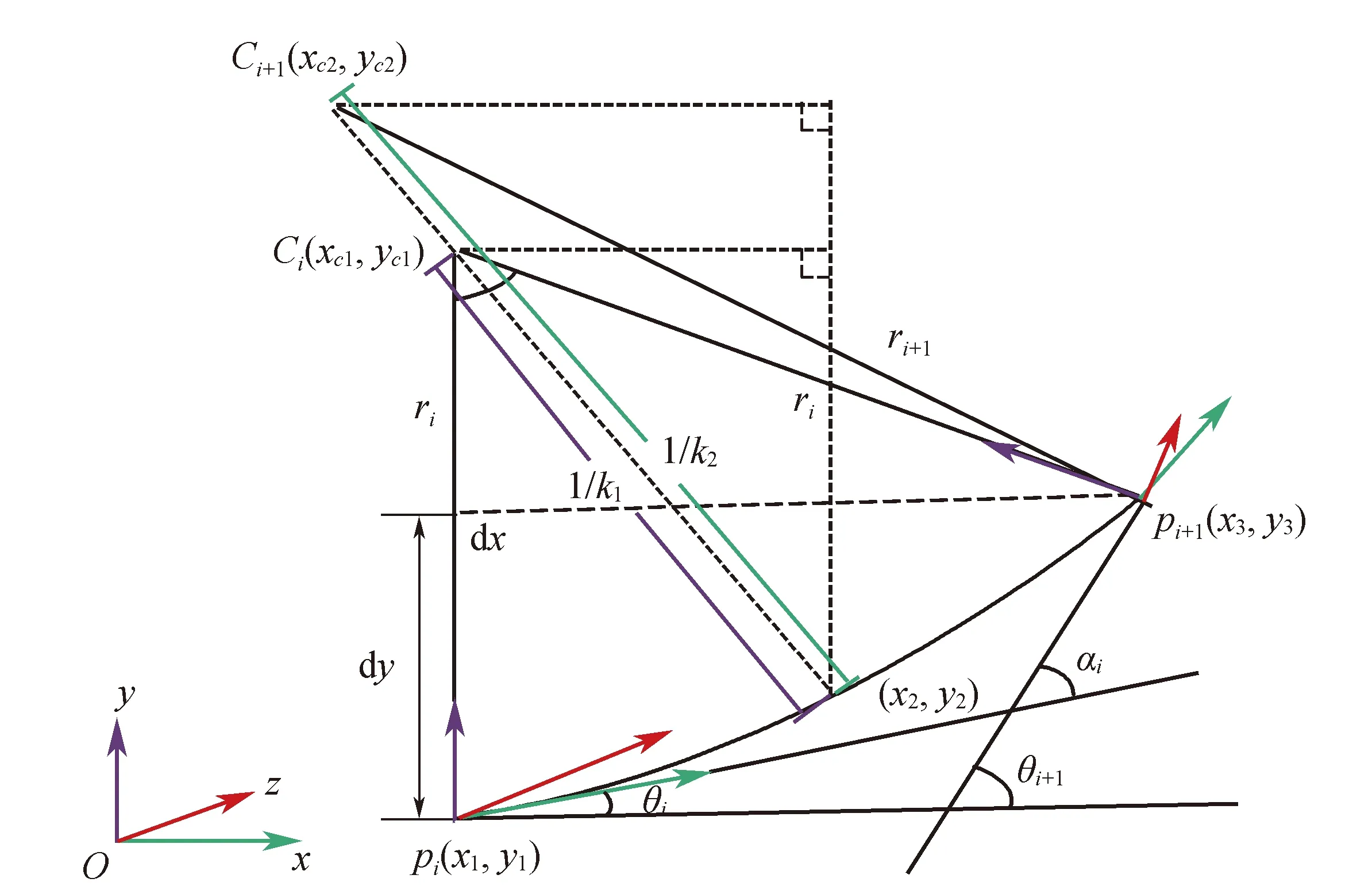
图2 基于圆弧模型的二维形状重建原理图
αi=θi+1-θi
(7)

(8)

(9)
利用Matlab工具实现该算法的编写。将柔性管道总长度平均分成若干段,每段的单位长度为dl,已知其曲率为k。根据几何原理,用半径为1/k的圆上长度为dl的圆弧进行近似处理。之后每一段都从上一段结尾处开始接上长度为dl、曲率半径各异的圆弧,最终组成完整的曲线。
读取各段曲率到矩阵K后,根据矩阵大小初始化单位dl曲线端点横坐标x、曲线端点纵坐标y、圆心横坐标xc、圆心纵坐标yc、端点与圆心连线和水平轴所成角度T的0矩阵。设置起点坐标为(0,0),即x(1)=0、y(1)=0;起始圆心坐标为(0,-1/K(1)),即xc(1)=0、yc(1)=-1/K(1)、T(1)=π/2。
根据几何性质,每段单位长度的圆弧对应圆心应该满足:
(10)
(11)
(12)
根据上述方程组创建函数Myfun用于求解圆心坐标。以4段单位长度为例,从i=2到i=4开始循环。由T(i)=T(i-1)-dlK(i-1)可得该弧度末端与圆心连线和水平轴所成角度;由x0=cos(Theta)./K(i-1)+xc(i-1)、y0=sin(Theta)./K(i-1)+yc(i-1)绘制该段圆弧、并取圆弧末端坐标赋值给x(i)和y(i),其中Theta是T(i)到T(i-1)的均匀分布矩阵;考虑到最后一段结束后不需要计算下一段的圆心坐标,如果i≤3则调用函数Myfun计算出下一段圆弧的圆心坐标。
3 解调方法与封装方法
3.1 弱光栅阵列解调方法
弱光栅反射率极弱,峰值反射率通常低于-20 dB[18],对温度和应变非常敏感。由于反射率低,相同周期的光纤光栅可相互穿透,基于时分复用技术可实现在同一根光纤上复用多个弱光栅传感单元。弱光纤光栅结合了光纤光栅的传感优势和光时域技术的定位优势,可实现长距离工程的实时监测。
利用可调谐脉冲光源和光时域定位技术进行解调的系统结构见图3,通过内置的可调谐激光器扫描输出不同波长的连续光,经过脉冲调制和放大后进入刻有弱光栅阵列的光纤中,光电探测器对经弱光栅阵列反射光进行高速采集,通过改变可调谐光源的输出波长,计算弱光栅传感器的中心波长,根据传感器的波长特征参数计算所有弱光栅传感器的物理数值。该解调设备可识别波长为1 527 ~1 568 nm,波长分辨率为1 pm,能够实现16个通道同步采样,每个通道的弱光栅数量为30个。按时域反射方式定位分析,得出各位置处光栅的光谱图。
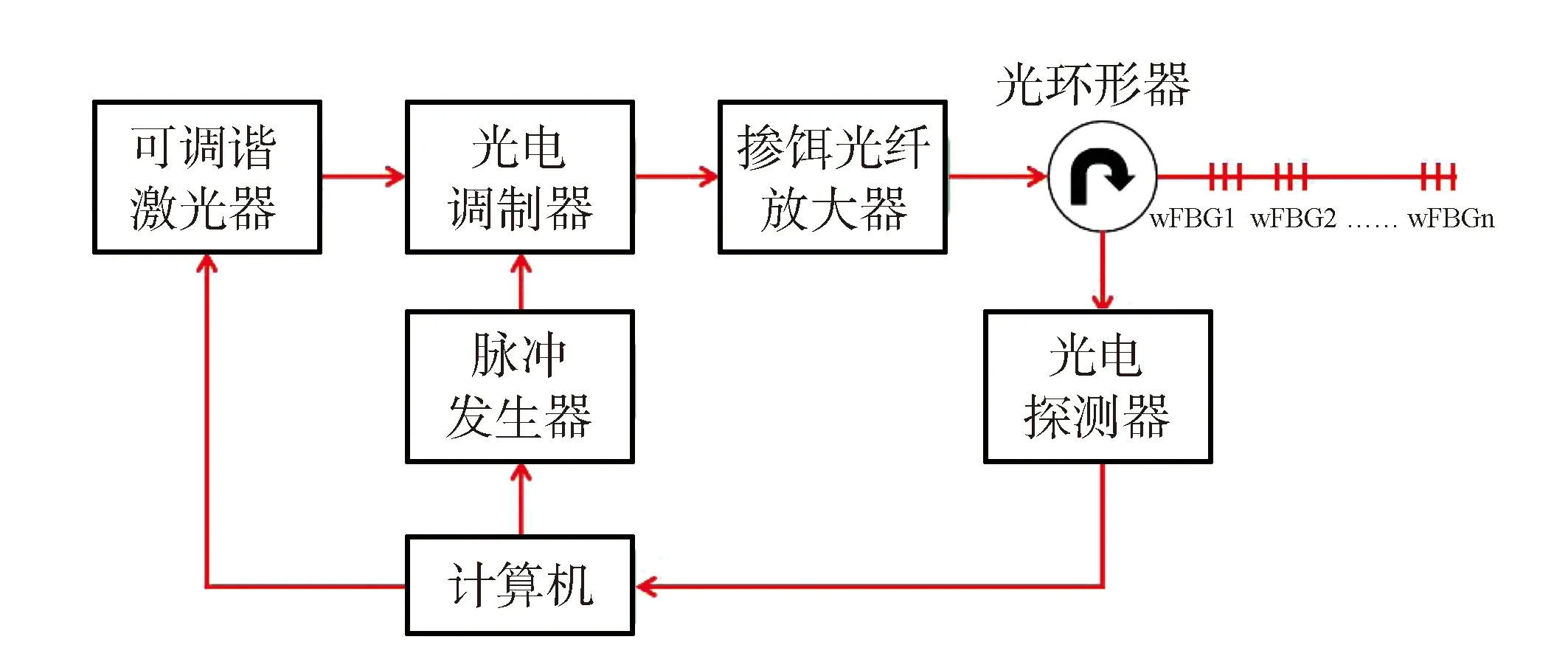
图3 弱光纤光栅应变解调系统
3.2 弱光栅传感阵列的封装方法
考虑到光纤传感器在管道上的实际应用和裸光栅阵列容易断裂的特性,利用海翠(Hytrel)护套将裸光栅传感阵列加工成具有紧密传递性能的应变感测光缆,能较好反映管道的应变情况。光栅之间的距离为1.0 m,传感器的应变量程为0~20 000 με,见图4(a)。
使用的柔性管道材质为高密度聚乙烯(HDPE),该单层内芯管的长度为7.6 m,外径和内径分别为116 mm和106 mm。在柔性管道表面绘制出粘贴区域,利用角磨机打磨使其表面平整,将环氧树脂胶溶液与固化剂按5∶2的比例混合,直至环氧树脂胶中没有拉丝且呈透明状为止。由于胶体固化时间较长,为防止应变感测光缆两端因不受力而收缩,需将分布式应变感测光缆两端加预应力进行校准并固定,随后将环氧树脂胶沿绘制好的粘贴区域均匀注入,室温下静置24 h,柔性管道表面固化成型后的应变感测光缆见图4(b)。黑线之间即为封装在柔性管道上的应变感测光缆。

图4 传感器的封装方法及布设方式
4 应变监测及形状重建
4.1 曲率标定及应变监测
考虑到弱光栅传感阵列的应变量程远小于柔性管道7%的应变量程,为防止管道弯曲程度过大而造成传感器损坏,计算在理论上柔性管道发生最大应变时传感器能够承受的最小弯曲半径为10 m。鉴于柔性管道的外径较大且长度较长,因此在地面绘制弯曲半径分别为20、17、15、13、11、10 m的圆弧,用于传感器的曲率标定。
当柔性管道的弯曲半径为13 m时,监测到第2个和第3个栅点的波长值出现了零值,但随着弯曲半径逐渐恢复到15 m以后,其波长值恢复,说明弯曲半径小于15 m以后的应变测量值已超出传感器的应变量程,因此,实验中仅测量了弯曲半径分别为20、17、15 m情况下的反射中心波长值。在实验中未达到理论弯曲半径为10 m的原因可能是由于人工滴胶导致某些栅点涂覆的胶厚度不一,造成应力集中的现象。因此,仅展示弱光栅传感阵列正向弯曲的数据。柔性管道弯曲程度见图5。

图5 柔性管道发生弯曲情况
弱光栅传感阵列位于柔性管道外侧进行正向弯曲情况下的曲率标定结果见图6(a),横坐标表示弱光栅传感阵列的反射中心波长偏移量,纵坐标表示弯曲曲率值。可见,5个栅点的反射中心波长偏移量—弯曲曲率都具有单调性,并且随着柔性管道曲率的增大,弱光栅传感阵列的反射中心波长偏移量增大。在实验环境温度保持恒定的情况下,通过式(6)计算出了弱光栅传感阵列上5个密集传递分布式光纤光栅在3种不同弯曲程度下的应变值,见图6(b)。
图6 曲率标定及各个栅点的应变值
4.2 柔性管道重建结果分析
弱光栅传感器经过曲率标定后,得到反射中心波长偏移量与弯曲曲率关系,通过线性拟合得到一次函数(图7),表达式为

图7 线性拟合一次函数
k=0.005 101Δλ+0.046 05
(10)
式中:k为弯曲曲率;Δλ为中心波长的变化量。
将柔性管道的弯曲半径分别设置为20、17、15 m,对柔性管道在这3种弯曲半径下的二维形状进行重建(图8)。图8(a)、8(b)和8(c)分别为管柔性道在这3种情况下的真实形状和重建形状,其中红色线段表示管道的真实形状,蓝色线段表示重建后的管道形状。图8(d)为3种不同弯曲半径下管道重建形状的结果对比。经过计算,当柔性管道弯曲半径分别为20、17、15 m时,重建后的误差分别对应为9.16%、1.02%、7.05%,达到了对柔性管道进行二维形状重建的目的。
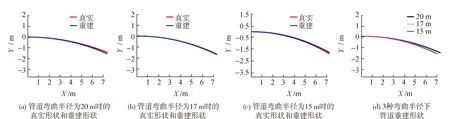
图8 不同弯曲半径下管道真实形状和重建形状
柔性管道重建结果中存在一定的误差,经过分析后,考虑出现该误差的原因主要有:①各个光栅的栅距稍大,容易遗漏栅区之间的应变信息,由于得到的数据点有限,在曲率标定过程中出现一定的误差;②受曲线重建算法自身迭代的影响,每次迭代计算后的末端点作为下一次迭代计算的起始点,会导致误差累积,若其中一个传感点出现了偏差,则该偏差随着迭代次数的增加而逐渐增大。
5 结 论
针对柔性管道在长期使用过程中产生过度弯曲和大应变这2种失效机制,为实现柔性管道的形态弯曲可视化监测对管道失效进行评估,本文提出弱光纤光栅阵列传感技术与基于圆弧模型的曲线重建算法相结合的方法,对高密度聚乙烯柔性管材进行了应变监测和3种弯曲半径下的二维形状重建实验,实验结果表明监测数据与柔性管道实际几何形态吻合较好,误差在工程允许的范围内。该技术可通过进一步优化将其应用于海洋工程领域,对柔性管道的形态监测具有重要意义。
