DMD衍射效应及其产生的杂散光分析
2021-09-23袁夕尧黄蕴涵许熠宸秦铭泽李文轩
袁夕尧,胡 源,黄蕴涵,许熠宸,秦铭泽,李文轩
(1.长春理工大学 光电工程学院,吉林 长春 130022;2.光电测控与光信息传输技术教育部重点实验室,吉林 长春 130022)
引言
数字微镜器件(digital micromirror device,DMD)是一种反射式空间光调制器,因具有高分辨率、高光学效率、高对比度等优势,被广泛应用于投影系统中。它是由一系列高反射表面镀铝的微小镜片按照面阵排列组成,每个单元均能在数字电信号的控制下,以其对角线为轴进行±12°的偏转,通过每个微小镜片的翻转,控制每个单元光信号的反射方向,从而达到光学调制的目的[1-2]。由于它的微小尺寸会带来一定的衍射效应,导致系统产生杂散光,进而降低图像对比度和系统信噪比等[3],因此,分析DMD 的衍射效应是十分必要的。
目前,已有很多学者根据DMD 结构及工作原理,将其等效为类似于闪耀光栅的结构模型,并利用光栅理论对其进行相应的分析。Walter Duncan 等人提出了将DMD 等效为闪耀光栅的模型,认为闪耀角即为镜元的倾斜角[4]。许富洋等人提出了一维闪耀光栅模型,认为光栅的栅距即为镜元宽度[5]。Joseph Rice 设计了一种DMD 衍射效率的测量系统,将其等效为二维平面光栅模型[6]。陈笑等人基于夫琅禾费衍射理论,构建了DMD 的衍射模型[7]。韩庆、熊峥等人基于傅里叶分析方法,建立了DMD 衍射的数学模型并分析其衍射效率[8-9]。
上述衍射模型都能很好地体现DMD 的衍射特性,对DMD 的应用均有一定的参考和指导意义,但均未将衍射效应与杂散光分析相结合。本文着重分析由DMD衍射效应产生的杂光,基于严格耦合波理论对DMD 进行建模仿真,分析了不同波段和入射角度对DMD衍射效应的影响。通过光线追迹分析计算了在投影系统中不同波长和F数的DMD 衍射杂光能量占比,分别从物理光学和几何光学的角度对DMD 的衍射特性进行分析描述,为含有DMD 的复杂光学系统设计及杂散光分析奠定基础。
1 DMD 衍射特性
1.1 衍射特性基本原理
结合DMD 的微观结构和工作原理,将其等效为二维矩形光栅。由于DMD 尺寸在波长量级,且每个微镜片呈周期性排布,在红外波段,标量衍射理论并不适用分析其衍射效应,计算得到的结果误差较大。因此本文采用严格耦合波理论(rigorous coupled wave analysis,RCWA)作为DMD衍射特性分析的理论基础[10-11],以求得各级次衍射效率的解。DMD 等效为二维光栅示意图如图1所示。图1 中其厚度为h,周期为d,微镜片尺寸为a。一束单色光斜入射到微镜表面,入射波矢量k1与z轴构成入射面,入射面与z轴夹角θ为光束入射角,入射面与x-o-y平面的夹角 ϕ为入射光束空间方位角。
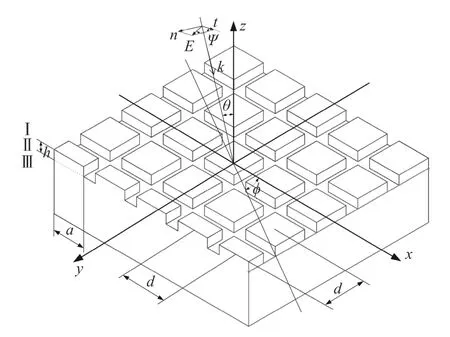
图1 DMD 等效二维光栅示意图Fig.1 Schematic diagram of DMD equivalent twodimensional grating
将DMD 微镜阵列分为3 个区域(见图1),区域Ⅰ和区域Ⅲ都是均匀介质区域,区域Ⅱ为微镜片结构区域。将微结构沿界面法向方向分为多层结构,采用RCWA 方法根据电磁波边界连续条件进行求解分析,从而实现衍射特性的求解。具体求解过程为:1)应用麦克斯韦方程组导出介质层和基底层电磁场解的表达式;2)利用傅里叶展开式推导出微分方程组;3)运用不同区域的电磁场边界条件求解各个级次的振幅和衍射效率[12-15]。
当光波以TE 模入射时,对于区域Ⅰ,入射介质层电场仅有y分量,表达式为
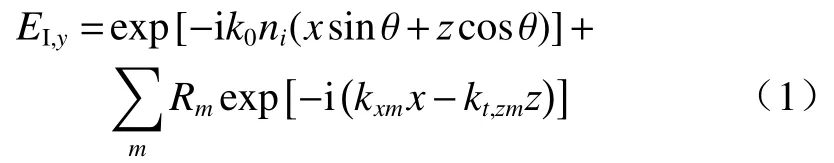
式中:Rm为反射到区域Ⅰ中的m级衍射波电场振幅;kxm及kt,zm定义为
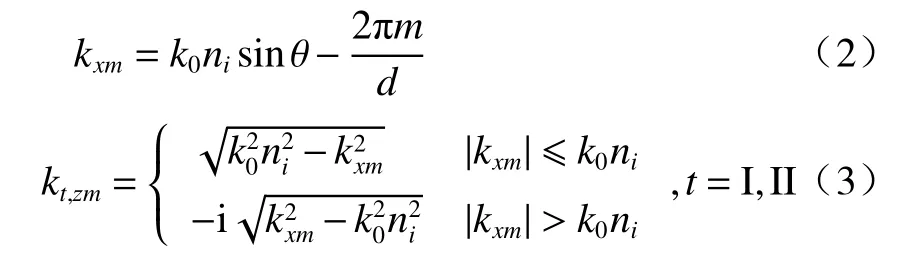
将区域Ⅱ的电磁场分量展开为傅里叶级数形式并推导出微分方程组,再根据电磁场边界条件,且边界处z=0 连续,则有

式中:ωi,m,uj,m分别为矩阵 ω和u的第m个元素;hl为第l层厚度。对于区域Ⅱ中,每一层边界处应满足

联立上述关系式,求得DMD 反射光的衍射效率 ηRm,即:
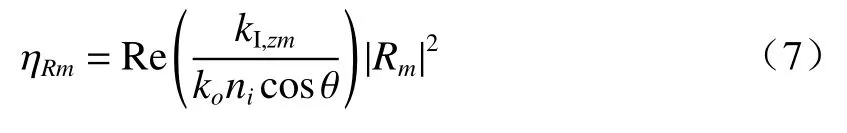
1.2 衍射特性建模
本节基于RCWA 理论对DMD 元件进行建模仿真,应用软件RSoft 中Diffract mod 进行模拟。该模块适用于分析具有周期性的微结构,因此仿真时只需对DMD 的单个微镜片建模即可,本文仿真模拟参考型号为DLP7000 的DMD。值得注意的是,当DMD 处于工作状态时,不同于简单的二维光栅,会沿着斜对角线偏转±12°,所以设置闪耀角、入射角和反射角都需要除以进行校正,仿真参数设置如表1所示。

表1 DMD 仿真参数设置Table 1 DMD simulation parameter setting
根据表1 中参数,建立单个DMD 微镜片开态结构模型,如图2所示。
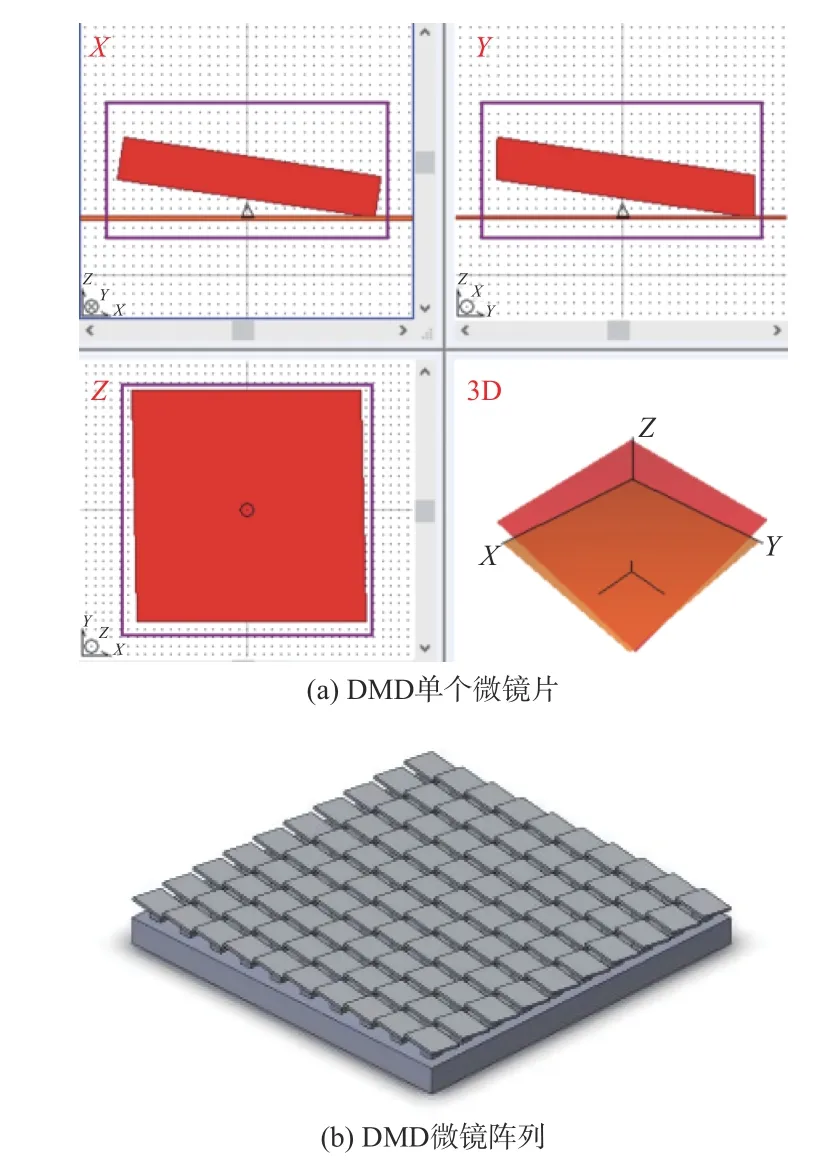
图2 DMD 微镜片模型图Fig.2 DMD micro-mirror model
2 DMD 元件衍射效应分析
2.1 不同波段对DMD衍射效应的影响
DMD 微镜尺寸与红外光波长相当,衍射效应较其他波段明显,因此本节探讨了红外波段对DMD 衍射效率的影响。针对本文分析的光学系统主光线投射到DMD 的入射角度为0°,所以利用RSoft 软件进行仿真分析时,设置入射角为0°,取步长为0.05 μm。在微镜片处于开态时,分别探讨中波红外(3 μm~6 μm)和长波红外(8 μm~12 μm)2 个波段对DMD 衍射效率的影响,得出衍射效率随波长的变化曲线,如图3所示。
从图3(a)可看出,在中波红外波段,随着波长增大,总反射光衍射效率从48%增长到64%并趋于稳定。(-1,-1)衍射级次为主工作能级,且波长为4.2 μm 时,该级次衍射效率达到峰值。其余波长下非工作级次的衍射效率略有增大,能量分布相对集中,衍射效应不是很明显。
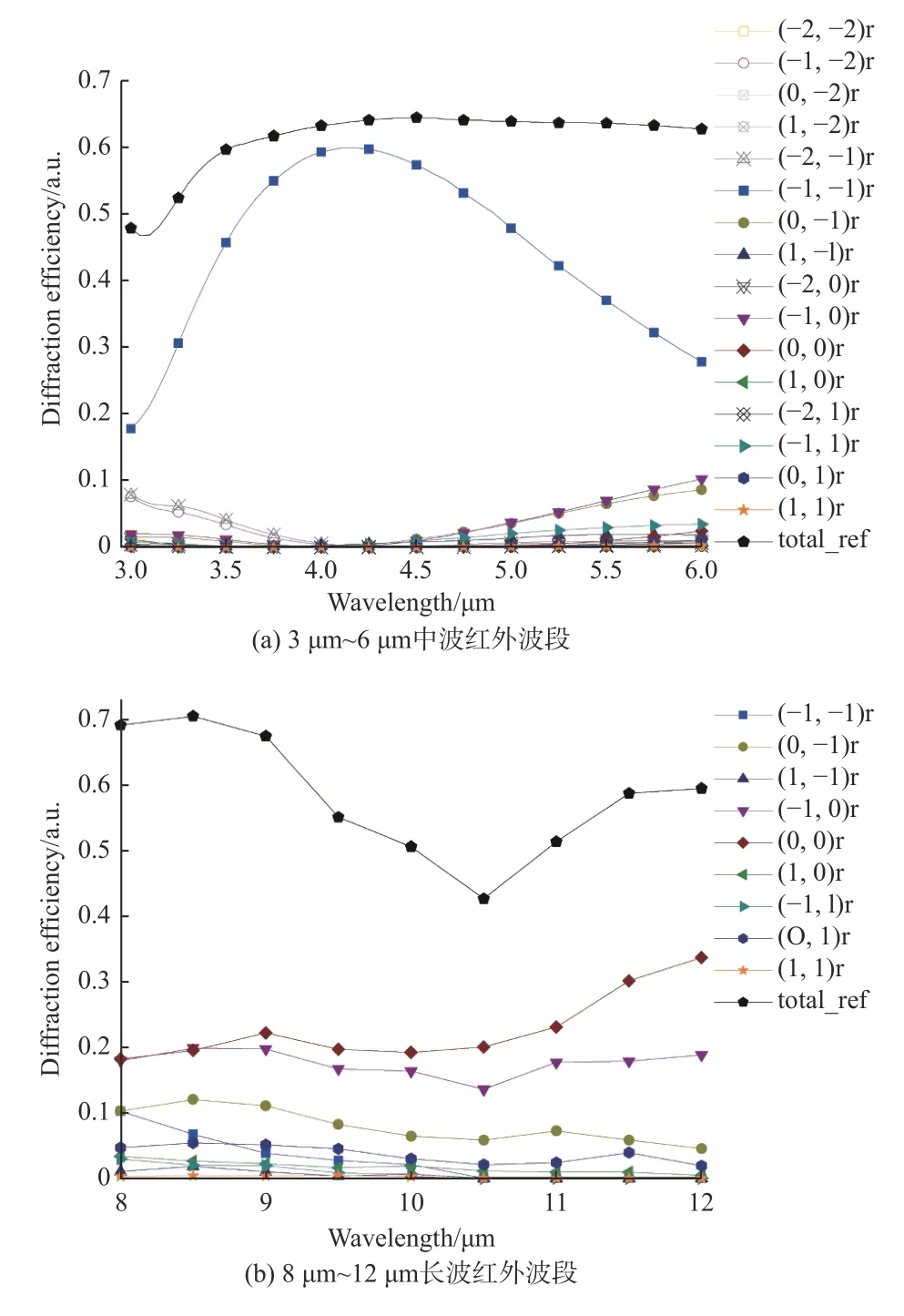
图3 不同波段衍射效率曲线图Fig.3 Curves of diffraction efficiency at different wavebands
从图3(b)可看出,在长波红外波段,总反射光衍射效率先减小,当波长为10.5 μm 时,总衍射效率呈上升趋势。(0,0)级为主工作级次,其余非工作级次能量占比较大,DMD 分光性能较强,衍射效应显著。
综合分析可知,不同波段对应不同的工作级次,短波红外波段DMD 衍射能量分布相对集中,在一些光学系统中甚至可以忽略DMD 所带来的衍射杂光影响,但对于长波红外波段,除主工作级次外,其余级次也有一定的能量占比,所带来的衍射效应会降低能量利用率,是系统杂光的主要来源。
2.2 不同入射角度对DMD衍射效应的影响
随着DMD 微镜应用日益广泛,平行光入射至微镜不再能满足光学系统性能需求,而是以一定入射角度的会聚光路入射至DMD 上。因此进一步探究入射角度在长波红外波段对DMD衍射效应的影响就非常有必要,分别取入射光波长 λ为8 μm、10 μm、12 μm,入射角度范围为0°~70°,DMD衍射光强分布变化曲线如图4所示。
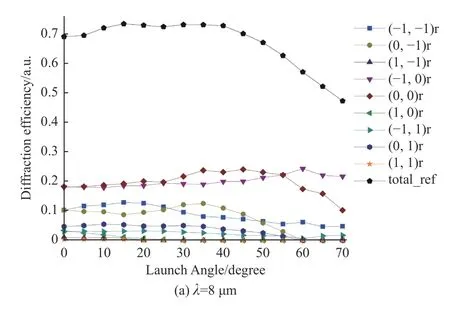
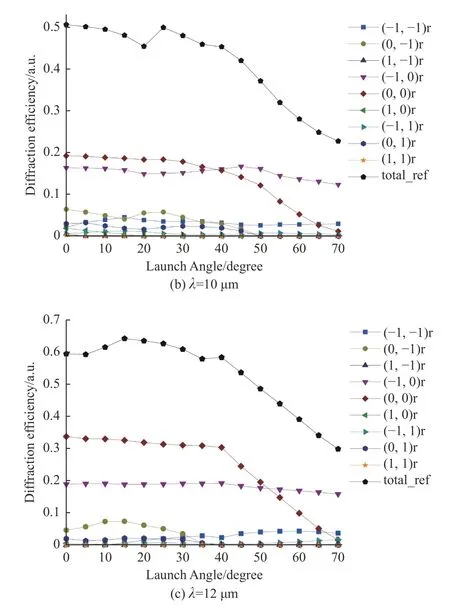
图4 不同波长下不同入射角的衍射光强分布Fig.4 Diffraction intensity distribution of different incident angles at different wavelengths
当 λ=8 μm 时,总反射衍射效率较高,但主工作级次(0,0)级能量较低,非工作级次衍射能量占比大,DMD 分光性能较强,导致探测器接收到的能量很弱。
当 λ=10 μm 时,主能级衍射能量随入射角增大呈下降趋势,其余级次能量有所增强,且当入射角大于35°时,非工作级次(-1,0)级的衍射效率过高,会产生较严重的衍射杂光。
当 λ=12 μm 时,主级次衍射能量随入射角增大而减小,其余级次能量略有上升,当入射角大于40°时,总工作级次的衍射效率骤降,同时(0,0)级也呈明显下降趋势。
综上所述,在长波红外波段,当波长小于10 μm时,(0,0)级衍射效率较小,DMD衍射效应较大。在波长为10 μm~12 μm 范围内,通过控制入射角度可使主工作级次获得较高的衍射能量,且适当减小入射角度可以减少DMD衍射效应。
3 结合DMD 的光学系统杂光分析
为验证上述结论的准确性,进一步分析投影系统中DMD衍射效应对杂散光的影响,设置光源波长为8 μm、10 μm、12 μm,并通过在Lighttools软件中设置不同光源发散角来控制系统F数,进而控制入射至DMD 的角度。这是由于投影光学系统的像面相对于系统整体尺寸比较小,系统的视场相对不大,因此入射到DMD 上的角度主要由其像方数值孔径即F数决定。为了重点分析DMD衍射效应引起的杂光,将透镜及结构件散射表面设为近似理想情况。设置透镜表面透过率为99.95%,反射率为0.05%,结构件内表面吸收率设为98%,散射率为2%,同时采用朗伯散射模型。光源能量设置为5 W,光线阈值为10-7,并设置光线数目为25×104条,对系统进行光线追迹,如图5所示。

图5 DMD 光学系统光线追迹图Fig.5 Ray tracing diagram of DMD optical system
经光线追迹后,发现当F数过小时,经DMD调制后的部分光路会反射至透镜边缘无法到达探测器表面;当F数较大时,像面处探测器能量较低,降低了系统成像质量。因此限定系统F数范围为3~10,对应边缘入射角度为8°~3°,在此限定范围基础上,计算DMD 衍射杂光能量占比,并以照度分析图作为衍射杂光评价方式。当波长为10 μm,系统F#=6 时,对DMD 设置不同的光学属性的探测器表面照度图如图6所示。图6(a)为将DMD 主工作级次能量设置为0,其余级次由前文计算得到的能量分布的表面照度图;图6(b)为DMD 光学属性直接由RSoft 软件生成的表面散射模型的表面照度图;图6(c)为将DMD 等效为平面反射镜的表面照度图。
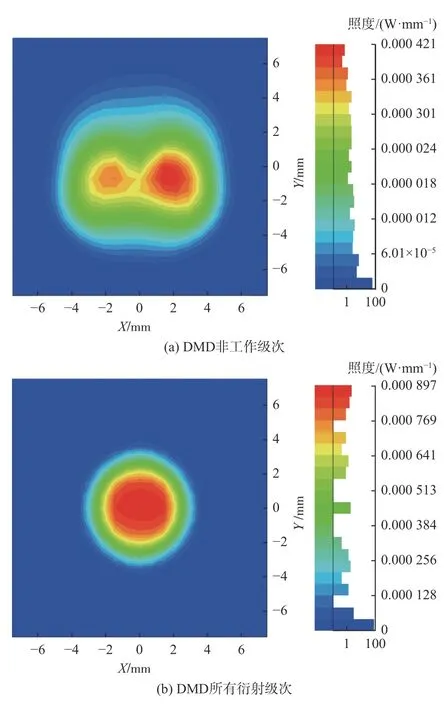
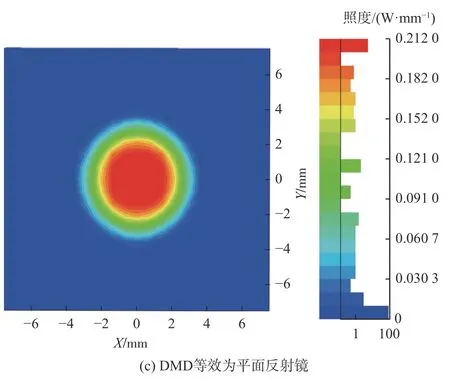
图6 探测器表面照度图Fig.6 Illumination diagram of detector surface
由图6(a)可看出,DMD 衍射杂光光斑图中右侧能量较大的光斑主要为(-1,0)级次的衍射杂光,经DMD 调制后非工作级次的光会造成一定的能量损失,同时降低了系统成像质量,探测器接收总能量照度为0.026 12 W/mm2。由图6(b)可看出,DMD 所有衍射级次的照度图中光斑较为均匀,但在光斑边缘处,仍可看到非工作级次杂光的存在。由图6(c)可看出,将DMD 等效为平面反射镜后相较图(b)能量更集中均匀,探测器接收总能量照度为4.981 26 W/mm2。
本文定义DMD 非工作级次衍射能级照度与DMD 等效为平面反射镜的照度之比为衍射杂光能量占比。因此,计算出不同波长下不同F数时系统衍射杂光能量占比变化曲线,如图7所示。
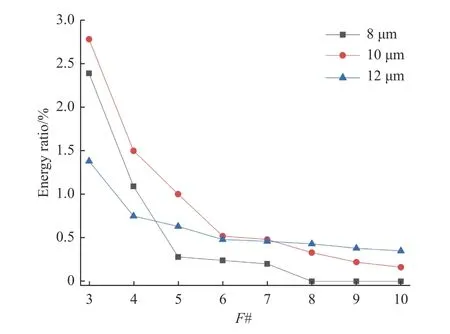
图7 不同波长下不同F 数系统衍射杂光能量占比曲线Fig.7 Energy proportion curves of diffracted stray light of different F number at different wavelengths
由图7 可知,当波长为8 μm 时,光束经DMD调制后只有少部分进入会聚系统到达探测器表面,甚至在F数为8~10 时,探测器上无衍射级次能量。在波长为10 μm~12 μm 波段,F数越大,即入射角度越小,DMD 衍射杂光能量占比越小。
4 结论
基于RCWA 理论构建了DMD 的衍射模型,探讨了不同波段不同入射角度对DMD 衍射特性的影响,并分析了DMD 应用在投影系统时,产生的衍射效应对系统杂散光的影响。研究结果表明,长波红外波段DMD衍射效应更明显,且随着入射角度增大,DMD 分光性能随之增大,衍射效应显著。最后给出长波红外波段,不同F数系统杂光随DMD 衍射变化曲线,F数越大,DMD衍射效应对系统杂光影响越小。该结论相较于已有的研究工作,更详细分析了DMD 的衍射杂光对系统的影响,为具有DMD 的复杂光学系统设计奠定了基础,并对包含衍射元件的光学系统杂散光分析提供了新的思路。
