基于模态参数及BAS-PSO优化算法的软基水闸有限元模型参数修正方法
2021-09-23李火坤魏博文黄锦林
李火坤,王 刚,余 杰,魏博文,黄 伟,黄锦林
(1. 南昌大学建筑工程学院,南昌 330031;2. 广东省水利水电科学研究院,广州 510610)
据统计,中国建成的流量超5 m3/s及以上的水闸达103 878座[1],其在防洪、灌溉、航运等方面发挥着不可替代的作用。然而,复杂的服役环境和水流的常年侵蚀给长期服役的水闸带来不同程度的安全隐患,尤其是坐落于软基上的水闸(软基水闸),易出现闸室不稳定、结构损伤、闸基渗流破坏、底板脱空等问题[2 − 4],严重影响水闸工作效能的发挥。因此,水闸结构健康监测及性能评估研究对于保证水闸的长期安全运行具有重大意义。准确可靠的有限元模型是结构健康监测的基础[5 − 6],但由于模型参数的不确定性,使得建立的有限元模型不能准确地反映水闸结构真实的动力学特性,进而影响水闸损伤识别和性态评估的精度。当前,基于实测信息的水闸有限元模型参数修正方法是一种比较可靠的方法。
在工程结构领域中,有关有限元模型参数修正方法按实测信息可分为基于静力信息的有限元模型参数修正方法和基于模态参数的有限元模型参数修正方法。近年来,随着测试技术和系统辨识理论的蓬勃发展,基于模态参数的有限元模型修正方法发展迅速,克服了静力信息难以在线监测的局限性,引起了诸多学者的广泛关注。李晰等[7]采用FDD法识别出实际结构的模态参数,以此结合零阶近似法来修正钢管混凝土连续梁拱桥有限元模型;Chen等[8]提出了基于不完整模态数据的更新有限元动力学模型方法,通过建立结构修正参数与模态数据之间的精确关系,采用迭代求解法来确定结构参数;Girardi等[9]提出了基于欧几里德范数中测量频率和计算频率的最小值来修正有限元模型;Hofmeister等[10]提出了以有限元模型振型MAC计算值与实测值之间的误差最小来构建有限元模型修正的目标函数;Kang等[11]提出了基于频率计算值和实测值之间相对误差的目标函数来修正有限元模型参数,通过改进的人工鱼群算法实现了优化求解。选择合理可靠的智能算法对水闸有限元模型参数修正尤为重要。目前,已有诸多算法应用于有限元模型参数修正,如遗传算法(GA)[12]、粒子群算法(PSO)[13]、乌鸦搜索算法[14]及改进算法[15 − 17]等,但由于许多智能算法存在一定的局限性,如群体算法存在计算效率较低的问题,个体算法存在难以实现全局收敛的问题等,有待进一步改进。
为此,本文结合模态参数和基于天牛须搜索算法的粒子群(BAS-PSO)优化算法,提出一种软基水闸有限元模型参数修正方法。首先,将改进的变分模态分解法(IVMD)和随机子空间法(SSI)相结合,提出精确识别水闸振动模态参数的IVMDSSI法;其次,基于支持向量回归(SVR)原理,建立表征软基水闸待修正参数和模态参数之间非线性关系的GA-SVR代理模型;构建软基水闸有限元参数修正的目标函数,并提出一种BAS-PSO优化算法进行优化求解;最后,将本文方法应用于软基水闸物理模型,验证方法的有效性。
1 软基水闸有限元模型参数修正
1.1 基于IVMD-SSI的软基水闸振动模态参数识别
为精确地挖掘软基水闸振动响应信号中含有的振动模态参数,提出IVMD-SSI法来开展软基水闸振动模态参数识别。首先,基于IVMD方法对水闸振动响应信号进行降噪处理,将噪声信号从水闸振动信号中分离并滤除,保留信号中结构工作特征信息;随后,利用SSI法对降噪后的信号进行识别,得到水闸振动模态参数。
1.1.1 软基水闸振动响应信号的降噪处理
变分模态分解(VMD)作为一种多分量自适应信号分解方法,能够通过求解约束变分问题来将振动信号f分解成K个有限带宽的本征模态函数(IMF),从而实现降噪处理。约束变分问题描述如下:
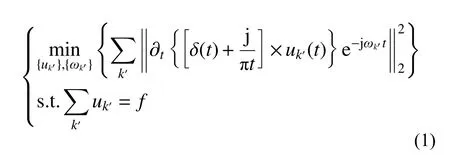
式 中: δ(t) 为 狄 拉 克 分 布;uk′(t) 为 第k′个IMF;j为复数单位;ωk′(t) 为第k′个IMF的中心频率。为求解上述变分约束模型,引入二次惩罚因子和Langrange乘法算子使得变分约束模型转换成非约束变分问题,则有:

式中: α是二次惩罚因子;λ(t)是Langrange乘法算子。通过交替方向乘子算法在频域内求解式(2),计算增广Langrange函数的鞍点,即式(1)的最优解,并不断地迭代更新和优化uk′、ωk′和λ,从而实现信号分解。
然而,传统的VMD算法进行降噪时需预设K值,而K值的选取直接影响到信号分解的准确性。为避免K值不确定性所带来的偏差,利用互信息法来改进VMD算法以实现K值的自适应选取,表达式如下:

式中:I(XI,YI) 为IMF分量XI和YI的互信息系数;H′(XI) 和H′(YI) 分别为IMF分量XI和YI的熵;H′(XIYI) 为IMF分量XI和YI的联合熵。计算各IMF分量的归一化互信息系数(NMIC),并设定NMIC阈值[18]为0.02,当分量分解至NMIC小于阈值时,表明该分量与原信号不相关,此时信号已分解充分,由此自适应确定K值。
1.1.2 软基水闸振动模态参数的识别
SSI是一种通过建立随机状态离散空间模型来识别结构模态参数的方法,其基本原理如下:
对于有N个测点,且每个测点数据长度为l,可将IVMD降噪输出的测点响应数据组成2Nc×l的分块Hankel矩阵:

式中,Y0|c−1为Hankle矩阵中第1行的下标起始时刻为0、终点时刻为c−1的所有测点组成的Hankle矩阵的块。根据统计序列原理,当l/c足够大时,可以认为l→∞,把Hankel矩阵的行空间分成“过去”行空间和“将来”行空间,并对Hankle矩阵进行QR分解:

由系统矩阵A1和输出矩阵C1可识别出软基水闸振动模态参数。
1.2 GA-SVR代理模型
本文从材料参数的角度出发,选择对水闸结构模态参数影响较大的弹性模量E和密度 ρ[19 − 20]作为待修正参数x={E,ρ},构建表征软基水闸待修正参数和模态参数之间的非线性数学关系的GA-SVR代理模型,其基本思路如下:采用拉丁超立方抽样法(LHS)[21]生成较小的待修正参数样本集,将其输入有限元模型并得到相应的模态参数集,依据非线性映射原理将参数输入空间映射至高维空间,利用线性可回归的超平面来拟合软基水闸待修正参数和模态参数之间的非线性数学关系,并利用遗传算法优化求解模型中的正则化参数C和核函数参数g,从而建立表征软基水闸待修正参数和模态参数之间的非线性数学关系的GA-SVR代理模型。其中,SVR的基本原理如下:

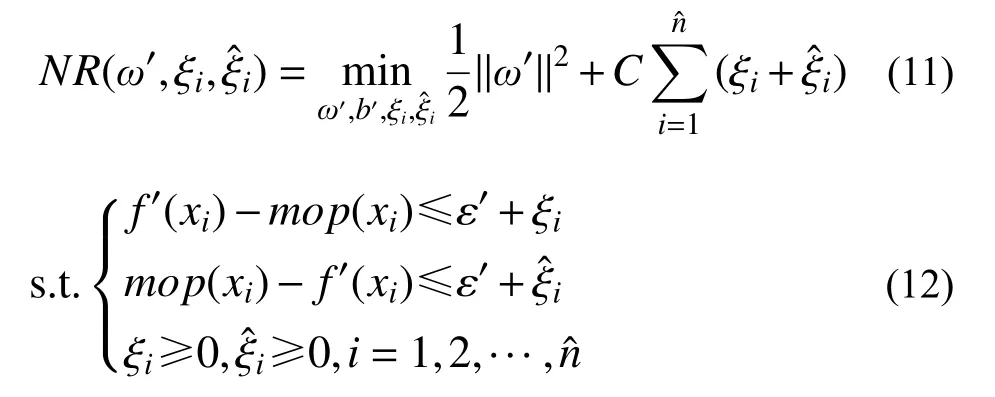
式中,C为正则化参数。通过引入Lagrange乘子,得到拉格朗日函数,依据优化条件,SVR的对偶问题可转化为如下问题:
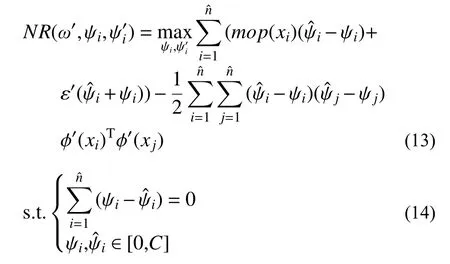
本文采用径向基函数作为SVR的核函数,SVR的回归方程如下:
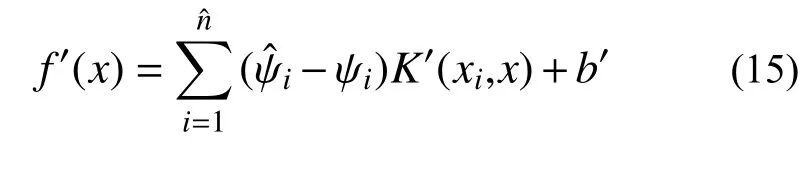
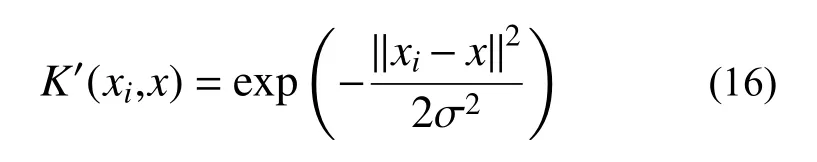
式中, σ 为径向基核函数的宽度参数。
1.3 软基水闸有限元模型参数修正的目标函数
以软基水闸振动模态参数与GA-SVR代理模型计算模态参数之间的相对偏差最小来构建目标函数,则目标函数可表示为:
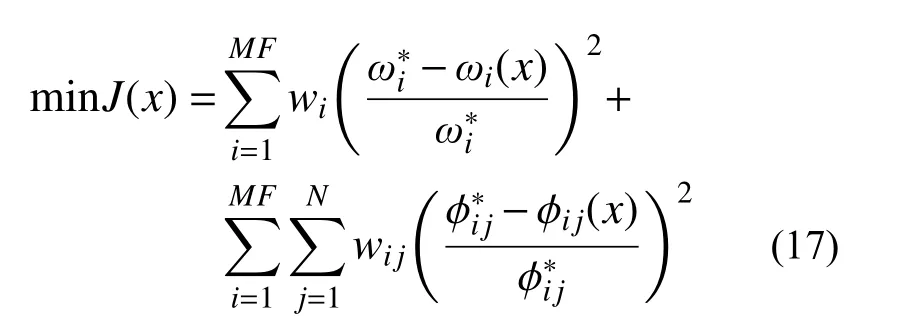
1.4 BAS-PSO优化算法
天牛须搜索(BAS)算法是由Jiang等[24]提出的个体寻优算法,具有收敛速度快、效率高的特点,但对于多目标函数寻优求解时,受个体的局限性难以考虑多变量之间的相关性。PSO算法作为群体寻优算法,具有良好的全局收敛能力,并且能够有效地克服个体寻优的局限性,但传统的粒子群算法计算效率较低,难以满足要求。为此,本文将BAS算法和PSO算法相结合,提出一种BAS-PSO优化算法,该算法不仅考虑了变量之间的相互作用,还提高了优化求解的效率,其基本思路是将粒子群中个体视作天牛个体,基于BAS算法确定个体最优适应度值,基于PSO算法更新群体,以此搜寻最优解。BAS-PSO优化算法的基本原理如下:

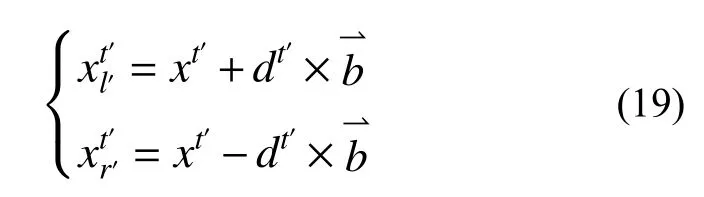





BAS-PSO优化算法基本步骤如下:1)采用MATLAB编程软件,随机生成大小为200的粒子种群,定义最大迭代数为25,初始学习c1和c2分别为1.5和1.7,并确定适应度函数;2)将种群粒子视作天牛个体,定义两须之间的距离为0.04,迭代步长的取值范围为[0, 0.2],采用BAS算法计算当代种群粒子的适应度值,确定天牛个体最优位置,并更新个体最优解和局部最优解;3)采用PSO算法对粒子群的位置和速度进行迭代更新,并重复步骤2),计算更新后种群的最优解;4)当算法达到迭代次数25或者gbest小于10−6时,则停止搜索并输出最优解,否则将继续重复步骤3),直至搜索到满足收敛准则的值为止。
1.5 软基水闸有限元模型参数修正流程图
基于模态参数及BAS-PSO优化算法的软基水闸有限元模型参数修正方法流程图如图1所示。

图1 软基水闸有限元模型参数修正流程图Fig.1 Flow chart of parameter updating of finite element model of sluice on soft foundation
2 软基水闸物理模型实例
2.1 软基水闸物理模型基本情况
以某一原型软基水闸工程为背景实例,制作比尺为1∶10的单孔软基水闸物理模型,其示意图如图2所示。水闸结构采用钢筋混凝土浇筑,软基采用细沙、砾石及黏土填充,软基四周设置混凝土边墙约束,软基水闸物理模型如图3所示,其基本尺寸如下:水闸长为1.44 m、宽为1.36 m、高为1.6 m,底板厚为0.16 m,闸墩厚为0.16 m,前后工作桥宽分别为0.32 m和0.4 m,工作桥厚为0.04 m,软基长为3.04 m、宽为2.96 m,地基高为0.54 m。本文对软基水闸物理模型开展了人工脉冲激励下的振动响应测试,将径向加速度传感器对称布置于水闸左右两侧。在右侧闸墩顶部从左至右布置4个测点,编号为B1~B4;在B4号测点处自上而下布置6个测点,编号为B5~B10,传感器布置情况如图4所示。传感器采用BY-S07高精度振动传感器,如图5所示,振动测试时采用速度档,测试频响范围为1 Hz~100 Hz。本文在两次不同的人工激励下开展振动测试,以此作为计算工况和验证工况。
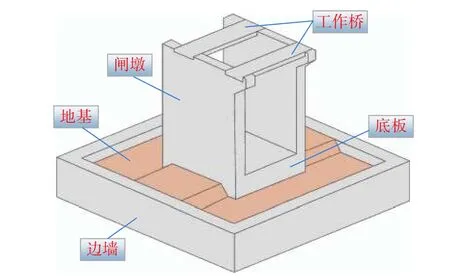
图2 软基水闸模型示意图Fig.2 Schematic diagram of sluice

图3 软基水闸物理模型Fig.3 Physical model of sluice
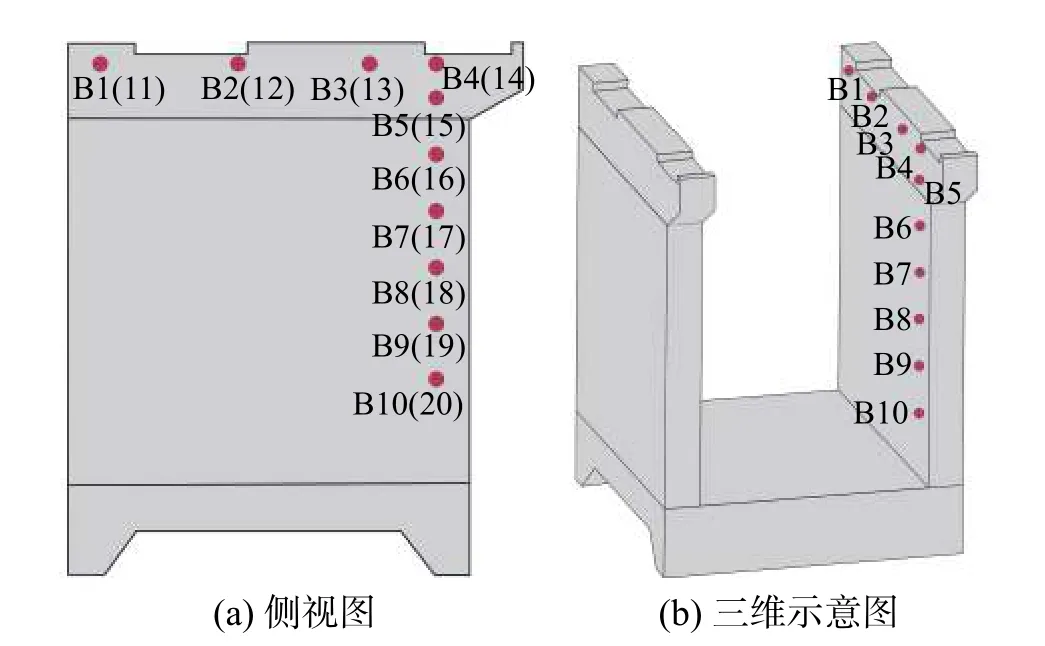
图4 传感器布置图Fig.4 Sensor arrangement

图5 BY-S07传感器Fig.5 BY-S07 sensor
2.2 软基水闸振动模态参数辨识
以计算工况为例,采用IVMD法对典型测点(B7)进行信号分解,利用互信息法确定模态数为4,经过IVMD分解得到的4个信号分量时程线(如图6所示),其NMIC值如表1所示,可知,各个信号分量的NMIC值均大于阈值0.02,满足分解要求。将典型测点信号分量进行重构,得到B7测点降噪前后时程线和功率谱密度曲线(如图7和图8所示),由图8可知,原始信号中的低频噪声得到了有效地剔除。采用SSI法对降噪后的信号进行模态识别,得到软基水闸振动模态参数,如表2所示,其中,水闸前四阶固有频率分别为20.43 Hz、24.78 Hz、60.85 Hz和70.41 Hz,第一阶振型为同向振动,第二阶振型为反向振动,第三阶振型为同向扭动,第四阶振型为反向扭动,且各阶阻尼比均在3.11%以内。
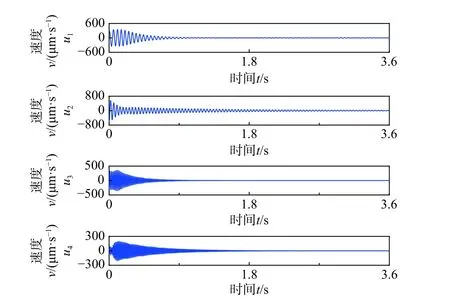
图6 B7测点信号分量时程线Fig.6 Time history of signal components of B7

表1 B7测点信号分量的NMIC值Table 1 NMIC of signal components of B7
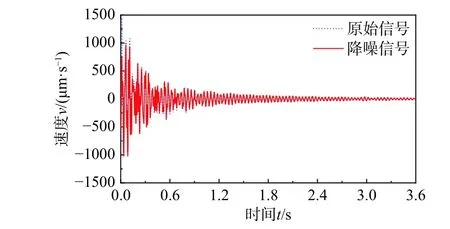
图7 B7测点降噪前后时程线Fig.7 Time history before and after de-noising of B7
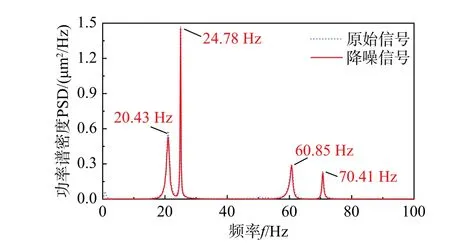
图8 B7测点降噪前后功率谱密度曲线Fig.8 Power spectrums before and after de-noising of B7
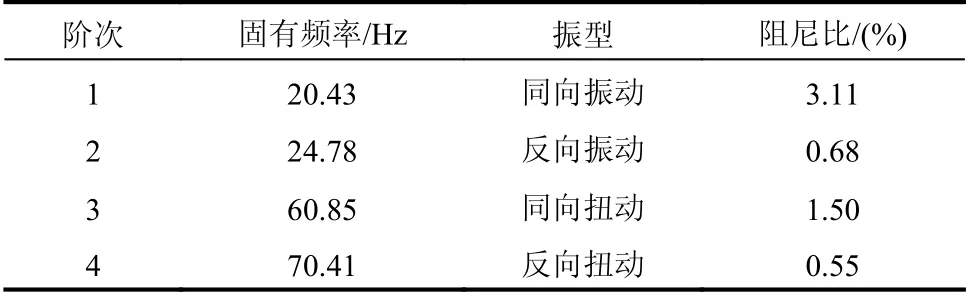
表2 水闸振动模态参数识别结果Table 2 Modal parameter identification results of sluice
2.3 软基水闸有限元模型
由于水闸钢筋布置和混凝土养护存在差异,且地基不同区域的填充材料和压实度不同,导致其弹性模量和密度不同。因此,可将水闸分为底板A、左闸墩B、右闸墩C和工作桥D四个区域,地基分为上层E、中层F和下层G三个区域。运用ANSYS有限元软件建立软基水闸有限元模型,如图9所示,地基四周及底部采用法向约束来模拟地基边墙的作用,工作桥与闸墩的连接方式采用搭接,有限元模型共划分有91 602个单元和106 150个节点。

图9 软基水闸有限元模型Fig.9 Finite element model of sluice
2.4 支持向量机代理模型的建立
对水闸工作桥D的弹性模量和密度进行检测,得到其弹性模量和密度分别为19.04 GPa和2512 kg/m3,并以此作为参考来确定水闸其他区域弹性模量和密度的取值范围;根据文献[25],确定地基弹性模量和密度的取值范围,如表3所示。采用LHS法在弹性模量和密度的取值范围内随机生成750组样本数据,并将其输入有限元模型进行模态计算,得到的750组频率和归一化振型系数,其中700组数据作为样本集,50组数据作为测试集。设置模型的初始参数如下:初始种群大小为200,最大代数为25,交叉率为0.9,变异率为0.1,C的取值范围为[0.1, 100],g的取值范围为[0.1, 1000]。使用GA算法搜索模型中最优的正则化参数C和核函数参数g,并建立相应的GASVR代理模型。以频率和典型测点为例,引入均方误差(MSE)、平均绝对百分误差(MAPE)、相关系数(R2)作为评价指标来量化GA-SVR代理模型的拟合精度,结果如表4和表5所示。

表3 弹性模量和密度取值范围Table 3 Ranges of elastic modulus and density

表4 频率评价指标Table 4 Evaluation index of frequency

表5 典型测点归一化振型系数评价指标Table 5 Evaluation index of mode shape normalized coefficients of type measuring point
2.5 BAS-PSO优化算法求解
基于式(17)建立最优化数学模型,采用BASPSO优化算法对其进行优化求解,得到软基水闸各分区弹性模量和密度,结果如表6所示。同时与自适应惯性权重的PSO算法(AWPSO)[26]和BAS算法进行对比,如图10所示;可知,BAS-PSO优化算法在第12代时收敛,而AWPSO算法和BAS算法分别在第16代和第14代收敛,且BAS-PSO优化算法计算的适应度值更小,表明该算法具有更快的收敛效率和更高的精度。

图10 优化算法对比Fig.10 Comparison of optimization algorithms

表6 模型参数修正计算结果Table 6 Calculation results of model updated parameters
2.6 结果验证
为验证该方法的准确性,将弹性模量和密度的修正结果输入有限元模型,得到频率对比结果(如表7所示)和振型对比结果(如表8和图11所示)。从对比结果来看,对于频率而言,最大相对误差为−4.75%,表明修正后参数计算所得的频率与模态识别的频率在数值上比较吻合;对于测点归一化振型系数而言,大部分测点在数值和规律上都吻合较好,其识别值与计算值之间的相对误差都在12.73%以内,仅有三个测点归一化振型系数稍大,即第一阶B10测点的相对误差为−16.95%,第二阶B20测点的相对误差为22.93%,第四阶B19测点相对误差为−14.38%,主要是由于位于闸墩底部的测点振动幅值较小,受噪声干扰大,导致振型识别产生一定的偏差。总体而言,基于修正后参数的软基水闸计算模态参数与软基水闸振动模态参数吻合较好,该方法是合理可靠的。

图11 振型对比结果Fig.11 Comparison of mode shape

表7 频率对比结果Table 7 Comparison of frequency

表8 测点归一化振型系数对比结果Table 8 Comparison of mode shape normalized coefficients of measuring points
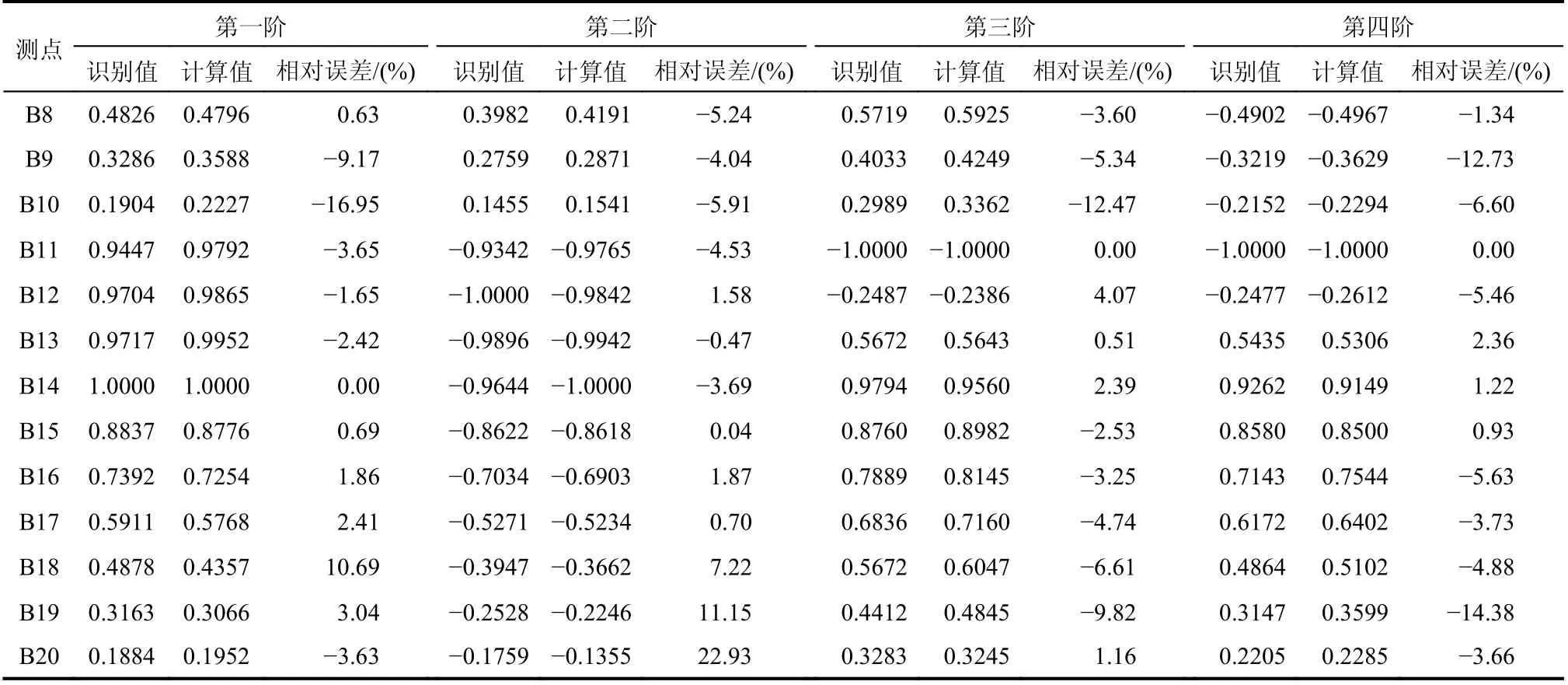
续表8
3 结论
本文提出了一种基于模态参数及BAS-PSO优化算法的软基水闸有限元模型参数修正方法,主要结论如下:
(1) 基于软基水闸振动响应信号,提出了IVMDSSI法来识别软基水闸振动模态参数,避免了VMD算法中参数不确定性所产生的偏差,有效地剔除了信号中的噪声成分,并极大地提高了水闸振动模态参数的识别精度。
(2) 选择对水闸模态参数影响较大的弹性模量和密度作为待修正参数,建立了反映软基水闸待修正参数与模态参数之间非线性关系的GA-SVR代理模型,大大减少了有限元正分析的计算量,提高了参数修正的计算效率和计算精度。
(3) 提出了基于GA-SVR代理模型计算模态参数与水闸振动模态参数之间相对偏差最小的目标函数,构建了软基水闸有限元模型参数修正的最优化数学模型,将有限元模型参数修正问题转换为目标函数优化求解问题。
(4) 提出了一种BAS-PSO优化算法,既保留了BAS算法的高收敛速度和PSO算法的高收敛精度,又克服了BAS算法难以考虑变量之间的相互作用的问题。经过工程实例验证表明,本文方法合理可靠且具有良好的可行性,可为软基水闸有限元模型参数修正提供一条新思路。
