基于简化四阶矩法的各种截面钢管混凝土轴压承载力可靠度分析
2021-09-23丁发兴熊姝宁
丁发兴,熊姝宁,向 平
(1. 中南大学土木工程学院,湖南,长沙 410075;2. 湖南省装配式建筑工程技术研究中心,湖南,长沙 410075)
现代建筑具有高层,大跨等特点,对柱的承载力要求高,而钢管混凝土短柱(CFST)具有刚度大、承载力高、延性好和充分利用材料等优点,在实际结构中得到了广泛的应用。钢管混凝土短柱能否在设计使用年限内完成其在设计阶段的预定功能,需要对其进行可靠度评估。
可靠度理论从20世纪40年代发展起来,其主要的用途是评估各种结构和系统在加工以及使用阶段完成预备功能的能力。结构可靠度理论经历了第一代和第二代结构设计理论[1],第二代结构设计理论采用基于矩法的可靠度理论,用统计矩反映荷载和抗力分布,进而得出结构的失效概率Pf及其相应的可靠指标β,如一次二阶矩理论(FOSM)使用变量的前两阶矩,即均值和方差,该方法具有计算简便且表达公式简洁的特点,因此在工程中得到广泛应用,如吴瑾等[2]采用一次二阶矩法评估锈蚀钢筋混凝土结构可靠度。林道锦等[3]为了计算钢筋混凝土拱桥面稳定性的剩余可靠度,提出一次可靠度方法与随机有限元相结合的方法。党育等[4]结合有限元方法和一次二阶矩法,对隔震体系进行模拟并分析其抗震可靠度。Mahdi Omidali等[5]采用FOSM对边坡、船舶加筋板、桩和钢筋混凝土桥柱等结构进行可靠度分析。由于FOSM将函数展开成Taylor级数并取至一次项,故当函数非线性程度较高时难以反映变量真实的概率分布特征,为了提高FOSM的精度,学者们提出改进的一次二阶矩法,如吕大刚等[6]在FORM的基础上引入多级力控制 Pushover 分析方法,提出了一种FORM有限元可靠度方法。孟增等[7]提出了一种结合了修正的混沌控制算法与一次二阶矩法的方法。蒋水华等[8]提出基于FORM的空间变异边坡可靠度方法以及线抽样法进行了边坡可靠性评估。
一次四阶矩法采用功能函数的前四阶矩进行可靠度分析,结果的精度与一次二阶矩法相比大大提高,因此学者们运用高阶矩法评估结构的可靠性,如Li等[9]基于二次二阶矩(SOSM)、二次四阶矩(SOFM)和蒙特卡洛模拟(MCS)方法,评估了风桥相互作用相关的各种参数对涡激振动器的影响,邹红等[10]用矩法对CRTSⅡ型无砟轨道板横向抗弯强度进行时变可靠性评估。一次四阶矩法对于非线性程度较高的功能函数,其计算精度较低,学者们在此基础上提出了一些改进方法,如Li等[11]、Lu等[12]和Zhou等[13]分别提出了基于三阶矩、四阶矩和六阶矩的鞍点近似法。俞登科等[14]利用矩法,对特高压输电塔的抗风体系进行可靠度分析。范文亮等[15]提出了一种适用于岩土工程的改进四阶矩方法,并进行算例验证。杜永峰等[16]建立了基于二次四阶矩可靠度理论的随机鲁棒性指标,并对隔震结构的抗倒塌能力进行了评判。
近年来,丁发兴课题组[17 − 24]提出了各截面钢管混凝土轴压承载力公式,且目前的研究工作主要集中在对圆形和方形钢管混凝土轴压承载力进行可靠度评估,而对于其他截面形式,可靠度尚未开展评估,为此笔者主要工作如下:1)收集国内外学者进行的各种截面钢管混凝土短柱轴压承载力实验数据,获取基本随机变量的统计参数并建立构件的功能函数;2)运用新点估计法计算功能函数的前四阶中心矩;3)利用简化四阶矩法计算各种截面钢管混凝土轴压承载力公式可靠指标β。
1 基本随机变量的统计参数
功能函数的基本随机变量包括抗力、恒荷载和活荷载。抗力的分布由多个基本随机变量影响,包括混凝土轴心抗压强度fc,截面尺寸D和B,钢管厚度t,钢材屈服强度fy,计算模式不定性系数kp。抗力的分布近似服从对数正态分布[25]。
1.1 轴压承载力公式
钢管混凝土轴压承载力公式为:

式中:R为根据公式计算出来的钢管混凝土轴压极限承载力;fc为混凝土轴心抗压强度;fy为钢管的屈服强度;Ac为钢管内核心混凝土的面积;As为钢管的横截面积;k1为钢管形状约束系数,与截面形状有关,表1给出了式(1)中不同形状的截面所对应的k1[17 − 24]取值。表2列出了不同形状截面的计算公式[17 − 24]。

表1 钢管形状约束系数k1列表Table 1 Shape confinement coefficient of CFST

表2 不同截面钢管混凝土柱Ac和As的计算公式Table 2 Calculation formula of Ac and As for concrete filled steel tubular columns with different sections
荷载效应S[26]表达式如下:

式中:SGk为恒荷载效应标准值;SQk为活荷载效应标准值,仅考虑办公室楼面活荷载和住宅楼面活荷载;γG为恒荷载分项系数;γQ为活荷载分项系数。

图1 各种截面钢管混凝土Fig.1 Sections of different shapes
由式(1)与式(2)可得钢管混凝土轴压极限状态Z的方程为:

式中,kp为钢管混凝土轴压抗力计算模式不定性的随机变量。
1.2 荷载的统计参数
最常见的荷载效应组合有两种:1)SG+SL办和2)SG+SL住,下标G、L办、L住分别代表永久荷载、办公室活荷载和住宅建筑的楼盖活荷载,恒载和活载组合时的统计参数见表3。

表3 荷载组合时的荷载统计参数[27]Table 3 The statistical parameters of load combinations
1.3 几何尺寸的统计参数
普通钢管混凝土的几何参数有钢管厚度t、截面直径或厚度D以及截面长边边长B,均服从均值系数为1.00,变异系数为0.05的正态分布[27]。
1.4 计算模式不定性的统计参数
反映构件计算抗力与实际抗力差异的计算模式不定性随机变量kp表达式如下:

式中:Nu为构件轴压承载力实测值;N0为按式(1)计算的构件抗力值。
根据《混凝土结构设计规范》(GB 50010−2010)[26]规定,立方体抗压强度标准值fcu,k与轴心抗压强度标准值fck的关系如下:
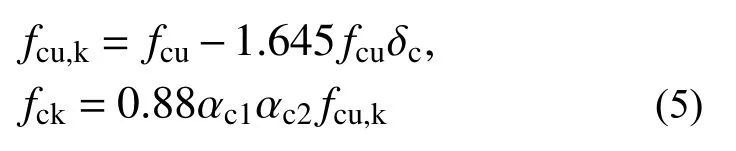
式中,对于不超过C50级的混凝土,取αc1=0.76,对C80取αc1=0.82,中间按线性规律变化,大于C80的混凝土,按C50~C80的线性规律继续插值;对C40以下混凝土取αc2=1.0,对C80取αc2=0.87,中间按线性规律变化,大于C80的混凝土,按C40到C80的线性规律继续插值;混凝土强度的变异系数δc的取值按表4确定。

表4 混凝土强度的变异系数[26] /(%)Table 4 Variation coefficient of concrete strength
笔者收集了国内外460个圆形、340个矩形、16个六边形、30个八边形、71个椭圆形和29个圆端形截面钢管混凝土短柱轴压承载力实验数据[17 − 23, 28 − 77],其 中 包 括 本 书 中 提 到 的37个 圆形、20个矩形、8个六边形、8个八边形、8个椭圆形和26个圆端形截面钢管混凝土实验数据。所有946个数据的钢管外截面尺寸与厚度比值在20~220,构件长厚比L/B(或L/D)≤7,立方体抗压强度fcu在25 MPa~120 MPa,钢管的屈服强度fy在180 MPa~650 MPa。
将各随机变量的取值代入式(1),得到Nu,再利用式(4)求得kp,各截面钢管混凝土的计算模式不定性系数kp统计结果见表5,并对每个kp的概率分布进行Jarque-Bera检验,显著性水平为5%,结果表明kp服从正态分布。
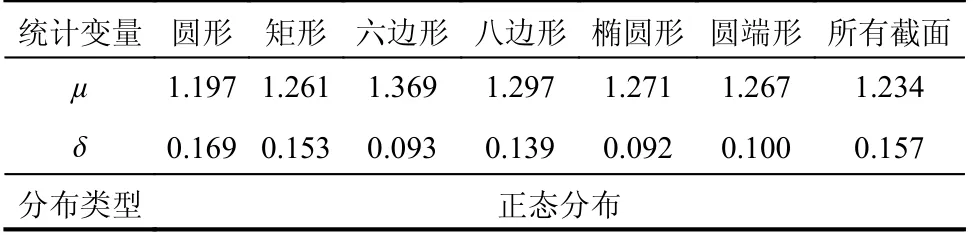
表5 普通钢管混凝土轴压公式计算模式不定性统计参数Table 5 The statistical parameters of calculation model uncertainty
1.5 材料性能的统计参数
由于规范中只给出了C60以下混凝土材料性能的变异系数,故笔者利用文献[78]给出的演绎法推算混凝土材料性能的均值系数和方差,钢材材料性能的均值系数和方差见文献[78],钢材和混凝土性能的统计参数见表6。
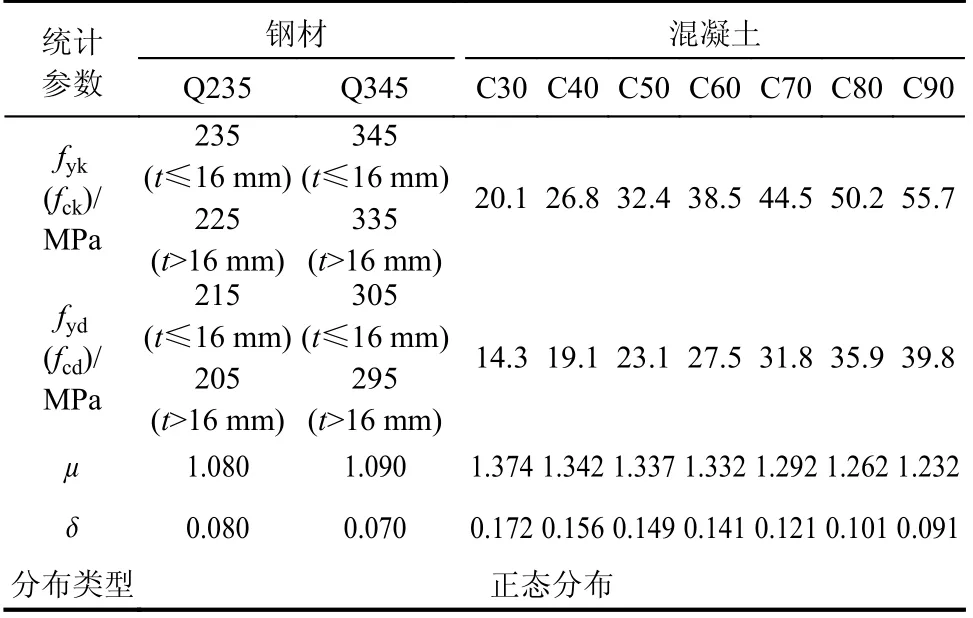
表6 材料性能指标的统计参数[25- 26, 78]Table 6 The statistical parameters of material
2 可靠度方法
2.1 基于降维模型的新点估计法
对于含有n个随机变量的功能函数G(X),Zhao等[79]提出了基于n点估计的一维减维模型:

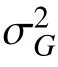
一维减维模型将功能函数化为n个单变量函数而简化了计算过程,但当功能函数有较强的非线性时,用一维减维模型求功能函数的前k阶矩时精度不高,则采用二维减维模型代替原功能函数。对随机变量进行逆正态变换,且利用文献[80]给出的公式对功能函数G(X)进行二维减维,则功能函数可以写为:


Zhao等[79]提出了新点估计法来计算功能函数的前k阶矩,其核心思想是通过逆正态变换(Rosenblatt变换)[81]将原始随机变量转换到标准正态空间,再利用标准正态变量的估计点和权重估计函数的前四阶矩。非正态随机变量的估计点可表示为:

式中:Φ(U)为标准正态变量的分布函数;FX(X)为原变量的分布函数;xj为一般随机变量;uj为标准正态变量。
标准正态变量的估计点ui和权重Pi为:
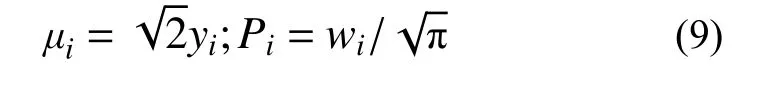
式中,yi和wi是加权函数为exp(−y2)的Hermite积分的横坐标和权重[82],于是可求得七点估计的ui和Pi[79],取值见表7。

表7 标准正态变量的估计点和权重Table 7 Sampling points and weights of standard normal variables
2.2 基于立方正态分布的简化四阶矩法
由可靠度指标定义,可得到基于二阶矩法的可靠度指标βSM和基于四阶矩法的可靠度指标βFM的关系[83]:
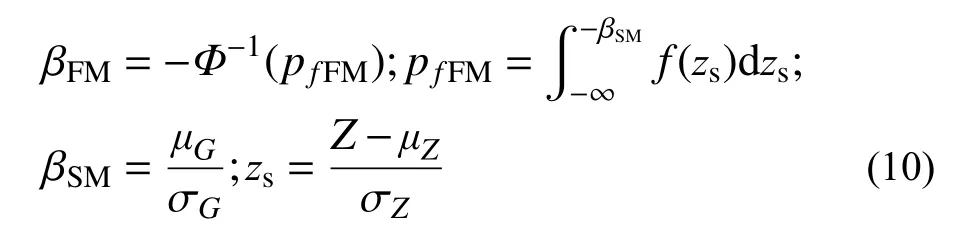
式中,zs为标准化后的随机变量。
Zhao等[84]提出了简化四阶矩计算公式,其基本原理是将随机变量Z标准化后的变量zs近似表示为标准正态变量u的三次多项式:
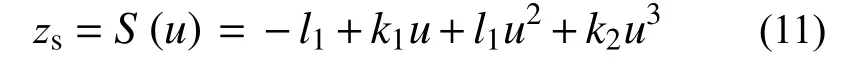
式中,系数l1、k1和k2见详文献[84]。
对式(11)进行z-u转换,可得到:

式中,系数p和系数D见文献[84]。以上关系可以简写为u=S−1(zs)。
由式(10)和式(12)可得,基于四阶矩法和二阶矩法的可靠度指标[85]的关系为:

而传统一次二阶矩法的可靠度指标计算公式为:

2.3 可靠度计算步骤
根据前述2.1的简化四阶矩法,可以求得钢管混凝土轴压承载力公式的可靠度指标β。
1)确定影响可靠度的随机变量为截面尺寸(D,B)、钢管厚度(t)、荷载效应(SGk,SQk)、计算模式不定性(kp)、混凝土强度(fc)、钢管强度(fy),利用MATLAB对基本随机变量进行抽样,获得抗力R统计参数;
2)建立功能函数Z=G(X),对功能函数进行降维处理,利用随机变量R、SGk、SQk的统计参数以及新点估计法计算G(X)的前四阶矩;
3)用简化四阶矩法求得可靠度指标βFM。
3 可靠度结果与分析
3.1 截面形状和含钢率的影响
运用基于一维与二维降维模型的简化四阶矩法计算可靠度指标,设置变化参数为截面形状和含钢率。荷载组合为SG+SL住,取荷载比ρ为1.0,混凝土类别为C40,钢材类别为Q235。
图2为不同截面形状的可靠度指标变化规律,可见由于八边形、六边形、椭圆形和圆端形截面钢管混凝土短柱轴压承载力实验数据少,其δkp较小,故抗力R的δR较小,由式(14)可知,可靠度指标β较大,而圆形和矩形截面的δkp较大,故可靠度指标β较小。由于本文的功能函数为一维函数,采用一维降维模型和二维降维模型得到的结果几乎完全相同,故以下均用一个图表达结果。

图2 截面形状和含钢率变化对钢管混凝土轴压承载力可靠度指标的影响Fig.2 Influence of section shape and steel ratio on reliability index
图3和图4分别为圆形截面和全部截面统计的计算模式不定性系数下,截面形状和含钢率变化对钢管混凝土轴压承载力公式可靠度指标的影响规律,可见:1) 钢管混凝土轴压承载力公式可靠度指标都能满足目标可靠度指标3.2[86]的要求,由于圆形截面统计的δkp较大而全部截面统计的δkp较小,导致全部截面统计计算模式不定性系数下钢管混凝土轴压承载力公式可靠度指标偏大,但可靠度指标差别不超过5%,因此对于不同截面形式,均采用全部截面统计计算模式不定性系数分析其他参数的影响;2) 由于圆形、六边形和八边形截面的钢管形状约束系数k1较大,使得功能函数的方差较大,导致可靠度指标较小;3) 随着含钢率α增大,力比Φs=fyAs/(fcAc)均值增大而钢管对混凝土的约束效率降低,变异系数不变,导致抗力随机变量的变异系数略增大,使得可靠度指标β略减小。此外,对随机变量R、SQk、SGk进行随机取样,代入功能函数Z,其失效区间的占比随着含钢率的增加呈非线性增长,故结构的失效概率随着含钢率的增加而增加。

图3 截面形状和含钢率变化对钢管混凝土轴压承载力可靠度指标的影响Fig.3 Influence of section shape and steel ratio on reliability index

图4 截面形状和含钢率变化对钢管混凝土轴压承载力可靠度指标的影响Fig.4 Influence of section shape and steel ratio on reliability index
3.2 混凝土和钢管强度等级的影响
钢管混凝土的荷载组合为SG+SL住,取荷载比ρ为1.0,含钢率α为0.04,钢材类别为Q235。图5所示为混凝土类别变化对可靠度指标的影响规律,可见随着混凝土等级的增加,随机变量fc的变异系数减小,导致抗力随机变量的变异系数减小,使得可靠度指标β变大。

图5 混凝土类别对钢管混凝土轴压承载力可靠度指标的影响Fig.5 Influence of concrete type on reliability index of axial bearing capacity of concrete filled steel tube
钢管混凝土的荷载组合为SG+SL住,取荷载比ρ为1.0,含钢率α为0.04,混凝土类别为C40。图6所示为钢材类别变化对可靠度指标的影响规律,可见随着钢材等级的增加,随机变量fy的变异系数略微减小,使得可靠度指标β略微增大。

图6 钢材类别对钢管混凝土轴压承载力可靠度指标的影响Fig.6 Influence of steel type on reliability index of axial bearing capacity of concrete filled steel tube
3.3 荷载比和荷载组合的影响
钢管混凝土的荷载组合为SG+SL住,取含钢率α为0.04,混凝土类别为C40,钢材类别为Q235。图7所示为荷载比变化对可靠度指标的影响规律,分析结果表明,当仅有荷载比为变量且ρ约为1.0时,利用条件极值求得SGk+SQk值较小,故失效概率较小,可靠度指标较大,而两者方法的计算结果略有差别:1) 采用MCS法时,当ρ=2.0时,可靠度指标最小,而ρ=0.5~1.0时,可靠度指标较大且极差不超过0.03;2) 采用简化四阶矩法时,当ρ=0.25时,可靠度指标最小,而ρ=0.5~2.0时,可靠度指标的极差约为0.05,当ρL=1.0时,可靠度指标最大。
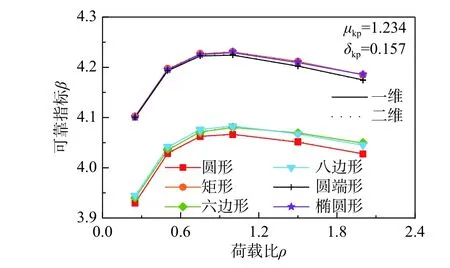
图7 荷载比对钢管混凝土轴压承载力可靠度指标的影响Fig.7 Influence of load ratio on reliability index of axial bearing capacity of concrete filled steel tube
钢管混凝土的荷载比ρ为1.0,含钢率α为0.04,混凝土类别为C40,钢材类别为Q235。图8所示为活载类别变化对可靠度指标的影响规律,可见由于办公室活载的均值系数小于住宅楼面活载的均值系数,而二者的方差相差很小,故荷载组合为恒载和办公室活载时,荷载效应较小,可靠度指标较大。
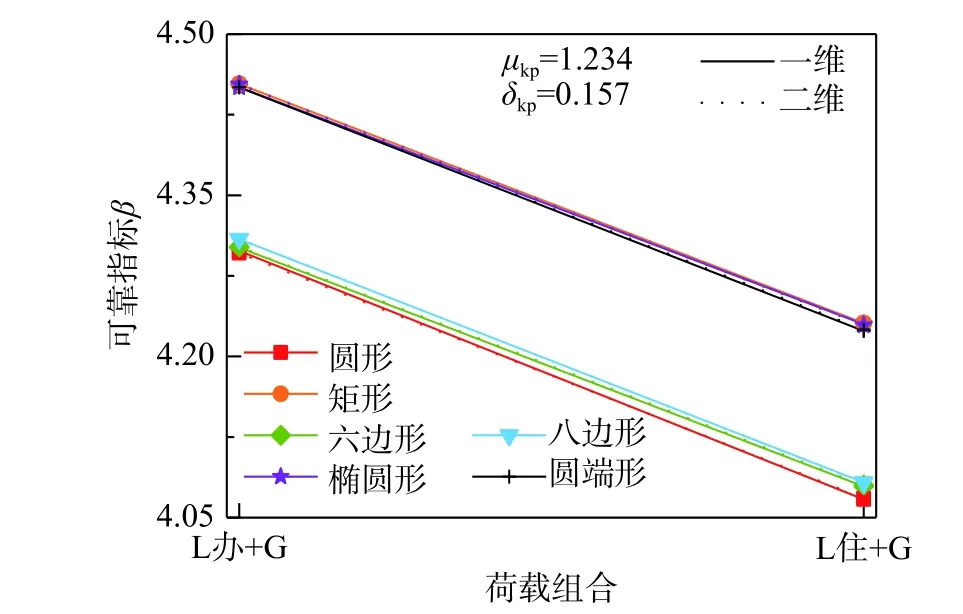
图8 活载类别对钢管混凝土轴压承载力可靠度指标的影响Fig.8 Influence of live load category on reliability index of axial bearing capacity of concrete filled steel tube
4 结论
本文采用简化四阶矩法对钢管混凝土轴压承载力公式进行可靠度分析,结论如下:
(1) 不同截面形状的钢管混凝土轴压承载力公式均高于3.7,满足目标可靠指标3.2[86]的要求。
(2) 对于同一截面形状的钢管混凝土轴压构件,当办公室活载:恒载=1.0时,混凝土强度越高,可靠指标略增大。
