联肢加劲钢板剪力墙滞回性能试验研究与数值分析

马尤苏夫，崔 聪，周清汉，杨 烊，孙博闻

(1. 西安科技大学建筑与土木工程学院，陕西，西安 710054；2. 中机国际工程设计研究院有限责任公司，湖南，长沙 410007)

钢板剪力墙结构由剪力墙板、水平边缘构件(边框梁)和竖向边缘构件(边框柱)组成，是一种高效的抗侧力体系[1 − 3]。应用于高层建筑时，钢板剪力墙的抗剪需求通常容易满足。但我国的相关规范均要求钢板剪力墙主要承受水平剪力，不宜承担竖向荷载[4 − 6]。因此，水平荷载产生的倾覆弯矩使边框柱受到极大的弯矩和轴力作用，导致边框柱截面过大。同时，工程应用中常需要在剪力墙上为门窗、电梯或水电管道等设置洞口。为解决以上问题，可将2片钢板剪力墙通过钢连梁相连，组成联肢钢板剪力墙，如图1所示。水平荷载产生的倾覆弯矩使联肢钢板剪力墙的内、外柱柱脚分别产生弯矩MIVBE、MEVBE和轴力PIVBE、PEVBE(图1(a))。各墙肢内、外柱的轴力可转化为力偶MPIER和墙肢轴力PPIER(图1(b))。与独立作用的单肢钢板剪力墙相比，连梁对墙肢的耦联作用还可使左右墙肢轴力PPIER产生额外的力偶MCOUP抵抗倾覆弯矩(图1(c))。

图1 联肢钢板剪力墙Fig.1 The coupled steel plate shear walls

目前国内外学者已对联肢剪力墙结构进行了一定的研究。田建勃等[7]对采用钢板-混凝土组合连梁的混合联肢剪力墙结构进行了数值模拟，分析了结构的应力分布和塑性铰发展规律，研究了耦联率、连梁截面、墙肢高宽比、总高度和楼板作用等参数对结构抗震性能的影响。刘阳等[8]对5个1/2比例的钢连梁-钢板混凝土组合剪力墙组合件进行了低周反复加载试验。研究表明，连梁跨高比较小的试件具有良好的塑性性能，连梁整体剪切屈服，其抗震性能优于连梁发生弯曲破坏的试件。Li等[9]从6层联肢钢板剪力墙原型结构中选取底部2层半制作了缩尺试验试件，进行了低周反复加载试验和数值分析。研究表明，试件的破坏形态与设计目标相符，可根据结构形成理想屈服机制时的层间位移角确定连梁的转动能力需求。Borello等[10]进行了2个3层联肢钢板剪力墙试件的低周反复加载试验。研究表明，联肢钢板剪力墙具有良好的延性和耗能能力，承载力退化稳定。王萌等[11]对联肢和单肢钢板剪力墙结构进行了数值分析。研究表明，连梁的耦联作用可提高结构的抗震性能，设计时可考虑钢板剪力墙边框抵抗水平荷载的贡献。

截至目前，针对联肢钢板剪力墙的少量研究均采用北美与日本常用的非加劲钢板剪力墙，且周边框架均为H型钢。而我国的工程实践中，多选用加劲钢板剪力墙，且竖向边缘构件常采用钢管混凝土柱，如天津津塔的核心筒结构采用了槽钢竖向加劲钢板剪力墙，竖向边缘构件采用了圆钢管混凝土柱[12]，苏州现代传媒广场采用了井字加劲钢板剪力墙[13]。为研究采用钢管混凝土竖向边缘构件的联肢加劲钢板剪力墙的滞回性能，设计了3个1/3比例的3层联肢钢板剪力墙试件，进行低周反复加载试验，得到了联肢钢板剪力墙试件的荷载-位移滞回曲线和破坏形态，对试件的骨架曲线、应力发展、延性和耗能能力等进行了分析，并利用有限元软件ABAQUS对试件进行了数值模拟。

1 试验概况

1.1 试件设计

设计了3个1/3比例的3层联肢钢板剪力墙试件。参考天津津塔的结构布置，根据实验室加载条件确定剪力墙板的厚度和试件的轮廓尺寸。随后采用文献[14]的方法设计了边框梁、柱的截面。由于各国规范均尚未提出联肢钢板剪力墙中钢连梁的设计方法，文献[15]根据偏心支撑消能梁段的设计方法进行了钢连梁的设计。研究表明，为获得更好的受力性能，消能梁段宜设计为剪切破坏模式[16]。因此，试件的钢连梁截面根据《建筑抗震设计规范》(GB 50011−2010)[17](以下简称《抗规》)中消能梁段发生剪切破坏的条件设计，即净长度a小于1.6Mlp/Vl。其中Mlp、Vl分别为消能梁段的塑性受弯、受剪承载力。

各试件层高、跨度及截面尺寸相同，钢板剪力墙边框柱采用方钢管混凝土柱，边框梁与连梁均采用H形截面钢梁，墙板采用热轧钢板，梁柱节点均采用隔板贯通式全焊接节点，钢板剪力墙与边框梁、柱之间通过鱼尾板连接，鱼尾板与钢板剪力墙、边框梁、柱采用双面角焊缝焊接。试件的剪力墙板分别采用非加劲(试件CSPSW-US)、槽钢竖向加劲(试件CSPSW-CS)和井字加劲(试件CSPSW-GS)的形式。槽钢加劲肋采用双面角焊缝焊与墙板连接。在井字加劲肋相交处焊接与肋板等高的圆管，剪力墙板上相应位置开设直径13.5 mm螺栓孔，通过8.8级M12高强度螺栓和垫板将井字加劲肋安装在剪力墙板两侧。试件几何尺寸见图2，构件截面见表1。

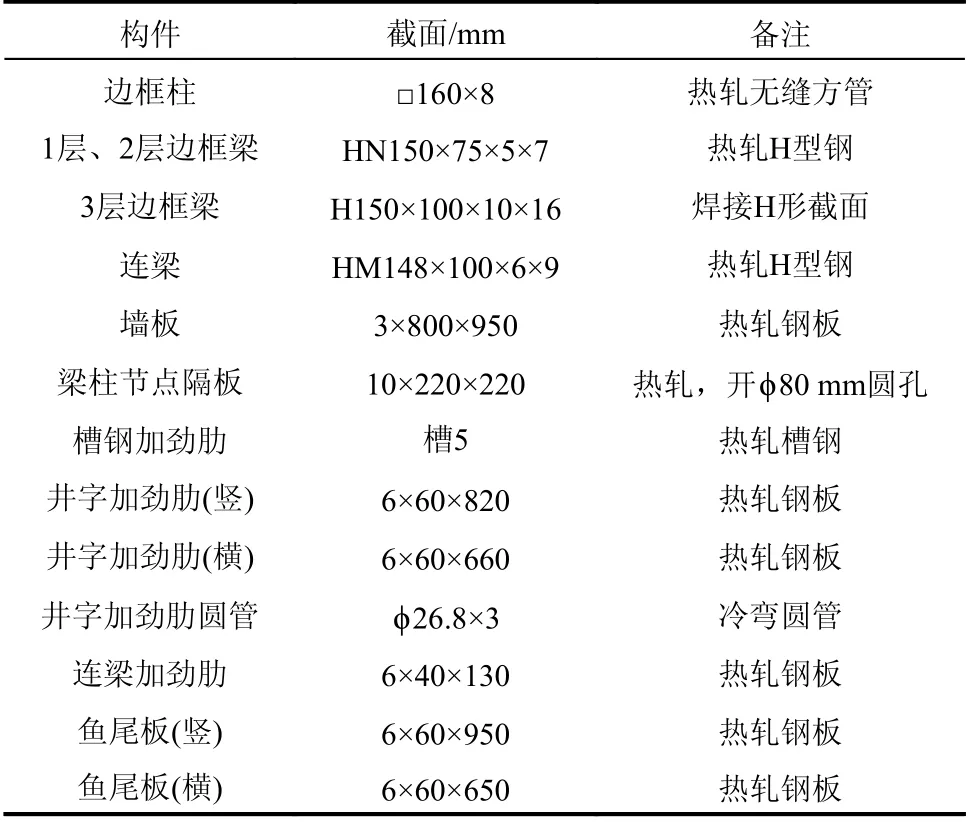
表1 构件与板件截面Table 1 Sections of members and plates

图2 试件几何尺寸Fig.2 Dimensions of specimens

1.2 材料性能

试件的钢材均为Q235B级钢，拉伸试验测得材料的屈服强度、抗拉强度、弹性模量和伸长率见表2。方钢管内填C30微膨胀细石混凝土，浇筑混凝土的同时制作了边长为150 mm的立方体试块，测得平均立方体抗压强度为43 N/mm2。

表2 钢材力学性能Table 2 Mechanical properties of steels

1.3 试验装置及加载方案

加载装置如图3所示。竖向荷载通过门架梁下的千斤顶施加，荷载分配梁(图3(b))将竖向荷载传递至柱顶，各柱受到350 kN的竖向荷载，轴压比0.25。千斤顶上部设置可随柱顶水平移动的滚动装置。试件南北两侧各放置1个量程1000 kN的水平作动器，一端与反力墙相连，另一端与试件顶部的“中”字形水平荷载分配梁相连。水平荷载分配梁东、西两端与试件顶梁上的悬臂加载端头固定，将水平荷载分别传递至两肢墙体顶部。试件弹性阶段加载由荷载控制，每级增量200 kN，循环1周。试件屈服后水平荷载由位移控制，以屈服位移Δy的0.5倍为增量，每级循环3周。水平反复加载先推(东)后拉(西)。加载程序如图4所示。

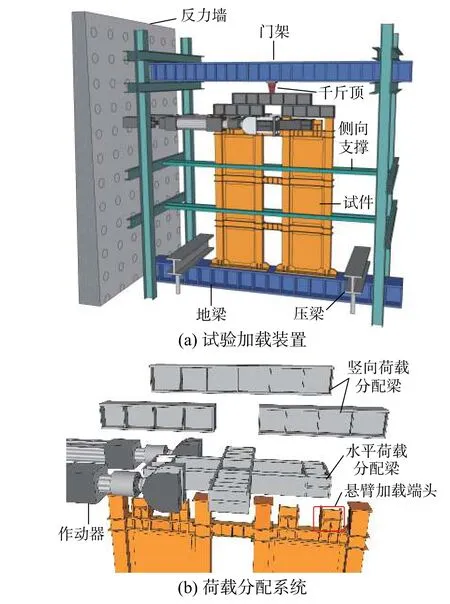
图3 加载装置Fig.3 Test setup

图4 加载程序Fig.4 Loading protocol

1.4 测点布置

各试件测点布置方案相同，如图5所示。在试件各层东、西两端布置位移计，测量试件各层水平位移。在地梁两端布置位移计，监测地梁的滑移。在墙板角部、梁端、梁柱节点及柱脚等位置布置应变片。

图5 测点位置Fig.5 Arrangment of instruments

2 试验现象

试件的加载过程可分为弹性阶段、弹塑性阶段和破坏阶段。加载初期，水平荷载主要由墙板承担。试件CSPSW-US、CSPSW-CS的墙板分别于水平荷载200 kN、600 kN时屈曲。试件CSPSWUS的墙板整体屈曲。受加劲肋约束，试件CSPSWCS的加劲肋两侧墙板发生局部屈曲。屈曲后墙板形成多道斜向屈曲半波。反向加载时，墙板屈曲恢复并沿另一对角线反向屈曲，导致试件发出巨大声响。井字加劲肋具有良好的加劲效果，较大地提高了墙板的临界屈曲应力，试件CSPSW-GS的墙板在荷载控制的加载阶段未发生屈曲。水平荷载600 kN时，试件CSPSW-US的最大层间位移角超过1/250，800 kN时试件CSPSW-CS、CSPSWGS的最大层间位移角超过1/250。

根据试验过程中荷载-位移曲线的斜率变化，各试件的屈服位移Δy均取为20 mm。进入位移控制加载阶段后，墙板发生了明显的塑性变形，形成了无法恢复的屈曲折痕。墙板角部横、竖向鱼尾板间的空隙导致此处应力集中，各试件的墙板四角相继撕裂，如图6(a)所示。试件CSPSW-GS墙板角部撕裂最早出现(水平位移1.0Δy)，随后墙板在井字加劲肋划分的区格内局部屈曲。试件CSPSW-US、CSPSW-CS墙板分别于水平位移2.0Δy、1.5Δy时角部撕裂。方钢管混凝土柱良好的强度和刚度使墙板抗侧性能得到了充分发展，墙板屈曲和角部撕裂后水平荷载仍继续增长。水平位移超过2.5Δy后，各试件各层连梁与柱子的节点焊缝自下而上相继断裂，如图6(b)所示。

加载位移3.0Δy时，各试件的最大层间位移角均超过了1/50。各试件整体水平位移3.0Δy～3.5Δy时，塑性变形的积累使墙板中部陆续撕裂(图6(c)、图6(d))，部分墙板退出工作，各试件的水平荷载达到峰值。随后钢板剪力墙1层、2层边框梁端部相继屈曲(图6(e))，各试件的承载力逐渐退化。由于受到单侧拉力场的作用，3层边框梁在设计时采用了较大的截面，同时水平加载传力系统加强了顶梁截面，试验中顶梁未发生破坏。试件CSPSWUS、CSPSW-CS和CSPSW-GS的方钢管混凝土柱脚分别于位移4.5Δy、4.5Δy和4.0Δy时发生鼓曲，形成塑性铰，如图6(f)所示。随着各构件的塑性破坏逐渐加剧，水平荷载降至峰值荷载的85%，试验结束。试件CSPSW-US、CSPSW-CS和CSPSWGS的极限位移分别5.5Δy、5.0Δy和5.0Δy。各试件的破坏顺序如图7所示。各破坏状态对应的最小层间位移角见表3。

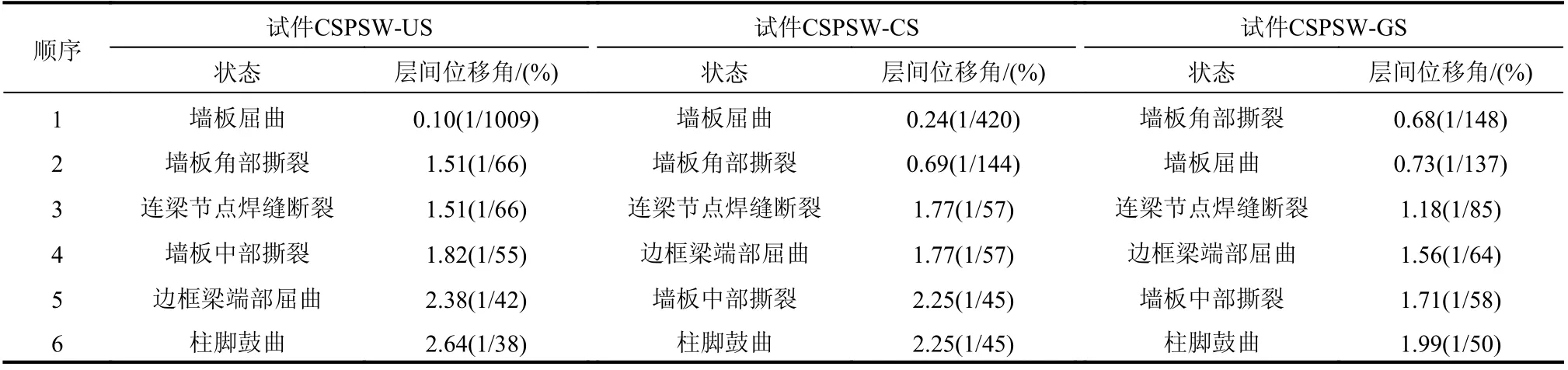
表3 破坏状态对应层间位移角Table 3 Story drift at each damage state

图6 试件局部破坏Fig.6 Local damage of specimens

图7 试件破坏顺序Fig.7 Failure sequence of specimens

3 试验结果与分析

3.1 滞回曲线

图8为各试件的荷载-位移滞回曲线。屈服荷载时各试件的滞回环如图9(a)所示，各试件滞回环的包络面积均较小，且基本重合，表明弹性阶段各试件的性能较接近。进入弹塑性阶段，墙板屈曲形成的拉力场为试件提供了较高的刚度和承载力。卸载后的反向加载过程中，墙板屈曲恢复，拉力场消失。此时部分墙板暂时退出工作，水平荷载主要由钢板剪力墙边框和钢连梁承担，试件刚度下降，滞回曲线出现捏缩效应。随着反向加载位移的增加，墙板再次屈曲，形成反向拉力带，滞回曲线斜率再次增大。图9(b)为峰值荷载时各试件滞回环的对比。试件CSPSW-US与CSPSW-CS的滞回环均呈反“S”形，其中试件CSPSW-US滞回环的捏缩效应最严重。井字加劲肋对墙板有较强的屈曲约束作用，因此试件CSPSWGS的滞回环较饱满。图9(c)为极限荷载时各试件滞回环的对比。试件CSPSW-US与CSPSW-CS的滞回环基本重合，表明进入破坏阶段后竖向槽钢加劲肋对墙板的约束减弱，两个试件的墙板破坏程度相近。采用井字加劲肋的试件CSPSW-GS墙板破坏较轻，滞回环面积较大，捏缩效应较弱。

图8 滞回曲线Fig.8 Hysteresis curves

图9 典型滞回环对比Fig.9 Comparison of typical hysteresis loops

3.2 骨架曲线

图10为各试件的荷载-位移骨架曲线。由于加劲肋仅提高了墙板的屈曲应力，未直接参与抵抗水平荷载，墙板屈曲前各试件的刚度较接近，骨架曲线基本重合。墙板屈曲后垂直于拉力场方向存在主压应力，如图11所示。该应力通常大于墙板的弹性剪切屈曲临界应力τcr，当墙板的τcr较大时，主压应力对墙板承载力的贡献不可忽略[18]。

图10 骨架曲线Fig.10 Envelope curves

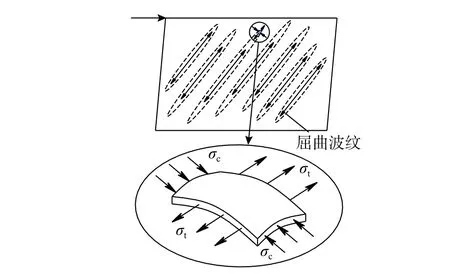
图11 墙板屈曲后应力状态Fig.11 Stress state of the plate

根据《钢结构设计标准》(GB 50017−2017)[4]附录F求得试件CSPSW-US、CSPSW-CS和CSPSWGS的τcr分别为26.3 MPa、78.9 MPa和883.1 MPa。试件CSPSW-GS的τcr超过了材料抗剪强度，表明墙板先屈服后屈曲。因此，试件CSPSW-GS承载力最高，其次是试件CSPSW-CS，试件CSPSW-US承载力最低。

试件骨架曲线特征点见表4。采用通用屈服弯矩法判定试件屈服，相应荷载为屈服荷载，水平荷载降至峰值荷载85%时对应的荷载和位移为极限荷载和极限位移。试件CSPSW-GS和CSPSWCS的峰值荷载平均值分别比试件CSPSW-US提高了11.7%和6.9%。各试件极限状态的层间位移角均大于《抗规》[17]中1/50的弹塑性层间位移角限值。延性系数µ为极限位移与屈服位移之比，试件CSPSW-US、CSPSW-CS和CSPSW-GS的延性系数平均值分别为5.2、5.5和4.5，表明不同加劲形式的联肢钢板剪力墙均具有良好的延性。

表4 整体骨架曲线特征点Table 4 Characteristic points on global envelope curves

3.3 应力分析

根据试验采集的应变数据，可计算梁、柱腹板和墙板的von Mises应力，梁、柱翼缘的正应力。选取各构件中最先屈服的测点，得到构件的应力发展，如图12所示。图中纵轴以应力比σ/fy的形式表示，σ为根据应变花数据计算的von Mises应力或根据应变片数据计算的截面正应力，fy为材料实测屈服强度。

图12 构件应力发展Fig.12 Stress development of components

各试件的墙板均首先屈服。由于墙板的应变测点位于屈曲后应力较大的对角线处，而井字加劲肋对墙板屈曲有显著的约束作用，使墙板应力分布更均匀。因此，试件CSPSW-US和CSPSW-CS的墙板屈服较早，屈服时层间位移角均小于0.3%，试件CSPSW-GS墙板屈服时层间位移角大于0.3%。墙板屈服后连梁与边框梁先后屈服。方钢管混凝土柱同时受轴力和弯矩作用，应力增长较快，柱脚屈服较早。但柱脚屈服时各试件第1层的层间位移角均大于0.45%(1/222)，已超过《抗规》[17]中1/250的弹性层间位移角限值。同时，根据应变数据判定材料屈服，仅代表构件截面的边缘纤维发生了屈服，此时，方钢管混凝土柱仍具有良好的弹塑性变形能力。根据试验现象，柱脚的破坏晚于其他构件，柱脚形成塑性铰时，各试件层间位移角均已超过1/50。除柱脚外，各试件方钢管混凝土柱其他测点处均未发生屈服。

3.4 耗能能力

试件的耗能能力以荷载-位移滞回曲线所包围的面积来衡量，用等效黏滞阻尼系数ζeq评价，按式(1)计算，各部分面积如图13所示。各试件等效黏滞阻尼系数ζeq见图14。

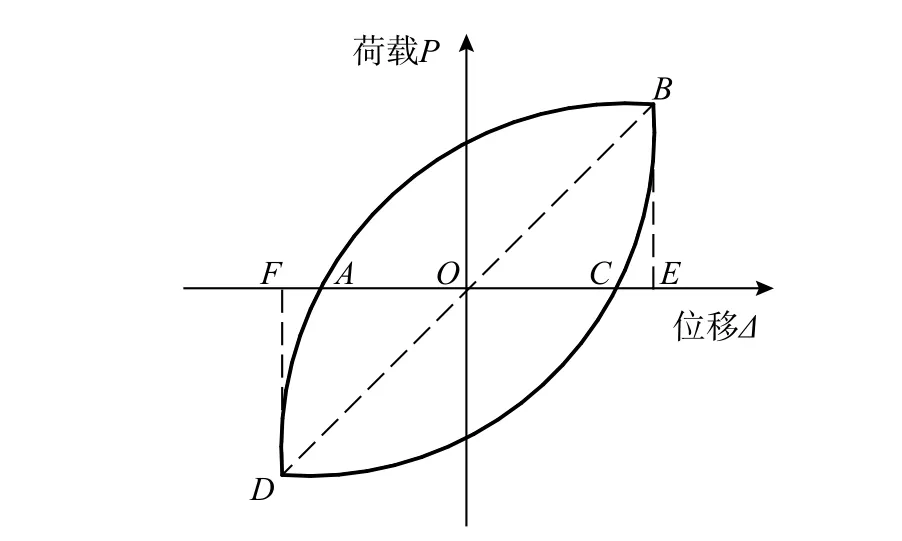
图13 等效黏滞阻尼系数计算Fig.13 Equivalent viscous damping coefficient cauculation

图14 等效黏滞阻尼系数Fig.14 Equivalent viscous damping coefficient

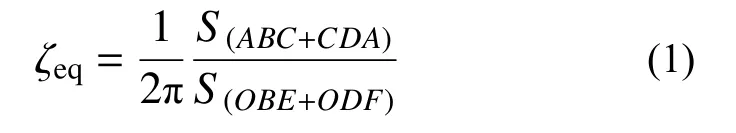
式中：S(ABC+CDA)为图13中滞回曲线所包围的面积；S(OBE+ODF)为图13中三角形OBE与ODF包围的面积之和，代表结构的弹性应变能。

各试件第2层层间耗散的能量均大于其他两层，约占试件总耗能的40%。试件CSPSW-US的墙板缺少加劲肋约束，滞回曲线捏缩效应最严重，耗能能力最弱。峰值荷载时，试件CSPSWGS和CSPSW-CS的ζeq分别比试件CSPSW-US的ζeq提高了65.9%和19.9%。表明设置加劲肋可提高联肢钢板剪力墙结构的耗能能力。

4 数值分析

4.1 有限元模型建立

采用有限元分析软件ABAQUS对试件进行精细化数值模拟。各模型的几何尺寸与试件完全相同。混凝土在钢管的被动约束下，处于三轴受压状态，文献[19]通过大量的试验研究和理论分析，提出了一种考虑钢管约束效应的混凝土单轴应力-应变模型。混凝土的单轴受压应力-应变曲线如图15所示，模型的数学表达式如式(2)所示。混凝土受拉软化性能采用基于脆性破坏概念的能量破坏准则，该准则定义开裂的单位面积作为材料参数，采用应力-断裂能关系描述混凝土的脆性性能，假定混凝土开裂后应力线性减小，相关计算公式见文献[19]。

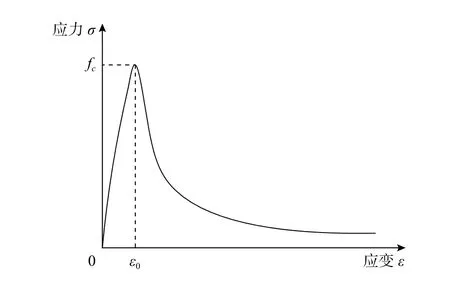
图15 混凝土单轴受压应力-应变曲线Fig.15 Uniaxial compression stress-strain curve of concrete

当混凝土单轴受力处于应力-应变曲线的软化段时，混凝土的卸载响应会因材料的损伤而发生削弱，其卸载刚度会随之降低。采用塑性损伤模型模拟混凝土卸载时刚度的降低，该模型综合了非关联多轴硬化塑性和各向同性线性损伤模型，可以用来模拟循环往复荷载作用下，混凝土开裂和压碎引起的不可恢复的损伤。混凝土材料的损伤因子计算公式见文献[19]。

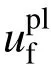
模型中混凝土采用8节点线性减缩积分实体单元(C3D8R)，钢材采用考虑大变形的线性减缩薄壳单元(S4R)。模型的边界条件与试验一致，约束试件底部平动和转动自由度。在二层和三层层间，设置柱子的平面外约束。四个柱顶上方施加竖向荷载。在顶梁上翼缘中部施加水平位移。模型中面与面之间的接触法向为“硬”接触，“硬”接触可以传递接触面间的压力和变形。切向采用库仑摩擦模型，通过定义摩擦系数模拟钢与混凝土之间的黏结与滑移，钢管与混凝土间的摩擦系数取为0.6[19]。模型CSPSW-GS中，井字加劲肋侧边与墙板间的摩擦系数取为0.3，井字加劲肋横纵向相交处的节点与墙板对应位置通过绑定约束模拟螺栓对加劲肋的固定作用。对模型进行屈曲分析，采用多阶屈曲模态的叠加模拟墙板的初始几何缺陷。有限元模型施加的初始缺陷与试验测量结果一致，取为2 mm。有限元模型的网格划分与边界条件如图16所示。

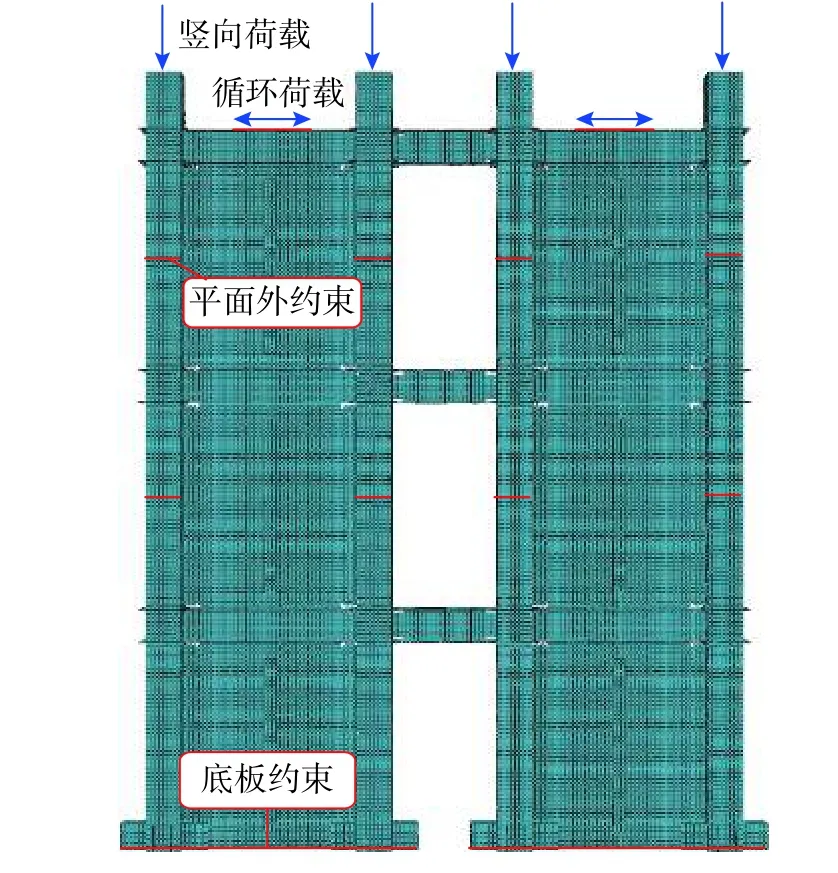
图16 模型CSPSW-CSFig.16 The model of CSPSW-CS

4.2 滞回曲线和骨架曲线对比

有限元模型与试验试件的滞回曲线和骨架曲线的对比如图17所示。受材料的离散性、试件加工导致的初始缺陷以及加载装置等因素的影响，与试验相比，有限元模型的滞回曲线均更饱满。弹性阶段，有限元曲线刚度略大于试验曲线，有限元模型的峰值荷载略高于试验。加载后期，有限元模型强度和刚度的退化程度较小，曲线高于与试验曲线。整体而言，有限元模型与试验吻合较好，可包络试验曲线。表5为有限元模型与试验试件初始刚度和峰值承载力的对比，模拟值与试验值的误差小于6.5%，表明所建立的有限元模型可较好地反映试验试件的滞回性能。

图17 结果对比Fig.17 Comparison of results

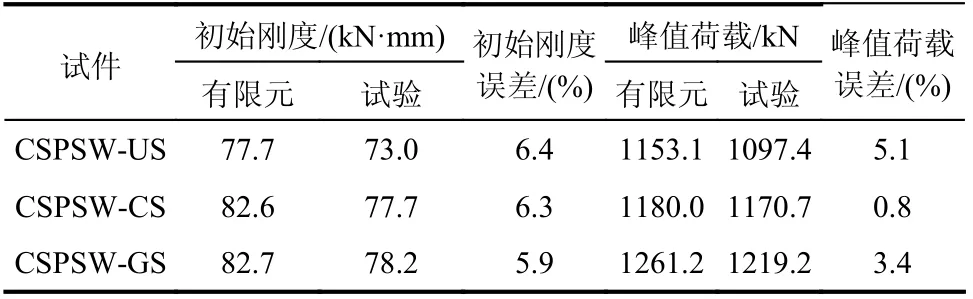
表5 有限元与试验结果对比Table 5 Comparison between analyses and tests

4.3 破坏形态对比

模型CSPSW-US与CSPSW-CS达到屈服荷载前，墙板发生平面外屈曲。屈服荷载时，有限元模型部分墙板的主拉应力达到屈服强度，且角部存在明显的应力集中，连梁和边框梁节点处腹板也基本屈服。模型整体位移角0.9%(1/110)时，柱脚钢管屈服。峰值荷载时，墙板、连梁、边框梁和柱脚的屈服范围增大，材料开始出现损伤(D>0)。模型整体位移角2.4%(1/41)时，墙板中部撕裂(D=1)。随后连梁和边框梁的腹板撕裂，柱脚钢管出现损伤。加载结束时，模型整体位移角3.3%(1/30)，柱脚区域钢管的损伤因子D均小于0.26，如图18所示。表明加载过程中柱脚未发生严重破坏。有限元模型和试验试件的最终破坏形态对比如图19所示。数值分析中，材料断裂后相应单元即被删除。墙板屈曲、墙板角部和中部的撕裂、连梁和边框梁节点处腹板断裂、柱脚鼓曲等破坏形态均与试验相符，表明有限元模型可充分地反映试件的塑性变形发展情况。

图18 柱脚钢管损伤Fig.18 Damage at column base

图19 破坏形态对比Fig.19 Comparison of failure modes

4.4 内力分析

通过ABAQUS的自由体切片(free body cut)可提取模型各构件的内力，图20为模型CSPSWCS一层各构件的内力发展情况，其他模型与其规律相似。由于各构件受力特点不同，图中纵坐标采用构件内力与其理论承载力之比。构件理论承载力根据我国相关规范计算[4−5,21]，其中墙板采用抗剪承载力，连梁和边框梁均先发生剪切屈服，故采用腹板抗剪承载力，柱子采用压弯或拉弯承载力。加载过程中墙板剪力最先达到理论承载力，随后连梁、边框梁和柱子的内力达到理论承载力。墙板内力退化较早，随后连梁和边框梁的内力发生退化。加载过程中，方钢管混凝土柱的承载力稳定，未发生明显退化。极限状态时，方钢管混凝土柱的内力与理论承载力之比大于1.2。

图20 模型CSPSW-CS内力发展Fig.20 Internal force of model CSPSW-CS

对比表明，各模型中连梁、边框梁和柱子的内力发展规律相似。受加劲肋影响，各模型的墙板剪力发展存在差异，如图21所示。采用非加劲墙板的模型CSPSW-US，反向加载时未能达到规范规定的承载力。槽钢加劲肋与墙板焊接连接，可参与墙板抗剪，而井字加劲肋未直接与墙板连接，仅对墙板有屈曲约束作用。因此，模型CSPSWCS的墙板承载力略高于模型CSPSW-GS的墙板承载力，二者分别比模型CSPSW-US的墙板承载力提高了29%和21%。

图21 一层墙板内力发展Fig.21 Internal force of web plates at first story

4.5 参数分析

为研究影响联肢钢板剪力墙性能的因素，建立联肢钢板剪力墙有限元模型进行参数分析。以上研究表明墙板井字加劲的联肢钢板剪力墙具有更好的承载力和耗能能力，故选用墙板井字加劲联肢钢板剪力墙，采用工程常用尺寸，利用上述模拟方法建立3层三跨足尺有限元模型。参数分析模型的内嵌钢板屈服强度235 N/mm2，钢管与钢梁屈服强度355 N/mm2，钢材弹性模量均为2.06×105N/mm2。方钢管内填混凝土轴心抗压强度26.8 N/mm2，弹性模量3.25×104N/mm2。基准模型的截面尺寸如表6所示，几何尺寸见图22。

图22 模型几何尺寸Fig.22 Dimensions of numerical model

表6 模型构件与板件截面Table 6 Sections of members and plates of model

4.5.1 连梁净跨度影响

参考《建筑抗震设计规范》(GB 50011−2010)中对偏心支撑的规定[17]，连梁净跨度ln与连梁破环模式的关系如表7所示。发生剪切破坏时，钢连梁中部产生剪切塑性铰，发生弯曲破坏时，钢连梁两端产生弯曲塑性铰。钢板剪力墙肢的破坏均为剪力墙板形成斜向拉力带屈服，随后边框梁端与底层柱脚形成塑性铰。建立了不同连梁破坏模式的联肢钢板剪力墙进行滞回分析，研究连梁不同破坏模式下，联肢钢板剪力墙的受力性能。连梁净跨度ln分别为1380 mm(剪切破环)、1580 mm(弯剪破环)和2680 mm(剪切破环)，所有模型其他参数不变。为反映耦联作用对结构性能的提高程度，建立了与模型一侧墙肢尺寸完全相同的单肢钢板剪力墙模型进行对比，承载力和能量耗散的对比结果如图23和图24所示。图中纵轴以承载力比Fu/Fu,s和耗能比Eu/Eu,s的形式表示。Fu和Eu为联肢钢板剪力墙模型的水平承载力和耗能，Fu,s和Eu,s为相应单肢钢板剪力墙模型水平承载力和耗能的2倍。随着连梁净跨度的增加，左、右墙肢轴力PPIER(图1)间的力臂增大，从而墙肢间的力偶MCOUP增大。图23和图24体现了联肢钢板剪力墙相较于采用两片单肢钢板剪力墙承载力和耗能的提高程度。当连梁净跨度增大时，耦联作用对联肢钢板剪力墙承载力的提高程度增大，对耗能的提高程度减小。

图23 连梁净跨度对承载力的影响Fig.23 Influence of net span of coupling beam on bearing capacity

图24 连梁净跨度对耗能的影响Fig.24 Influence of net span of coupling beam on energy dissipation

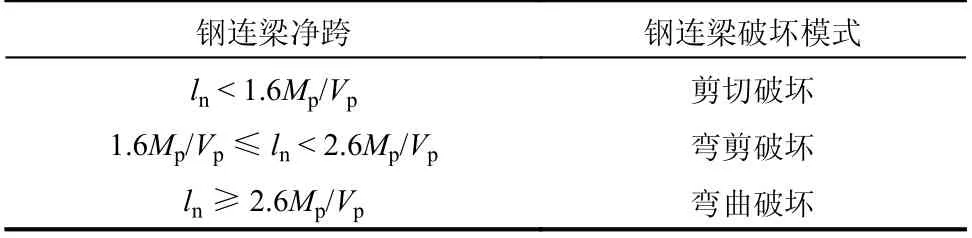
表7 连梁破坏模式Table 7 Failure modes of coupling beams

图25为加载过程中各模型一层构件内力的变化情况，纵坐标为构件内力与其理论承载力之比，计算方法与4.4节相同。墙板和连梁是联肢钢板剪力墙体系中的主要抗侧力构件，边框梁和边框柱的破坏均晚于前两者，故图中仅体现了墙板和连梁的内力发展情况。内力分析结果表明，ln=1380 mm和1580 mm模型的连梁首先发生剪切破坏，ln=2680 mm模型的连梁发生弯曲破坏。不同连梁净跨度模型的墙板内力发展趋势未发生明显变化。而净跨度较小的连梁线刚度较大，因此受力较大，更早达到其理论承载力。

图25 连梁净跨度对构件内力的影响Fig.25 Influence of net span of coupling beam on internal force of members

4.5.2 墙板净跨度影响

增加墙板净跨度可提高钢板剪力墙的抗剪面积，从而提高抗剪承载力。为研究墙板净跨度对联肢钢板剪力墙性能的影响，建立了墙板净跨度lw分别为2400 mm、2800 mm和3200 mm的模型。各模型承载力和耗能对比见图26和图27。与两片单肢钢板剪力墙相比，耦联作用对联肢钢板剪力墙承载力和耗能的提高程度随着墙板净跨度的增加而降低。

图26 墙板净跨度对承载力的影响Fig.26 Influence of net span of web plate on bearing capacity

图27 墙板净跨度对耗能的影响Fig.27 Influence of net span of web plate on energy dissipation

各模型一层构件内力变化情况见图28。由于连梁尺寸未发生改变，不同墙板净跨度模型的连梁内力发展趋势未发生明显变化。随着墙板净跨度的增加，墙板的剪切刚度增大，导致墙板受力增大，更早达到其理论抗剪承载力。但墙板净跨度的变化未改变联肢钢板剪力墙的破坏顺序，各模型连梁的剪切破环均先于墙板的破环。

图28 墙板净跨度对构件内力的影响Fig.28 Influence of net span of web plate on internal force of members

4.5.3 连梁抗剪承载力影响

从图1的联肢钢板剪力墙耦联机理可以看出，左、右墙肢轴力PPIER依靠各层连梁剪力传递，产生力偶MCOUP。因此墙肢间力偶的大小受连梁抗剪承载力的影响。建立了连梁腹板厚度tw,CB分别为10 mm、12 mm和14 mm的模型。各模型承载力和耗能对比见图29和图30。与两片单肢钢板剪力墙相比，耦联作用对联肢钢板剪力墙承载力和耗能的提高程度随着连梁腹板厚度的增加而增加。

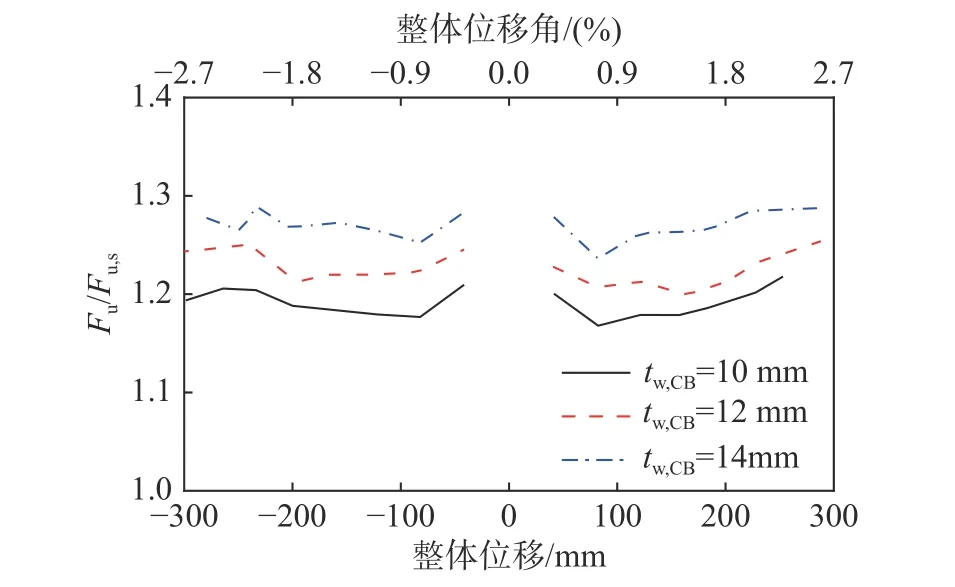
图29 连梁腹板厚度对承载力的影响Fig.29 Influence of web thickness of coupling beam on bearing capacity

图30 连梁腹板厚度对耗能的影响Fig.30 Influence of web thickness of coupling beam on energy dissipation

各模型一层构件内力变化情况见图31。由于墙板尺寸未发生改变，不同连梁腹板厚度模型的墙板内力发展趋势基本未发生变化。腹板厚度较大的连梁更早达到其理论抗剪承载力。但连梁腹板厚度的变化未改变联肢钢板剪力墙的破坏顺序，各模型连梁的剪切破环均先于墙板的破环。

图31 连梁腹板厚度对构件内力的影响Fig.31 Influence of web thickness of coupling beam on internal force of members

5 结论

本文通过低周反复加载试验和数值分析，研究了墙板采用不同加劲方式的联肢钢板剪力墙试件的滞回性能，并对影响联肢钢板剪力墙性能的因素进行了参数分析，得到以下结论：

(1)非加劲和槽钢竖向加劲剪力墙板先屈曲后屈服，井字加劲剪力墙板先屈服后屈曲。进入弹塑性阶段，墙板角部首先撕裂，随后连梁与柱子的节点焊缝断裂，钢板剪力墙边框梁端形成塑性铰，最终试件因柱脚形成塑性铰而破坏。

(2)墙板未加劲试件CSPSW-US滞回环捏缩效应最严重，其次是墙板槽钢竖向加劲试件CSPSWCS。井字加劲试件CSPSW-GS的滞回环较饱满，设置加劲肋可提高结构的耗能能力。试件CSPSWGS和CSPSW-CS的等效黏滞阻尼系数分别比试件CSPSW-US的等效黏滞阻尼系数提高了65.9%和19.9%。

(3)试件CSPSW-GS和CSPSW-CS的承载力分别比试件CSPSW-US的承载力提高了11.7%和6.9%。各试件的延性系数均大于4.5，表明不同加劲形式的联肢钢板剪力墙均具有良好的延性。

(4)数值分析与试验结果吻合较好，初始刚度和峰值承载力误差小于6.5%。加劲肋对连梁、边框梁和柱子的内力影响较小，但可显著提高墙板的抗剪承载力。

(5)相较于两片单肢钢板剪力墙，联肢钢板剪力墙的承载力和耗能随连梁净跨度、墙板净跨度和连梁腹板厚度的变化呈现不同程度的提高，承载力提高20%～40%，耗能提高20%～45%。参数分析中，联肢钢板剪力墙的破坏顺序未受到各因素变化影响。