基于小波时频图与轻量级卷积神经网络的螺栓连接损伤识别

2021-09-23卓德兵

工程力学 2021年9期

卓德兵，曹晖

(1. 重庆大学土木工程学院，重庆 400045；2. 重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045；3. 吉首大学土木工程与建筑学院，张家界 427000)

螺栓连接广泛应用于工程结构，尤其是钢结构和组合结构。在服役期内，结构遭遇的不可避免的振动和冲击等外部作用会导致螺栓连接状态的改变，出现松动、滑移甚至脱落等问题，从而降低结构的刚度、破坏结构的完整性，危及结构安全[1]。因此，螺栓连接状态的监测，对于保证结构安全、避免重大安全事故和降低事故危害性具有重要意义。

目前，常用的螺栓连接损伤检测方法分为基于模态和基于阻抗两类[2]。螺栓松动会改变结构连接状态，从而导致结构模态参数发生相应的变化[3]。将实测的结构模态参数与基准参数比较，从而判断螺栓连接状态是基于模态的检测方法的基本原理。然而，结构的低阶振动参数和低频段传递特性等特征参量对螺栓连接损伤这样的局部特性变化不够敏感[4]。如果要提高特征参量的灵敏度，就需要在高频段甚至极高频段准确测量和识别结构的模态参数，这在目前还存在很大困难。此外，结构模态参数的识别多是基于线弹性振动的假设，会不可避免地过滤掉重要的非线性振动现象。这使得其在螺栓连接状态监测上存在先天不足[5 − 6]。

基于阻抗的方法是比较结构监测状态与基准状态下的高频段阻抗谱，判别螺栓连接的损伤程度。自Sun等[7]首次提出应用压电阻抗方法监测桁架结构的节点状态以来，不少学者研究了基于该方法的螺栓连接状态的监测和辨识[8 − 10]。这种方法受到测点数量的制约。以具有大量的连接节点和螺栓的钢桁架为例，同时监测所有的节点，需要大量的传感器，经济性不佳[2]。而且与基于模态的方法一样，基于阻抗的技术往往对激励和实测环境有严格的要求，比如通常需要结构的某些功能暂时中断，这给在线监测造成了困难[1 − 2]。此外，这类方法使用的采集设备通常较大或昂贵(或二者兼具)，不利于实际应用[7 − 9]。

近年来，利用声音信号进行损伤检测的技术愈发兴起。声音信号具有时间分辨率高，传播具有全向性且不受能见度限制等优点[11]。不同于传统的振动信号测量，需要将传感器固定于被测物体表面且对布点有较高的要求，声音测量属于非接触式测量，采用的传声器测量装置受空间限制少、安装方便且造价相对较低[12]，并能够有效避免加速度传感器测量时普遍存在的饱和及失效现象。Garcia-Perez等[13]基于高分辨率光谱分析的多信号分类算法，利用声音信号对存在单个故障的感应电动机的故障状态进行识别。Amarnath等[14]采用决策树机器学习方法，对从轴承现场附近采集的声音信号进行分析处理，实现旋转机械轴承故障诊断。Madhusudana等[15]提出了一种基于决策树和声信号小波变换技术的故障诊断方法，可以对铣刀表面粗糙度、尺寸公差和刀具状态进行识别和监控。Lu等[16]提出了一种基于瞬态声信号分析的变速器轴承故障诊断方法，该方法可以准确地估计故障引起的脉冲的相位信息，为实现变速电机轴承故障诊断提供了一种简单有效的方法。瞿金秀等[17]构建了一种基于声音信号的结构损伤识别模型，并将该模型应用于实验悬臂梁和铁路转辙机动作杆的裂纹损伤识别。

基于声音信号的损伤识别方法研究目前大多集中在旋转机械领域，借鉴传统的语音识别技术，即通过人为选取特征参数，采用决策树、支持向量机等方法进行建模，识别损伤状态下的声音信号。依靠人工选取的特征往往比较单一并带有较强的主观性。决策树和支持向量机属于浅层模型，需要进行复杂的调参，且每个方法都是针对具体应用，泛化能力及鲁棒性较差，影响了其实用性[18]。近年来，得益于计算机硬件水平的提升，尤其是云计算和大规模GPU并行计算的发展，以深度卷积神经网络为代表的深度学习技术在图像分类、目标检测和图像分割等计算机视觉任务中表现出了巨大的优越性[19]，更多更深的卷积神经网络如AlexNet(2012年)、VGGNet(2014年)、GoogleNet(2014年)、ResNet(2015年)等相继被提出[20 − 22]。深度学习技术主要依靠数据驱动进行特征提取，通过学习大量样本得到深层的、特定的特征表示，对样本集的表征更高效和准确，鲁棒性更强，泛化能力更好。目前，利用深度卷积神经网络解决工程问题成为了众多领域的研究热点[23 − 27]。深度卷积神经网络在声学建模方面也取得了飞速的发展，并逐渐成为语音识别的主流模型[28]。在非语音信号识别中，如环境声音识别[29]，变压器声纹识别[30]，深度学习也有一定的应用。

本文以振动环境下螺栓连接结构为研究对象，提出基于声音信号的螺栓连接损伤智能识别方法。对于常年处于振动环境中的钢桁架结构，如载人索道支架，当结构杆件的连接螺栓发生松动时，螺栓连接界面在钢丝绳和吊篮激励作用下发生碰撞而发出特有的声音信号。与普通旋转机械故障产生的声音信号不同，螺栓松动发出的声音信号具有典型的时变非线性特征，同时考虑到工程结构所处室外环境噪声干扰严重，本文将小波时频图与轻量级卷积神经网络MobileNetv2相结合，充分发挥小波时频分析处理非平稳信号的优势和MobileNetv2强大的图像分类能力，实现基于声音信号的螺栓连接损伤识别。

1 螺栓松动损伤识别原理

1.1 声音信号的预处理

首先，对麦克风采集的声音信号进行分帧、加窗处理，同时求取各帧信号的短时能量。

假设x(n)为麦克风接收到的声音信号离散序列，ω(n) 为窗函数，L为帧长，inc为帧移，N为分帧后的总帧数，则第i帧信号xi(n)可以表示为：

第i帧信号xi(n) 的短时能量E(i)定义如下：

1.2 小波时频分析

经分帧加窗处理之后，对声音信号进行连续小波变换。连续小波变换的公式如下：

式中，母小波ψ 采用Complex Morlet小波。Complex Morlet是一种常用的复值小波，与其它小波相比，该小波在时频两域均具有良好的分辨率，在时频图上反映的时频聚集性好，适合于处理非平稳的声音信号。

将声音信号进行连续小波变换生成为时频图，需要用到matlab小波工具箱中的cwt( )、scal2frq( )、imagesc( )等函数，其步骤为：首先确定小波基和尺度，并利用cwt( )求小波系数coefs，然后用scal2frq( )将尺度序列转换为实际频率序列f，最后结合时间序列t，用imagesc(t,f,abs(coefs))画出小波时频图。

1.3 MobileNetv2轻量级卷积神经网络

自从2006年Hinton等[31]在《Science》上首次提出深度学习的概念，深度神经网络的表征学习能力得到了广泛关注。在深度学习领域中，已经验证的典型成熟算法有卷积神经网络(CNN)、循环神经网络(RNN)、生成对抗网络(GANs)、深度强化学习(RL)等。其中CNN是深度学习最为典型的网络模型，一般由卷积层、池化层和全连接层等组成，CNN通过构建多个能够提取输入数据特征的卷积核，结合稀疏连接、权重共享、空间或时间上的降采样，对输入数据进行逐层卷积及池化，逐级提取隐藏在数据之中的拓扑结构特征。

然而，经典的CNN由于模型参数和运算量庞大，分析时需要占用大量的存储空间且对计算机硬件要求高。在工程应用中，很多设备(如移动、嵌入式设备)的计算能力和存储空间都很有限，难以运行这样的模型，不利于CNN技术的工程普及。为了能够让深度网络适应这些设备，2017年，Howard等[32]提出了轻量级CNN网络MobileNetv1。MobileNetv1的核心层使用了一种称之为Separable Convolution的操作来替代传统的标准卷积，该网络在保证计算精度基本不降低(或小幅降低)的前提下大幅减少模型参数与运算量。2018年，Sandler等[33]又进一步提出了MobileNetv2。MobileNetv2网络在卷积过程中使用了一种名为Inverted Residuals and Linear Bottlenecks的结构，如图1所示，解决了上一版本中Separable Convolution存在的输入层Kernel数量固定的瓶颈，而且模型更小，准确率更高。

图1 MobileNetv2卷积过程Fig.1 Convolution process of MobileNetv2

本文采用的网络结构模型为MobileNetv2模型，如表1所示。

在表1中，扩展因子用于调整输入图像的大小，同一序列中的所有层具有相同的输出通道数，除第一层外，其他层的步长为1；所有空间卷积使用3×3的核。

表1 网络结构模型Table 1 Network structure model

1.4 基于小波时频图与MobileNetv2的螺栓松动识别方法

基于小波时频图与MobileNetv2的螺栓松动识别方法结构图如图2所示。该方法分为训练和测试两个阶段，训练阶段是利用传声器采集足够数量的螺栓松动声音信号和环境噪声信号，通过信号处理方法提取声音信号的小波时频图作为输入，利用设置好参数的MobileNetv2进行训练得到螺栓松动识别模型。测试阶段则是利用训练好的模型对输入的未知信号进行识别。

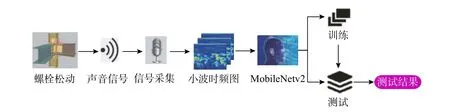
图2 小波时频图- MobileNetv2螺栓松动损伤识别方法结构图Fig.2 Structural diagram of bolt loosening damage identification method based on wavelet time frequency diagrams and MobileNetv2

2 钢桁架试验

2.1 试验简介

试验模型为一位于室外地坪上的正六边形钢管塔架结构，如图3所示。模型边长为1.5 m，高度为6 m，共四层，底层距离地面高度为0.5 m，其余三层高度为1.8 m。塔身立柱采用直径为16 cm的Q235无缝钢管，所有的水平杆件和斜杆均采用等边角钢L40×4，各杆件端部与立柱节点板间采用2个M20螺栓连接(如图3(a))，每根立柱与地面采用四个地脚螺栓连接。模型每层有6个节点，4层共计24个连接节点。为便于下文分析，对各节点统一编号，如图3(b)所示，如Ji4表示第i层第4个节点。

本试验数据采集系统由拾音设备、数据采集设备及计算机组成。拾音设备为放置于模型底部中心位置的8个麦克风组成的环形麦克风阵列，阵列直径20 cm，距地面20 cm。麦克风采用MPA416全指向性麦克风，数据采集模块采用PXI动态信号测试分析仪，如图3所示。

试验步骤如下：

步骤1：损伤工况、噪声工况及复杂工况的模拟。通过松动不同位置、不同数量以及不同程度的螺栓，模拟10种损伤工况，如表2所示。通过一放置于J12节点位置处的手机控制的蓝牙音箱(见图3(c))模拟蝉鸣声、音乐声、下雨声和语音4种常见环境噪声工况。通过组合工况6+蝉鸣声、工况6+下雨声构造2种复杂工况。

表2 损伤工况Table 2 Damage cases

步骤2：模型激振。采用小型偏心式激振器进行激振，当测试第1层～第2层节点时，激振器固定于J12与J13节点之间的横杆位置处。当测试第3层～第4层节点时，激振器固定于J32与J33节点之间的横杆位置处，如图3(e)所示。

图3 试验模型及测试系统Fig.3 Test model and test system

步骤3：信号采集。利用PXI动态信号测试分析仪分别采集10种损伤工况、4种噪声工况以及2种复杂工况共计16种工况的声音信号，信号采样频率为20 kHz。

2.2 声音信号小波时频分析

对采集到的各工况声音信号进行分帧、加窗处理，并分析其短时能量。分帧的帧长取1024点，帧移取512点，加汉宁窗。采用Complex Morlet进行连续小波变换，其中带宽参数和小波中心频率均取3，尺度序列长度取256。

图4～图6分别给出了时长为1 s的蝉鸣声、下雨声、工况6声音信号的典型波形图和相应的38帧短时能量分布图，以及利用短时能量最大的信号帧分析得到的功率谱图和小波时频图。从图4～图6的功率谱图可以看出，三类信号的频率成分非常丰富，其中蝉鸣声频率主要分布在2000 Hz附近和3000 Hz～4000 Hz，下雨声主要分布在1000 Hz～3000 Hz，而螺栓松动声音的频率在0 Hz～4000 Hz均有分布。因此，很难根据功率谱图的特征识别各工况下的声音信号。

图4 蝉鸣声信号图及短时能量最大帧的分析结果Fig.4 Cicada sound signal diagram and analysis results of frame with the largest short-time energy

图5 下雨声信号图及短时能量最大帧的分析结果Fig.5 Rain sound signal diagram and analysis results of frame with the largest short-time energy

图6 工况6信号图及短时能量最大帧的分析结果Fig.6 Signal diagram of Case 6 and analysis results of frame with the largest short-time energy

与功率谱图不同，小波时频图显示了信号频率成分随时间的变化。小波时频图通过冷暖颜色反映信号各频率成分携带的能量大小，颜色越暖能量越大。从图4～图6中可以看出，三种信号的小波时频图暖色部分大多呈现不规则块状分布，且沿时间轴的颜色变化也十分复杂。这样的时频图很难通过人工判断或常规的模式识别方法找出其规律，从而辨别各工况下螺栓松动声音信号。对此，轻量级卷积神经网络MobileNetv2可以发挥其强大的图像分类功能。

2.3 数据集构造

数据是深度学习的“原材料”，学习结果的好坏与数据的规模和质量密切相关。对本文设定的16种工况声音信号重复实测3次，依次对麦克风接收到的声音信号进行分帧、加窗预处理，根据短时能量大小选择特定数目的信号帧，进而进行小波时频分析构造数据集。本文在进行数据集构建时每一工况选取的典型信号时长为15 s，经分帧后共计有584帧信号。去除短时能量低于某一特定阈值的信号帧，选择短时能量偏大的500帧信号进行小波时频分析获得其小波时频图。将每一个小波时频图作为一个样本，可以得到一个由500个典型样本构成的数据集。

图6展示的是工况6采集到的一段时长为1 s的声音信号，其中前半部分为激振器信号(含弱环境干扰)，后半部分为螺栓松动信号。从图6中可以看出，激振器信号的短时能量(约为0.2)要明显小于螺栓松动信号。因此，为了排除激振器信号对最终结果的影响，提高分析效率，本文取一个稍微偏大的预警阀值T=0.5，即仅选择T≥0.5的信号帧进行小波时频分析。

对16种工况声音信号分析得到的各小波时频图进行归类并标注，其中10种损伤工况依次用A～J表示，4种噪声工况用K～N表示，2种复杂工况用O和P表示。每个数据集按照8∶1∶1的比例随机划分出400个样本作为训练集，用以训练模型参数。50个样本作为验证集，用来对模型的参数进行调优并初步评估模型的准确性，剩余的50个样本作为测试集，用于评价模型的泛化能力。因此，最终构造的数据集为8000个样本，其中训练集样本为6400个，验证集和测试集样本各为800个。

3 模型训练

MobileNetv2卷积神经网络在训练时需要设置的参数主要有BatchSize、learning_rate、Dropout、Epochs、num_classes等。综合考虑训练集样本特征和大小、计算机硬件水平、网络结构的深度和复杂度等因素，设定BatchSize为32、learning_rate为0.0005、Dropout为0.2、Epochs为100、num_classes为16、损伤函数采用交叉熵(Cross-Entropy)损失函数。MobileNetv2模型运行的计算机平台及编程环境如表3所示。

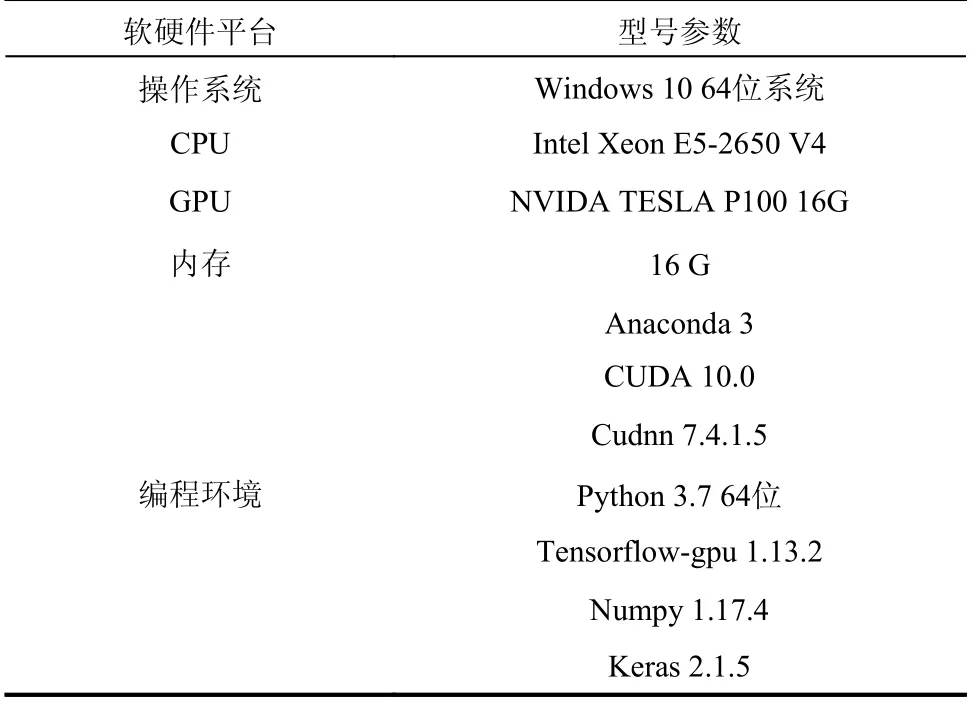
表3 计算机平台及环境配置Table 3 Computer platform and environment configuration

图7展示了当输入模型的样本帧长分别取128、256、512、1024和2048时，训练集和验证集的准确率(Accuracy)和损失值(Loss)随着迭代次数(Epochs)的变化曲线图。从图7中可以看出，当帧长在1024以内时，样本的帧长对模型训练结果影响较大，帧长越长，模型的准确率越高，收敛速度越快，识别结果越稳定，相应最终损失值越小；而当帧长大于1024时，其改善效果不再明显。因此，帧长设定为1024。

图7 样本帧长对MobileNetv2模型识别结果的影响Fig.7 Influence of sample frame length on recognition results of MobileNetv2 model

从图7中还可以看出，当迭代次数在20以内时，训练集和验证集的准确率曲线和损失值曲线都变化较快；当迭代次数位于20和50区间时，其曲线变化速度明显放缓；而当迭代次数大于50时，曲线变化则基本趋于稳定。如图7中帧长为1024的情况，当迭代次数为1～20时，其训练集准确率由63%提高到99%，损失值由1.06降为0.03，验证集准确率由92%提高到99%，损失值由0.23降为0.0004；而当迭代次数等于100时，两类准确率均达到100%，损失值则趋近于0。

此外，本文还将MobileNetv2模型的训练结果与AlexNet、VGG16、GoogleNet与ResNet50等经典的图像识别CNN模型的训练结果进行了比较。各模型训练集与验证集的准确率曲线和损失值曲线如图8所示，经100次迭代以后的识别结果如表4所示。

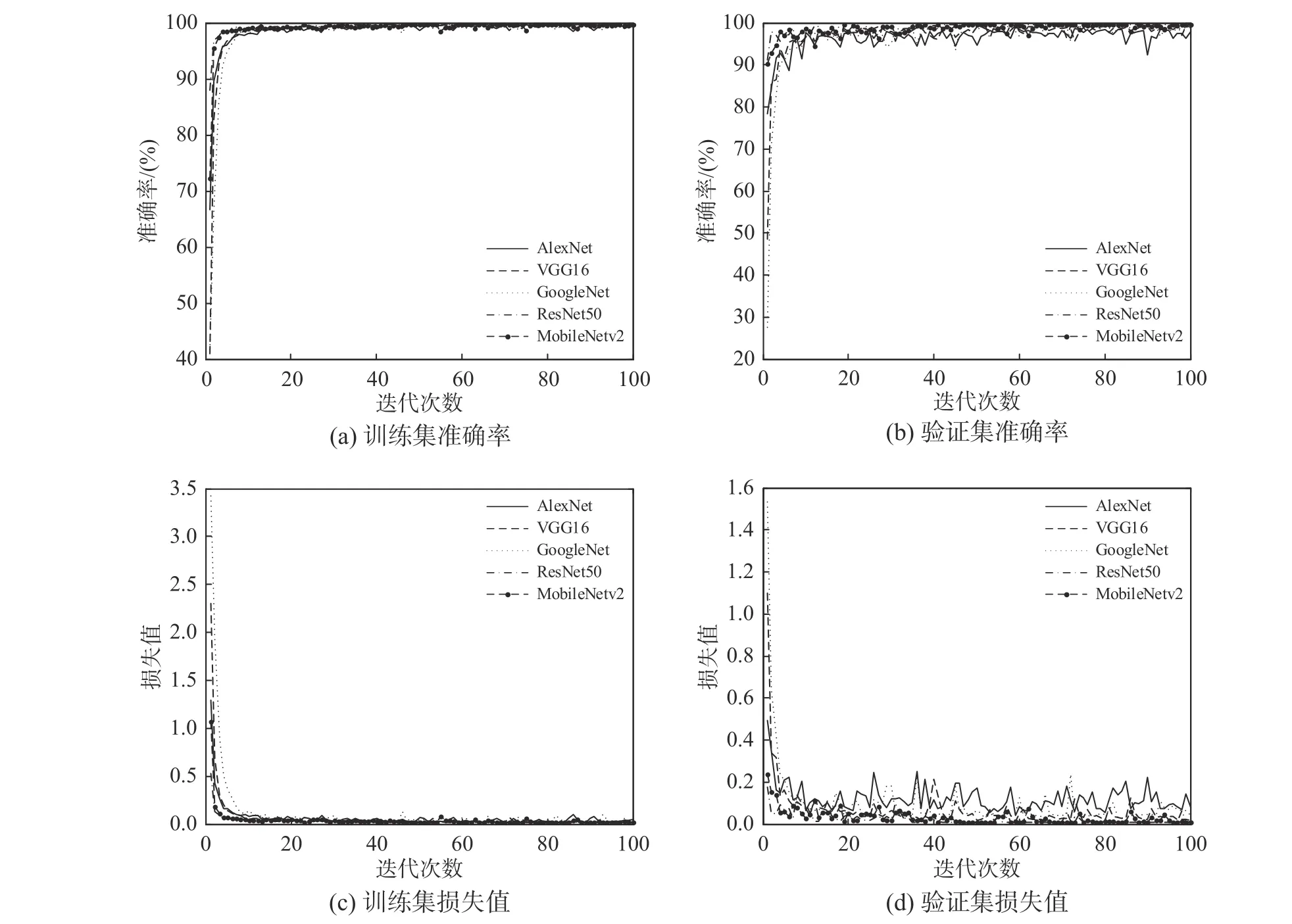
图8 MobileNetv2模型与不同CNN模型的训练结果对比Fig.8 Comparison of training results between MobileNetv2 and other CNN models

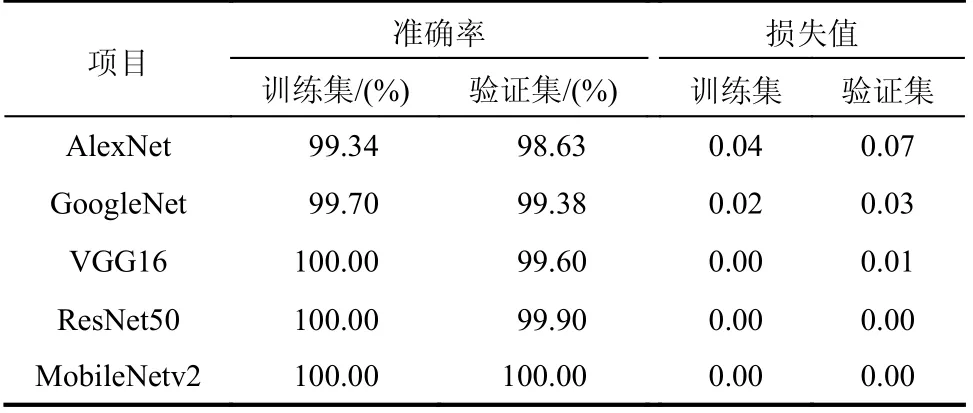
表4 各模型迭代100次的分类准确率和损失值Table 4 Classification accuracy and loss of each model after 100 iterations

从图8和表4中不难看出，MobileNetv2模型与其它4种方法在经过100次迭代以后都已经收敛，其中从训练集和验证集准确率来看，MobileNetv2最好，其最终准确率都达到了100%，ResNet50和VGG16次之，而GoogleNet和AlexNet相对较差，尤其是后者验证集准确率不到99%。从识别稳定性来看，MobileNetv2和ResNet50最好，其识别准确率和损失值曲线除了在少数位置出现波动以外，总体非常稳定。而其它三者相对较差，尤其是GoogleNet和AlexNet出现了较大程度的波动。因此，可以看出，相较于其它几种模型，MobileNetv2无论是在识别准确率还是在稳定性方面的表现都更为优异。

为了考察MobileNetv2模型对计算设备存储的占用情况，本文对比分析了各模型经100次迭代后的总参数量和分析过程生成的权重文件大小，如表5所示。结果表明：MobileNetv2模型的权重文件和总参数量都远远小于其它四类模型的权重文件和总参数量，证明了其在移动设备或嵌入式设备中应用的优越性。

表5 各模型100次迭代后的总参数量和权重文件大小Table 5 Total parameters and weight file size of each model after 100 iterations

4 模型测试

为了检验经过上述训练之后得到的MobileNetv2模型的有效性及泛化能力，采用一组全新的测试集对模型进行测试。测试集的构造方法如2.3节所示。

本文采用混淆矩阵(Confusion matrix)、精确率(Precision)、召回率(Recall)和特异度(Specificity)四个指标来衡量模型对测试样本的分类准确程度[27]，分析结果如图9和表6所示。

图9 混淆矩阵Fig.9 Confusion matrix

表6 分类精确率、召回率和特异度Table 6 Precision, recall and specificity

分析发现，训练得到的MobileNetv2模型对测试样本分类准确率达到99.8%，错误率仅为0.2%。其中，除了标签A、I和N有1个样本，C有2个样本，E有3个样本，J有8个样本被错分到其它类别以外，其它标签的50个测试样本全部被正确识别并分类。通过表6可以看出，尽管标签L对应的50样本全部被准确识别，但由于标签G有2个样本被错分为L，因此，其精确率和特异度分别为0.943和0.996。对于标签C，尽管只有2个样本被错分为I，但由于E有3个样本，I有1个样本，J有2个样本被错分为C，因此，其精确率只有0.873，而召回率和特异度分别为0.96和0.991，以此类推。

上述结果表明：本文所采用的基于小波时频图的MobileNetv2模型不仅能识别不同类型的环境噪声信号，还能很好地区分不同位置、不同数目和松动程度的螺栓松动声音信号。