基于鲸鱼优化算法的配电网故障区段定位

张荣升，刘丽桑，宋天文，邓慧琼，李培强，郑荣进

(福建工程学院 电子电气与物理学院，福建 福州 350118)

配电网的故障区段定位问题一直是电力研究工作者的关注点之一[1]。近年来，分布式电源(distributed generation, DG)因其具有清洁高效等优良特性被广泛应用[2]。例如，利用太阳能、风能建立光伏发电站、风力发电机等功能设备。随着DG在配电网接入规模的加大,传统的单电源网络结构将被打破，由多电源构成的复杂网络结构中，故障电流的流向不再唯一。DG投入与切除、故障电流信息发生畸变以及网络节点规模不断增加等问题对含DG的配电网故障定位提出了新的要求和挑战[3]。本课题根据馈线终端单元(feeder terminal unit, FTU)上报的故障信息对创建的多电源配电网拓扑结构形成的适应度函数求解，利用鲸鱼算法(whale optimization algorithm, WOA)搜索适应度函数的全局最优解，从而实现配电网的故障区段定位。

1 配电网故障定位的原理

配电网故障区段定位利用从FTU传送到配电自动化系统控制中心的故障信息，通过对故障信息进一步判断处理从而发现故障位置，实现故障定位[4]。配电网络被分段开关划分为若干区段，每一个分段开关处均有FTU装置，当FTU中的故障电流大于人工预先设置好的阈值时，系统就会判定其为故障电流，由FTU将故障信息发送到数据采集监控系统(supervisory control and data acquisition, SCADA)，最后通过有效的方法对发生故障的位置进行定位[5]。

由于FTU装置大多安装在户外，易受到自然环境的影响，如雷电打击、风雨冲蚀，或是设备自身的老化故障，从而影响FTU传送故障信息。因此基于智能算法的高容错性，选择一个计算准确、收敛速度快的算法尤为重要。

对传统配电网故障定位原理的分析是实现多电源配电网故障区段定位的前提[6]。本研究首先从配电网区段状态编码、节点状态编码、开关函数构造、适应度函数选择等方面开展进一步研究，建立含有多个电源的配电网络模型，为含分布式电源的配电网故障定位方法的研究提供理论依据[7]。

2 含DG的配电网故障定位模型

2.1 故障信息编码

将断路器、联络开关、分段开关定义为配电网模型中的开关节点，在构造的配电网模型中分别用CB、L、k表示。由于在多电源的配电网中，潮流是双向流动的，因此根据开关节点与电源的距离进行分类，开关节点距离电源较近的区段称为上游区段，开关节点距离电源较远的区段称为下游区段，此处取上游区段为参考方向[8]。

设Ij为开关节点状态的实际量测值，定义参考方向为系统主电源流向分布式电源或负荷的方向，并对每一个开关节点进行编码。当FTU监测到的过流与该节点定义的参考方向一致时，令Ij=1；反之，Ij=-1；如果故障信息没有被检测到，则令Ij=0。这种新建立的编码方式在含分布式电源的配电网故障定位中完全适用[9]。

2.2 开关函数的构造

为了确立开关节点与故障区段之间的联系，构建配电网的开关函数[10]。开关函数好比是一个载体，将获取的故障信息传送给智能算法，在算法的优化下找出配电网中发生故障的位置。图1为含DG的多源配电网模型。

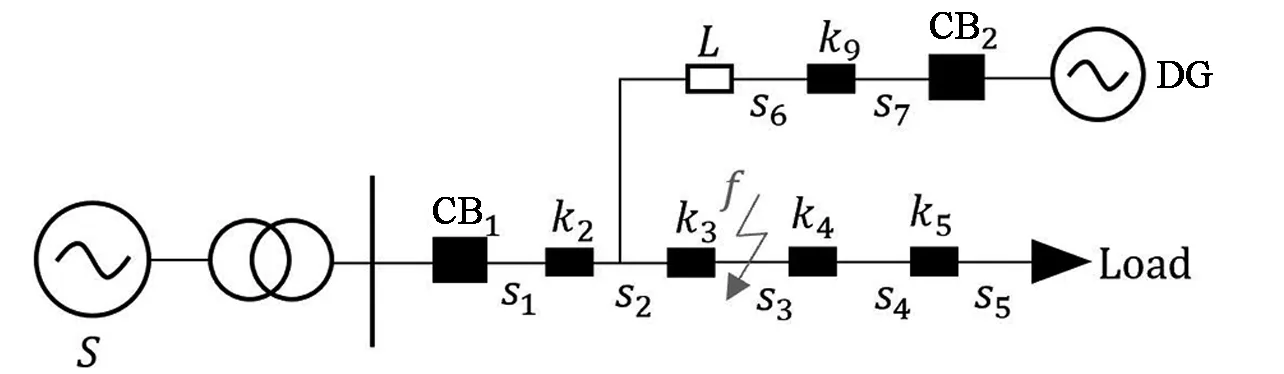
图1 含DG的多源配电网Fig.1 Multi-source distribution network with DG

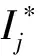
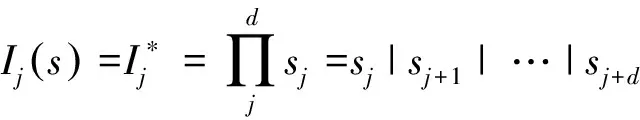
(1)

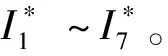
可得系统中所有开关节点的期望值为：

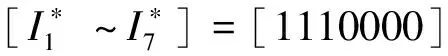
(2)

当s3区段真实发生故障时，各个开关节点状态的实际量测值为：

[I1～I7]=[1110000]

(3)

当断路器CB2闭合，系统由传统的单电源简单配电网转为多电源的复杂配电网模型，此时，当s3区段真实发生故障，各个开关节点状态的实际量测值为：

[I1～I7]=[11100-1-1]

(4)

对比式(3)、式(4)可知，系统中开关节点的期望值与节点状态的实际量测值不同。所以，以往创建的开关函数受限于单电源的简单配电网，不适用于多电源且潮流双向的复杂配电网络则。本研究采用改进后的开关函数适用多电源配电网，如式(5)所示。

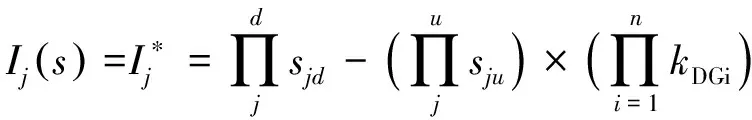
(5)

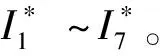
可得系统中所有开关节点的期望值为：

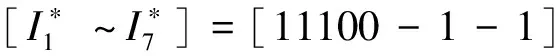
(6)

与式(4)各个开关节点状态的实际量测值一致，因此，式(5)中的开关函数适用于含DG的多源配电网。

2.3 适应度函数的构造

适应度函数通常也被叫作评价函数，是利用智能算法实现故障定位流程中最主要部分。当配电网故障发生时，FTU将故障信息上传至SCADA的实际值和理论推导得到的开关函数期望值进行比较作差。两者之间的差值用适应度函数表示。能否实现配电网故障区段的准确定位取决于适应度函数是否可以准确求解。适应度函数最小值的寻优过程即为应用智能算法实现故障区段定位的过程[12]。

应用智能算法对配电网络进行故障定位的实质就是将所有可能发生故障的区段组成一个解集合，从中找出最能够表达由FTU上传到SCADA的各个开关的故障信息的一条或多条区段，即定位到故障区段[13]。利用这一原理和前文提出的开关函数，构造出如下改进后的适应度函数。

(7)

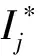
3 鲸鱼算法的基本原理

鲸鱼优化算是2016年提出的一种比较新型的群智能优化算法，该算法全局搜索能力强、计算过程简单、参数设定少，主要包含初期搜索猎物、群体包围猎物和螺旋气泡网捕食3个阶段[15]。

3.1 搜索猎物

鲸鱼优化算法中，可行解x表示参与捕猎行为的每一头鲸鱼。在搜索猎物阶段，基于鲸鱼群体捕猎时的随机游走机制，鲸鱼个体根据群体中彼此的位置信息更新下一代位置，随机搜索使算法具备全局寻优性能。根据第t次的搜索行为，当|A|>1时，鲸鱼对第t+1次的搜索行为进行更新，表述如下:

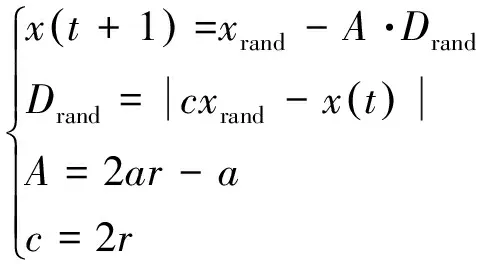
(8)

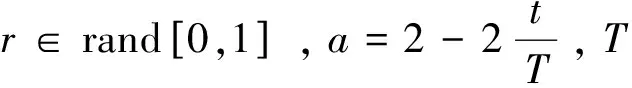
3.2 包围猎物

随着迭代次数的增加，|A|减小至 1，算法进入包围猎物阶段。由于最初搜索时猎物位置不够明确，WOA算法假设将猎物位置或已逼近目标猎物的位置作为此时鲸鱼群中适应度值的最优解，当前最优解的位置信息影响其他鲸鱼进行位置更新，通过逐步包围收缩，接近猎物并确定目标位置。

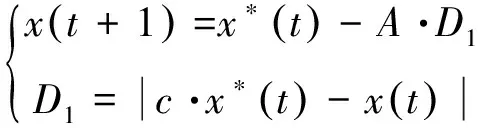
(9)

式中,x(t)为每次迭代的最优解，当A∈rand[-1,1]时，x(t+1)从x(t)向x*(t)迭代更新，逐渐靠近包围最优解。

3.3 螺旋气泡网狩猎

一边吐气泡一边进行螺旋式上升游动是鲸鱼独特的狩猎策略，用这种方式将猎物包围并将其逼近海洋表面，以最佳方式捕获猎物。用以下数学模型可表述这种罕见捕猎行为:

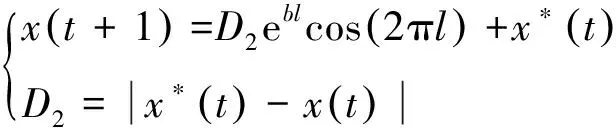
(10)

式中,b为螺旋方程的常量系数，取b=1，D2表示被搜索的个体与当前最优解之间的距离，l∈rand[-1,1]。为了模拟鲸鱼同步进行包围收缩和螺旋气泡网狩猎的围猎行为，设置随机概率对位置更新策略进行选择。在不断逼近目标的迭代过程中|A|持续减小，当|A|=0时,鲸鱼优化算法找到理论最优解。整体围猎机制描述如下:

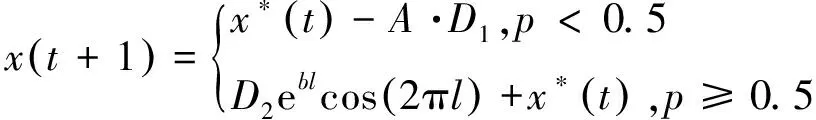
(11)

当随机概率p≥0.5时，鲸鱼群进行气泡网螺旋式捕猎位置的更新，以边吐气泡边螺旋游走的方式逼近猎物，当随机概率p<0.5时，鲸鱼群根据当前最优解的位置进行包围式捕猎位置的更新。

4 算例仿真分析

为了校验鲸鱼算法在配电网故障定位中的有效性和准确性，针对所建立的配电网故障定位模型及其求解方法，在MATLAB R2020b环境下编写程序。计算机系统配置为Intel(R) Core(TM) i7-7660U处理器，CPU2.50 GHz，内存8.00G, Windowsl0操作系统。如图2所示，建立含DG的配电网故障定位仿真算例。

图2中CB1～CB4、L1～L4、k2～k32为均含有FTU装置的开关节点，对应s1～s32的馈线区段，DG1～DG3为分布式电源，并选择性投入运行。对含DG的IEEE标准33节点配电网分别对单点故障定位、多点故障定位以及容错性等方面进行仿真分析，仿真结果如表1所示。

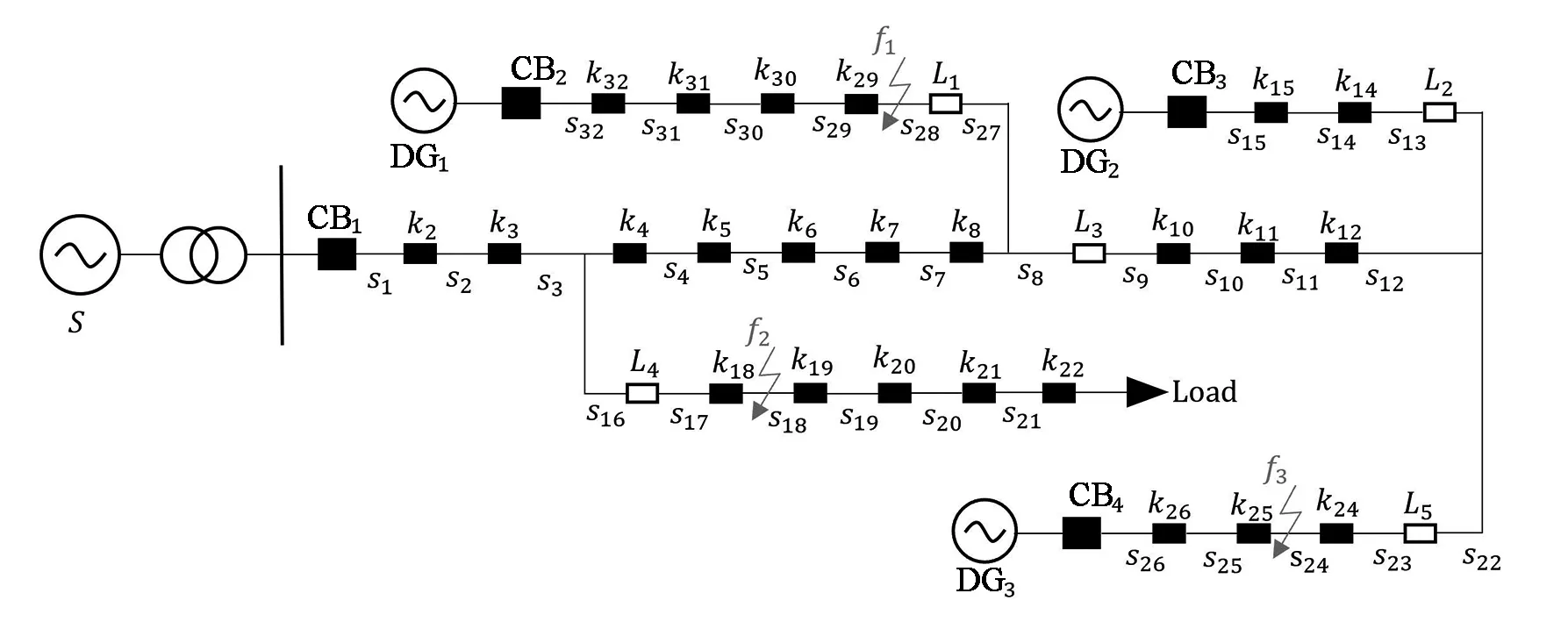
图2 IEEE-33节点配电网拓扑图Fig.2 Topology diagram of IEEE-33-node distribution network

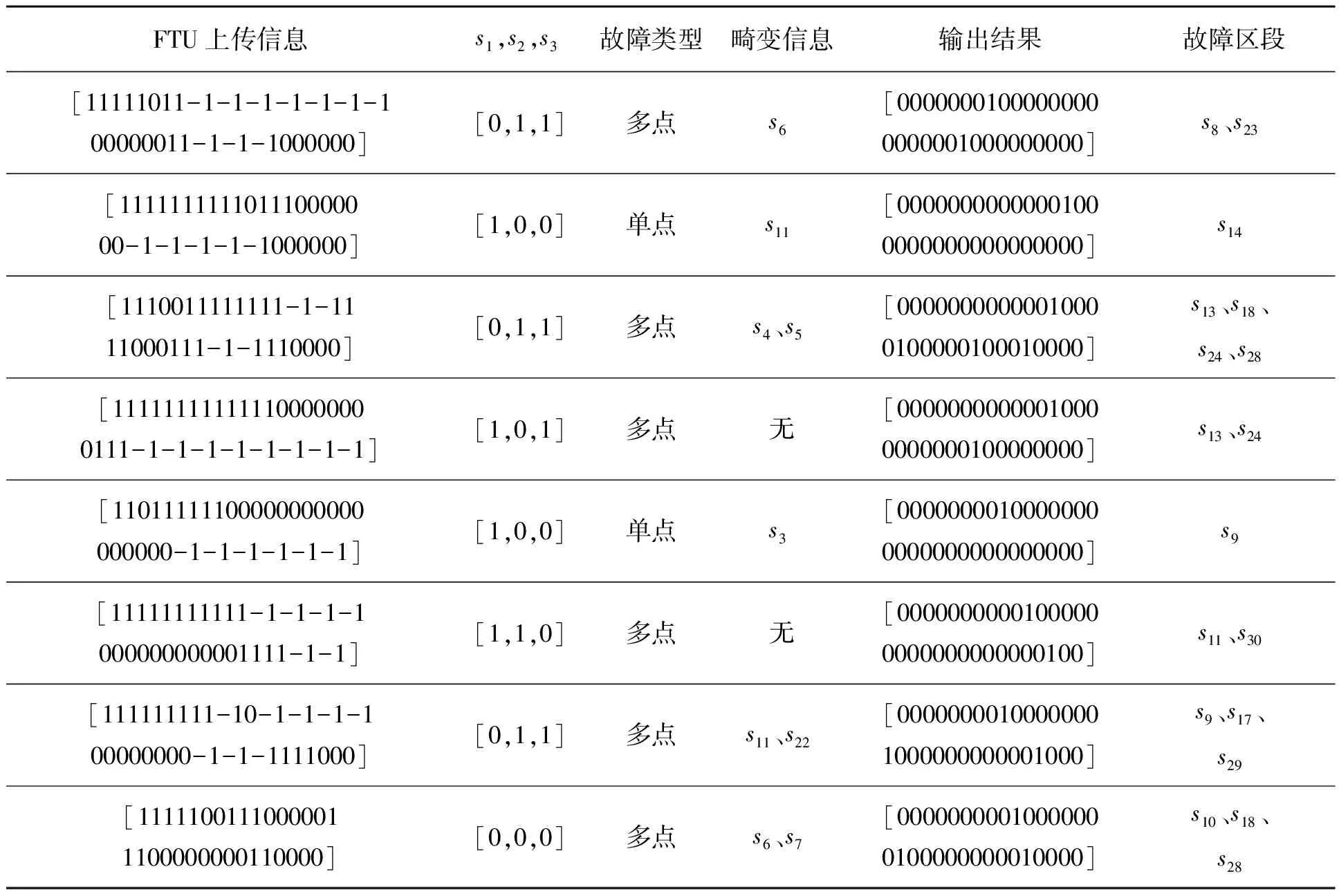
表1 配电网故障定位仿真结果

4.1 单点、多点故障定位分析

在如图2所示的配电网拓扑图中，信息未发生畸变的情况下，用MATLAB 2020b仿真故障定位过程。假设s6馈线区段发生单点故障，3个分布式电源全部接入，FTU上传的信息值为[111111-1-1-1-1-1-1000000000-1-1-1-1-1-1-1-1-1-1-1]，运行主程序，运行结果显示故障区段为s6，并且同时输出定位结果为[00000100000000000000000000000000]，通过仿真可验证该程序可以实现故障区段的准确定位。进行多次单点故障定位仿真，可见该算法优化过程中收敛速度快，准确性高，鲸鱼优化算法的寻优曲线如图3所示，F为适应度函数值(表示数值大小，无单位)，I为迭代次数。

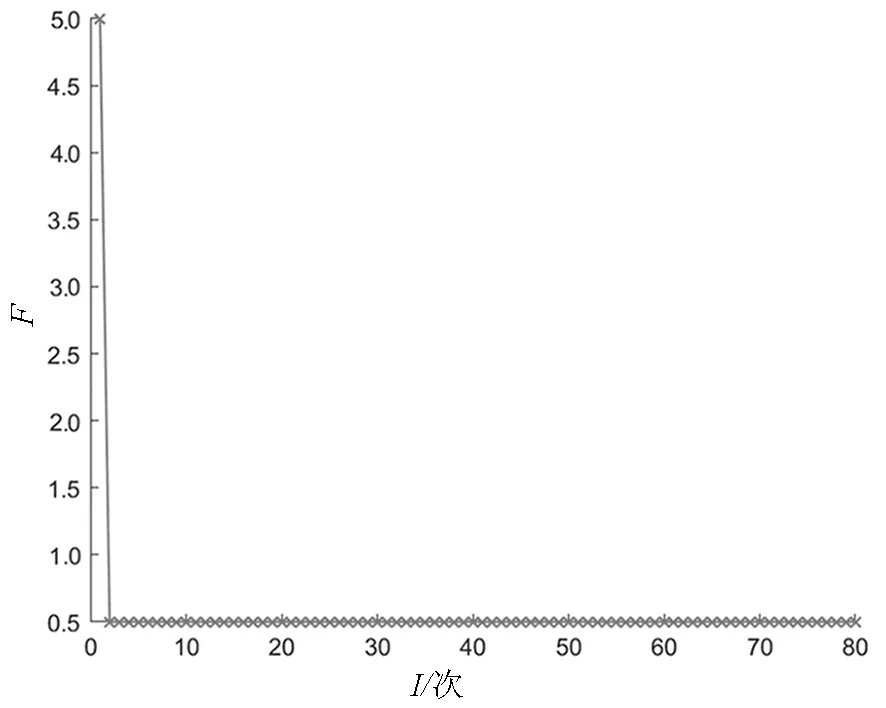
图3 单点馈线区段故障定位收敛曲线Fig.3 Convergence curve of fault location in single feeder sections

s13、s24馈线区段多点故障下，通过仿真可以看出该算法在第5次迭代中出现局部最优的情况，对应的适应度值为6.0，在第8次迭代中达到最优，最优适应度值为3.5。在多次仿真后，通过对比分析发现在发生单点故障时，鲸鱼优化算法计算速度快，而且收敛曲线没有出现局部最优情况；在发生多点故障时，虽然出现局部最优解，但仍然可以在极少的迭代次数之后达到全局最优解，收敛速度相对较快。

4.2 FTU上传故障信息畸变

利用智能算法计算故障点与矩阵法相比最大的优点就是具有良好的容错性。矩阵法编程简单、运行速度快，但故障信息发生畸变或缺失时，会直接导致错误判断。当FTU上传的故障信息发生畸变时，假设s13、s18、s24、s28馈线区段发生多点故障，分布式电源DG2、DG3同时投入运行，FTU上传的故障信息值为[1110011111111-1-1111000111-1-1110000]，s4和s5区段的信息均由“1”畸变成“0”，运行程序，输出结果[00000000000010000100000100010000]，显示故障区段为13、18、24、28。鲸鱼算法具有较高的容错性，可以剔除畸变信息的干扰，并且准确定位到故障区段。图4为上传的故障信息发生畸变的情况下，s13、s18、s24、s28馈线区段多点故障下鲸鱼算法优化过程收敛曲线图，从图中可以看出该算法在第2次和第5次迭代中均出现局部最优的情况，在第7次迭代中达到最优，对应的最优适应度值为0.5。对比发现对于多点故障定位，鲸鱼算法优化过程易陷入局部最优，但收敛速度相对较快，还需对该算法进行优化，提高全局寻优能力。

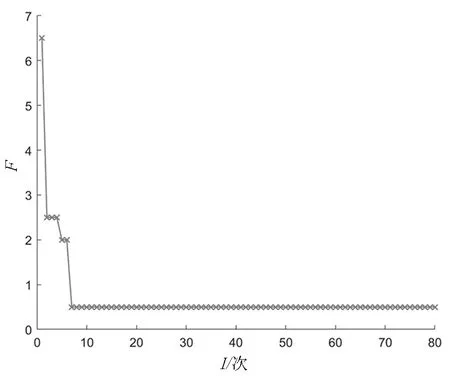
图4 多点馈线区段故障定位收敛曲线Fig.4 Convergence curve of fault location in multiple feeder sections

4.3 不同算法寻优曲线分析

为了检验鲸鱼算法的有效性和优越性可适应于配电网不同故障情况下准确定位，对配电网系统发生单点故障、多点故障、故障信息畸变或缺失等多种情况下分别进行相应的多次仿真分析。并与蝠鲼觅食算法(manta ray foraging optimization, MRFO)、粒子群算法(particle swarm optimization, PSO)、遗传算法(genetic algorithm,GA)进行对比分析。在仿真过程中发现，故障信息未发生畸变的情况下，鲸鱼优化算法在单点故障定位的优化过程中没有陷入局部最优中，最先达到全局最优解，可靠性强。优化过程收敛曲线图如图5所示。

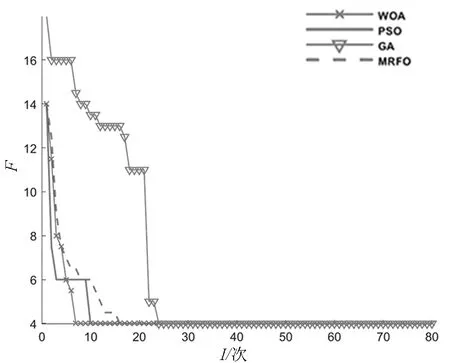
图5 单点故障无信息畸变收敛曲线对比图Fig.5 Comparison diagram of convergence curve without information distortion for single point fault

图6为4种算法在多点故障及故障信息发生畸变的情况下优化过程收敛曲线图，4种算法寻优过程中前期均陷入了局部最优中，但鲸鱼优化算法初始寻优效率高，能够在短时间内得到全局最优解，而蝠鲼觅食算法、遗传算法以及传统粒子群算法陷入局部最优时间较长，收敛速度相对较慢。通过对比分析可知鲸鱼优化算法的计算效率更高，寻优速度更快。

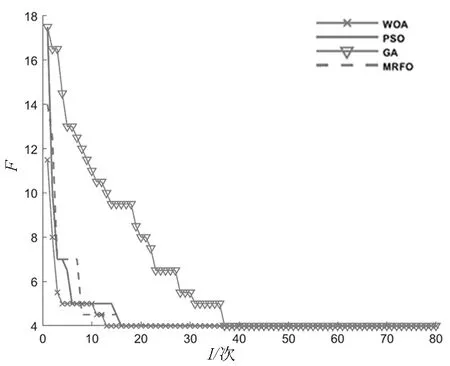
图6 多点故障有信息畸变收敛曲线对比图Fig.6 Comparison diagram of convergence curve with information distortion for multi-point faults

5 总结

通过建立含多个电源接入的配电网故障定位模型，引进基于鲸鱼优化算法的求解方法，通过在多种不同故障情况下对配电网故障定位仿真实例对比分析，结果表明鲸鱼算法在配电网故障定位中相比传统的粒子群算法、遗传算法和以及蝠鲼觅食算法抗干扰性更强，且优化速度更快，收敛性能更强。

分析过程中也发现了鲸鱼算法的不足之处，当配电网发生伴有故障信息畸变或缺失的多点故障时，鲸鱼优化算法在寻优过程中会陷入局部最优中。然而，实际生活中多出故障同时发生的机率小，因此该算法工程实用性相对良好。在今后的科研学习中还需加强对算法的优化，提高其全局收敛性能，从而实现更快速，更准确的配电网故障定位。