基于安全系数法 地铁暗挖通道施工可靠性分析

吴波，吴兵兵

(1.东华理工大学土木与建筑工程学院，江西 南昌 330013；2.广西大学土木建筑工程学院，广西 南宁 530004)

地铁建设是一个庞大而复杂的工程，具有造价高昂、建设周期长、施工难度高、施工人员作业环境恶劣和工程问题复杂的显著特点。综合表现为施工可靠性受诸多潜在风险因素影响较大，一旦发生事故，将会导致十分严重的损失。因此，对地铁施工可靠性进行量化评价具有重要意义。当前对地铁施工安全量化相关方面的研究主要有，钱七虎院士[1]结合经典的工程事故管理理论提出重点研究地下工程全生命周期的风险管理理论和基于可靠性的风险量化方法，为地下工程风险管理理论体系的构建指明了方向。孙钧院士[2]指出隧道及地下工程建设涉及诸多不确定性因素，不可预知的风险存在于地下工程全寿命周期。从设计阶段、施工阶段到运营阶段，应结合各阶段特点，加强风险管理理论与实践研究，建立科学的风险管理理论体系，使风险管理在实际工程应用中规范化、程序化和标准化。在量化评价地铁施工风险方面，张毅军等[3]将改进的TOPSIS方法运用到地铁施工风险分析及评估模型求解中，改善了传统权重法存在的误差问题和风险衡量因子相乘的稀释效应问题，求得的结果更接近工程实际。郝风田等[4]基于可靠度理论建立了地铁施工风险控制模型，对于施工过程的安全优化有一定意义。刘保国等[5]采用故障树分析法对地铁施工风险因素进行了敏感性分析，确定了不同风险因素对风险事件的影响程度。闫文周、赵文等[6-7]研究了地铁施工多风险因素相互作用，并建立相应的风险评价模型，对地铁施工风险评价具有一定的参考价值。应国柱、张飞燕等[8-9]基于概率分布的叠加模型、层次分析法、熵权法和模糊综合评价模型，评估地铁施工风险，是能够同时考虑主客观因素的定量化风险评价方法。应当指出当前研究存在一些不足和空白，评价结果就指导施工而言不够直观；未见量化评价地铁隧道施工可靠性的相关研究。

本文依托南昌地铁3号线地铁车站出入口通道暗挖工程，建立三维数值分析模型比较论证上下台阶法和交叉中隔壁法(CRD法)施工安全性。基于以上论证基础，提出一种量化评价隧道施工可靠性的计算方法。通过对岩土体力学参数进行随机组合，代入建立的数值模型中，使用有限元强度折减法多次计算得到一组安全系数，之后运用可靠度理论计算通道暗挖施工的可靠度。计算方法概念明确且结果直观，保持有限元模拟复杂问题优点的同时考虑了岩土体力学参数的变异性，评价结果合理可靠。

1 地铁车站浅埋暗挖通道施工可靠性分析模型的确定

1.1 地铁车站浅埋暗挖通道施工极限状态方程

在进行通道施工可靠性分析之前，首先要确定通道施工安全极限状态。地铁工程监控量测技术规程[10]中给出的地铁车站隧道暗挖的沉降控制标准：地表沉降值为3 cm，拱顶沉降值为4 cm，以此作为通道施工安全极限状态。浅埋暗挖通道施工可靠性的主要影响因素为暗挖工法、围岩土体强度，暗挖工法确定之后，考虑到土体力学参数的变异性，土体本构关系采用经典的Mohr-Coulomb强度准则描述，基于概率论与数理统计原理，土体强度指标c、φ和相应的安全系数Fs均为服从特定概率分布的随机变量。

地铁车站浅埋暗挖通道施工极限状态方程定义为Y，当Y>0时处于可靠状态，当Y=0时处于临界状态，当Y<0时处于失效状态，如公式(1)所示:

Y=Fs(m,c,φ)-1

(1)

式中，m表示通道暗挖工法；c为土体黏聚力(kPa)；φ为土体内摩擦角(°)；1为通道极限状态安全系数;Fs(·)为安全系数函数，由数值模拟建立映射关系。

1.2 有限元强度折减法基本原理

强度折减法中的强度折减系数，即在外荷载保持不变的情况下，土体能承受的最大剪应力与外荷载对土体所产生的实际剪应力之比。强度折减法应用于边坡稳定性分析中，对影响土体稳定性最大的黏聚力c和内摩擦角φ进行折减[11]。折减后的抗剪强度参数可分别表示为：

cm=c/Fr

(2)

φm=arctan(tanφ/Fr)

(3)

式中，c(kPa)和φ(°)为土体所能够提供的抗剪强度；cm(kPa)和φm(°)是土体极限状态实际发挥的抗剪强度；Fr为强度折减系数。

有限元强度折减法用于通道暗挖可靠性分析时，与进行边坡稳定性分析有所不同的是安全系数Fs的确定。边坡稳定性分析在数值计算过程中设定不同的强度折减系数Fr，边坡达到临界破坏状态时的强度折减系数即为稳定安全系数Fs。通道暗挖可靠性分析则以通道开挖完成后拱顶沉降和地表沉降达到地铁工程监控量测技术规程给出的安全规范限值作为确定安全系数的极限状态，在数值计算过程中通过在相应的分析步后对围岩土体力学参数进行折减，之后考察此分析步中拱顶沉降发生突变时对应的强度折减系数Fr，将此时的力学参数代入原数值模型中进行通道开挖全过程模拟，若通道处于极限状态，则此时的强度折减系数Fr即为安全系数Fs。

1.3 点估计法基本原理

目前，计算可靠度指标β的实用方法有：点估计法、一次二阶矩法、渐进积分法、随机响应面法和Monte-Carlo法等[12]。一次二阶矩法需用泰勒展开式将分布函数展开，且对取值点附近的局部性质考虑不足，计算产生的误差较大；渐进积分法需对基本变量概率密度函数进行复杂的求导计算，工作量较大；随机响应面法需用到线性无关原则及概率配点法，计算过程繁琐；Monte-Carlo法需进行大量的随机采样，工作量较大[13]。Rosenbleuth1975年提出点估计法，求出随机变量的均值和方差，即可确定状态函数的均值和方差，进而计算出相应的可靠度指标和失效概率。经有关专家学者验证点估计法的计算结果与其他常用的方法较为吻合，是一种实用简便的可靠度计算方法。

对点估计法在通道施工可靠性分析中的应用介绍如下，点估计法不必考虑分布函数的变化形态，直接取随机变量的均值±标准差来构建基本取值点，土体本构关系采用Mohr-Coulomb模型，表达式为：

τ=c+σtanφ

(4)

式中，c为土体黏聚力(kPa);φ为土体内摩擦角(°);τ为土体滑移面上的切应力(kPa)；σ为土体滑移面上的正应力(kPa)。

因此，c、φ值为影响通道施工可靠性的主要因素，构建相应的基本取值点为：

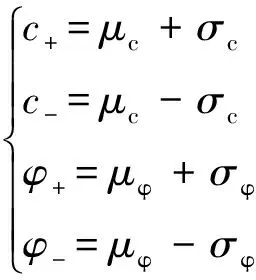
(5)

式中，μc为土体黏聚力平均值(kPa);μφ为土体内摩擦角平均值(°);σc为土体黏聚力标准差(kPa);σφ为土体内摩擦角标准差(°)。

当通道围岩为单一土层，进行通道施工可靠性分析时，运用有限元软件建立数值分析模型，对施工方法m与土体黏聚力c、土体内摩擦角φ的每一组合采用有限元强度折减法进行数值计算，确定相应的安全系数Fs，如式(6)：

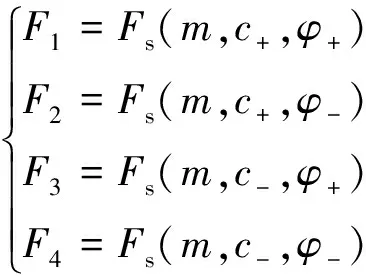
(6)

由公式(7)～(10)计算安全系数Fs的平均值μF、标准差σF、可靠度指标β、失效概率Pf，之后对通道施工可靠性进行评价。

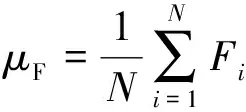
(7)

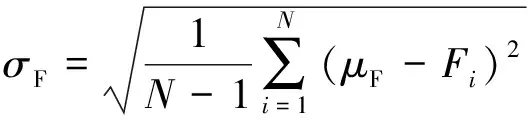
(8)

β=(μF-1)/σF

(9)

Pf=1-Φ(β)

(10)

式中，Φ(x)表示标准正态分布函数，可查标准正态分布表取值。

2 工程实例分析

2.1 工程概况

南昌地铁3号线邓埠站1号出入口通道采用暗挖法施工，通道断面形式为直墙拱顶，通道主体结构覆土厚度约4.2 m。通道开挖宽度为9.8 m，开挖高度为5.9 m，开挖长度为23 m。通道施工范围内主要以软弱土层为主，基底为砂土层。原地面至通道拱顶范围内依次为回填土和粉质黏土，拱顶至通道结构底板顶面范围内为粉质黏土，通道结构底板以下为砂土。暗挖通道结构范围内不存在地下水，地下水位埋深位于结构底板以下约6 m。施工期间不考虑降水问题，仅采取施工场地地面排水措施。图1所示为暗挖通道范围地层分布图。

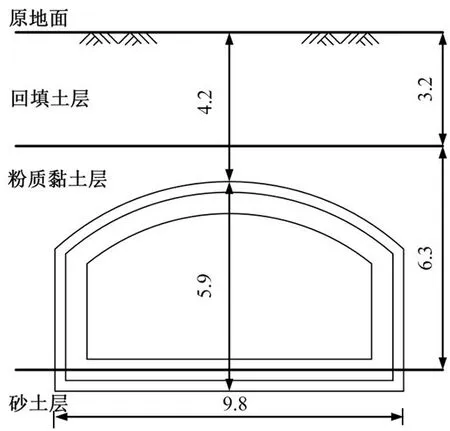
图1 暗挖通道范围地层分布图(单位：m)Fig.1 Stratigraphic distribution map of the range of underground tunnel(unit: m)

2.2 模型参数选取

土体力学参数的选取对数值模拟结果合理性有很大的影响，根据工程地质勘察资料土工试验报告和工程设计资料确定模型参数如表1所示。初期支护与二次衬砌的力学参数均根据工程设计值，与工程实际保持一致。土体本构关系采用摩尔-库仑模型模拟，初期支护及二次衬砌采用弹性模型模拟。

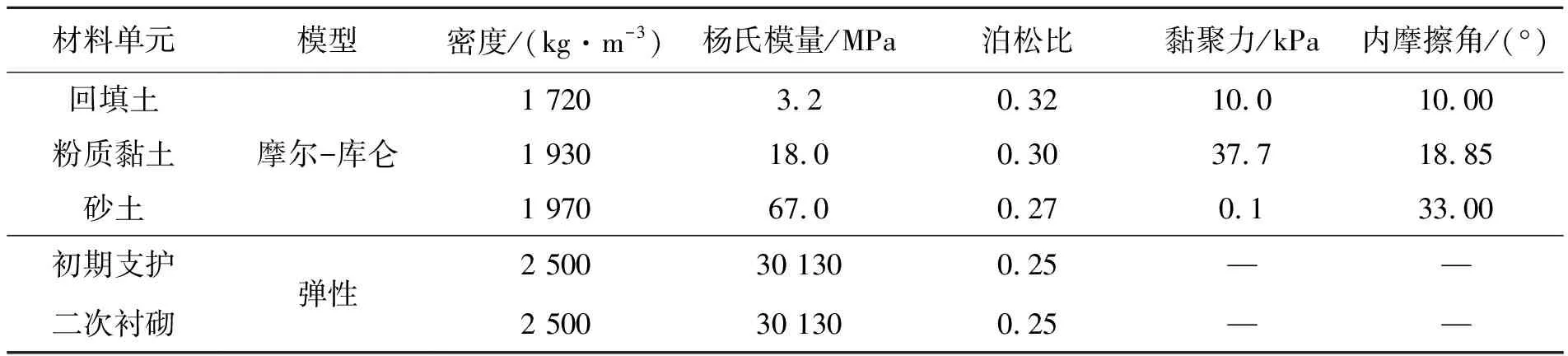
表1 模型参数

2.3 数值分析模型建立与计算

根据圣维南原理，通道开挖方向即纵向与实际尺寸一致，通道埋深与实际尺寸一致，通道左右和下方土体尺寸分别取通道开挖宽度和开挖高度的3倍。采用ABAQUS软件对通道暗挖施工进行数值模拟，首先建立横向、纵向和竖向尺寸为68 m×23 m×27 m的土体模型，之后创建初期支护和二次衬砌部件，在装配模块中将土体、初期支护和二次衬砌装配成一个整体，构建真实的几何及物理关系。创建相应分析步，在接触模块中采用单元的激活和抑制功能模拟真实开挖工序。在初始分析步中设置模型边界条件，对整个模型施加重力载荷，对模型前后、左右及底部施加法向位移约束。划分网格，提交作业计算。图2所示为计算模型示意图。

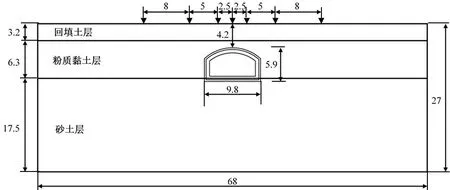
图2 计算模型示意图(单位：m)Fig.2 Schematic diagram of calculation model(unit: m)

实际工程地表沉降监测点由通道中轴线正上方向左右两侧布置，总共布置7个监测点在图2中标出。

计算工况分别为上下台阶法施工与交叉中隔壁法施工，上下台阶法施工将整个开挖断面分为上、下两部分，开挖步距为2 m，上台阶开挖后立即施作初期支护和临时仰拱封闭成环，开挖下台阶时移除上部临时仰拱，整个通道开挖完成且初期支护施作完成之后进行二次衬砌施工，工序示意图如图3(a)所示。交叉中隔壁法施工将整个断面分为4部分开挖，依次为左上导洞、左下导洞、右上导洞和右下导洞；开挖步距为左上导洞与左下导洞保持4 m的安全施工距离，左下导洞与右上导洞保持4 m的安全施工距离，右下导洞与右上导洞保持4 m的安全施工距离。导洞开挖进尺2 m，每循环进尺后立即施作初期支护封闭成环，按照施工步距循环进尺开挖，直至整个通道开挖完成，拆除中隔壁，施作二次衬砌。工序示意图如图3(b)所示。数值计算完全模拟实际施工工序。

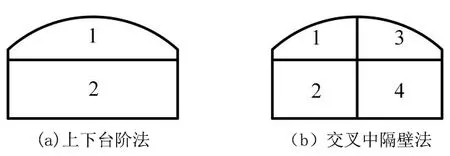
图3 工序示意图Fig.3 Schematic diagram of working procedure

3 结果与分析

3.1 通道施工数值模拟结果分析

3.1.1 上下台阶法施工分析

上下台阶法施工数值模拟结果显示通道最大拱顶沉降值为7.5 cm，如图4所示；通道最大地表沉降值为5.2 cm，如图5所示；与规范控制值相比较显然无法满足要求。拱顶沉降规律与地表沉降一致，表现出通道正上方地表沉降最大，距通道正上方越远，受开挖影响越小，地表沉降值呈逐渐减小趋势。距离中轴线15 m左右，地表沉降值可忽略不计。

图4 上下台阶法沉降云图(单位：m)Fig.4 Settlement cloud map of up-down step method (unit: m)

图5 上下台阶法地表沉降曲线Fig.5 Surface settlement curve of up-down step method

围岩为软弱土层时，不应采用上下台阶法开挖隧道。城市地铁隧道施工对地表沉降控制极为严格，由此应采用其他暗挖工法，确保施工安全及地表沉降得到有力控制，交叉中隔壁法即为一种有效的施工方法。

3.1.2 交叉中隔壁法施工分析

交叉中隔壁法施工数值模拟结果显示最大拱顶沉降值为3.2 cm，如图6所示；最大地表沉降值为1.6 cm，如图7所示；均在规范控制值以内。最大拱顶沉降位于导洞3正上方拱顶处，最大地表沉降位于通道中轴线正上方偏右。地表沉降和拱顶沉降相较上下台阶法开挖引起的沉降规律有一定差异。因此不同的施工方法对于地层的扰动不一样，但其整体地层沉降规律是相近的。交叉中隔壁法与上下台阶法地表沉降曲线对比如图8所示，相较于上下台阶法施工，地表沉降得到有力控制。针对软弱地层隧道暗挖施工应采用短开挖快封闭的施工方法，能够最大限度地保证施工安全。

图6 CRD法沉降云图(单位：m)Fig.6 Settlement cloud map of CRD method(unit: m)

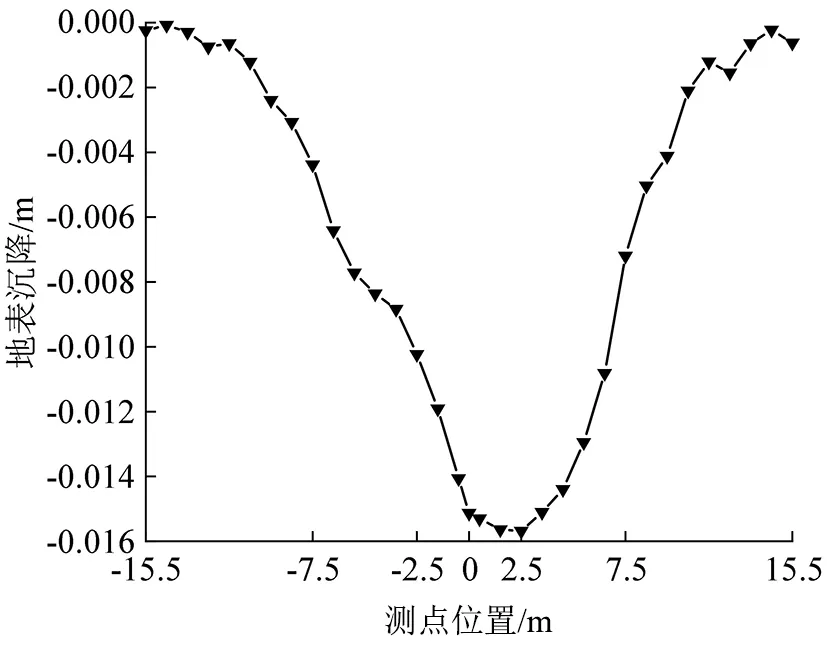
图7 CRD法地表沉降曲线Fig.7 Surface settlement curve of CRD method

图8 地表沉降曲线对比图Fig.8 Surface settlement curve comparison

3.2 通道施工可靠性分析

3.2.1 无风险因素作用下通道交叉中隔壁法施工可靠性分析

上下台阶法开挖无法满足安全施工和控制地表沉降的要求，因此采用交叉中隔壁法进行通道施工，并计算交叉中隔壁法施工可靠度，定量评价交叉中隔壁法施工的可靠性。鉴于土体力学参数存在一定的变异性，精确确定力学参数难以实现，而力学参数对数值计算结果有着很大的影响。通过对工程地勘资料土工试验报告中给出的围岩力学参数平均值及标准差进行组合，在一定程度上能够降低土体力学参数变异性的影响，使数值模拟结果更加接近实际。通道围岩为粉质黏土层，土工试验报告显示其黏聚力平均值μc=37.7 kPa，内摩擦角平均值μφ=18.85°，黏聚力标准差σc=2.13 kPa，内摩擦角标准差σφ=3.22°。根据公式(5)构建力学参数取值为：

将黏聚力c与内摩擦角φ进行组合，其余力学参数保持不变。分别代入数值模型，采用有限元强度折减法计算得到一组安全系数为：

此时，按照公式(7)～公式(10)，安全系数均值μF=1.358，标准差σF=0.122，可靠度指标β=2.93，失效概率Pf=1-Φ(2.93)=0.17%，计算结果表明，通道是稳定的，与3.1.2节的分析结果一致。拱顶沉降和地表沉降均在规范值以内，不会有安全事故的发生。

3.2.2 风险因素作用下通道交叉中隔壁法施工可靠性分析

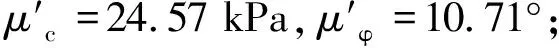
将黏聚力c与内摩擦角φ进行组合，其余力学参数根据表2取值，分别代入数值模型，采用有限元强度折减法计算得到一组安全系数为：

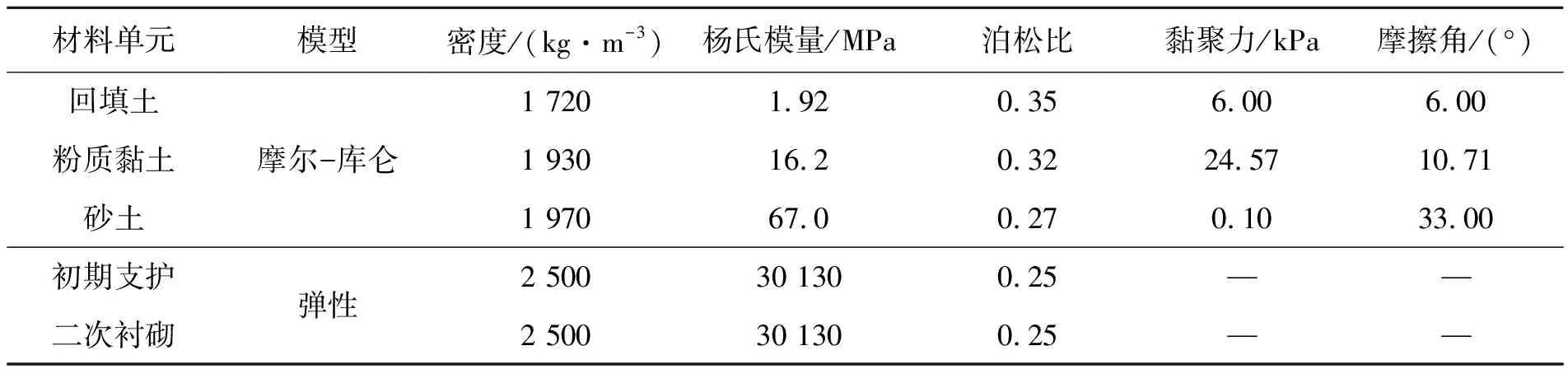
表2 风险因素作用下的模型参数

按照公式(7)～公式(10)，安全系数均值μF=0.838，标准差σF=0.059，可靠度指标β=-2.75，失效概率Pf=1-Φ(-2.75)=99.7%，计算结果表明，通道大概率无法满足安全施工和沉降控制要求。由图9和图10也可以看出，必须在强降雨渗入导致土体强度降低时对通道上方土体进行加固。

图9 风险因素作用下CRD法沉降云图(单位：m)Fig.9 Settlement cloud map of CRD method under the action of risk factors(unit: m)

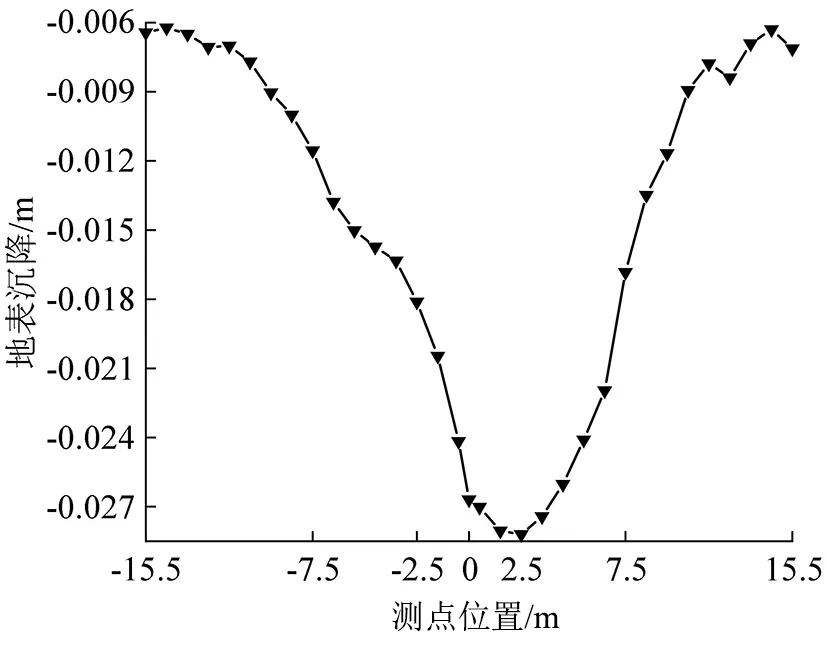
图10 风险因素作用下CRD法地表沉降曲线Fig.10 Surface settlement curve CRD method under the action of risk factors

3.3 现场实测数据对比分析

通道暗挖工程以数值模拟结果作为重要参考并经专家论证，采用交叉中隔壁法施工。图11为通道暗挖工程施工完成后基于现场监测数据所绘制的地表沉降曲线。由图11可以看出，数值模拟结果中对应地表沉降监测点的地表沉降规律与现场实测数据呈现出的地表沉降规律一致。考虑到岩土体力学参数的变异性、实际工程施工的复杂性和施工时空效应等因素影响，实测数据与数值模拟结果差异不可避免。差异在合理值范围内，表明数值模拟结果是可靠的。通道暗挖工程采用交叉中隔壁法施工，保证施工安全的同时能够有效控制地层沉降，交叉中隔壁法施工分析及无风险因素作用下通道交叉中隔壁法施工可靠性分析所得结论与现场实际施工情况一致。

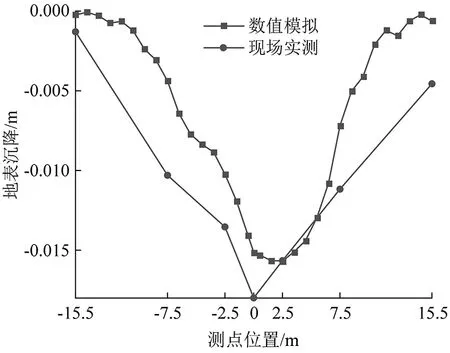
图11 数值模拟与实测数据地表沉降曲线对比图Fig.11 Surface settlement curve comparison between numerical simulation and measured data

4 结论

1)软弱围岩条件下，上下台阶法无法满足施工安全需要和地层沉降控制要求。通道暗挖采用交叉中隔壁法可确保施工安全和有效控制地层沉降，数值模拟结果与现场实测数据呈现出的地层沉降规律一致，并且拱顶沉降及地表沉降均在规范限值以内。通道暗挖施工重点加固通道开挖面正上方土体可有效控制地层沉降，通道开挖完成拆除临时支护时须遵循分段拆除原则，确保施工安全。

2)针对无风险因素作用和风险因素最不利组合作用两种情形下通道交叉中隔壁法施工，提出一种基于安全系数的施工可靠性定量评价方法。采用有限元强度折减法计算相应安全系数，之后采用点估计法计算施工可靠度，可正确评价通道暗挖工程实际施工的安全状态。

3)通道暗挖施工中极端天气风险必须加以关注，文中探讨的强降雨入渗引起通道上覆土体力学参数降低，显著影响施工可靠性，使得拱顶沉降值超过规范限值。值得注意的是通道施工在受降雨入渗作用下，围岩位移特征点有显著的变化，是一个渐进的过程，通过及时分析监测数据和采取相应技术措施可预防风险事件的发生，保证施工安全。