基于VxWorks操作系统的某随动系统控制算法软件设计与实现
2021-09-23刘元元
刘元元
(中船重工第七一三研究所,河南 郑州 450015)
某舰载装置随动系统采用了大功率数字交流伺服系统,为实现装置在大惯量、变负载等复杂工况下具有响应快、稳定性强、精度高的特点,笔者对装置控制算法进行研究设计。
自校正控制是对被控过程参数的在线辨识和控制器参数自动整定相结合的一种控制技术。PID控制器是应用最为广泛的一类控制器,具有直观、容易实现和鲁棒性能良好的一系列优点。将PID控制与自校正控制器相结合形成的自校正PID控制,它具备了两者的优点。首先,它是自校正控制器,具有能自动辨识被控过程参数、自动整定控制器参数、能适应被控过程参数的变化等一系列的优点;其次,它又具有常规PID控制器结构简单、鲁棒性好的优点。该控制法具有的这两大优势,使其成为伺服控制中一种较理想的控制器,成为人们重点研究的对象和自校正控制发展的一个方向[1]。
笔者以军用加固机作为控制系统的硬件平台、嵌入式操作系统VxWorks为软件平台设计了一种自校正PID控制器,根据载弹量变化实时调整PID控制参数,并进行试验验证。
1 VxWorks操作系统简介
VxWorks操作系统于1983年由美国风河公司设计开发,是一种具有良好的持续发展能力、高性能的内核以及友好的用户开发环境的嵌入式操作系统。因其具有良好的可靠性和卓越的实时性,故被广泛地应用在军事、通讯、航空、航天等高精尖技术及实时性要求极高的领域中[2]。
VxWorks系统提供多处理器间和任务间高效的信号灯、消息队列、管道、网络透明的套接字,随动系统软件功能的实现基于中断和任务这两个最基本的执行线程:任务由操作系统内核调度执行;中断由硬件异步触发,执行中断处理代码。本软件基于功能实现划分出了网络通信、随动控制和状态监控,在系统运行中VxWorks会使用优先级抢占调度策略协调多个任务共享CPU[3]。为保证实时性,系统也包含中断处理线程,周期性响应随控定时器中断来激活对实时性有要求的随动控制任务线程。
2 自校正控制器原理
自校正控制系统是一个具有一定适应能力的系统,能够认识环境条件的变化,并自动校正控制动作,使系统达到最优的控制效果[4]。自校正控制的原理框图如图1所示。
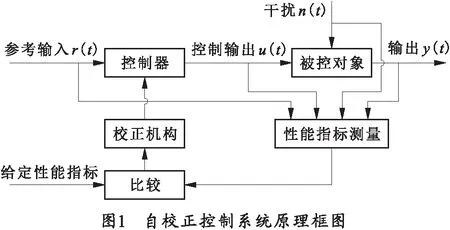
该系统在运行过程中,根据参考输入r(t)、控制输出u(t)、对象输出y(t)和干扰n(t)来测量对象性能指标,并与给定的性能指标进行比较,做出决策,然后通过校正机构来改变系统参数,或者产生一个辅助的控制输入量,累加到系统上,以保证系统跟踪上给定的最优性能指标。与常规PID控制系统比较,自校正控制系统有3个显著特点[5]:
1)控制器可调,相对于常规PID反馈控制器固定的结构和参数,自校正控制系统的控制器参数在控制的过程中一般是根据一定的自校正规则,不断更改或者变化的。
2)增加了自校正回路,该控制器在常规反馈控制系统基础上增加了自校正回路(或称自校正外环),主要作用就是根据系统运行情况,自动调整控制器,以适应被控对象特性的变化。
3)自校正控制方法适应于被控对象特性未知或者扰动特性变化范围很大,同时又要求保持高性能指标的一类系统。
3 随动系统自校正PID控制器设计
3.1 某装置随动系统简介
某型装置具有以下特点:负载为变质量系统,大载弹量、高密度贮存,转动惯量和负载不平衡力矩大,且随导弹的发射而改变,使得系统扰动大,动态特性变化范围广;系统反应时间短,调转速度快,跟踪精度高;系统工作范围宽,方位工作范围达300°,高低角达100°;不同装舰对象的装置结构不同,但随动系统通用。
随动系统采用数字交流随动系统,工作原理是随控计算机实时接收上级武器控制系统发送的目标高低/方向角位置信息,与随动系统位置检测装置检测到的实际位置进行比较,按照规定的控制规律解算得到速度给定控制字,通过D/A接口输出电压信号,伺服驱动器对信号进行功率放大后,驱动电机通过齿轮传动装置拖动发射装置运动到武器控制系统给出的目标高低/方向角位置,在实现对目标角的跟踪过程中满足动态精度要求。工作原理如图2所示。

为了实现装置的快速反应,达到总体技术指标要求,采用了大功率数字交流随动系统,其随动系统关键设备主要包括[6]:
1)执行设备:采用交流永磁伺服电机。
2)驱动设备:采用大功率交流伺服驱动器。
3)控制设备:采用军用加固机,包括CPU板、DA板和SDC板。本软件使用操作系统VxWorks提供的消息队列和信号量等线程间通信机制来实现任务同步以及对临界资源的互斥保护。
4)位置检测装置:粗精双通道自整角机系统,精粗比为12。
3.2 PID控制零-极点对消方法
把控制作用和干扰组成的被控对象模型用受控自回归滑动平均CARMA模型来描述[7],即
A(q-1)y(k)=B(q-1)u(k-k0)+C(q-1)ζ(k),
(1)
A(q-1)=1+a1q-1+…+anaq-na,
(2)
B(q-1)=b0+b1q-1+…+bnbq-nb,b0≠0,
(3)
C(q-1)=1+c1q-1+…+cncq-nc,
(4)
式中:y(k)为系统输出;u(k)为控制量;ζ(k)为系统噪声;k0为系统的滞后步数;na,nb,nc分别为阶次。
增量式PID控制器的结构形式为
(5)
(6)
为了保证闭环稳定,加入一个滤波环节F(q-1):
F(q-1)=1+f1q-1,
(7)
式中:g0,g1,g2为包含PID控制器比例、积分、微分环节的控制参数;f1为滤波系数。
系统闭环结构如图3所示。由于对象是开环稳定的最小相位系统,故可对图3中的前向通道传递函数做零、极点对消处理,即令
(8)
G(q-1)=A(q-1).
(9)

控制器采用零-极点对消PID方法可将系统闭环结构进行简化,如图4所示。

由图4可知,通过上述零-极点对消PID控制设计方法,可得到系统期望的特征多项式。
对于许多控制过程,模型阶次可取为na=2,nb=1。这样,可以方便地使用PID控制参数g0,g1,g2来配置极点,即
(10)
于是,闭环传递函数y(k)就可以简化为
(11)
由式(11)可知,只要b0、g0选择适当,就可以实现期望的闭环极点,同时b0、g0的选取也要满足稳定条件。为保证系统稳定,需满足0 (12) 随着导弹的发射,装置的负载状态从满载到空载发生改变,系统控制环的模型不确定因素为负载变化导致的转动惯量的改变,因此,在自校正PID控制器设计中重要一环是对装置载弹量参数的实时获取,根据与上级武器控制系统的通信协议,此参数可从武器控制系统周期回馈的报文中获得。 某型装置的发射集装箱是筒弹安装、定位、贮存和发射的支架,系统满载载弹量为8枚,即具有9种负载状态,为了简化系统控制,将负载分成3种状态,即空载(0~2枚)、半满载(3~5枚)和满载(6~8枚)。这样分的优点是在载弹量为3枚以下时,筒弹与发射集装箱质量比小于1,折合到电机端惯量变化不超过20%;在3~5枚时,筒弹与发射集装箱质量比小于2;在6~8枚时,筒弹与发射集装箱质量比小于3,这样进行设计既能利于控制,又减轻了控制器的复杂度。 因此,随动系统自校正PID控制器控制算法的研究思路是:装置在满载、半满载、空载工况下其控制对象为确定的模型,分别运用零-极点对消的方法计算3种工作状态下的PID参数,设计的自校正PID控制器就是实现在每个采样周期读取上位机武器控制系统反馈的载弹量,对载弹量进行判断来确定系统所处的工况,当工况发生变化时,实时改变PID控制参数,进而实现系统的自适应控制。 该装置随动系统位置环控制对象开环传递函数可近似表示为 (13) 对其进行带零阶保持器的Z变换,采样周期T取6.25 ms,可得其离散数学模型w(z): (14) 即 (15) 可以得出为系统的滞后步数k0为1,被控对象的CARMA模型为 (1+a1z-1+a2z-2)y(z)= z-1(b0+b1z-1)u(z)+C(q-1)ξ(k). (16) 从零-极点对消的观点出发,系统PID零-极点对消的闭环传递函数如式(11)和控制器输出如式(12)所示。 以满载近似控制对象为例进行零-极点对消办法计算控制量: (17) 将式(17)进行Z变换,其满载控制对象离散模型为 (18) 即b0=0.008 5,b1=0.007 9,a1=-1.781 1,a2=0.781 1。 将其代入式(17)中,可得到系统满载工况下利用零-极点对消的原理设计的闭环传递函数控制输出: (19) 从零-极点对消的观点出发,按“二阶最优”模型,即超调量为4.3%,阻尼比ξ为0.707,依此选取g0。二阶最优模型系统的特征方程对应的离散特征多项式为 (20) 式中: (21) 取NT=10,可计算得出ωn=142。 按照同样的方法,可以计算得出半满载、空载下的控制输出量: 半满载时为 (22) 空载时为 (23) 由于装置不能实现全向运动,在编写控制程序时必须设置大角度调转控制程序。大角度调转控制就是确保设备在极限范围内运转,而不能穿过极限区域外以小角度转到给定角位置。 为了实现大角度运行控制,在控制程序中,引入控制方向iDir这一变量,根据输入角与输出角计算得到偏差角,当偏差角大于0时,iDir被赋值1,控制器输出的控制字大于0,设备正向运动;反之,iDir=-1,设备反向运动。例如,装置当前的位置是在-150°处,要求调转到100°处,从圆周上看,设备穿过极限角到100°,只需运行110°,但是这种运转方式是不被允许的,通过大角度控制就可以避免出现这种情况,控制器通过计算目标角位置和当前角位置的偏差值e(k)大于0,进而规定了装置只能正向运行,就达到了避免设备反向运行超出极限角的目的。因此通过控制器输出控制字的正负之分,规定其运行方向,避免了以穿越极限角的方式运行,确保了装置的安全。其流程图如图5所示。 用C语言编写控制程序,通过Tornado集成环境编译链接生成可引导文件,灌装至加固机中[9],并在装置满载、半满载、空载工况下进行控制算法验证,分别进行了调转及等速跟踪试验[10],通过采集的数据可得到最大动态跟踪误差,由数据生成的运动曲线如图6~11所示。从图6、7中的满载试验结果及试验数据可知,调转50°的时间是1.306 s,最大动态跟踪误差不大于0.04°。 根据图8、9中半满载的试验结果,调转50°的时间在1.4 s左右,最大动态跟踪误差不大于0.05°。 根据图10、11中空载下的试验结果,调转50°的时间在1.4 s左右,最大动态跟踪误差值在0.04°左右。 从试验结果看出,在3种状态下系统运行平稳,动态跟踪误差最大值在0.05°左右,远高于系统0.5°的指标要求;调转50°的最长时间是1.4 s,满足系统不大于2 s的指标要求。试验结果表明该自校正PID控制器满足系统的要求。 笔者对自校正PID控制器从原理、设计方法上进行了详细的说明,并将应用于某装置的随动系统中,对该系统进行了控制器的设计,利用零-极点对消的原理计算了3种工况下的PID控制参数的设计,通过满载、半满载和空载工况试验,表明采用该控制算法,系统在稳定性和快速性方面都取得良好的控制效果,适用于变质量变负载装置的随动控制系统。3.3 随动系统自校正PID控制器设计思路
3.4 随动系统自校正PID控制器设计实现
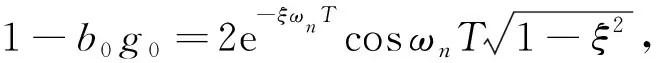
4 大角度调转控制

5 试验调试






6 结束语
