三自由度并联包装机构静动态特性建模与分析

董 旭 高铁红

(1. 北华航天工业学院机电工程学院，河北 廊坊 065000；2. 河北工业大学机械工程学院，天津 300130)

并联机构由于具有结构刚度大、运动精度高、控制相对容易、结构较为紧凑、运动惯性小等特点，被广泛应用于食品工业目标抓取、分拣、包装等方面。随着食品包装技术的发展，对并联包装机构的设计和应用逐渐提出了更高的要求，因此在设计阶段进行机构性能仿真分析具有重要的实际应用价值[1]。并联机构性能的研究主要体现在静刚度、低阶模态特性、动力学[2]等方面，集中应用了解析计算、软件仿真、工程试验等方法[3-8]。耿明超等[9]基于虚功原理分析了4UPS/UPR并联机构刚度；付红栓等[10]应用Lagrange方程建立了三自由度并联机构动力学模型，依托仿真软件求得了机构驱动环节的驱动力。钱太利等[11]依据并联机构杆件受力方式确定了应力最大位置，并研究了一类典型并联机构柔性杆件动态特性。张洪等[12]在柔顺变形情况下建立了3T并联机构弹性动力学方程并进行了仿真。吴超宇等[13]利用虚功原理建立了直线驱动型并联机器人反向动力学模型，并分析了各运动部件的广义力及其影响因素。Geethapriyan等[14]、Cretescu等[15]、Lu等[16]对三自由度并联机构进行了静力学、运动学、动力学建模与仿真。上述研究主要应用了Lagrange法、牛顿—欧拉法、凯恩法、虚功原理等理论建模方法与软件仿真方法研究机构性能，且大部分是将构件按照纯刚体对待，较少考虑构件的弹性变形与刚柔耦合因素。文章拟针对3-HUU型并联机构，在确定其静刚度以及低阶模态特性基础上，建立机构刚柔耦合动力学模型。通过对各个模型设置具体边界条件并进行仿真，得到具体静动态特性数据，旨在为机构后续优化以及应用提供依据。

1 并联包装机构构型

三自由度并联机构几何模型如图1所示。HUU构型中，H代表螺旋副，U代表万向铰。整个机构主要由3个滚珠丝杠、3个滑鞍、3组支链共6个连接杆、静平台、动平台组成。每个支链中，万向铰链两端分别连接滑鞍和动平台，电机通过联轴器与丝杠连接。滚珠丝杠转动带动滑鞍滑动使得动平台沿空间笛卡尔坐标系3个方向直线运动，从而构建三自由度平动机构运动体系。该机构末端动平台若配备包装机械手，辅助于控制系统，即可满足食品包装需要[17]。并联机构简图如图2所示，空间均布3组共6支连接杆件，其中11杆与12杆为第1组支链，21杆与22杆为第2组支链，31杆与32杆为第3组支链。各支链协调运动实现动平台沿空间3个方向运动。

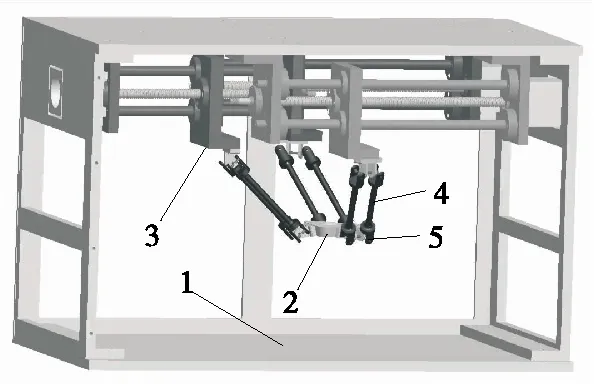
1. 静平台 2. 动平台 3. 滑鞍 4. 支链 5. 万向铰

图2 并联机构简图

2 并联机构刚度有限元分析

2.1 有限元分析设置

三维模型依托软件创建，在对模型进行适当简化调整后导入有限元软件中。在保证模型分析计算精度和结果的准确性前提下调整不受力或者受力很小的零部件特征。设置材料属性参数：弹性模量2.06E11 Pa，泊松比0.29，密度7 850 kg/m3。划分网格后共获得217 687个节点，110 903个单元。

2.2 静刚度计算

设置模型底面为固定约束，分别在动平台中心(566.55，247.24，-260.00)位置施加沿基础坐标系X、Y、Z方向作用力，大小为300 N，3种情况整机位移图如图3～图5所示，静刚度计算结果如表1所示。

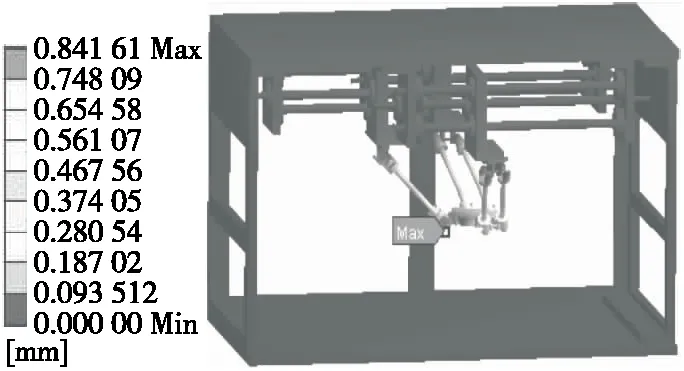
图3 X方向受力位移图

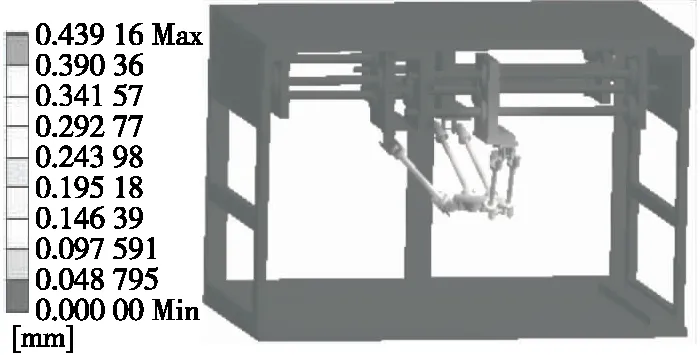
图4 Y方向受力位移图

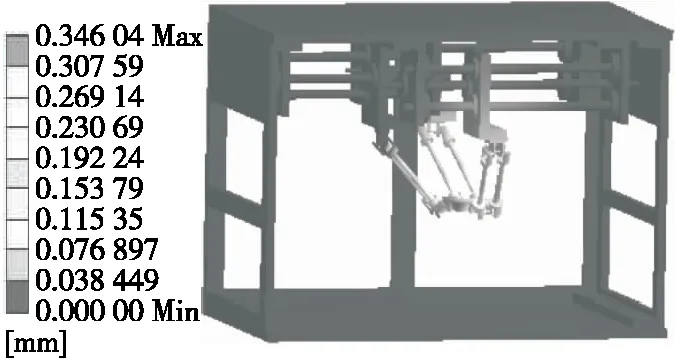
图5 Z方向受力位移图

表1 静刚度计算结果

由表1可知，机构沿Z方向刚度性能最好，X、Y方向静刚度值偏低，优化结构时应重点考虑。当机构动平台沿X、Y方向受力时，最大应力位于31号杆件与动平台连接的铰链位置；当机构动平台沿Z方向受力时，最大应力位于21号杆件与动平台连接的铰链位置，说明万向铰链处为结构薄弱环节。

2.3 机构动刚度分析

依托有限元软件中模态分析模块对机构支链环节进行模态分析，前期设置与静刚度分析完全一致，限制滑鞍沿Y、Z方向的自由度，静平台设置为全部约束，前10阶模态计算结果如表2所示，部分阶次相对位移如图6～图8所示，机构相对振动位移较大环节在第1、3支链。综合各阶次的分析结果，连接杆件与动平台和滑鞍连接处振动位移较大。

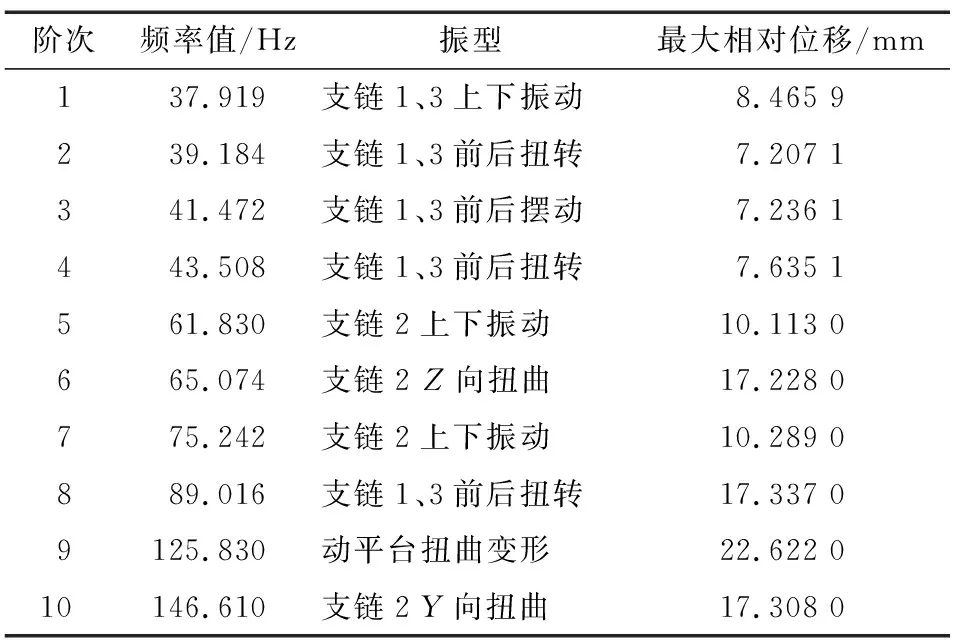
表2 模态分析结果

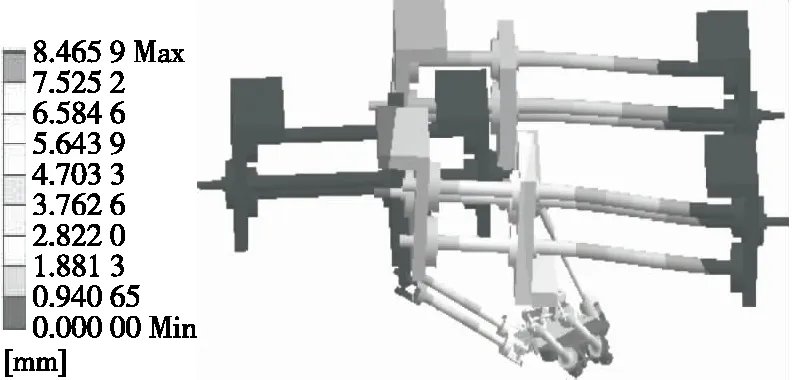
图6 第1阶振型

图7 第2阶振型

图8 第6阶振型

3 机构动力学建模

基于并联机构的结构系统的复杂特点，应用Lagrange法建立并联机构动力学模型[18]。3-HUU并联机构系统Lagrange动力学方程为[19]：

(1)

式中：

L——Lagrange函数；

T——机构总动能，J；

V——机构总势能，J；

qk——系统广义坐标；

Qk——作用在系统上对应于广义坐标的外力，N。

所以并联机构移动副轴向驱动力：

(2)

并联机构运动平台速度是X、Y、Z 3个方向分速度的合成，取3个方向速度分别为VX、VY、VZ。定义动平台质量为m，3组支链6个连接杆件质量分别为m11、m12、m21、m22、m31、m32，3个滑鞍质量相同为ml，选取动平台质心点坐标为广义坐标，则q=[X0,Y0,Z0]T，广义力为Q=[Q1,Q2,Q3]T，取M1=m11+m12，M2=m21+m22，M3=m31+m32。

3.1 并联机构总动能计算

动平台受3个方向分速度影响，动平台动能为：

(3)

式中：

连接杆受到X方向分速度影响，产生动能为：

(4)

连接杆11的动能为：

(5)

Y方向分速度对连接杆的影响：

(6)

Z方向分速度对连接杆的影响：

(7)

同理可得，其余杆件受到Y、Z方向分速度影响的动能，所以6个连接杆总动能：

(8)

滑鞍动能为:

(9)

系统总动能为：

(10)

3.2 并联机构部件势能计算

取静平台底部的平面为零势能面，动平台质心在固定坐标系中Z轴方向坐标为Zc，6个连接杆的坐标分别为Z1，Z2，Z3。则动平台势能为：

V1=mgZc。

(11)

6个连接杆的势能为：

V2=M1gZ1+M2gZ2+M3gZ3。

(12)

并联机构总势能：

V=V1+V2=mgZc+M1gZ1+M2gZ2+M3gZ3。

(13)

3.3 动力学方程

根据上述推导，可得

(14)

(15)

(16)

建立机构动力学方程：

(17)

4 刚柔耦合动力学分析

4.1 动力学仿真

依托软件建立机构三维模型(见图9)，在保留机构构件基本运动关系前提下对模型进行简化处理，最终保留动平台、滑鞍、丝杠、支链等系统关键元素。将模型导入动力学软件后设置构件材料属性并添加构件之间的运动副：丝杠端部固定副、滑鞍位置的滑移副、万向铰位置的万向副。

图9 并联机构仿真模型

仿真模型驱动设置：支链1滑移副速度随时间变化函数为sin(60×time)，支链 2 驱动函数为 -sin(60×time)，支链 3 驱动函数为 -sin(60×time)。在动平台直线点施加沿-Y方向大小为50 N的力。仿真时间为10 s，总步数为100步。将机构各零部件作为纯刚体进行分析。综合静刚度分析结果与模态振型可知，支链结构承受着较大的载荷，其弹性变形和振动对机构性能产生一定的影响，因此将连接杆件转换为柔性体进行分析。具体步骤为：将每组支链分支杆件三维模型逐个保存为Parasolid格式导入有限元软件中；设置杆件的材料属性，确定实体单元类型为Solid45、Mass21，其值确定为1E-5；对连接杆进行网格划分，创建杆件外连接点，外连点坐标为(0.513 88，0.390 26，-0.467 95)、(0.570 46，0.249 14，-0.338 01)、(0.355 04，0.389 96，-0.232 57)、(0.497 05，0.249 13，-0.233 53)、(0.605 59，0.389 96，-0.074 38)、(0.627 18，0.249 14，-0.214 74)；依据连接点创建局部刚性连接区域；依次将连接杆模态中性文件导入软件中，替换原刚性构件。刚柔耦合分析设置与刚体分析完全相同。动平台质心运动位移、速度变化曲线如图10、图11所示；第3组支链中32杆所连滑鞍加速度变化曲线如图12所示，22号连接杆所连滑鞍沿X方向位移、速度、加速度变化曲线如图13～图15所示；第2组支链Joint10沿X方向驱动力与驱动矩变化曲线如图16、图17所示。

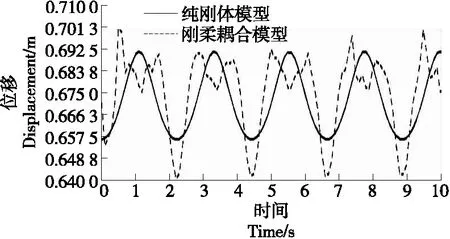
图10 动平台质心位移

4.2 仿真结果分析

通过比较刚体模型与耦合模型的位移变化曲线，刚体系统与耦合系统下的运动平台位置和姿态在10 s内基本相同，最大差值为初始时刻3 mm处，前1 s内初始运动时，动平台由静止状态到运动状态，连接杆件存在一定的弹性振动情况，振动变形影响了动平台的运动。动平台在短期震荡后，后期趋于平缓且呈规律性变化。其余时间最大差值约为2 mm，分别在1.2，3.3，5.5，7.7 s时。由图10、图11可知，耦合模型动平台速度整体高于刚体模型速度。由图12可知，第5.0 s和第6.5 s刚体模型加速度出现了突变，其余时刻两类模型分析结果基本一致。

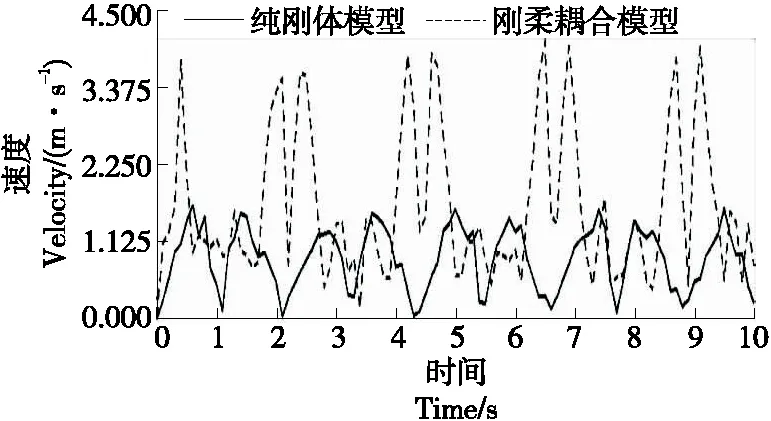
图11 动平台质心速度

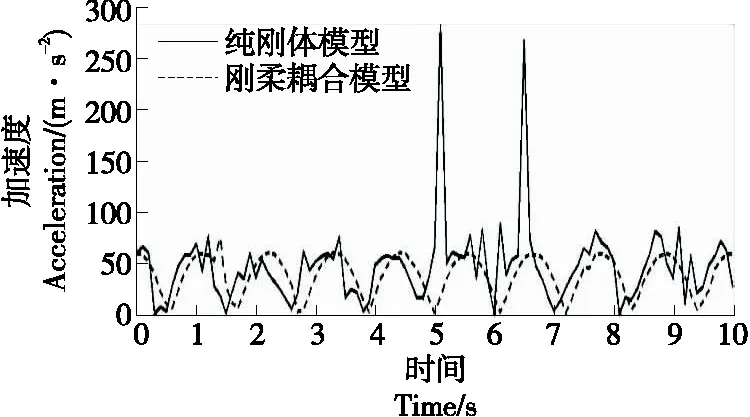
图12 32号杆连接滑鞍加速度

图13 22号杆连接滑鞍X方向位移

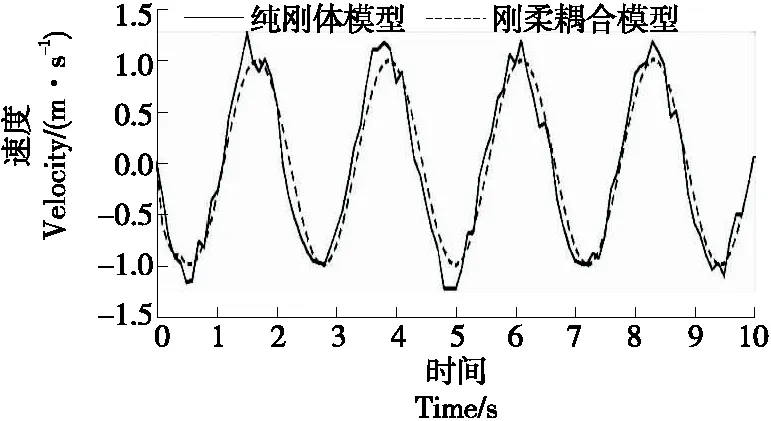
图14 22号杆连接滑鞍X方向速度

图15 22号杆连接滑鞍X方向加速度

图16 Joint 10 X方向驱动力

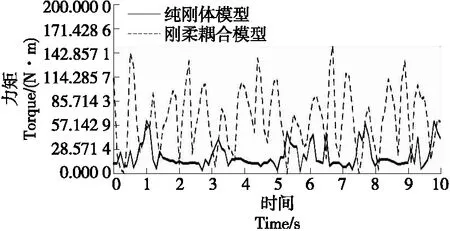
图17 Joint 10驱动力矩

由图13～图15可知，滑鞍在两类系统下的位移、速度变化趋势一致，数据基本相同。只是在加速度变化曲线中，第5.0 s和第6.5 s运动平台处于最高位置和最低位置，滑鞍在刚体系统中的加速度存在突变，与耦合系统数据存在最大偏差。

由图16～图17可知，初始时刻，耦合模型驱动力大于刚体模型起始阶段驱动力，后期时间段耦合模型驱动力基本大于刚体模型驱动力。比较此运动副输出力矩情况曲线，耦合模型运动副驱动力矩明显大于刚体模型。所以连接杆的柔体弹性变形对驱动力产生了很大影响，在结构优化时应注意提高此处动力学性能。

5 结论

以一种3-HUU型可用于食品包装行业的并联机构为研究对象，对机构进行了静动态特性建模与分析。结果表明：利用有限元分析技术计算并联机构沿空间各方向的静刚度可知，机构沿空间垂直方向静刚度最高，其余方向静刚度偏低。机构支链的低阶固有频率偏低，万向铰链两端位置是设计中的薄弱环节。机构动力学理论建模以及刚柔耦合动力学分析表明，连接杆件的刚柔耦合效应对滑鞍运动方向发生改变瞬间影响最大，出现了突变情况，两类模型其余运动性能参数变化趋势基本一致。后续在进一步优化机构时应重点考虑连接杆件的结构参数。