数形结合思想方法在高中数学教学与解题中的应用

何宗建

摘要：高中階段的学生已经有了一定的解题思维和解题方法，掌握了一定的技巧。众多的解题方法中，数形结合在数学学习的过程中，始终贯穿几何图形到数学函数的教学，在解题中应用十分广泛。因此，本文主要结合例题分析，从数形结合思想在高中数学教学与解题中的应用出发进行初步探讨，以求抛砖引玉。

关键词：数形结合;高中数学解题;应用策略

数学在高中阶段属于重点科目，通过数学知识可以解决生活中的很多实际问题。随着教育、科技的发展，传统的数学教学方式已经越来越难以满足当代学生要求简便、易懂、易掌握的需求。根据多年的教学实践，我认为数字与形状相结合的思维方法更容易在高中数学教学中实施。它是一种高效、简单的解题方法，更容易让学生理解和掌握。

一、以数解形，以形论数

因为“数”和“形”是一种对应，有些数量更抽象，我们很难把握，但是由于“形状”形象和直觉的优势，可以表达更具体的思考，在解决数学问题中起着决定性作用，因此我们可以找到相应的“定量”——“图形”，用几何图形来解决代数的问题。图形分析是将数量问题转化为图形问题，最后通过对图的分析和推理来解决数学问题的简便方法。

因此，对于“数”化为“形”这类问题，解决的基本思路是：根据条件中给出明确的目标要求，从已知结论的问题或条件入手，观察分析其是否为相似研究的基本公式或图表的表达式，或采用合适的图形，最后使用或构造图形属性、几何意义等已知条件，解决题目问题所需要解决的目标。

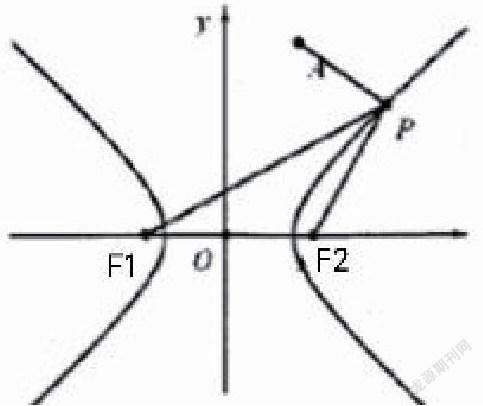
例题分析：已经F1是双曲线x2-y2/4=1的左焦点，A（1，2），P点是双曲线右支上的一个动点，那么|PF1|+|PA|的最小值是。

分析：常规的解题思路是采用解析法。将|PF1|+|PA|表示为P的坐标函数求最小值，但是这种方法的运算量较大，容易出错。因此，我们可以采用“数”转化为“形”的方法，设双曲线的右焦点为F2，利用双曲线的定义|PF1|=2a+|PF2|=2+|PF2|，所以|PF2|+|PA|最小时，|PF1|+|PA|最小，根据双曲线图形可以知道，A、P、F2三点共线时，可求出最小值。

二、以形助数，以数论形

对于比较复杂的“图形”，不仅要对数字图形进行修正，还要观察图形的特征，发现主题中隐含的条件，最大程度地利用图形或几何的意义，将自然界的“形”说成“数”的形式，加以分析计算。因此，对于“形”变成“数”这类问题，解题的基本思路是：明确给定题目中对象的条件和愿望，分析给定条件和要求对象的特征和性质，了解图形中条件或对象的几何意义，然后根据条件和结论，运用相应的公式或定理等。

例题分析：已知函数f（x）的定义域为（a，b），其导函数在其定义域内的图像如下所示，那么函数f（x）在（a，b）内有     个极小值点。

分析：找极小值点就是要找到函数由递减函数变为递增函数的点，也就是找到其导函数的值由负数到正数的点，由图可知，只有1个。

三、数形结合，互相转化

数形结合通常包括以下几部分内容：1.实数与数轴上动点的对应关系;2.定量与图形的对应关系;3.曲线与方程对应关系;4.基于几何要素和已知条件的概念，如复数运算、三角函数运算及证明等;5.所给出的方程或代数公式的结构具有明显的几何意义。

解决这类问题往往需要同时从已知和结论出发，仔细分析并找出内在的“形”与“数”的相互关系。例题分析：若0<a<π/2，求证sina<a<tana。

分析：这类证明题的一般方法是从证明不等式的传统解题方法入手，但是用这种传统的解题方法需要运用大量的公式和公式的变形。不仅计算量大，而且学生也容易出错。因此，我们利用三角函数的定义，构造出一个单位圆和一个直角三角形来组合图形。认真观察和分析构造出来的图形，可以将代数的问题几何化。

四、结语

为了提高学生数字与形状相结合的思维能力，教师需要耐心、细心地引导学生学习如何将数字与形状相结合，用思维理解数字与形状，用思维运用数字与形状，用数形结合的思维掌握定量与图形。数形结合的思想方法有利于学生深刻地理解题目含义，了解题目内在要求，教师应帮助学生形成完整的数学概念，增加学生解决问题的方法，锻炼学生的逻辑思维以及提高解题能力。

参考文献：

[1]于宏坤.浅谈数形结合思想方法在解题中的应用[J].佳木斯教育学院学报，2012（01）.

[2]钱建.例题说明数形结合思想的应用[J].中学生数学，2014（09）.

[3]杜路敏.浅析高中数学教学中数形结合思想的应用[J].学周刊，2013（22）.