大型储罐抗震设计计算在中美规范中的对比分析
2021-09-17汪蓉梅金斌戈钮建良俞新宇刘延雷
黄 泽,汪蓉梅,金斌戈,钮建良,俞新宇,刘延雷
(1.杭州市特种设备检测研究院(杭州市特种设备应急处置中心),浙江 杭州 310051;2.杭州市锅炉压力容器技术协会,浙江 杭州 310051)
大型立式圆筒形钢制储罐(以下简称大型储罐)在石油化工领域中扮演着重要角色,其安全性主要受强度、稳定性、倾覆性等因素影响【1-2】。目前,GB 50341—2014大型储罐设计标准《立式圆筒形钢制焊接油罐设计规范》(以下简称GB 50341),API 650—2013 & ADDENDUM3 2018 & ERRATA2 2014《钢制焊接石油储罐》(以下简称API 650)对抗震设计计算均有相应要求【3-4】。在地震载荷作用下,我国曾多次发生储罐破坏事故,进而导致易燃介质燃烧、有毒介质泄漏等次生灾害,既给人民群众带来生命财产的损失,也造成了严重的生态影响【5-8】。目前,大型储罐本体破坏形态为罐壁下部出现象足(轴压失稳),浮动顶与固定顶发生撞击导致罐顶附件脱落,浮顶导向管、量油管卡住导致导向管拉弯,支架变形甚至储罐整体翘离倾覆【9-13】。
本文着重比较中美设计规范中大型储罐关于抗震计算的相关规定,并结合工程实际,分析两者在罐壁纵向压缩力、抗倾覆力、晃动波高及环向应力计算等方面的差异,为完善我国大型储罐的抗震设计、促进储罐的安全运行提供借鉴和参考。
1 储罐抗震设计计算的主要参数
为保证大型储罐在地震载荷作用下的安全性,GB 50341在进行抗震设计时需计算以下参数:锚固系数、底圈罐壁最大轴向压应力、晃动波高以及导向装置最小间隙;API 650在进行抗震设计时需计算以下参数:锚固系数、底圈罐壁最大轴向压应力、晃动波高、环向应力、机械式锚固罐的倾覆稳定比以及自锚固罐的滑动阻力。下面着重讨论中美规范抗震设计时均要求计算的三个参数:锚固系数、底圈罐壁最大轴向压应力和晃动波高。
1.1 GB 50341计算的主要参数
1.1.1 锚固系数
锚固系数主要用于判定大型储罐在地震载荷作用下能否自锚固。当锚固系数值>1.54时,储罐需要进行锚固。锚固系数计算式如下【4】:
(1)
式中:J——锚固系数;
μ——弯矩调整系数,按GB 50341第D.4.2条的规定选取;
M1——总水平地震作用在储罐底部所产生的地震弯矩,MN·m;
Di——储罐内径,m;
Fw——罐壁罐顶自重通过罐壁作用在罐底单位长度上的提离反抗力,MN/m;
FL——储液提供的罐底与罐壁接触处单位长度上的提离反抗力,MN/m。
罐壁罐顶自重通过罐壁作用在罐底单位长度上的提离反抗力计算式如下:
Fw=N1/(πDi)
(2)
式中:N1——罐壁与罐顶总重量,MN;
注:为方便比较中美规范差异,对中美规范中符号相同但含义不同的情况,本文采用不同下标加以区分。GB 50341中储罐内径和API 650中储罐公称直径均采用符号D表示,本文为将二者区分开,采用Di表示储罐内径,采用D表示储罐公称直径。
1.1.2 底圈罐壁最大轴向压应力
为避免在地震条件下大型储罐罐壁下部出现象足,罐壁轴向压应力不应大于许用临界压应力【14】,由GB 50341 中第D.5.2条可知,底圈罐壁轴向压应力计算式可统一为:
σ1=CvN1/A+CLM1/Z1
(3)
式中:σ1——底圈罐壁最大轴向压应力,MPa;
Cv——竖向地震影响系数(7度及8度地震区取1.0,9度地震区取1.45);
A——按底圈壁板有效厚度计算的罐壁截面面积,m2;
Z1——按底圈壁板有效厚度计算的断面系数,m3;
CL——翘离影响系数,当0.785 按底圈壁板有效厚度计算的断面系数计算式为: (4) 式中:ti——底圈罐壁有效厚度,m。 注:GB 50341附录D中底圈罐壁有效厚度和API 650附录E中底圈罐壁名义厚度均采用符号t表示,本文为将二者区分开,采用ti表示底圈罐壁有效厚度,采用t表示底圈罐壁名义厚度。 底圈罐壁许用临界应力按式(5)计算: [σcr]=0.22Eti/Di (5) 式中:[σcr]——罐壁许用临界应力,MPa; E——设计温度下底圈罐壁材料的弹性模量,MPa。 1.1.3 晃动波高 在地震载荷作用下,储罐内液体晃动撞击到罐顶可能会导致罐顶附件脱落,因此,储罐内液面到罐壁顶部的距离应大于罐内液面晃动波高【15-16】。在水平地震作用下,罐内液面晃动波高的计算式为: (6) 式中:hv——液面晃动波高,m; α——地震影响系数,根据液体晃动基本周期及地震影响系数最大值确定; R——储罐内半径,m。 1.2.1 锚固系数 API 650也通过锚固系数来判定大型储罐在地震载荷作用下能否自锚固。当锚固系数数值>1.54时,储罐可通过机械锚固的方法来保证其稳定性。锚固系数计算式如下【13】: (7) 式中:Mrw——环墙弯矩,作用在该罐壁基础的周边的部分倾覆力矩,MN·m; D——储罐公称直径,m; Av——竖向地震加速度系数,%g; Fp——操作压力与设计压力比值,且不低于0.4; wint——单位圆周长度上的介质压力引起的设计计算拔锚载荷,MN/m。 注:为方便比较中美规范差异,本文对同一变量采用相同的符号。本文采用Fw(API 650标准采用wt符号)表示罐壁罐顶自重(包括罐顶其他载荷)通过罐壁作用在罐底单位长度上的提离反抗力,采用FL(API 650标准采用wa符号)表示储液提供的罐底与罐壁接触处单位长度上的提离反抗力。 1.2.2 底圈罐壁最大轴向压应力 为避免在地震条件下大型储罐罐壁下部出现象足,罐壁轴向压应力不应大于许用临界压应力,由API 650 附录E.6.2.2可知,当J≤0.785或J>1.54时,底圈罐壁轴向压应力计算式为: σ1=[Fw(1+0.4Av)+1.273Mrw/D2]/ti (8) 当0.785 (9) 注:为方便比较中美规范差异,本文对同一变量采用相同的符号。本文采用σ1(API 650标准采用σc符号)表示底圈罐壁最大轴向压应力,采用ti(API 650标准采用ts符号,单位为mm)表示底圈罐壁有效厚度。 底圈罐壁许用临界应力按式(10)计算: (10) 式中:G——相对设计密度; H——最高设计液位,m; Fty——底圈壁板最低屈服强度,MPa; k——系数。 k=GHD2/t2 式中:t——底圈壁板公称厚度,mm。 1.2.3 晃动波高 在水平地震作用下,罐内液面晃动波高的计算式为【3】: hv=0.42DAf (11) 式中:Af——晃动波高计算时的加速度系数,%g。 大型储罐径厚比通常在1 000以上【17】,储罐公称直径、储罐内径、储罐外径差别很小,对计算结果基本无影响,为方便对比,统一采用储罐公称直径D进行分析。API 650通过垂直地震加速度体现竖向地震的影响,并认为当考虑垂直地震加速度时,在计算抵抗基础上的最大上拔力时,应考虑系数1-0.4Av,当计算承压向下载荷时,应考虑系数1+0.4Av,而GB 50341则通过Cv来体现竖向地震影响因素对承压向下载荷的影响。 API 650—2007(API 650—2007 12th ed.)中认为,锚固系数计算式为【18】: (12) 根据API 650—2007,垂直地震加速度计算式为: Av=0.14SDS (13) 式中:SDS——5%阻尼设计,以ASCE 7的方法为基础的短时间(0.2 s)内反应谱相应加速度,%g。 由于0.4Av=0.056SDS≪1【4】,因此,式(12)可变为: J=Mrw/[D2(Fw+FL)] (14) 根据GB 50341条文说明中附录D.4可知,Mrw=μM1,则式(14)和式(1)表达式一致,即GB 50341中锚固系数计算式是根据API 650—2007中的公式推导而来,且根据相同的锚固系数判定准则来判定储罐是否需要设置地脚螺栓。但API 650考虑了罐壁内部工作压力对锚固系数的影响,且认为垂直地震加速度Av=0.47SDS而非原先的Av=0.14SDS,此时简单地忽略垂直地震加速度的影响对锚固系数的计算会造成较大误差,因此,这导致对同一工况的储罐分别采用中美规范进行抗震设计时,计算出的锚固系数值差异较大。 此外,由GB 50341附录D.4.2的条文说明可知,GB 50341表D.4.2-1中弯矩调整系数只是针对于API 650中D类场地类别、储罐重要度系数为1的情况进行的计算转化,而根据API 650附录E.6.1.5和E.4.6.1中的计算方法,不同的场地类别和不同的储罐重要度对环墙弯矩Mrw的计算结果有影响,因此,GB 50341附录D中转化而来的弯矩调整系数有一定的局限性。这进一步加剧了对同一工况的储罐分别采用中美规范进行抗震设计时,其锚固系数差异较大的情况,具体可见文中实例。建议GB 50341标准修订时,考虑不同场地类别和不同储罐重要度对弯矩调整系数的影响。 由此可见,中美规范进行抗震计算时,锚固系数值的差异主要由于API 650中考虑了竖向地震加速度和罐壁内部工作压力对锚固系数的影响,而GB 50341均未考虑这两者带来的影响;此外GB 50341中的弯矩调整系数只针对API 650中的D类场地类别、储罐重要度系数为1的情况,当储罐在其他场地类别以及储罐重要度发生变化时,也会导致锚固系数计算结果的差异。 本节为方便讨论,仅讨论垂直地震加速度Av=0(即不计入垂直地震力)、Cv=1的情况。由1.1.2 节和1.2.2节可知,底圈轴向压应力受锚固系数数值的影响。当J≤0.785或J>1.54时,由式(2)、式(3)和式(4)可知: σ1=[Fw+1.273M1/D2]/ti (15) 同理,式(8)变为: σ1=[Fw+1.273Mrw/D2]/ti (16) 比较式(15)和式(16)可见,两者表达形式一致,但GB 50341在计算底圈轴向最大压应力时,未如锚固系数计算公式一样引入弯矩系数,导致在J≤0.785或J>1.54时,中美规范计算有差异。 当J=0.785+Δ(Δ=1/+∞)时,底圈轴向压应力采用式(9)计算。联立式(9)和式(12)可知: σ1=[Fw+1.273Mrw/D2]/ti (17) 由于Δ>0,但无限接近于0,由式(16)和式(17)可知,当锚固系数J=0.785+Δ时,API 650—2007中底圈最大轴向压应力的计算结果和锚固系数J=0.785时一致,即可认为式(8)和式(9)在锚固系数为0.785时取值连续。 当J=1.54时,同一储罐是否增加地脚螺栓对Mrw取值影响不大。联立式(9)和式(12)可知: σ1=[Fw+4.44×1.273Mrw/D2]/ti (18) 由式(16)、式(17)和式(18)可知:当锚固系数接近0.785时,其翘离系数约等于1,小于GB 50341中的1.4;当锚固系数接近1.54时,其翘离系数约等于4.44,大于GB 50341中的1.4。因此当0.785 上述推导是基于API 650—2007中锚固系数的计算公式,API 650和API 650—2007相比较,锚固系数的计算公式发生了变化,但底圈最大轴向压应力计算公式不变。因此必然出现当锚固系数为0.785时,分别采用式(8)和式(9)计算,底圈最大轴向压应力求值发生跳跃的现象,不甚合理,建议考虑罐壁内部工作压力对底圈最大轴向压应力的影响。 令C=FL-Fpwint,比较式(7)和式(12)可知,新版API 650相当于用C取代了API 650—2007中的FL,因此式(9)中的FL由C取代,可保证底圈最大轴向压应力的变化是连续的,因此,式(9)可修正为: (19) 因此,当J≤0.785或J>1.54时,中美规范的形式是统一的,两者的计算结果差异主要是由于API 650考虑的竖向地震载荷影响因子是1+Av,而GB 50341考虑的竖向地震载荷影响因子是Cv,两者取值的差异以及Mrw和M1之间未考虑弯矩调整系数的影响导致了其计算结果的差异;而当0.785 中美规范中,晃动波高均与储罐的直径成正比,GB 50341主要由地震影响因素以及储罐罐形决定,而API 650根据储罐组别SUG、储罐晃动基本周期以及调整阻尼反应谱系数和反应谱响应加速度参数共同决定。 某固定顶储罐,材质为碳钢,设计压力为0 kPa,设计温度下材料弹性模量为201 000 MPa;直径15 m,储罐设计液位10 m,罐壁总高10.8 m,储液相对比重1.0,底圈壁板及底板边缘板有效厚度均为8.2 mm;底圈壁板及底板边缘板材质的屈服强度为345 MPa,设计基本地震加速度0.2g,储罐罐壁及其附件的质量为46 052 kg,罐顶及其附件的质量为19 812 kg,罐底质量10 898 kg。下面分别计算场地类别为A、D、E时储罐的锚固系数及底圈壁板轴向压应力,计算结果见表1。 表1 中美规范锚固系数及底圈壁板轴向压应力计算结果 GB 50341场地类别的划分和API 650不一样,本案例中没有给出中美规范中不同场地类别之间相互的对应关系,但由GB 50341第D.3.7条可知,对最大储存量小于10 000 m3的储罐,地震影响系数的取值与场地类别无关,因此本案例中无需转化中美规范中场地类别的关系也可比较抗震的主要计算参数。对需转换中美规范中场地类别的情况,可参考文献【19】中的做法。 由表1可知:对同一操作工况下的储罐,按GB 50341中的公式计算,在不同的场地类别下,罐壁底部水平剪切力、罐壁底部倾覆弯矩、罐壁最大轴向压应力、锚固系数计算值不变;而按API 650中的公式计算,上述参数随着场地类别的变化而有所不同。 在场地类别D的设计条件下,GB 50341和API 650计算的结果差异最小,其中罐壁底部倾覆弯矩、罐壁最大轴向压应力的差比均在5%之内;而锚固系数的差异主要是由于API 650中考虑了垂直地震加速度的影响,而GB 50341在计算锚固系数时未考虑该因素。当场地类别不为D时,GB 50341和API 650的计算结果差异很大,其中罐壁最大轴向压应力的差比有超过100%的现象,这主要是由于GB 50341中的翘离系数为定值,而API 650中的翘离系数和锚固系数密切相关。 针对本案例,若将储液相对比重改为1.1、场地类别改为E,其他条件不变,则按GB 50341计算,锚固系数为0.972,按API 650计算按为1.563,从而出现按GB 50341设计该罐为自锚固罐,而按API 650设计为机械式锚固罐的情况。这主要是由于GB 50341在确定锚固系数时,虽然采用了API 650—2007中附录E的规定,但未考虑场地类别、垂直地震加速度等因素的影响,导致对同一工况下的储罐进行设计时,两者在区分储罐是否为锚固罐时差异较大。 基于上述分析可得出如下结论: 1)API 650和GB 50341均通过锚固系数来判定储罐是否自锚固,两者的表达式基本一致,但GB 50341未考虑内压、竖向地震加速度对锚固系数的影响,弯矩调整系数只是针对于API 650中的D类场地类别和储罐重要度系数为1的情况,未考虑不同场地类别和不同储罐重要度的影响,因此,有时两个规范锚固系数的计算结果差异较大。 2)当J≤0.785或J>1.54时,中美规范中底圈轴向压应力计算公式中的形式是统一的,两者计算结果的差异主要是由竖向地震加速度取值的差异,以及Mrw和M1之间未考虑弯矩调整系数的综合影响导致的;而当0.785 3)对晃动波高,GB 50341主要考虑了罐形的影响,API 650则考虑了地震用途组别、储液晃动基本周期、反应谱加速度等多种因素的影响。
1.2 API 650计算的主要参数
2 分析讨论
2.1 中美规范锚固系数的差异
2.2 中美规范底圈轴向压应力的差异
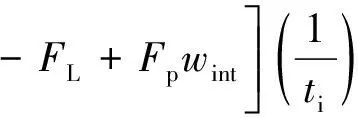
2.3 中美规范晃动波高的差异
3 计算实例

4 结语
