p-型层状氧化锌的热电性质研究

李思桦， 李永华， 吕 兵， 王晓璐

(1. 贵州师范大学 物理与电子科学学院， 贵阳 550000； 2. 贵州师范大学 基建管理处， 贵阳 550000)

1 引 言

自从石墨烯被英国曼彻斯特大学物理学家用微机械剥离法从石墨中分离出来以后，打破了大多数物理学家认为的热力学涨落不允许二维晶体存在于有限温度的看法[1-6]. 由于石墨烯在光学、电学、力学等方面表现出的优异特性，引起了大家对于二维材料的广泛关注. 一方面，氧化锌(ZnO)是一种具有宽带隙(3.37 eV)[7]的半导体，其有优异的电荷载流子输运性能、在高温下的强稳定性、制作原材料价格低廉和制作方法简便受到了大家的日益青睐. 已有研究表明，当纤锌矿结构氧化锌的体积减少到几个原子层时，氧化锌可以转化为和石墨烯一样平面且呈蜂窝状结构，氧化锌之间的化学键由sp3杂化转为sp2杂化[8].

另一方面，环境污染和能源枯竭随着工业化的发展变得日益严重，而电能作为人类生活所必须的能源，使得热电材料作为一种清洁能源走入了人们的视野[9, 10]. 热电材料的理论基础是塞贝克效应和珀尔帖效应，说明了热能和电能可以直接转换. 对于材料的热电性质的热电性能可以用无量纲的热电优值ZT值来衡量,其中

公式中的S为塞贝克系数，σ为电导率，T为温度，κι为晶格热导率和κe为电子热导率. 从公式中可以看出当S2σ越大，而κι+κe越小时，则一个材料的热电性能越优越，人们通常将S2σ称为功率因子[9]. 因此，在寻找高效的热电材料时，通常是寻找低热导率材料或者有更高塞贝克系数的材料. 二维氧化锌比起其三维结构有着更小的带隙，并且已有文章报导了二维氧化锌具有较小的晶格热导率[11]，理论上讲二维结构的材料随着其层数的增加其晶格热导率会降低[12, 13]，所以它的二层结构可能会有更好的热电性能，本文通过计算得到了热力学性质更加稳定的二维氧化锌一层结构并以此构建二层氧化锌，进而研究了二层氧化锌的热电性质，希望可以为实验和实际应用提供理论参考.

2 理论及计算方法

为了研究二层二维氧化锌的热电性质，本文基于密度泛函理论使用维也纳从头计算软件包(VASP)[14, 15]进行结构优化，并选择广义梯度近似(GGA)下的Perdew- Burke- Ernzerhof(PBE)泛函作为交换关联泛函[16]. 在优化前经过收敛性测试，平面波截断能使用600 eV，第一布里渊区积分k点使用13×13×2 Monkhorst-Pack 网格. 由于二层氧化锌层与层之间的相互作用力不可以忽视，所以在优化时使用DFT-D3方法进行范德华修正[17, 18]，确保优化后的电子弛豫能量收敛标准为10-8eV. 同时为了消除周期性层与层之间的相互影响，我们在Z轴方向添加25 Å厚度的真空层.

我们使用ShengBTE软件包[19]，通过计算得到材料的晶格热导率，其原理是基于玻尔兹曼输运方程完全迭代，在输入通过PHONOPY软件计算得到的二阶力常数，和使用空间有限差分位移法计算得到的三阶力常数可以得到材料的晶格热导率. 使用BoltzTraP软件[20]可以得到材料的电子输运性质，它的原理是使用半经典玻尔兹曼理论和对能带的光滑傅里叶实行积分，通过计算得到塞贝克系数和电导率.

3 数据及结果分析

3.1 晶格优化和声子谱

从纤锌矿结构的氧化锌得到二维单层氧化锌的模型，利用vasp对二维单层氧化锌进行优化，为了消除二维单层氧化锌层与层之间的周期性影响，在搭建晶胞结构时在Z轴方向加25 Å真空层，优化前通过测试，截断能使用600 eV，布里渊区积分k点为8×8×1的Monkhorst-Pack网络开始优化，得到优化后的晶胞结构，单层氧化锌的键长b=1.899 Å以及晶格常数a=3.289 Å，与理论值b=1.851 Å和a=3.206 Å[21]比较吻合，表明优化后的结构是可信的. 如图1(a)和图1(b)所示，表现了单层氧化锌的俯视图和侧视图，可以看出单层氧化锌不是纯平面而是带有轻微的褶皱；图1(c)展示了没有虚频的单层氧化锌声子谱，因为声子谱没有虚频，展现分子的热力学稳定性，所以说本次优化得到的晶胞结构热力学是稳定的并且比起文献[21]文中的单层氧化锌结构更加稳定. 通过使用优化后的单层氧化锌考虑层间范德华力之后进行累加，通过优化得到二层氧化锌，其键长b=1.936 Å和晶格常数a=3.352 Å，可以看出单层氧化锌增加层厚后键长和晶格常数都会增大. 图2(a)和图2(b)则展示了二层氧化锌的晶胞结构图和侧视图，二层氧化锌的从图2(a)可以看出层与层之间锌原子和氧原子是交替出现的，而不是层与层之间各个原子相对应的出现，从结构的稳定性上讲是合理的；并且从图2(c)展示的声子谱没有虚频，则表明了优化后得到的二层氧化锌热力学是稳定的.

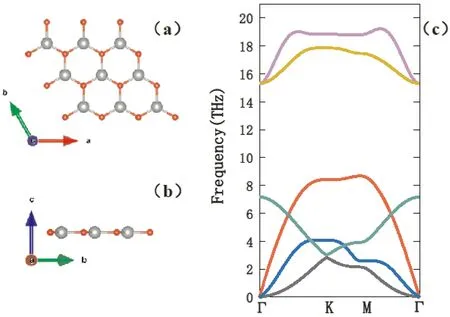
图1 (a)单层氧化锌的俯视图，(b)单层氧化锌侧视图，(c)单层氧化锌的声子谱Fig. 1 (a) Top view of monolayer zinc oxide, (b) the side view of monolayer zinc oxide, and (c) phonon spectrum of monolayer zinc oxide.

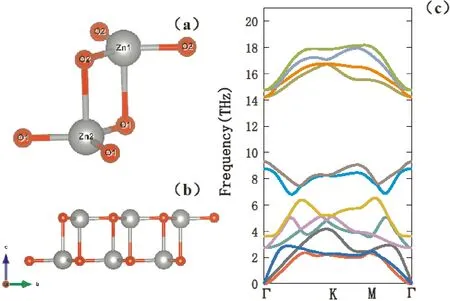
图2 (a)二层氧化锌的分子结构, (b)二层氧化锌的侧视图, (c)二层氧化锌的声子谱Fig. 2 (a) Molecular structure of two-layer zinc oxide, (b) the side view of two-layer zinc oxide, and (c) phonon spectrum of two-layer zinc oxide

3.2 热输运

材料的热输运性质对于器件在热电性能上的效率和应用是非常重要的，而声子在半导体中控制着热输运，图3表示了二层氧化锌的声子散射，图中红色圆圈，蓝色三角和紫色菱形代表声学支，棕色五星是光学支，从声子散射图中可以看出光学支有间隙，这个与声子谱中的间隙是对应的，并且从图中可以看出声学支的散射率总体上是低于光学支的散射率.

图3 二层氧化锌的声子散射Fig. 3 Phonon Scattering of two-layer zinc oxide.

目前对于声子热导率大家普遍使用的方法是求解玻尔兹曼输运方程(BTE)，而最近也有松弛时间近似(RTA)的方法被应用[22, 23]. 至今为止已有实验室研究了单层氧化锌的热输运性质，在室温下其晶格热导率为κι=4.5 W/m·K[11]，本文在BTE和RTA方法下计算了二层氧化锌的晶格热导率，图3展示了在30 K至1200 K温度下二层氧化锌的晶格热导率，在室温下分别为κιBTE=2.65 W/m·K和κιRTA=2.38 W/m·K,从对已有的二维材料在不同层厚下的热输运的研究可以得到当二维材料的层厚增加时晶格热导率是不断减少的，所以本文得到的二层二维氧化锌的晶格热导率是合理的.

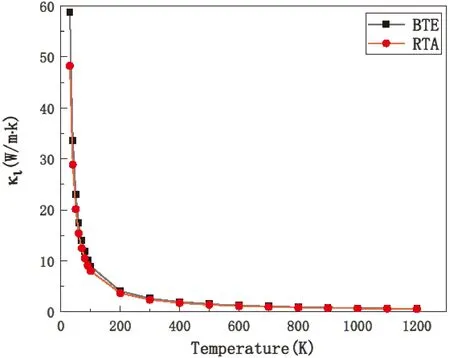
图4 使用BTE和RTA方法计算得到的30 K至1200 K温度下二层氧化锌的晶格热导率Fig. 4 The lattice thermal conductivity of two- layer zinc oxide at temperatures from 30 K to 1200 K was calculated using BTE and RTA methods.

3.3 电子输运

使用玻尔兹曼理论可以对电子输运的重要系数Seebeck系数(S)、电导率(σ)和电子热导率(κe)进行计算，因为载流子浓度对于S,σ和κe有很大的影响，所以计算时我们选择rigid-band近似模拟掺杂. 我们通常会把S2σ称为功率因子(Power Factor-PF)，以热电优值ZT来判断材料热电性能的好坏，从公式中可以看出Seebeck系数对于材料的功率因子和热电优值是至关重要的. 因为对本征半导体来说，电子和空穴浓度基本上相同，所以本文将只对二层氧化锌的p型掺杂进行报道.

图5给出了二层氧化锌的Seebeck系数在300 K、600 K和900 K等差温度下随载流子浓度变化的曲线，从图中可以看出Seebeck系数随着温度的升高而增大，这与其它材料不论是在实验结果还是理论计算得到的Seebeck系数与随着温度的变化得到的关系是一致的，表明在合理的载流子浓度下，高温下产生的Seebeck系数会较高. 材料产生的有用的电功率是由它的功率因子PF=S2σ来量化的，图6显示了二层氧化锌的功率因子在300 K、600 K和900 K温度下随载流子浓度变化的曲线，图中展示了功率因子随着温度的升高而增大，这与Seebeck系数随着温度升高而增大有关，而功率因子与载流子浓度的关系则是先随着载流子浓度的增大而增大到达峰值之后再减小，其在300 K、600 K和900 K下的功率因子最大值分别4.98×10-4W·m-1K2、1.90×10-3W·m-1K2和4.27×10-3W·m-1K2.

图5 二层氧化锌的Seebeck系数在300 K、600 K和900 K温度下随载流子浓度变化的曲线Fig. 5 Seebeck coefficient of two-layer zinc oxide varies with carrier concentration at temperatures of 300 K, 600 K and 900 K.

图6 二层氧化锌的功率因子在300 K、600 K和900 K温度下随载流子浓度变化的曲线Fig. 6 The power factor of two-layer zinc oxide varies with carrier concentration at 300 K, 600 K and 900 K

最后，我们根据计算出的热输运系数和电子输运系数来得到二层氧化锌的热电优值.ZT值大的材料为高效的热电材料，高功率因子和低导热系数是获得高ZT值的必要条件，影响功率因子的因素除了普遍认为的因材料本身性质决定的因素外，在实验上可以通过改变掺杂浓度来调整费米能级以达到最大的功率因子，而热导率则可以通过纳米结构来降低. 利用计算出的电导率、Seebeck系数和晶格热导率得出二层氧化锌的ZT值，图7展示了二层氧化锌的热电优值在300 K、600 K和900 K温度下随载流子浓度变化的曲线，在300 K、600 K和900 K下的ZT值分别为0.052、0.359和0.601，图中ZT值随载流子浓度的增加而减小，并且随着温度的升高而增大，这与温度升高功率因子增加和晶格热导率降低是符合的.

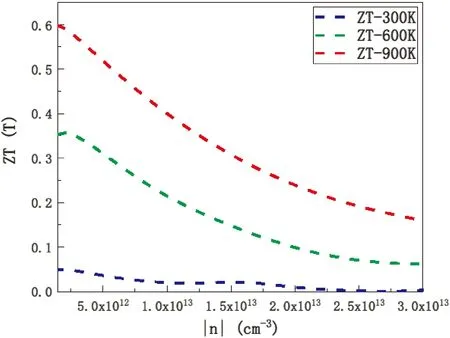
图7 二层氧化锌的热电优值在300 K、600 K和900 K温度下随载流子浓度变化的曲线Fig. 7 The thermoelectric figure of merit of two-layer zinc oxide varies with the carrier concentration at 300 K, 600 K and 900 K temperatures.

4 结 论

我们基于密度泛函理论计算了二层氧化锌的晶体结构，得到了单层和二层氧化锌的平衡晶格参数分别为a1=3.206 Å 和a2=3.352 Å，以及Zn和O它们之间的键长分别为b1=1.851 Å和b2=1.936 Å，并且单层氧化锌的并非纯平面而是有轻微的褶皱. 利用玻尔兹曼输运理论研究，得到了没有虚频的单层氧化锌声子谱，证明了用来构建二层氧化锌的单层氧化锌结构更加稳定，并得到了没有虚频的二层氧化锌声子谱，证明了二层氧化锌的热力学稳定性. 通过ShengBTE软件包和PHONOPY软件计算了二层氧化锌的二阶力常数和三阶力常数得到了二层氧化锌的声子散射率，使用BTE方法和RTA方法计算得到的在30 K至1200 K的晶格热导率，它们在室温下的晶格热导率分别为κιBTE=2.6 5W/m·K和κιRTA=2.38 W/m·K. 通过BoltzTraP软件计算了p-型二层氧化锌的电子输运，得到了其在300 K至900 K等差温度下塞贝克系数、功率因子以及热电优值，结果表明：在300 K至900 K等差温度下的热电优值为0.052～0.601. 因此，二层氧化锌在室温下的热电优值很低，但是可以随着温度的增高对热电优值进行调节，并且其在室温下的晶格热导率较低，可以在其他方面得到应用.