基于灰度重构和PSO的FCM分割MRI

周同驰，李 征，瞿博阳，李 召，宋晓炜

(中原工学院 电子信息学院，河南 郑州 450007)

0 引 言

在计算机辅助诊断中，磁共振图像(MRI)发挥了重要作用，同时，大量学者对MRI分割展开了研究。分割时，常用的方法有神经网络[1]、分水岭[2]、水平集[3]、高斯混合模型[4]、模糊C均值(FCM)[5,6]等。其中，FCM模型是一种无监督学习，允许将一个像素分为一类或多类，之后根据隶属度值进行分类，属于软分类。由于FCM模型具有理论易懂、执行简单等优点，受到了大量学者的研究，但分割结果容易受到噪声和初始聚类中心的影响。

为解决噪声敏感问题，许多学者添加滤波操作或改进FCM模型的目标函数[7]。王小鹏等[8]提出一种自适应滤波的快速广义模糊C均值算法，通过非局部像素的噪声概率自适应确定参数平衡因子，将该因子用于抑制噪声，取得了更准确的结果。其中，原始的快速广义模糊C均值算法(FGFCM)是先对像素点灰度进行线性加权和生成新的灰度图像，然后利用直方图进行分割。周友行等[9]提出了一种考虑像元间相互关系的FCM聚类分割算法，使算法具备了更好的抗噪能力。Lei等[10]提出一种基于形态重构和隶属度滤波的快速鲁棒性模糊C均值(FRFCM)聚类算法，对原图像进行形态学重构，并使用隶属度滤波，提高了隶属度矩阵的有效性。为解决初始值影响算法性能的问题，Zhang等[11]将粒子群算法与FCM模型相结合，提出了PSOFCM算法，并在实验中取得了较好的结果。胡学刚等[12]利用非局部空间信息构建和图像，根据和图像的直方图，自动选择初始化聚类中心，在分割时取得了理想的效果。冯飞等[13]使用引力搜索算法确定最优聚类中心，避免了随机初始聚类中心对分割结果的影响。为同时解决FCM模型对噪声敏感和初始聚类中心影响分割结果的问题，提出一种融合灰度重构和改进的粒子群算法的FCM模型。应用所提算法对MR图像进行分割实验，并与同类型的算法的实验结果进行对比，结果显示，所提算法具有较强鲁棒性和较高的分割精度。

1 相关算法

1.1 模糊C均值(FCM)

在FCM聚类算法中，对于给定的图像数据集X={x1,x2,…,xN}，xi为每个像素点的灰度值，其目标函数为

(1)

式中：N为图像的像素个数，c为聚类中心个数，m为模糊隶属度系数，uik为第i个像素属于第k个聚类中心的隶属度，对隶属度的约束如式(2)所示，xi和vk分别为第i个像素灰度值和第k个聚类中心灰度值，两者差的平方为其欧氏距离。在隶属度的约束下，利用拉格朗日最小二乘法分别对聚类中心和隶属度求导，可得FCM算法的聚类中心和隶属度更新公式，如式(3)和式(4)所示

(2)

(3)

(4)

1.2 快速广义模糊C均值(FGFCM)

在FGFCM聚类算法中，计算窗口内像素的灰度值和空间坐标信息进行相似度测量，并作为一个权重对灰度值进行重构，之后利用灰度级数代替像素个数进行迭代计算。因灰度级数远远小于像素个数，大大降低了计算复杂度。其目标函数为

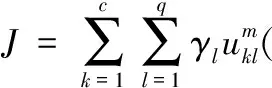
(5)

式中：q为图像的灰度级数，γl为灰度为l的像素个数，ξl是在原图像的基础上经过线性加权和生成的新图像。线性加权和的过程可表示为

(6)

(7)

Ss_lj=exp(-max(|aj-al|,|bj-bl|)/λs)

(8)

(9)

其中，Slj为像素l与像素j的相似度系数，j是窗口内除中心点外的其余像素，Nl是以像素l为中心的窗口，Ss_lj和Sg_lj分别为空间坐标信息和灰度信息，a和b分别为像素点的横坐标和纵坐标。FGFCM算法的聚类中心更新公式为

(10)

隶属度更新公式为

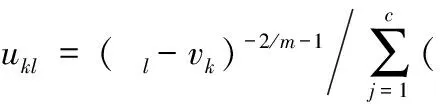
(11)

2 提出的算法

2.1 灰度重构

规则的邻域窗口通常会破坏图像的真实局部结构，导致分割结果不佳[14]；另一方面，使用图像中的每两个像素的信息可以有效地抑制噪声[15]。为更好平衡降噪与图像细节保留的关系，本文提出一种灰度重构方法。将整幅图像作为一个窗口，计算第i个像素与其余像素的灰度信息和空间坐标信息，将两者乘积作为相似度系数。再根据相似度系数对第i像素进行线性加权和，之后进行Top-hat和Bottom-hat变换完成灰度重构。其中，在计算空间信息时，使用快速带宽法自适应生成相关参数，减少参数设置问题对分割结果的影响。线性加权和图像Xi生成过程如下所示

(12)

(13)

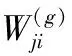
(14)

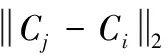
(15)

xj为第j个像素点的灰度值，H可表示为

(16)

式中：di为灰度偏差，如式(17)所示

(17)

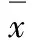
在进行灰度线性加权和后，进行Top-hat和Bottom-hat变换处理。Top-hat和Bottom-hat变换是图像差分与形态学操作相结合的结果，也是灰度图像特有的操作，有助于处理图像边缘信息和保留细节信息。灰度级图像X的Top-hat变换可定义为

That(X)=X-(X∘De)

(18)

X的Bottom-hat变换定义为

Bhat(X)=(X·De)-X

(19)

式中：·为闭操作，∘为开操作，De为结构元素，本文采用半径为5的结构元素。

为验证计算整幅图像中每两个像素的有效性，使用仅结合灰度重构处理的FCM模型(GFCM)对图1进行聚类实验。其中，图1(a)为原始图像，图1(b)为真实图像。实验时，设置不同的窗口大小进行对比。以均方根误差(mean square error，MSE)作为衡量标准，其计算公式为

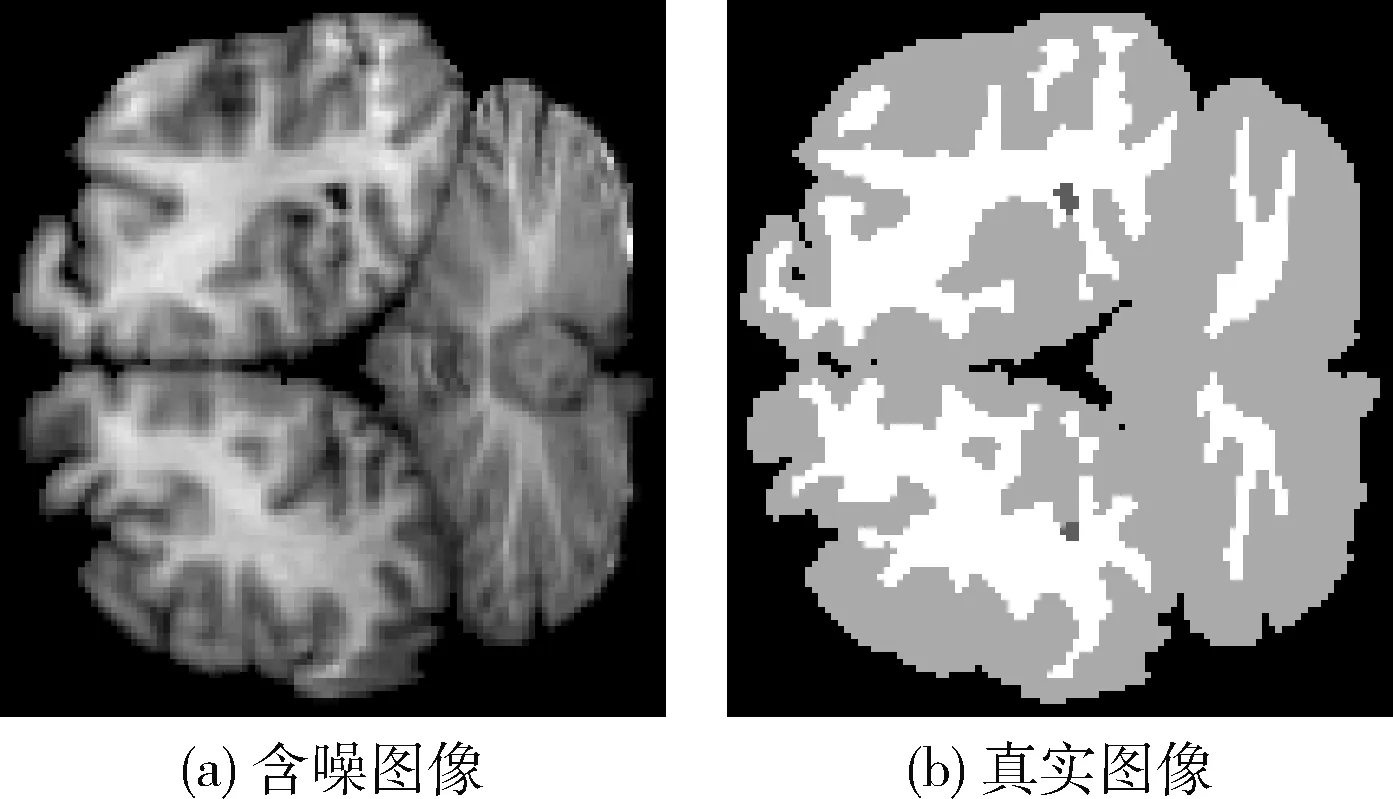
图1 性能验证实验源图像和真实图像

(20)

式中：Yk为算法取得的聚类中心，Bk为真实的聚类中心。MSE数值越小，则分割效果越好。

各个窗口对应的MSE见表1，根据数据可知，不恰当的窗口大小容易破坏图像的局部结构，从而产生不理想的分割结果。计算图像中每两个像素的相关信息获得的均方根误差最小，验证了所提方法的有效性。

表1 不同窗口下的均方根误差

2.2 改进的粒子群优化算法

PSO是一种基于种群的随机优化技术，被认为是一种全局搜索策略，得到了广泛应用[16]。在PSO中，种群中的每个成员称为粒子，代表优化问题的潜在解，被称为粒子群的每个成员代表优化问题的潜在解。种群P通过连续迭代进行演化，候选解的质量由相关联的粒子适应度值评估。对于每个粒子p有位置向量Zp=(zpr)p、速度向量Vp=(vpr)p、称之为该粒子最好位置的Pbest，并与邻域中发现的最佳位置的粒子相互作用，直至找到全局最优Gbest或者满足最大迭代条件。第t次迭代时，每个粒子都将根据式(21)和式(22)进行移动

Vp(t+1)=wVp(t)+Q1r1[Pbest(t)-Zp(t)]+

Q2r2[Gbest(t)-Zp(t)]

(21)

Zp(t+1)=Zp(t)+Vp(t+1)

(22)

其中，式(21)为速度更新公式，式(22)为位置更新公式，Q1和Q2是学习因子，r1和r2是介于(0，1)之间的随机数，w为惯性权重，当w值过大时，粒子速度过快，有更大的概率在全局空间寻优，当w值过小时，粒子速度过慢，有更大的概率在局部空间寻优。

进行图像分割时，前期主要对全局分割，有初始轮廓后再对细节部分进行分割，分割速度先快后慢，分割布局为先整体后局部，即快速进行全局寻优，慢速进行局部寻优。基于此思想提出一种自适应惯性权重，并用自适应权重替换介于(0，1)之间的随机数r1和r2，避免粒子寻优时陷入局部最优，确保粒子群算法与相应模型结合后，能够更加有效分割图像。改进后的惯性权重更新公式和速度更新公式如式(23)和式(24)所示

(23)

Vp(t+1)=wtVp(t)+(1-wt)(Q1(Pbest(t)-Zp(t))+

Q2(Gbest(t)-Zp(t)))

(24)

其中，t为从1开始迭代的次数，tmax为设置的最大迭代次数。惯性权重将根据迭代情况自适应调整，粒子速度也将自适应进行调整，可以更好平衡全局搜索和局部搜索，避免陷入局部最优。

2.3 提出的分割算法

应用SAPSO算法对GFCM的目标函数进行优化，提出一种FCM算法(SAPSOGFCM)。将聚类中心编码为粒子位置，对于P个粒子，有(c*P)个优化变量需要编码。第p的粒子的位置可以描述为Zp=(zp1，zp2，…，zpc)，其中，zpk(k=1，…，c)表示第p个解中的第k个聚类中心。适应度函数为

fp=JGFCM

(25)

(26)

其中，Z为粒子位置，即聚类中心，在算法中，最小化fp等同于最小化GFCM模型的目标函数。为了确保所有粒子在搜索空间内移动，最大位置和最小位置分别设置为图像的最大灰度值和最小灰度值。在式(2)的约束下，利用拉格朗日最小二乘法对隶属度求导，可得隶属度更新公式为

(27)

由式(27)可知，聚类中心确定后，计算隶属度，结合自适应的粒子群算法后，聚类中心通过自适应粒子群算法产生并进行寻优，隶属度和适应度值也随之进行更新。最后，根据输出的聚类中心和隶属度对图像进行分割。

所提算法流程见表2，通过给定的数值，先计算带宽H，进行灰度重构，再利用改进的粒子群算法优化的FCM模型进行图像分割。

表2 SAPSOGFCM算法流程

3 实 验

为了验证所提算法有较高分割精度和鲁棒性，使用Internet brain segmentation repository(IBSR)[17]中的数据集进行MR图像分割实验。IBSR是MR图像分割常用数据集之一，具有大量真实的脑MR图像，根据组成可分为两大类，第一类为不存在脑脊液图像，第二类为存在脑脊液图像，所有图像均含有噪声和不均匀度。在对不存在脑脊液的图像进行分割时，分割为白质和灰质，对存在脑脊液的图像进行分割时，分割为白质、灰质和脑脊液。同时，将所提算法与FCM、PRFLICM、FGFCM、FRFCM、PSOFCM及SAPSOFCM算法进行定量、定性分析对比。所选对比算法不仅可验证所提算法对噪声的抑制能力，还可验证所提算法对初始聚类中心的优化能力。

3.1 定量分析标准

定量分析时，采用Jaccard相似系数(JS)和Dice系数(DC)，对于一幅图像，如果M和G分别表示分割图像和真实图像，那么JS系数和DC系数可表示为

(28)

(29)

JS系数和DC系数值均在0与1之间，其值越大，分割效果越好。

3.2 分割实验

算法参数设置见表3。

表3 算法参数设置

3.2.1 不含脑脊液图像分割

本部分，分割类数设置为3，分别分割为背景、白质和灰质。

将分割结果可视化，如图2所示。其中，图2(b1)～图2(b3)分别为真实分割的整体、灰质和白质，图2(c)到图2(i)分别为FCM、PRFLICM、PSOFCM、SAPSOFCM、FGFCM、FRFCM、SAPSOGFCM，1到3分别为分割的整体、灰质和白质。从图中可看出所有算法均获得了良好的分割结果，对噪声都有一定的抗干扰性。但FCM、PSOFCM、FGFCM过多的将白质划分为灰质，SAPSOFCM、FRFCM、SAPSOGFCM效果相对较好。其中，SAPSOGFCM的取得的效果最好，如图中方框区域所示。同时，对分割结果进行定量分析，其JS系数和DC系数见表4。

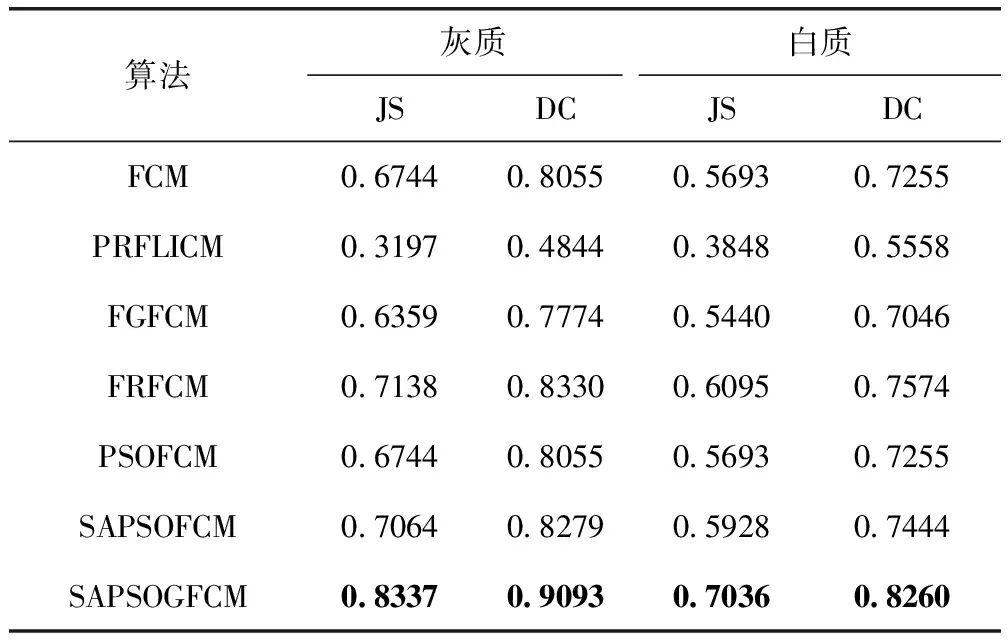
表4 不同算法的JS系数和DC系数

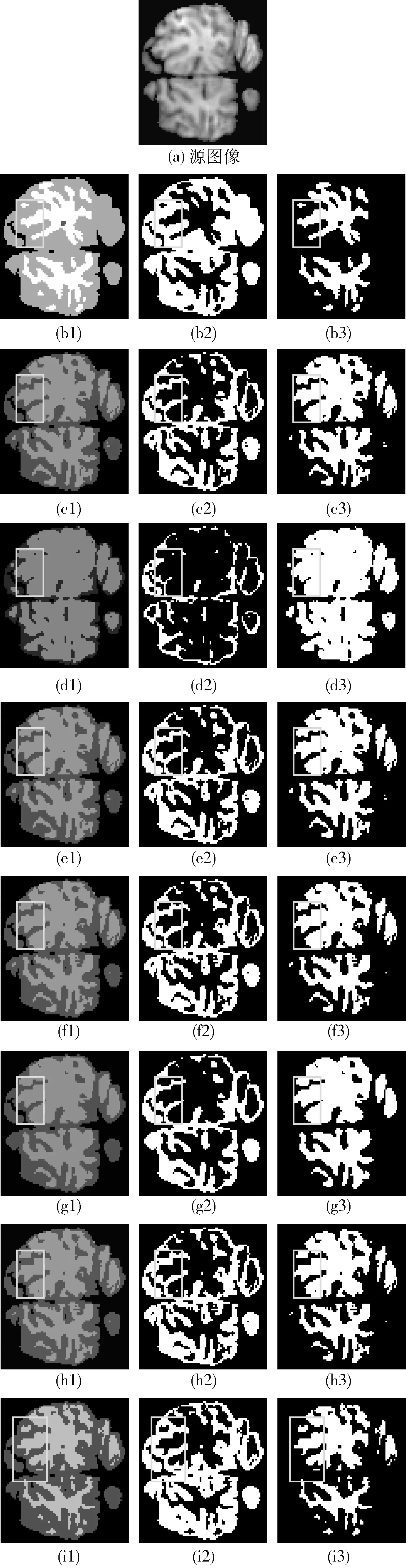
图2 实验1原始图像和分割结果

由JS系数和DC系数可知，FCM分割结果和PSOFCM分割结果相同。加入自适应策略的粒子群算法即SAPSO-FCM 的JS系数和DC系数均高于FCM和PSOFCM。所提出的SAPSOGFCM算法各项系数值均是最大，与定性分析中其错分率低相对应。

对同类型图像再次进行分割实验，实验结果可视化后如图3所示。其中，图3(b1)～图3(b3)分别为真实分割的整体、灰质和白质，图3(c)到图3(i)分别为FCM、PRFLICM、PSOFCM、SAPSOFCM、FGFCM、FRFCM、SAPSOGFCM，1到3分别为分割的整体、灰质和白质。FGFCM将白质过多的划分为灰质，FCM和PSOFCM的分割结果类似，FRFCM与SAPSOGFCM对白质的分割结果类似，SAPSOGFCM对灰质的分割效果明显接近于真实分割。对分割结果进行定量分析，其JS系数和DC系数见表5。

图3 实验2原始图像和分割结果

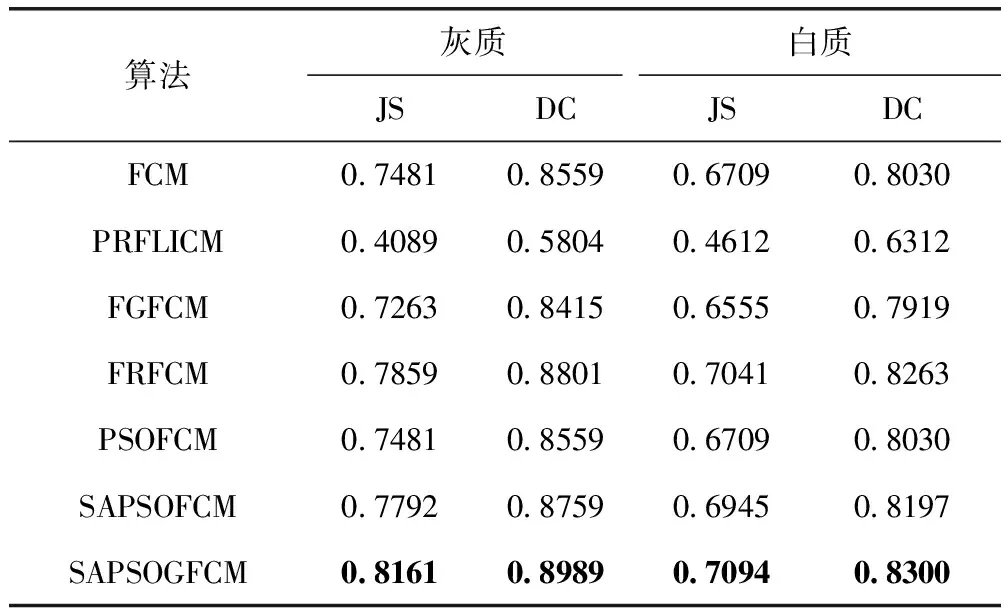
表5 不同算法的JS系数和DC系数

从表5中可知，SAPSOFCM的JS系数和DC系数值均大于FCM和PSOFCM的系数值，FRFCM的各项系数均大于SAPSOFCM。所改进的粒子群算法有效的同时仍不能达到最好效果，当与另一种策略相结合后即SAPSOGFCM，JS系数和DC系数皆得到提高。

3.2.2 含脑脊液图像分割

本部分，分割类数设置为4，分别分割为背景、白质、灰质和脑脊液。

实验结果可视化后如图4所示，其中，图4(a1)为源图像，图4(a2)为真实图像，图4(b1)～图4(b3)分别为真实分割的灰质、白质和脑脊液，图4(c)到图4(i)分别为FCM、PRFLICM、PSOFCM、SAPSOFCM、FGFCM、FRFCM、SAPSOGFCM，1到3分别为分割的灰质、白质和脑脊液。从图中可以看出PSOFCM对灰质的分割结果比FCM的分割结果更接近真实结果，SAPSOFCM与PSOFCM相比则更接近真实结果。PRFLICM、FGFCM和FRFCM的白质分割结果比SAPSOGFCM更接近真实分割。在灰质和脑脊液的分割中，SAPSOFCM的分割结果明显比其余算法的分割结果更为接近，尤其是脑脊液的实验结果。对脑脊液的分割效果均不理想，是由于图像噪声的影响，大量的脑脊液被划分为白质或灰质。实验结果的JS系数和DC系数见表6。

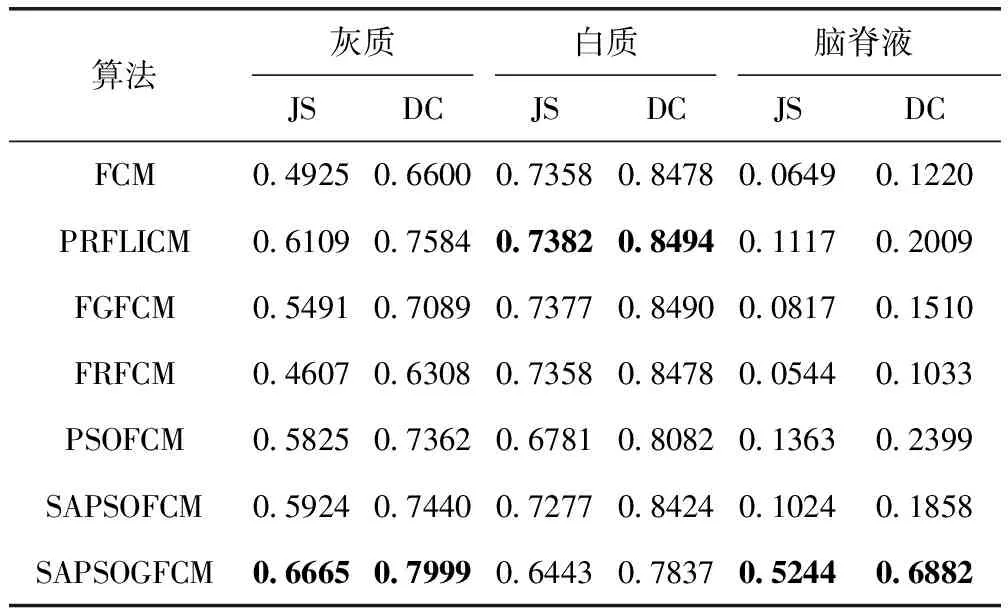
表6 不同算法的JS系数和DC系数

图4 实验3原始图像和分割结果

分析各算法的JS系数和DC系数可知，各算法在分割图像的不同区域都有明显优势，如PRFLICM在白质区域的JS系数和DC系数值最大。自适应粒子群算法优化的FCM与传统粒子群算法优化的FCM相比，整体上JS系数和DC系数值更大。所提出的SAPSOGFCM与上述算法相比，在灰质和脑脊液区域的JS系数和DC系数最大。虽然所提算法在白质区域JS系数和DC系数小于PRFLICM算法，但整体上所提算法系数值最大。

对同类型图像进行实验，分割结果可视化后如图5所示，其中，图5(a1)为源图像，图5(a2)为真实图像，图5(b1)～图5(b3)分别为真实分割的灰质、白质和脑脊液，图5(c)到图5(i)分别为FCM、PRFLICM、PSOFCM、SAPSOFCM、FGFCM、FRFCM、SAPSOGFCM，1到3分别为分割的灰质、白质和脑脊液。从图5中可看出，SAPSOFCM算法对灰质和脑脊液的分割结果与FCM和PSOFCM相比更接近真实结果，对白质的分割结果与PSOFCM的结果相比更接近真实分割。PRFLICM算法对白质的分割结果与另几种相比更接近真实结果。所提算法SAPSOGFCM对灰质和脑脊液的分割结果与其余几种相比更接近真实分割结果。实验结果的JS系数和DC系数见表7。

图5 实验4原始图像和分割结果

对比各算法的JS系数和DC系数，可知SAPSOFCM的各项系数均大于PSOFCM的系数。PRFLICM的白质分割JS系数和DC系数最大，在另两个区域的错分区域较大，系数值较小。SAPSOGFCM在灰质和脑脊液区域的JS系数和DC系数均大于其余算法的系数。

表4～表7中，不同算法的JS系数和DC系数存在明显差距，所提算法的JS系数和DC系数均取得较理想效果。与FCM、FGFCM、FRFCM、PRFLICM相比，所提算法不仅考虑噪声，而且还考虑了随机选取初始聚类中心的影响，与PSOFCM相比，自适应粒子群优化算法可以更好平衡全局寻优与局部寻优，从而取得更为理想的结果。

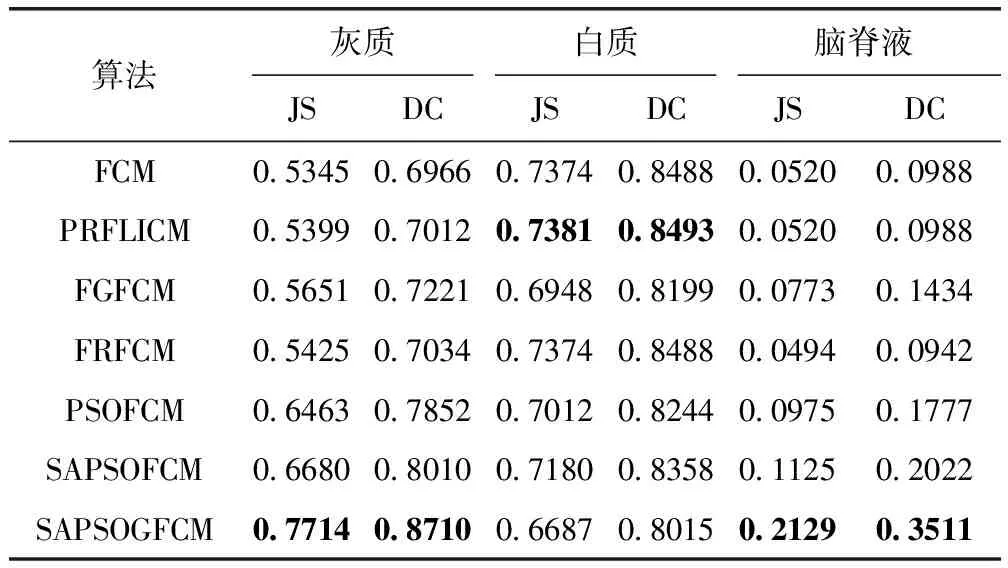
表7 不同算法的JS系数和DC系数

3.3 算法参数分析

与传统模糊C均值算法不同，本算法需要根据经验值设置粒子群优化算法中的参数和参数σ，为避免影响实验结果，根据文献[18]确定了粒子群算法的相关参数值。为评价参数σ对所提算法的影响，设定σ=[25,30,35,40,45,50,55,60]，分别对实验图像进行分割实验，对实验图像的白质DC系数进行统计，如图6所示。从图6可以看出，σ值对不同图像的影响程度不同，σ值的选取对实验结果有一定影响，但浮动较小，随之σ值增大，DC系数趋于稳定状态。σ值等于40时，4幅图像的DC系数有同一趋势，其余值的DC系数均在最大值附近波动。对于本文实验，选取σ=40，达到实验要求。对于不同算法，可根据需要取得的效果，适当增加σ值或减小σ值。

图6 不同σ值对应的白质DC系数

4 结束语

本文通过对原图像进行灰度重构，并对FCM算法的聚类中心进行优化，提出了一种FCM算法。利用IBSR数据集中的脑MR图像对所提算法进行验证，实验结果验证了所提出的灰度重构和改进的PSO算法的有效性，进一步验证了所提算法能更好抑制噪声和解决初始聚类中心影响分割结果的问题，取得理想的效果。但引入启发式算法后，FCM的计算复杂度变高，耗费时间增加。为此，下一步将针对复杂度进行改进，以减小运算时间。