立体车库载车器液压缓冲系统设计
2021-09-16陈小怡
陈小怡
(泸州职业技术学院,四川 泸州 646000)
引言
立体车库作为一种智能交通设备,具有便捷停车、空间利用率高等优点,解决了越来越多的市区商场停车难问题[1-3]。 立体车库载车器主要有电机升降控制和液压升降控制两种,在市场上正逐步推广[4-5]。在取车下降过程,常出现载车器过放现象[6],对车辆产生剧烈冲击振动,严重影响载车器升降平顺性。
为解决立体车库载车器过放冲击,王其松[7]研究了一种溢流阀缓冲式取车过放液压系统,基于AMESim搭建了系统仿真模型,得出减小溢流阀开启压力可降低缓冲腔压力冲击;季鹏[8]借鉴蓄能器缓冲原理设计了立体车库过放冲击再利用系统,利用AMESim分析了过放速度和蓄能器参数对冲击能回收系统的影响情况,得出过放速度增加应增大回收缸缸径或行程;冯铃等[9]提出一种立体车库过放节流缓冲系统,利用节流阀和溢流阀组合吸收载车器过放冲击,得出增大溢流阀设定压力或节流阀通径可减小过放缓冲位移。
上述技术研究对立体车库过放缓冲装置开发具有较好的理论指导,但过放缓冲位移可变,过放速度或质量变化对缓冲位移影响较大,导致缓冲定位不精准,影响载车器过放缓冲效果。基于此,本研究提出一种新型立体车库载车器液压缓冲系统,使用可变节流缓冲技术实现过放缓冲位移可控,给出了立体车库载车器可变节流缓冲原理,建立了立体车库载车器缓冲系统数学模型,基于AMESim搭建载车器可变节流缓冲系统仿真模型,研究了载车器液压缓冲系统缓冲特性,分析了过放速度、质量对系统缓冲特性的影响情况,仿真分析了载车器缓冲位移与节流阀过流面积函数的关系,并进行了缓冲系统试验验证工作,为立体车库载车器液压缓冲系统优化设计提供参考。
1 立体车库载车器液压缓冲机理
某商场立体车库如图1所示,立体车库载车器分布于不同的空间位置。取车时,载车器控制系统将车辆运至1层出口处。当控制系统失控时,载车器以一定速度撞向地面,即载车器发生过放事故[10-11]。

图1 某商场立体停车库
在1层地面取车处增设缓冲装置缓冲吸收载车器过放冲击,立体车库载车器液压缓冲系统原理简图如图2所示,缓冲板2表层镶有橡胶缓冲垫,尽可能减小载车器与缓冲板的接触冲击。载车器3过放时,吊绳4以一定速度持续下放载车器3,载车器3撞击缓冲板2,缓冲板2压缩缓冲液压缸8,同时缓冲板2触发控制器7工作,位移传感器5检测到载车器位移时,将其位移变化值传输至控制器7进行处理,进而转化为可调节流阀9的阀芯开度信号,使其阀芯开度实时调节,实现载车器3的缓慢减速和平稳制动,尽可能使载车器减速平滑无波动[12-14];缓冲结束后缓冲缸8复位弹簧支撑载车器复位。
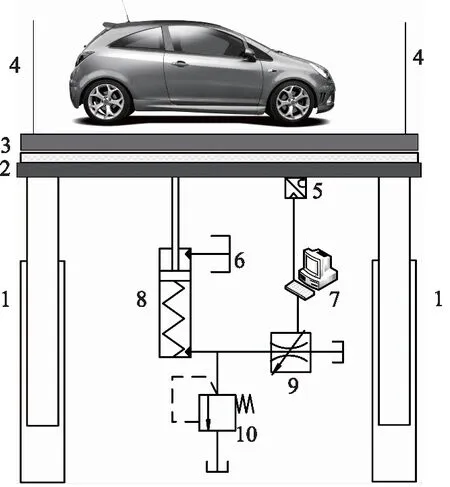
1.导向缸 2.缓冲板 3.载车器 4.吊绳 5.位移传感器6.油箱 7.控制器 8.缓冲缸 9.可调节流阀 10.过载阀图2 立体车库载车器液压缓冲机理简图
2 载车器液压缓冲系统数学模型建立
过放后,载车器初始冲击动能方程为:
(1)
式中,M—— 载车器总质量(包括车辆、吊绳等质量)
v0—— 过放初始速度
液压缸受载车器过放冲击,活塞力平衡方程为[15]:
(2)
式中,x—— 载车器缓冲位移
p—— 过放制动液压缸大腔压力
D—— 液压缸活塞直径
B—— 活塞滑动阻尼
节流阀流量Q方程为:
(3)
式中,C—— 节流系数
A(x) —— 节流阀过流面积函数
ρ—— 液压油密度,一般取850 kg/m3
3 载车器液压缓冲系统仿真模型建立
基于AMESim搭建如图3所示的立体车库载车器液压缓冲系统仿真模型,位移与阀芯开度信号用f(x)[16]表示,暂取f(x)为一次函数,令f(x)=-4x+0.8,由方程看出当x=0.2时,f(x)=0。
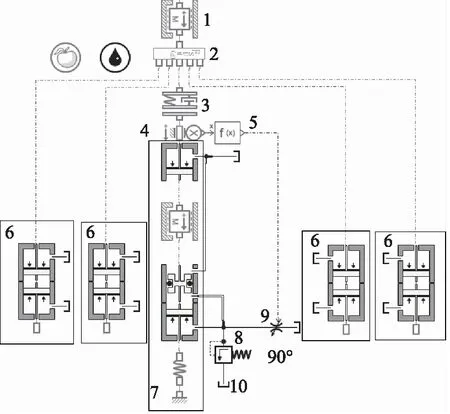
1.载车器模型 2.载车板模型 3.接触模型4.位移传感器 5.位移-阀芯开度函数 6.导向缸7.缓冲缸模型 8.溢流阀 9.变节流阀 10.油箱图3 立体车库载车器液压缓冲系统仿真模型
载车器液压缓冲系统参数按表1设置进行仿真。
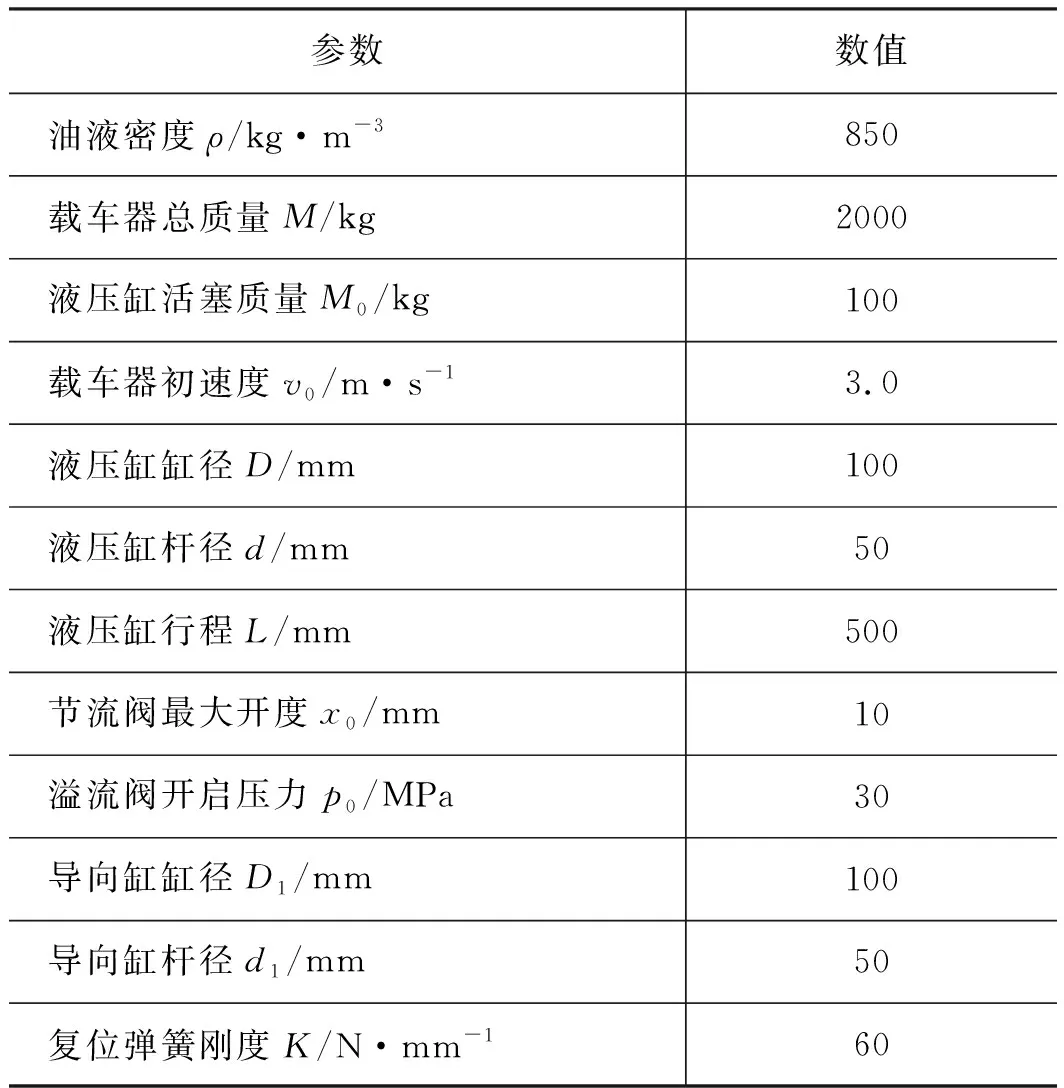
表1 仿真参数
4 立体车库载车器液压缓冲系统仿真
4.1 初始参数系统缓冲特性研究
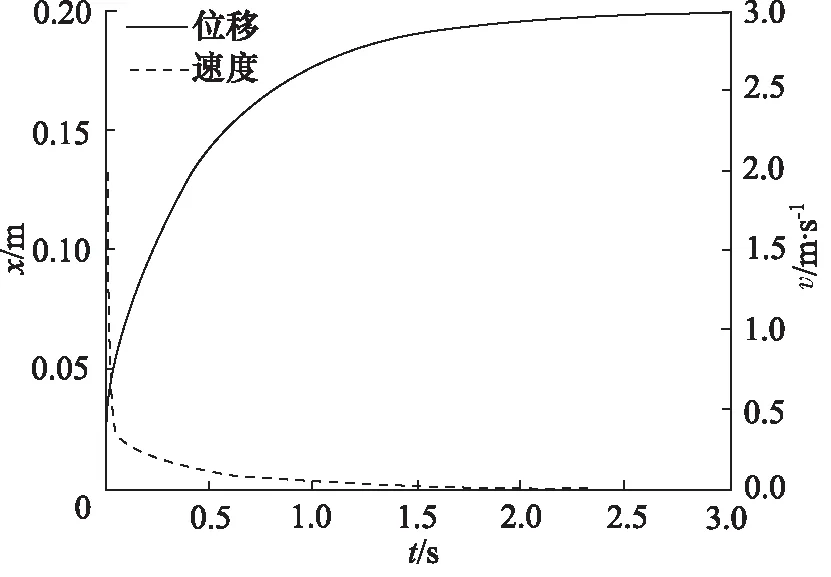
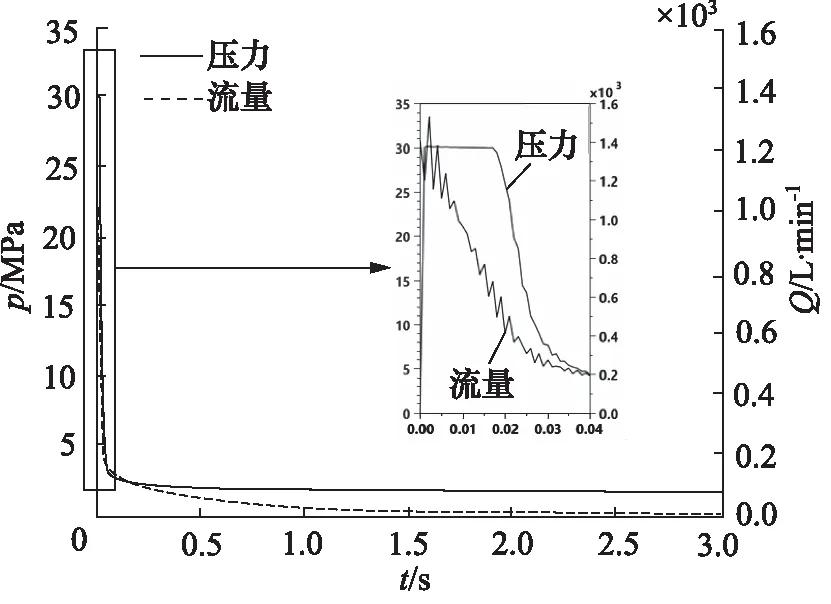
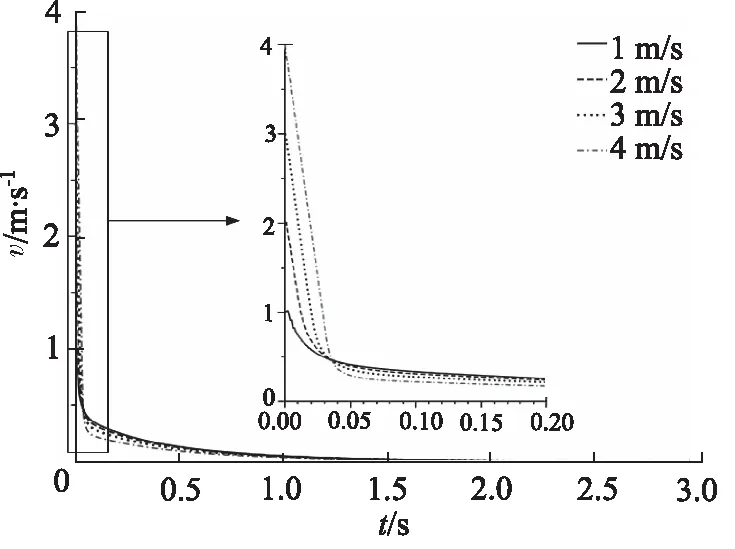
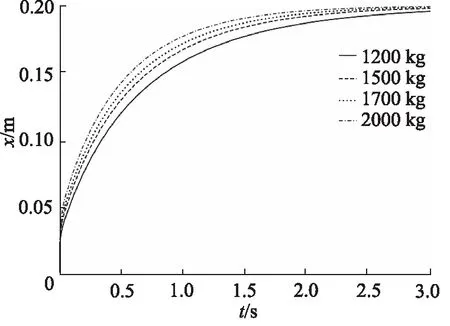
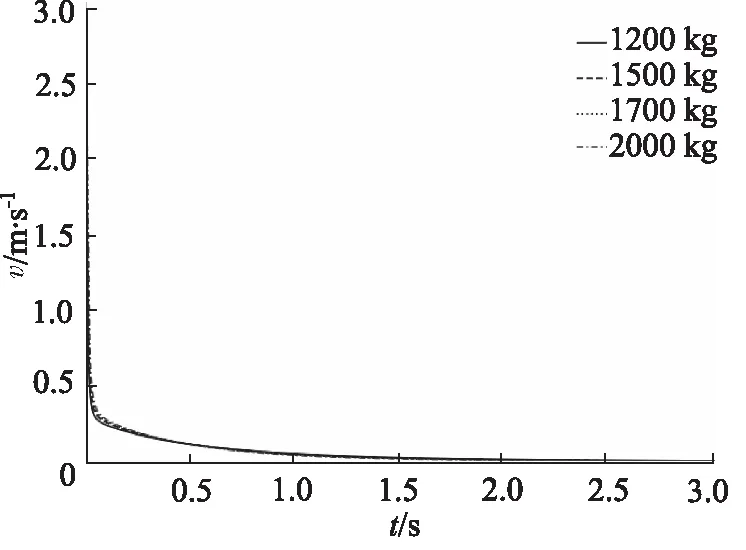
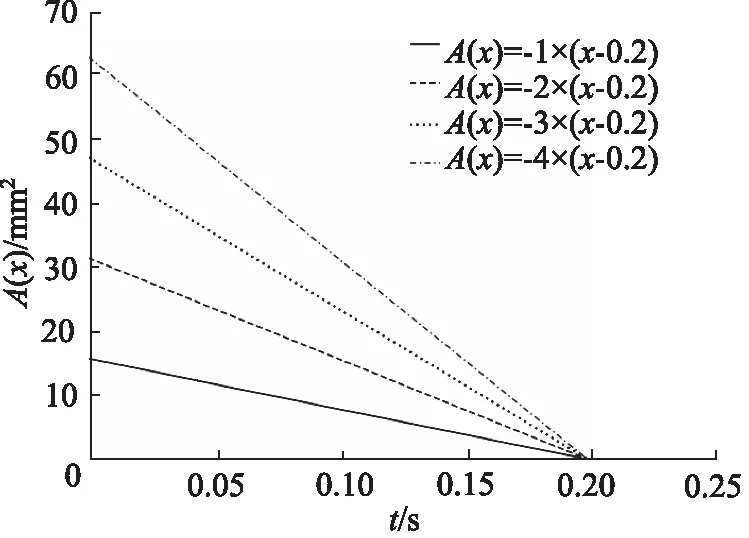
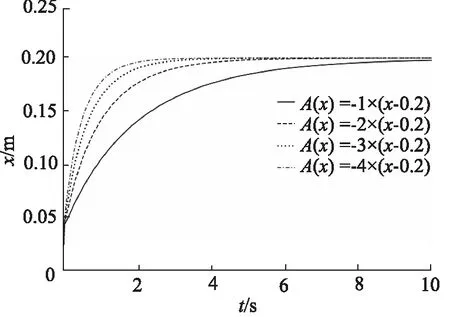
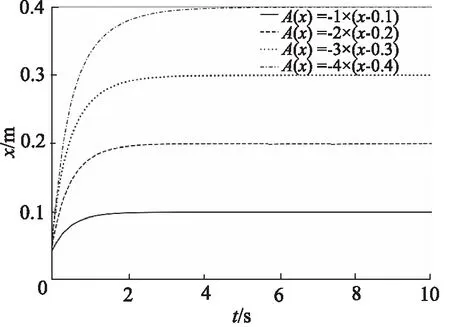
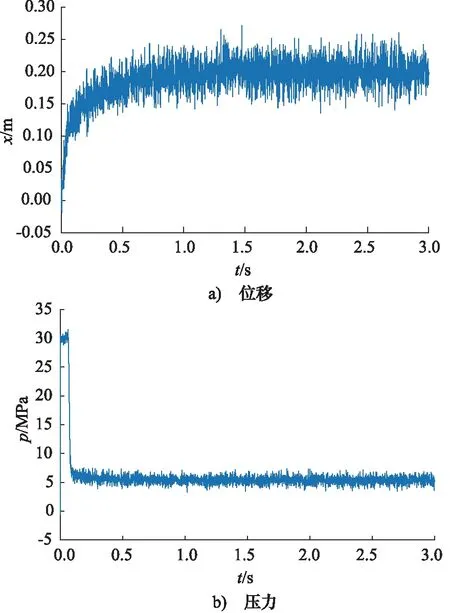
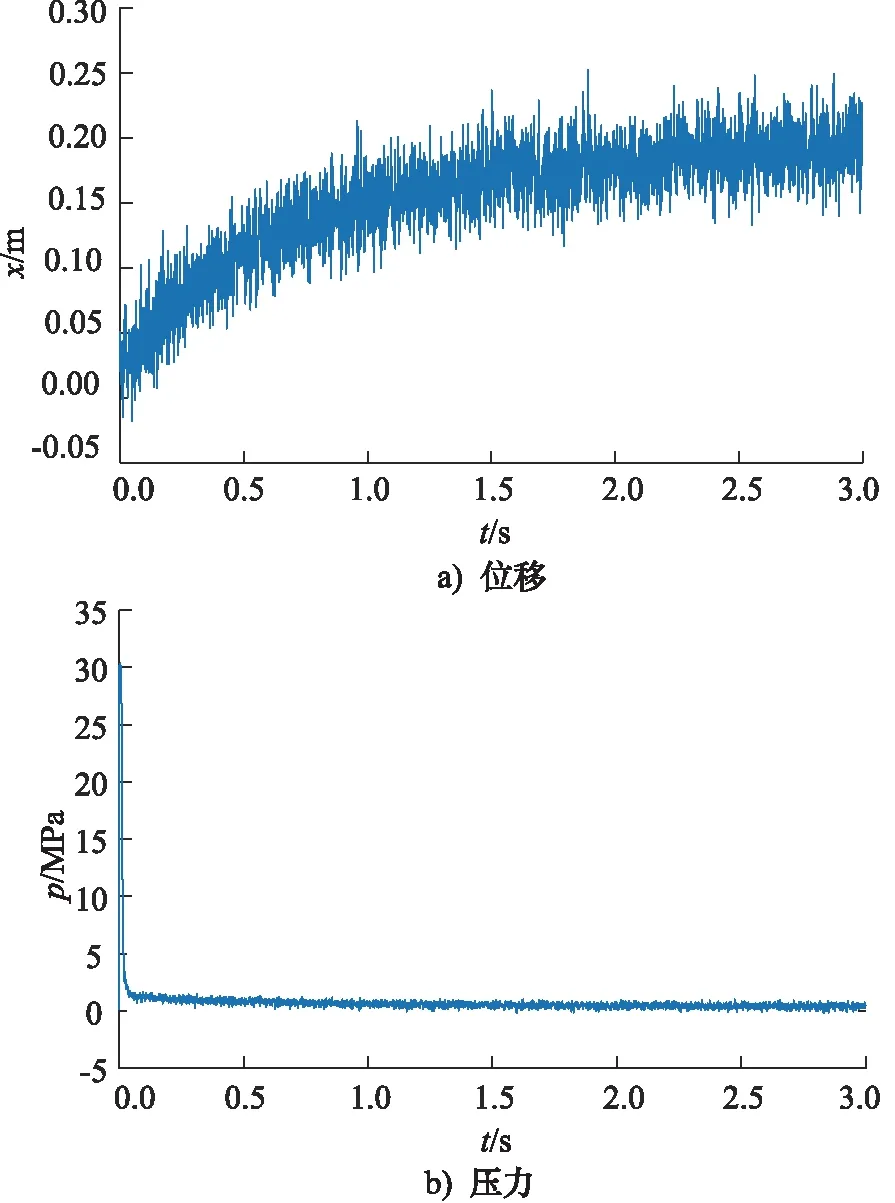
设置A(x)=f1(x)=-4x+0.8(0 图4 节流阀位移-过流面积曲线(一次函数) 仿真3 s得到载车器缓冲位移及过放速度变化曲线如图5所示,缓冲缸缓冲腔压力流量变化曲线如图6所示。 图5 载车器缓冲位移及过放速度变化曲线 图6 载车器缓冲缸缓冲腔压力流量变化曲线 从图5和图6看出:缓冲过程中,载车器速度先迅速降低,后缓慢减速直至停止;在0~0.02 s,载车器速度由3.0 m/s迅速减小为0.02 m/s;在0.02~3 s,载车器速度由0.02 m/s缓慢降至0 m/s,载车器过放缓冲结束后,载车器缓冲位移为0.2 m。 载车器速度为1.0, 2.0, 3.0, 4.0 m/s进行仿真分析,仿真得到载车器过放速度对载车器缓冲位移的影响曲线如图7所示,载车器过放速度对载车器缓冲速度的影响曲线如图8所示。 图7 载车器过放速度对载车器缓冲位移的影响 图8 载车器过放速度对载车器缓冲速度的影响 从图7和图8看出,当载车器过放速度由1.0 m/s增大至4.0 m/s时,载车器速度均先迅速降低,后缓冲减速停止,过放缓冲制动后,载车器缓冲位移均为0.2 m。显然,当载车器过放速度发生变化时,变节流液压缓冲系统能实现立体车库载车器精准缓冲。 载车器质量为1200, 1500, 1700, 2000 kg进行仿真分析,得到如图9所示的载车器质量对载车器缓冲位移的影响曲线和如图10所示的载车器质量对载车器缓冲速度的影响曲线。 从图9和图10看出,当载车器质量由1200 kg增大至2000 kg时,载车器缓冲位移为0.2 m,但小质量(M=1200 kg)时,缓冲过程持续时间延长,在3 s时,载车器缓冲位移还未达到最大值;载车器降速规律保持一致,速度先迅速降低后缓冲减速。与上节研究结论一致:当载车器质量发生变化时,变节流液压缓冲系统能实现立体车库载车器精准缓冲。 图9 载车器质量对载车器缓冲位移的影响 图10 载车器质量对载车器缓冲速度的影响 设置变节流阀过流面积方程表达式A(x)=k(x-0.2,k=-1,-2,-3,-4进行系统缓冲特性仿真,变节流阀过流面积与载车器缓冲位移关系如图11所示,仿真得到如图12所示的节流阀过流面积变化规律对载车器缓冲位移的影响曲线。 图11 变节流阀过流面积与载车器缓冲位移关系 图12 节流阀过流面积对载车器缓冲位移的影响 对于变节流阀过流面积A(x)=k(x-0.2),k=-1,-2,-3,-4,当x=0.2时,A(x)=0。从图11和图12看出,变节流阀最大过流面积增大时(由15.7 mm2增大至62.8 mm2),调整节流阀过流面积递减速率(k从-1调整至-4),过放缓冲后载车器缓冲位移相同,均为0.2 m。 按此结论,设置A(x)=k(x-0.1),k(x-0.2),k(x-0.3),k(x-0.4)(k取-1~-4)进行仿真验证,得到如图13所示的A(x)零点值对载车器缓冲位移的影响曲线。 图13 A(x)零点值对载车器缓冲位移的影响 由图13看出,当A(x)零点值分别为0.1,0.2,0.3,0.4时,载车器缓冲位移分别为0.1,0.2,0.3,0.4 m。显然,A(x)=0的零点值即为载车器缓冲位移值。 考虑到试验的难度,在实验室条件下进行立体车库载车器液压缓冲系统的试验验证,分别设定配重冲击质量为500 kg和1000 kg进行冲击试验验证,试验液压原理及装置如图14所示。 试验设备主要参数:液压缸选用缸径100 mm,杆径50 mm,活塞行程1.0 m;压力传感器输出电流信号4~20 mA,对应压力0~60 MPa;位移传感器输出电压信号0~10 V,对应位移0~1.0 m;比例阀电磁控制信号4~20 mA,对应阀口开度0~10 mm。 1.油箱 2.液压泵 3.泵溢流阀 4.配重电磁阀5.缓冲缸电磁阀 6.卷扬马达 7.绳盘 8.配重块9.卷扬绳 10.配重机架 11.活塞撞头 12.位移传感器13.控制器 14.数据采集显示器 15.压力传感器16.缓冲溢流阀 17.比例阀图14 实验室试验原理及设备 使用数据采集仪获得如图15和图16所示的配重为500 kg和1000 kg时的冲击数据。 由图15和图16可得,在500 kg和1000 kg配重冲击下,缓冲液压缸最大位移在(0.2±0.05)m范围内波动,缓冲腔缓冲压力在(30±2)MPa范围内波动,显然实验室试验对系统设计合理性及仿真结论真实性具有一定的验证支撑作用。 图15 M=500 kg配重冲击下的缓冲试验数据 图16 M=1000 kg配重冲击下的缓冲试验数据 基于立体车库载车器缓冲位移不精准问题,提出一种新型的立体车库载车器液压缓冲系统,根据载车器缓冲位移变化实时调整变节流阀过流面积实现了载车器缓冲位移可控,给出了载车器变节流缓冲机理,基于AMESim建立了立体车库载车器液压系统载车器过放缓冲模型,仿真了初始参数下的系统缓冲特性,分析了载车器过放速度和质量对系统缓冲特性的影响规律,研究了节流阀过流面积变化及其零点值对系统缓冲特性的影响情况,并进行了系统缓冲性能试验验证,仿真得到以下结论: (1) 变节流缓冲过程,载车器速度先迅速降低,后缓冲减速可实现较精准的缓冲定位; (2) 变节流阀过流面积变化规律不变,载车器缓冲位移不受载车器过放速度和质量影响; (3) 增加大开度节流阀阀口关闭速率与降低小开度节流阀阀口关闭速率能获得相同的载车器缓冲位移; (4) 变节流阀过流面积方程式零点值对应载车器缓冲位移值; (5) 试验数据对仿真结论具有较高的支撑验证作用。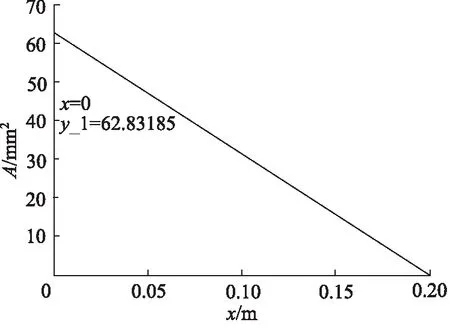
4.2 载车器过放速度对系统缓冲特性影响

4.3 载车器质量对系统缓冲特性影响
4.4 变节流阀过流面积变化规律影响
5 试验验证

6 结论
