城市轨道交通车辆检修与运用的关系研究

侯妍君，沈建文，申樟虹，郭 然

(北京市市政工程设计研究总院有限公司，北京 100082)

轨道交通在客流输送方面承担着越来越重要的角色，随着出行客流量的不断上升，乘客出行需求与车辆运输能力的耦合关系也更为紧密。城市轨道交通经过长期运营，制定了严格的检修规程，以保证列车的安全运营[1]。当列车的运营里程积累到一定里程数，列车就到达了检修周期，若车辆同时到达检修周期：一是增加车辆基地同时检修的任务量，车辆基地的检修任务将呈现不均衡性，使维修效率降低[2]；二是大量车辆送修，运营线路车辆减少，难以完成当日运输计划，导致乘客滞留[3]。为预防上述情况发生，列车不能同时到达检修周期，也是为了保证列车的累计运行里程呈现阶梯状分布。因此，精准排布列车运用计划显得尤为重要。

关于车辆运用排布计划，国内外学者进行了大量研究。国内传统城市轨道交通列车运行图的排布，编组人员依赖经验及列车运行里程，每日根据客流、运能等不同需求，采用二分格手动完成列车排布[4]。此过程需耗费大量的人力物力，编制周期长，且编制质量得不到保证，车辆仍会出现欠修或过修情况[5-6]。国外学者对动车组、铁路车辆的案例进行研究，对比考虑检修对动车组运用计划的影响，得到考虑检修的运用计划有利于减少车辆维修费用的结论[7-8]。

城市轨道交通各条线路的列车由运用车、备用车和检修车组成[9-11]。在线路运营初期，检修车和备用车的总和不宜低于总配属车的20%，远期不宜低于15%[12]。基于列车检修周期研究车辆运行排布计划，可控制不同车辆到达检修的时间，有利于车辆段的工作任务安排，有利于车辆更加合理的应用，甚至可以减少检修车数量或避免车辆的欠(过)修问题，从而减小项目的投资和运营成本。

1 模型建立

分析目标：为避免大量列车同时到达检修周期，需分析列车每日运行里程，确保列车运行里程出现稳定差值，使列车的每日运行计划更加科学合理。文中对列车每日运行计划进行分析，给出列车每日运行计划建议。

1.1 工况一

假设该运行图仅包含列车出库、正线运行、列车入库的运营组织模式。即所有车辆在正线上，从始发站至终点站单一交路行驶，如图1所示。

图1 线路运行情况一

根据客流需求计算出每日需运行次数及运用车数量，定义参数如表1所示。

表1 参数定义

首先，所有列车需完成每日运行任务，有

a1+a2+a3+a4+…+aN=A

(1)

当列车首次到达检修周期，且a1到达检修里程时，a1已经持续运行D天，则满足

a1LD=R

(2)

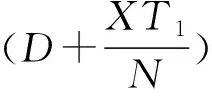
(3)

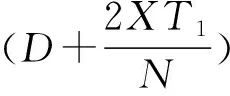
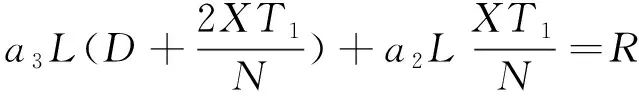
(4)

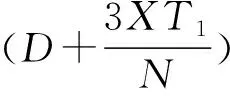
(5)

……

(6)

为保证a1和aN的周期不重合，有

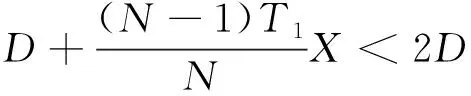
(7)

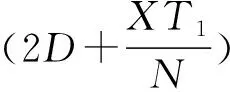
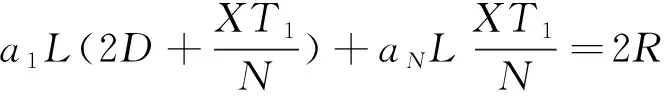
(8)

1.2 工况二

根据交路需求，假设该运行图包含大小交路，线路运行一周会出现2种情况，如图2所示。

图2 线路运行情况二

根据客流需求计算出每日需运行次数及运用车数量后，新增或变更参数定义(见表2)。

表2 参数更新及补充定义

首先，所有列车需完成每日运行需求，有

a1+a2+a3+a4+…+aN=A

(9)

b1+b2+b3+b4+…+bN=B

(10)

当第1组车到达检修里程时，第1组车已持续运行D天，则满足

(a1L1+b1L2)D=R

(11)

(12)

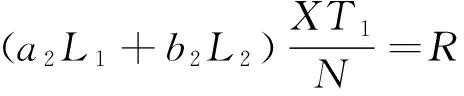
(13)

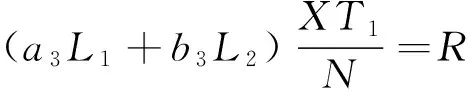
(14)

……

(15)

为保证a1和aN的周期不重合，有

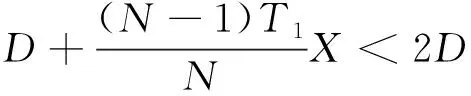
(16)

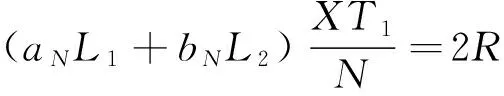
(17)

2 案例分析

某城市轨道交通线路，采用单一交路运营，沿A站、B站、C站、D站的顺序行驶，全长27.3 km，共配置10列车，其中7列为运用车、2列为检修车、1列为备用车[13]。由于该线路为专用线路，非通勤线路，该线路的列车排布较为均匀，且不存在早晚高峰情况。已知该线路每日需运行178次，除早上车辆出库、晚上车辆回库外，不存在车辆频繁出入车辆段情况。

2.1 算例

将某城市轨道交通线路车辆分为5组，计算列车的每日运行任务计划。代入情况一的算式中，即X=10列，N=5组，A=89圈，L=54.6 km，利用mathmatica进行计算，计算步骤如图3所示。

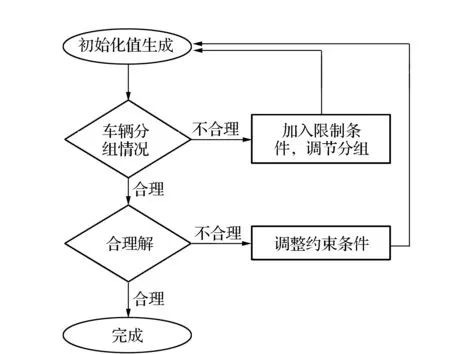
图3 模型计算具体步骤

当列车到达第一次月修时，运行结果如图4所示。

图4 第一次到达月修运行结果

当列车第二次到达月修时，运行结果如图5所示。

图5 第二次到达月修运行结果

同理，代入架修、大修，具体如图6、图7所示。

图6 到达架修运行结果

图7 到达大修运行结果

架大修与月修相互嵌套、逐层递进，经历了若干次月修后，车辆将达到架修周期，经历4次架修后车辆到达大修周期。将上述计算结果进行汇总，如表3所示。

表3 不同阶段、不同组别车辆对应每日运行周期

初始运行周期为30 d，按照表3的第1行完成运行。按照月修的运行周期，每运行一次单组车到达运行时间会滞后2 d。按照表3第2行运行16个周期后，每组列车的运行时间相差34 d，按照上述计划需求，此时将5组列车均匀排布运行，即每列车每天运行约18圈，持续周期约为35 d即可将首组列车送至架修。为更便于理解，用表4表示上述列车的运行形式。

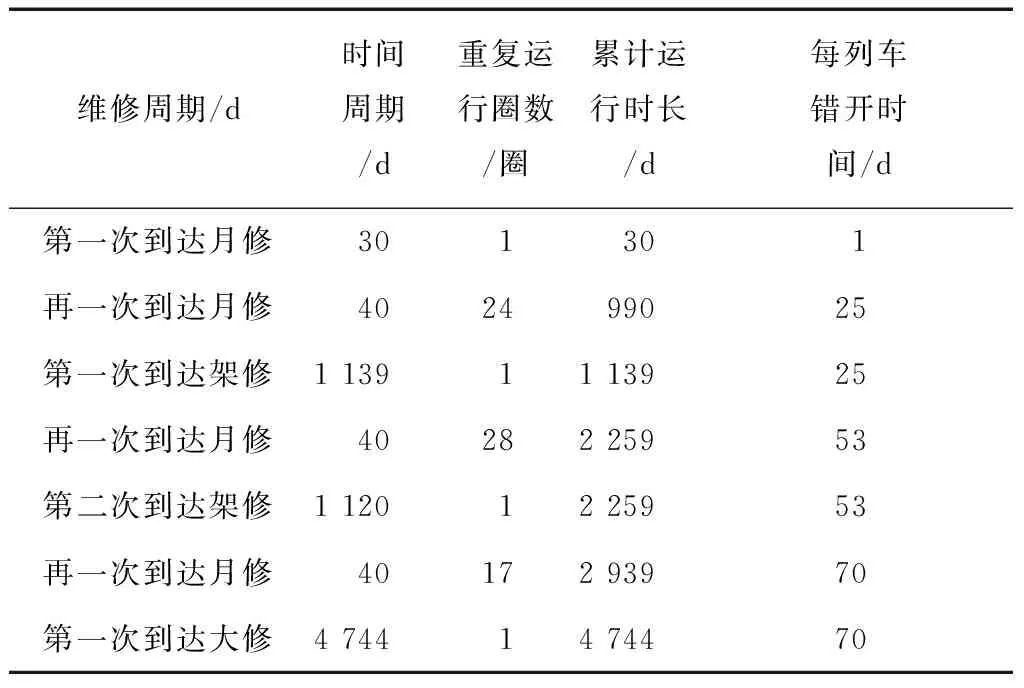
表4 车辆月修、架修关系

根据表4可知，该线路配置车辆可满足线路目前运行需求。若列车的错开时间无法满足架修、大修的停修时间需求，即每列车错开时间<列车检修时间，则需调整该线路的配车数。若列车的错开时间可满足架修、大修的停修时间需求，即每列车错开时间>列车检修时间，当某列车的检修时间出现延迟，可在占用每列车保持相同任务量运行时间期间内调整。

由表4可知，将上述次数代回公式进行验证，可验证架修对应的每列车每日运行计划为月修每日运行计划平均数。因此，按照上述计划运行，可检修间隔的稳定性。若某天调整某车辆的运行次数，保证该列车在一段周期内的运行平均次数，即可保证列车运行间隔的稳定性。

2.2 分析

通过对该线路的调研，该线路已经持续运营10余年，101～107号车目前的运行里程已经超过260万km，108～110号车的运行里程较短[14-17]。因此，在车辆大修时，应考虑101～107号车的检修需求比较迫切。2021年，同时会有3列车进入大修阶段，将影响既有线路上的列车运行效率。

若按照上述理论排布，101/102号车每日运行23圈，103/104号车每日运行19圈，105/106号车每日运行17圈，107/108号车每日运行16圈，109/110号车每日运行14圈，在运行至30 d时，101和102号车到达月检周期。若根据表3的运行计划排布列车，则最多同时存在2列车到达月修、架修或大修，且不存在列车欠(过)修问题。根据表4可知，月修至架修仍存在149 d的优化时间，即上述排布可达到仅存在一列车到达月修，可将列车到达月修时间完全错开。同理，架修至大修仍有1 805 d的优化时间，则最多同时存在2列车进入架大修，避免目前3列车同时到达大修的情况发生。

根据上述排布理论分析，该线路设置10列车的数量合理，满足现阶段每6min发车间隔的使用需求。检修车比例应严格控制在20%以内，当有2列车进入大修时，剩余8列车可满足该线路的使用需求。若3列车同时进入大修，剩余7列车存在过度使用情况，需考虑增加购置1列车，以降低车辆过度使用情况。因此，经过优化排布，虽不影响该线路整体配车数量，但可使列车的任务分配更加合理。

3 结 语

为保障城市轨道交通的正常运行，需在车辆基地配置相应的检修设备以满足车辆检修的使用需求。由于列车的检修周期与运行公里数呈现强相关，因此，文中的研究重点是根据列车的运行里程，将该条线路上的多列列车每日上线运行次数进行排序，以保证列车有序到达检修周期，进而避免多列车同时到达检修周期。基于本理论可将线路上的车辆进行自动化排布，作为智能车辆段的子系统，实现对列车运行计划的自动化排布。

由于验证案例为非通勤线路，列车数量较少，影响行车组织的因素较少，可采用本算法进行基本计算及验证分析。考虑到城市轨道交通的既有线路中存在工作日、周末及节假日线路客流分布变化较大的情况，对列车运行次数会有不同需求，因此，在本模型上增设其他相关参数和约束，进一步丰富模型的普遍性和适用性。