全轴转向半挂铰接车辆通过性优化及验证

喻 娟，王俊勇，周 胜，张陈林，钟汉文

(1.西南交通大学 机械工程学院，四川 成都 610031；2.湖南中车智行科技有限公司，湖南 长沙 410006)

缓解交通压力、减少空气污染已成为城市发展亟待解决的问题，在全民提倡低碳出行的大趋势下，公共交通运量需求逐年攀升。为了更好地适应城市快捷、高效的运输需求，半挂铰接车辆应运而生。但因传统半挂铰接车辆转向不灵活、通过性差、安全性低，其应用受到限制[1-3]，造成这些问题的主要原因之一是由于内轮差过大，且随着轴距的增加，内轮差现象愈发凸显[4-6]。

为解决半挂铰接车辆的内轮差问题，提高轨迹的跟随性能，国内外学者针对半挂铰接车辆转向技术展开研究。邓欣涛等[7]通过分析计算发现，对半挂铰接车辆后轴施加一定角度能有效减小内轮差。聂枝根等[8-9]提出一种针对不同工况切换模式的半挂车后轴主动转向控制策略，以满足车辆在不同工况下的稳定性需求。代馥光[10]利用模糊控制和差动制动方法对半挂车辆的路径跟随控制展开研究。田晋跃等[11]将半挂车第三轴设计成随动桥，有效提高了车辆的轨迹跟随能力和转向机动性。Yang、Abroshan以及Bai等[12-14]提出了一种包含模糊控制及PID控制的路径跟随控制，在保证车辆通道宽度的同时改善车辆的横向稳定性。Cheng等[15]为减少挂车尾部的轨迹偏移、提高车辆侧倾稳定性，提出了一种最优线性二次控制算法。Ozkan等[16]采用遗传算法，对基于铰接角的后轮随动转向机构进行优化，降低了车胎磨耗。

综上所述，国内外学者主要通过对挂车后轴的转向控制来减小内轮差、提高车辆的跟随性能，但却少有关于轨迹跟随精度优化方面的研究。半挂铰接车辆的全轴转向技术，不仅能极大提高车辆通过性、降低轮胎磨耗，而且其优良的转向控制特性使车辆具有低速机动性高、高速稳定性好的特点[17-19]。

周胜等[20]针对全轴转向双铰接车辆，提出以通道宽度最小为目标的一阶延时转向方法，实质上是以铰接点轨迹偏移量作为控制目标。优化后的最大轨迹偏移量为0.8m，但其结果是基于简化数学模型计算而得，并未进行多体动力学仿真分析。

文中针对全轴转向半挂铰接车辆，通过建立基于一阶延时控制策略的运动学模型，求解车辆各轴的运动轨迹。以轨迹跟随最优为优化目标，优化一阶延时可变参数，并采用Simpack和Simulink的联合仿真方式，进一步验证该策略的有效性。

1 全轴转向半挂铰接车辆运动学模型

车辆运动状态不仅受速度及转角影响，还受轮胎侧偏、路面激扰及车身侧倾等因素影响，因此，为便于分析，需简化运动学模型。假设半挂铰接车辆以低速匀速状态转向，忽略由轮胎变形产生的侧偏力，各车辆单元的运动保持在同一水平面内，且不考虑垂向运动。为求解半挂铰接车辆的运动轨迹，如图 1所示，取牵引车前轴中点A、后轴中点B、铰接中心点J及挂车轴中点C，构建半挂铰接车辆的单轨运动学模型。

图1 半挂铰接车辆运动学模型

根据笛卡尔坐标规定，建立如图1所示的地面坐标系X-O-Y及车辆坐标系x1-o1-y1和x2-o2-y2，车辆坐标系原点位于各车辆单元的质心处。针对单轨车辆模型，令牵引车前轴A为第一轴，牵引车后轴B为第二轴，挂车轴C为第三轴。将牵引车和挂车的车体视为变形量可忽略不计的刚体，则牵引车前后轴轴距为L，铰接中心点到牵引车后轴和挂车轴的距离为Lm、Lt，且均为常量。各轴均可主动转向，δi(i=1,2,3)为第i轴相对车身的转向角，φ为半挂车铰接角，规定各转角方向以逆时针为正，顺时针为负。

已知第一轴速度为v1，由速度投影定理[21]可分别求得第二、第三轴速度为v2、v3。基于地面坐标系，由车辆运动学模型，将速度分解到X、Y轴上，推导公式为

(1)

式中：vux和vuy(u=1,2,3 )分别为车辆第u轴的速度在地面坐标系X轴、Y轴上的分量；δu为车辆第u轴的转向角；Φw(w=1,2 )为车辆航向角，w=1时为牵引车航向角，w=2时为挂车航向角。

(2)

当t=0时，各轴初始坐标分别为(L+Lm+Lt，0)、(Lm+Lt，0)和(0，0)。对式(1)中各速度分量积分，可求得半挂铰接车辆的轨迹方程为

(3)

以某半挂铰接车辆为例，该车辆基本参数如表1所示。

表1 某半挂铰接车辆基本参数 m

由上述运动学方程可绘制出车辆各轴的运动轨迹。作为全轴转向车辆，为实现第二轴、第三轴对第一轴的轨迹跟随，需对转向角δ2、δ3的跟随规律进行探究。

文献[20]对第一轴恒定转角转向的单体车进行研究，通过分析车辆在弯道进入阶段和稳态转向阶段的运行姿态，得出了后轴跟随的条件公式。运用等价无穷小、差分改写、Z变换等方法进一步推导条件公式，结合控制连续性和工程化应用方面的考虑，最终得到轨迹跟随理想转角的近似拟合函数，一阶延时转角方程为

δj(tn)=kj1×δj(tn-1)+kj2×(-δ(j-1)(tn-1))

(j=2,3)

(4)

式中：kj1为取值范围在(0,1)的可变参数，kj2=1-kj1。

根据一阶延时转角方程，可得到如图 2所示的可变参数kj1在不同取值下的车辆运动轨迹(xi(t),yi(t))。

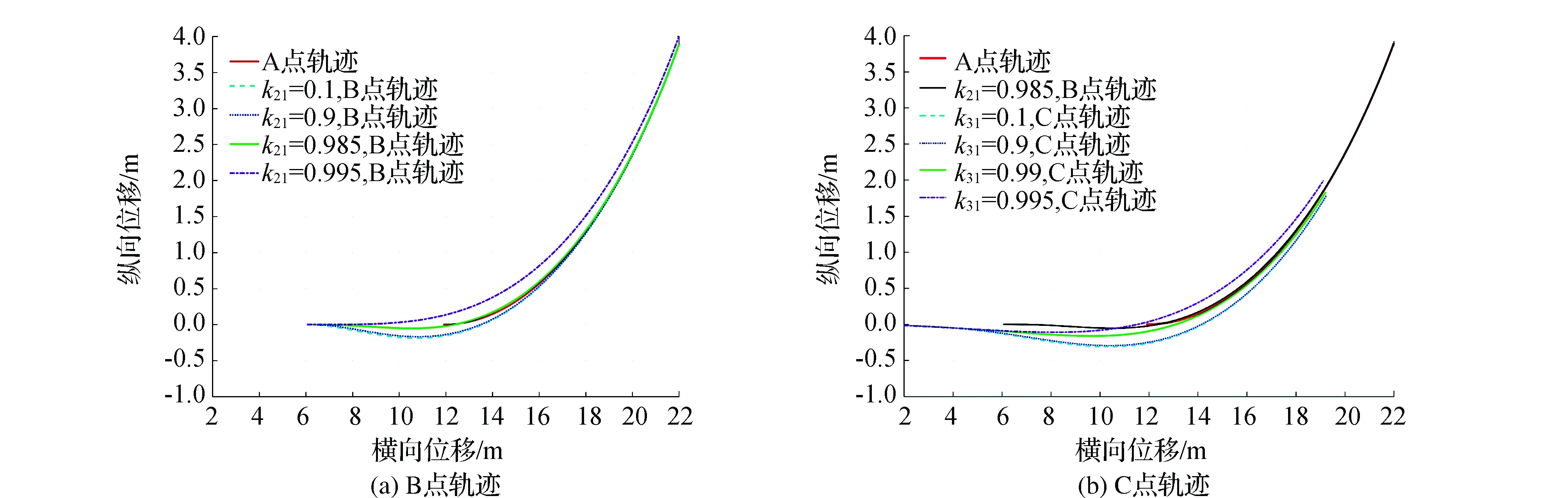
图2 一阶延时控制策略下的车辆轨迹

经分析，一阶延时转角方程可变参数kj1的取值在很大程度上影响车辆的跟随性能，进而影响车辆通过性，且第三轴可变参数k31的理想取值随第二轴可变参数k21的取值变化而变化。为进一步提高车辆跟随精度，需对可变参数kj1(j=2,3)的最优值做进一步探究。

2 一阶延时可变参数优化分析

以半挂铰接车辆第二轴相对第一轴的轨迹跟随为例，在一阶延时转向控制策略下，第一轴、第二轴中点轨迹的一般运动规律如图 3所示。

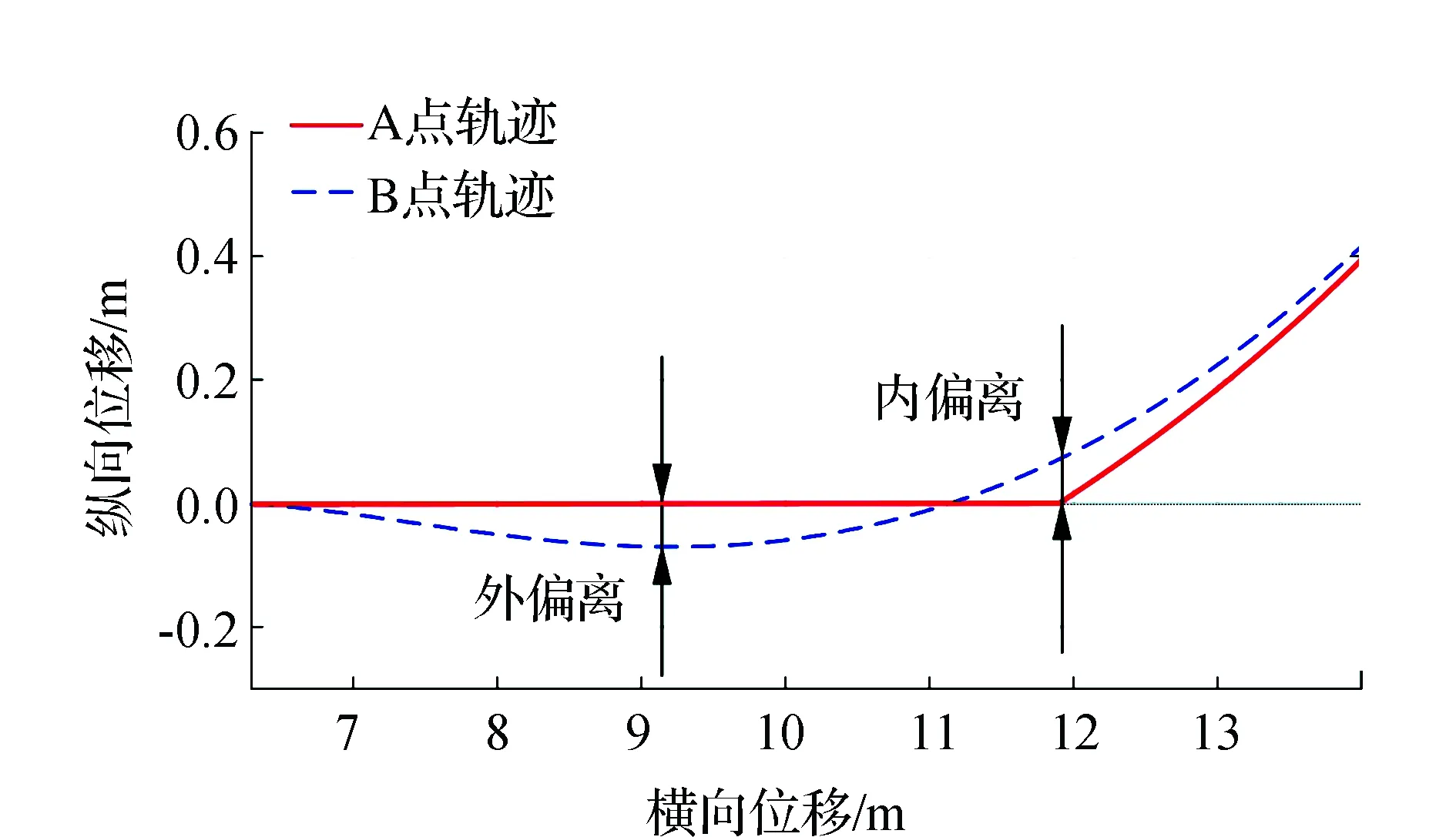
图3 轨迹偏移

(5)

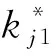
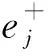
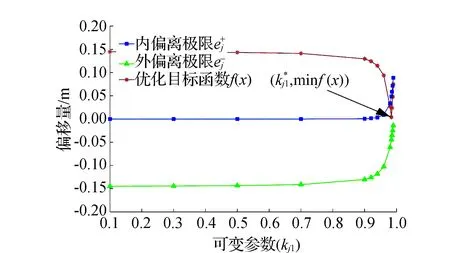
图4 偏移量随kj1增大的变化趋势

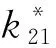
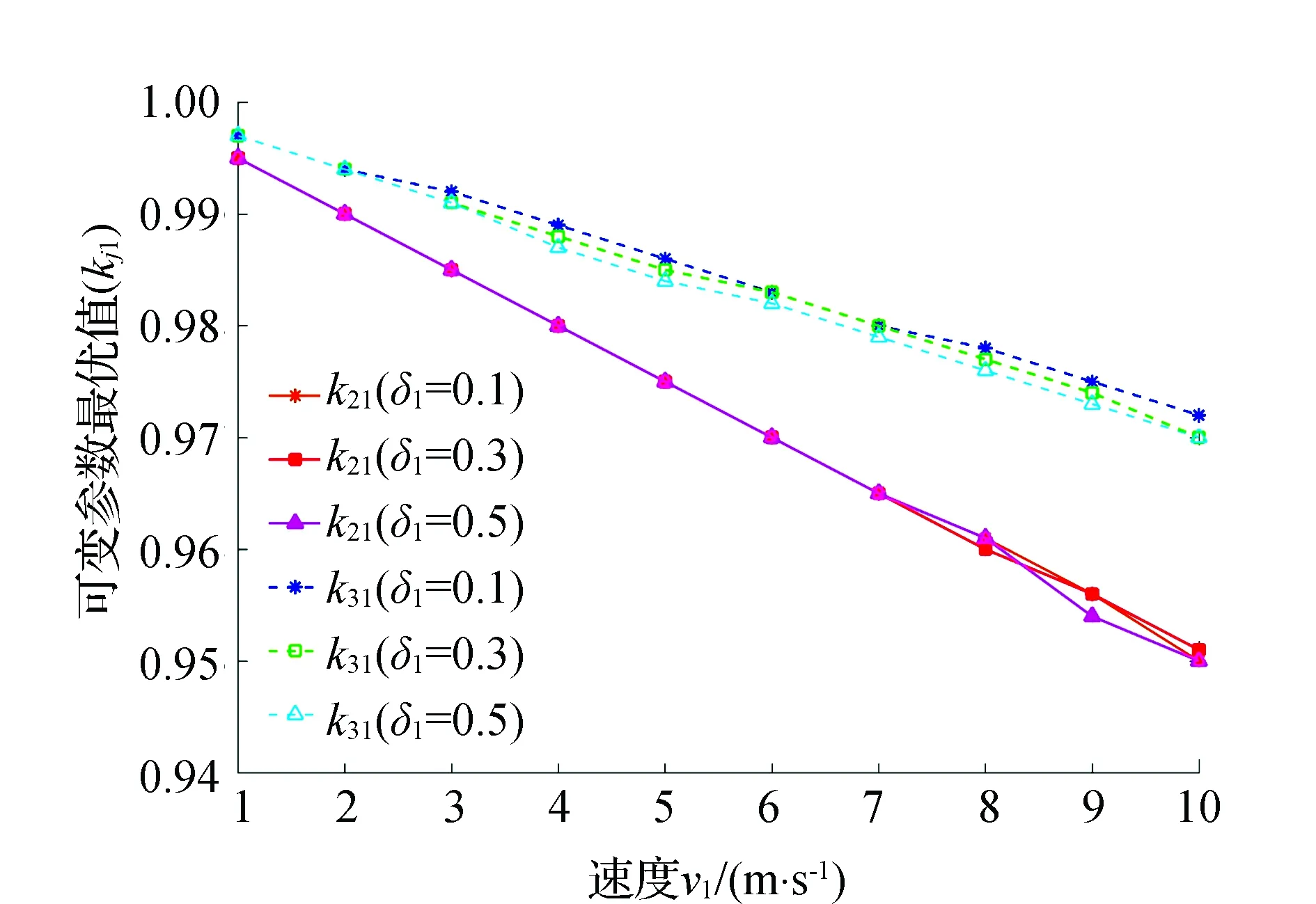
图5 不同工况下一阶延时可变参数最优值变化规律

皮尔逊相关系数(Pearson Correlation Coefficient，简称PCCs)用于度量2个变量间的相关性，定义2个变量间协方差和标准差的商[22]。算式为

(6)

PCCs为介于-1到1之间的值，当2个变量的线性关系增强，相关系数趋于1或-1。根据以上数据，对同一转向角下的6组数据进行分析计算，可得到各组数据的PCCs，如表2所示。

表2 第二轴、第三轴在不同工况下的PCCs

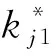
(7)

式中：aj，bj(j=2,3)为线性函数系数。

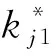
对比图 2可知，转向工况下参考优化后车辆具有优良的轨迹跟随性能。车辆通道宽度减小的同时通过性得到提高,后轴速度始终沿弯道切线方向，有效降低了轮胎磨耗，延长使用寿命。此外，研究是以车辆低速行驶为前提，路面激扰、车身侧倾等因素对车辆运动状态的影响可忽略不计。

3 基于Simpack的虚拟样机仿真验证

虚拟样机技术在工业工程领域的产品设计开发过程中占据重要地位。在缩短开发周期、节约成本的同时，它还能更加切实有效地反映系统的各项性能及应用状态。

通过对数学模型的分析计算及优化，最终得到的车辆运动轨迹能体现出优异的轨迹跟随性能。但理论数学模型中的工况趋于理想，不能真实反应实际运用中控制策略的有效性、可行性。为了使该控制策略的实用性得到进一步验证，现采用Simpack和Simulink联合仿真的方式展开分析。

以表1中所示的某半挂铰接车辆为例，在Simpack中搭建车辆运动学模型，转向工况设置为R30 m无缓和路段180°弯道。考虑到模型运算速度及仿真的准确性，根据验证目的适当简化模型，车辆模型的结构拓扑关系如图7所示。

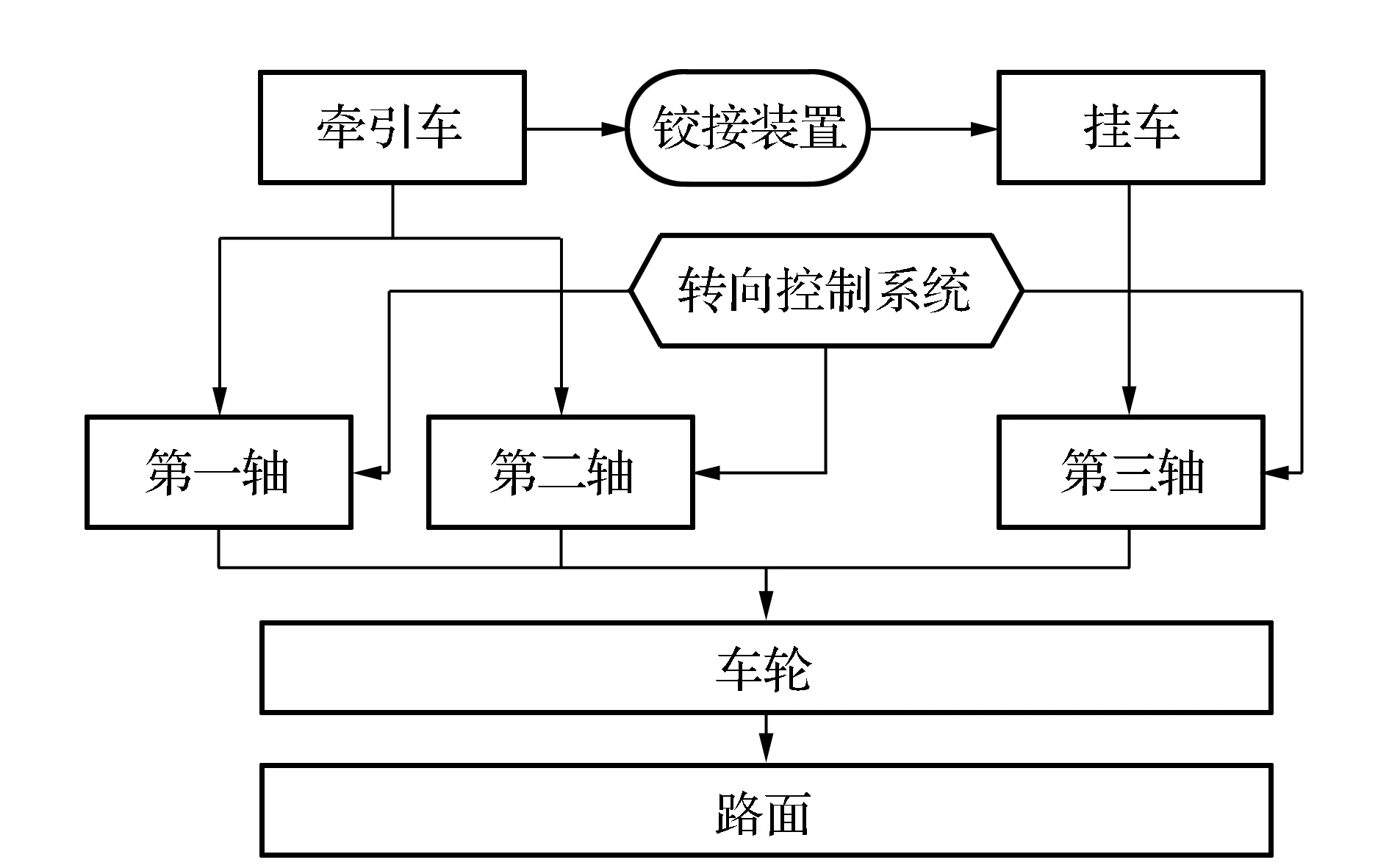
图7 半挂铰接车辆模型结构拓扑

为实现车辆的轨迹跟随，该模型中半挂铰接车辆第一轴转向由软件自带的虚拟驾驶模式控制，该模式可使车辆沿预设线路行驶。第二轴、第三轴的跟随转向角δ2(t)、δ3(t)可根据Simpack动力学模型实时交互数据，经Simulink计算而得，图 8为联合仿真原理。

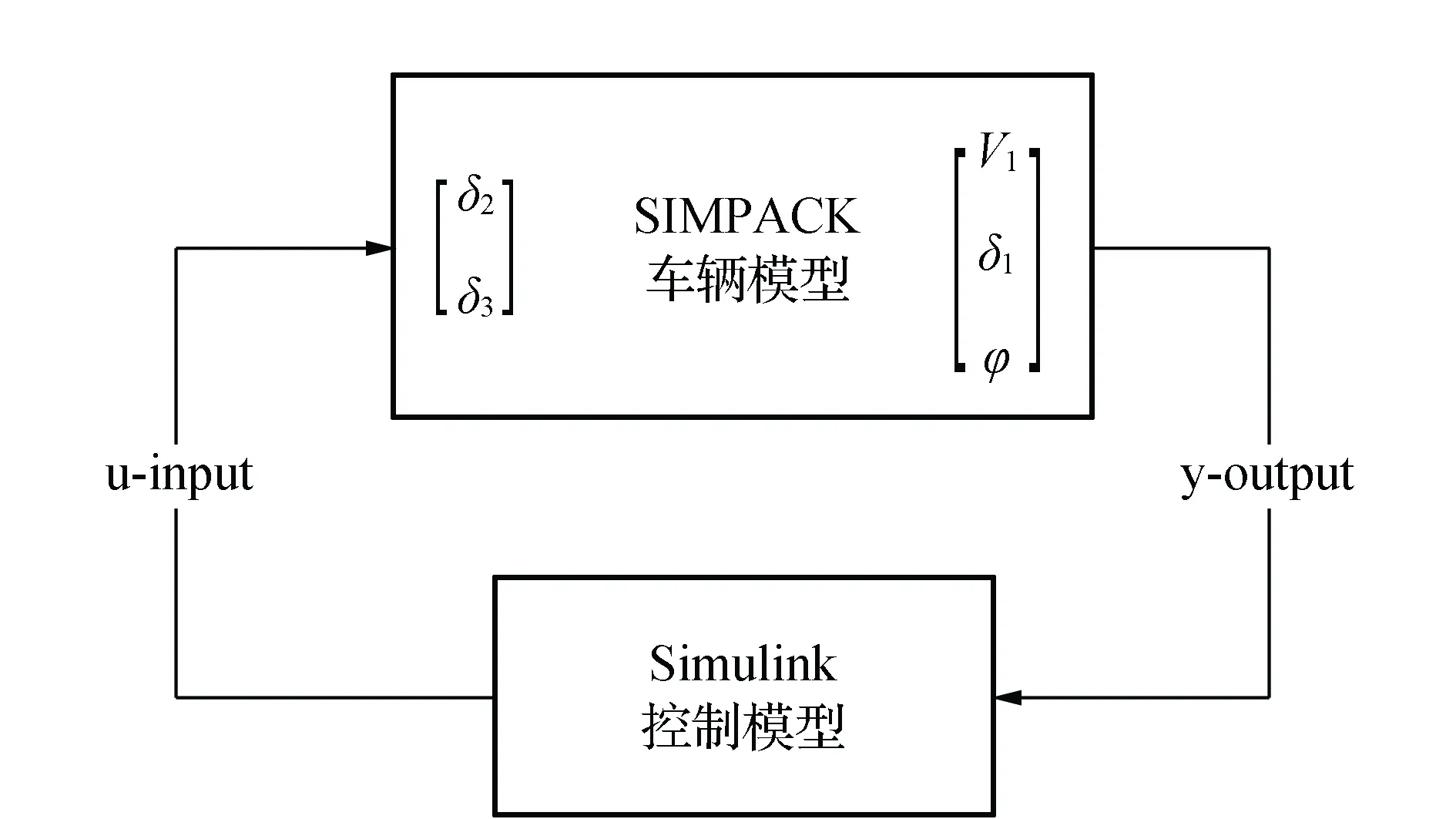
图8 联合仿真原理

联合仿真结果如图9所示，对比传统前轴转向，采用文中所示控制策略转向的车辆运行姿态，发现在相同转向工况下(见图 9(a))，传统前轴转向车辆在转弯过程中，车身未能保持在通道限界内，车头右侧超出规定限界，通道宽度更宽，车辆通过性更差。并且第一轴轨迹相较于既定线路向弯道外侧偏移，车辆的操纵稳定性、转向灵活性更差。

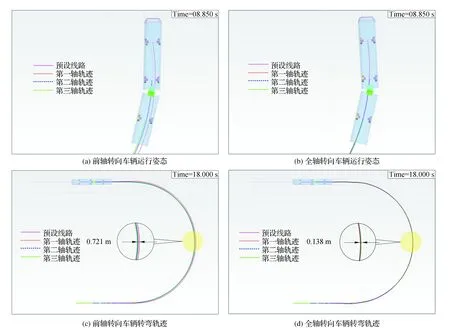
图9 联合仿真结果

而对于采用参数优化后的一阶延时控制策略的半挂铰接车辆而言，上述问题都得到了有效改善，如图 9(b)所示。

如图 9(c)、(d)所示，对比两种转向模式下的车辆轨迹，传统前轴转向车辆的最大轨迹偏离在弯道中段，偏移量为0.721 m。而采用一阶延时控制策略的全轴转向车辆最大轨迹偏移量为0.138 m，缩小了约80%。此外，采用以上优化控制策略针对双铰接车辆[20]进行同等工况仿真，最大轨迹偏移量仅为0.574 m，在已有研究基础上提升了28%。

综上所述，参数优化后的一阶延时控制策略可行性得到进一步证实，并且全轴转向使半挂铰接车辆存在的通过性、转向灵活性问题得到了明显改善。

4 结 语

为改善半挂铰接车辆的内轮差问题、提高通过性，在车辆运动学模型的基础上，对一阶延时可变参数的优化展开研究。经分析可知，跟随最优参数与一轴转角无关，与一轴速度呈线性相关。采用Simpack和Simulink联合仿真方式，进一步验证了该控制策略的可行性。仿真结果表明：采用参数优化后的一阶延时控制策略的半挂铰接车辆与前轴转向车辆相比，轨迹偏移量降低约80%。对比车辆转向姿态可以发现，全轴转向车辆的通过性、转向灵活性都优于传统前轴转向。该研究为半挂铰接车辆通过性的改善提供了理论支持，也为方案的后续工程化应用提供数据参考。