基于正交有限元法的轮对压装影响因素研究
2021-09-16朱博文路永婕王建西
朱博文,路永婕,王建西,孙 英
(1.太原中车时代轨道工程机械有限公司,山西 太原 030027;2.石家庄铁道大学,河北 石家庄 050043;3.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,河北 石家庄 050043;4.石家庄铁道大学 教育部道路与铁道工程安全保障重点实验室,河北 石家庄 050043;5.中车太原机车车辆有限公司,山西 太原 030027)
1 轮对注油压装理论计算
1.1 最大结合压力
根据产品图样,查询《铁道车辆用LZ50钢车轴及钢坯技术条件》(TB/T 2945—1999)可知,LZ50车轴的屈服强度σs为345MPa;查询《铁路货车用辗钢整体车轮》(TB/T 2817—2018)及参考文献[7],CL60车轮的屈服强度σs为351 MPa;车轴、车轮弹性模量为E=206 GPa,泊松比γ=0.3[8-9],轮座公称尺寸d=194 mm,车轮直径公称尺寸D=840 mm。在不产生塑性变形条件下,轮对的最大结合压力算式分别为
1)车轴
P轴max=0.5σs
(1)
2)车轮
P轮max=aσs
(2)
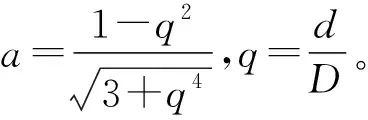
通过计算得出P轴max=172.5 MPa,P轮max=191.750 MPa。所以,在不产生塑性变形条件下,其最大结合压力为172.5 MPa,满足《机车轮对组装技术条件》(TB/T 1463—2015)中注油压装油压不大于170 MPa的规定。
1.2 注油油压计算
轮毂和轮座接触应力为
(3)
式中:δ为过盈量,取值为0.175~0.213 mm;εW=1(实心轴)。
(4)
通过计算可得Pkmin=89.664 MPa;Pkmax=109.134 MPa。注油油压Pm=1.1Pk[10],Pm∈[98.630,120.047]MPa,即理想状态下理论注油压力为120.047 MPa。考虑轮轴形位公差、过盈量等因素,经试验验证可知,在轮对压装工艺实际中注油压力为140 MPa时为宜。参考同类型不同产品轮对,轮对压装过盈量应为0.175~0.291 mm,理论注油油压为98.405~164.008 MPa。
1.3 油压对车轮直径变化量影响
不同注油压力引起的车轮直径变化量计算式为
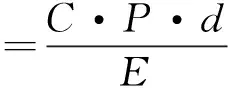
(5)
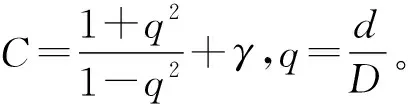
计算当注油压力分别为130 MPa、140 MPa、147 MPa、170 MPa、172.5 MPa时车轮最小直径变化量,如表1所示。

表1 车轮毂孔直径变化量
2 轮对注油压装过程有限元仿真
为验证有限元模型的正确性,将理论计算结果和仿真结果进行对比,根据产品图纸建立轮对注油压装有限元模型。在模拟轮对注油压装时,轮、轴配合面的接触应力呈现环向均匀分布,因此,注油压装的过程模拟可简化为轴对称模型,从而提高计算效率、降低计算规模。在研究过程中,研究对象为轮、轴配合面的接触问题,由于配合面其他部位对研究对象影响极小,因此可对其进行忽略简化[11-12]。
文中主要研究有限元接触问题,且模型为轴对称模型,车轮、车轴均采用由4个节点构成的四边形双线性非协调轴对称单元CAX4I[13-15]。单元最小边长为1 mm,远离接触区域的网格划分逐渐增大,最大为5 mm,共约10 580个单元;车轮毂孔的圆柱度为0 mm,通过几何近似方法模拟车轴轮座圆柱度为0.025 mm;过盈量为0.2 mm(理论注油压力为107 MPa);冷压过程摩擦系数为0.13,油膜下摩擦系数为0.025。仿真注油压装过程可分为4个阶段:第一阶段为初始压装阶段,车轮向压入方向前进22 mm,初步建立接触关系,在润滑油膜作用下摩擦系数设为0.025;第二阶段为冷压阶段,匀速压入至52.5 mm,该过程中无高压油,摩擦系数为0.13;第三阶段为注油压装阶段,此阶段压入至204.5 mm,在其配合面施加注油压力,摩擦系数变为0.025;最后阶段为撤去压力、位移。仿真结果如图1、图2及表2所示,图3为真实注油压装曲线。

图1 车轴轮座圆柱度为0时仿真轮对注油压装曲线
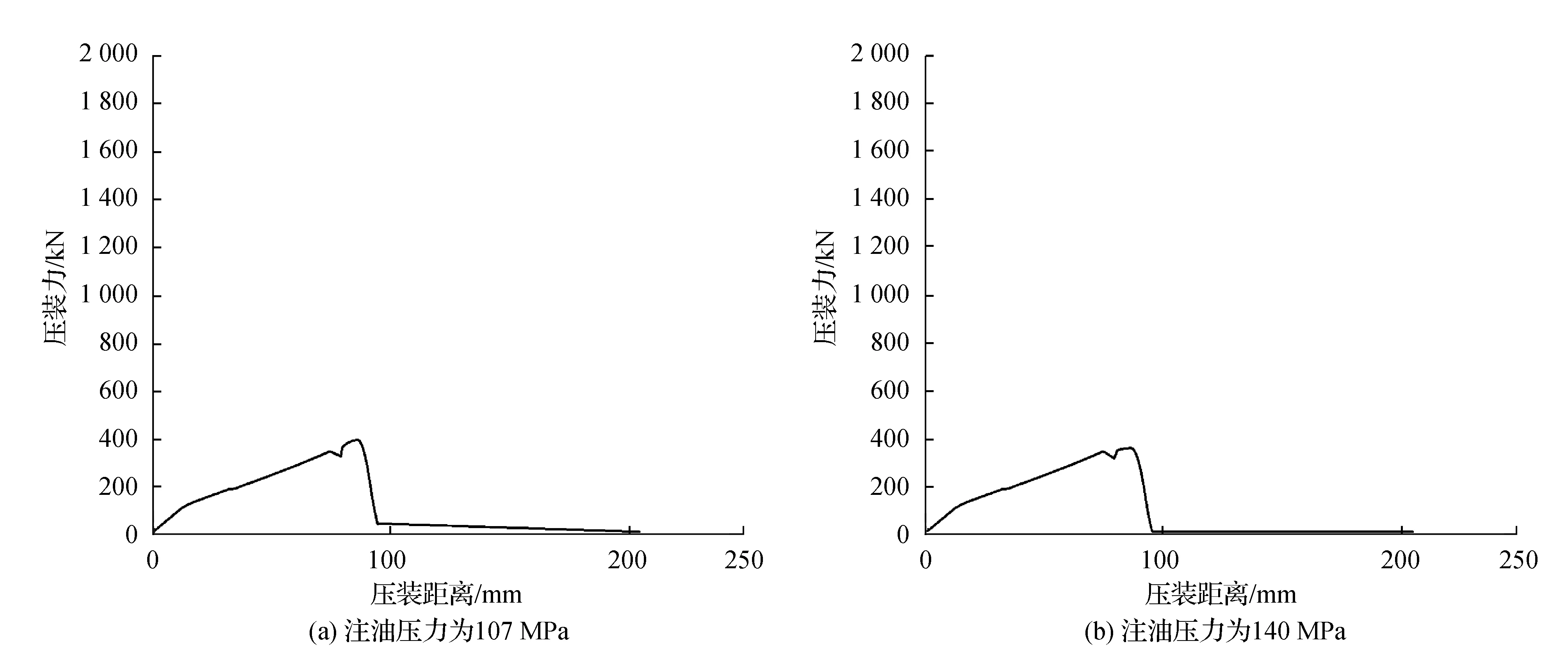
图2 车轴轮座圆柱度为0.025时仿真轮对注油压装曲线
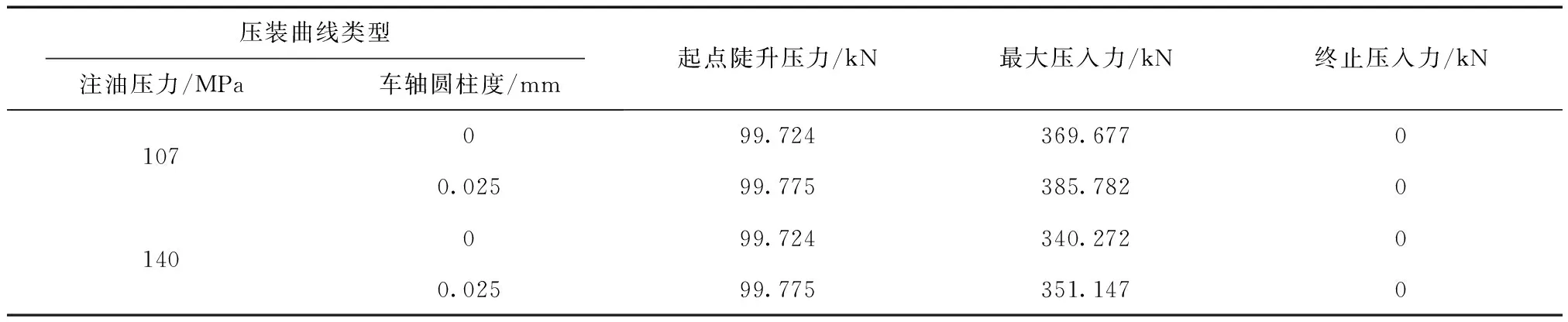
表2 仿真压装曲线数据

图3 实际注油压装曲线
将仿真曲线与实际压装曲线进行比较,从图1、图2及上面的计算结果对比发现:
1)注油压力施加:有限元仿真计算轮对在压力为140 MPa时车轮直径变化量为0.183 mm,理论计算结果为0.186 mm,两者误差为1.613%,小于工程误差5%的要求,因此,注油压力设置准确。
2)注油压装曲线:有限元仿真注油压力为107 MPa时,计算得到CFN的最大压入力为369.677 kN(圆柱度为0)、385.782 kN(圆柱度为0.025 mm);注油压力为140 MPa时,最大压入力为340.272 kN(圆柱度为0)、351.147 kN(圆柱度为0.025 mm);实际压装曲线中最大压入力为354 kN,与带有圆柱度140 MPa注油压力下的仿真计算结果351.147 kN的误差为0.812%,小于工程误差5%要求,有限元计算模型准确。
图1、图2中仿真压装曲线与图3中实际压装曲线的发展趋势存在一定差异,其原因为以下方面。
1)轮座φ194形位公差差异。实际车轴轮座和车轮毂孔都存在圆柱度、直线度,且车轴轮座存在相对于轴线的圆跳动,轮座经过滚压强化;除圆柱度外,其余形位公差、滚压表面仿真难度较大。
2)车轴和车轮引入部位尺寸误差。车轴、车轮引入部位因实际加工会引起角度和长度差异,测量存在一定难度,该差异导致压装曲线初始状态各不相同。有限元仿真建模采用公称尺寸建模,仿真过程中引入部位的尺寸相同。
3)轮对压装水平因素影响。实际压装过程中,轮对压装前车轴须进行水平调整,减少水平精度影响,确保车轴中心线与压头中心线平行;车轮在压装前套至轮座引入部,而且要对正压紧;轮对压装后测量并调整左右轮位差,以及内侧面的3处轮对内侧距之差。有限元仿真模型一般按中心线完全重合进行建模。
3 压装影响因素敏感性分析
正交试验设计通常是利用已有正交表科学地安排和分析多因素试验的一种方法,利用正交表合理安排试验,通过少量试验进行分析,采用直观分析法分析各因素的影响大小,进而推断出最优试验条件或生产工艺[16-18]。文中利用正交试验设计分别对过盈量、车轴轮座圆柱度及车轮毂孔圆柱度、冷压过程摩擦系数进行组合,依据相关图纸和生产实际确定了4个主要影响因素,并各按3个水平计算所选择参数[19-21]。建立注油压装和冷压2种有限元分析模型,分析4种影响因素对压装曲线最大压入力、起点陡升压力的影响,进行理论影响因素敏感性分析[22]。分析压装参数范围:过盈量0.19~0.21 mm、车轴轮座圆柱度0.005~0.025 mm、车轮毂孔圆柱度0.005 0~0.020 0 mm及冷压过程摩擦系数0.11~0.15。
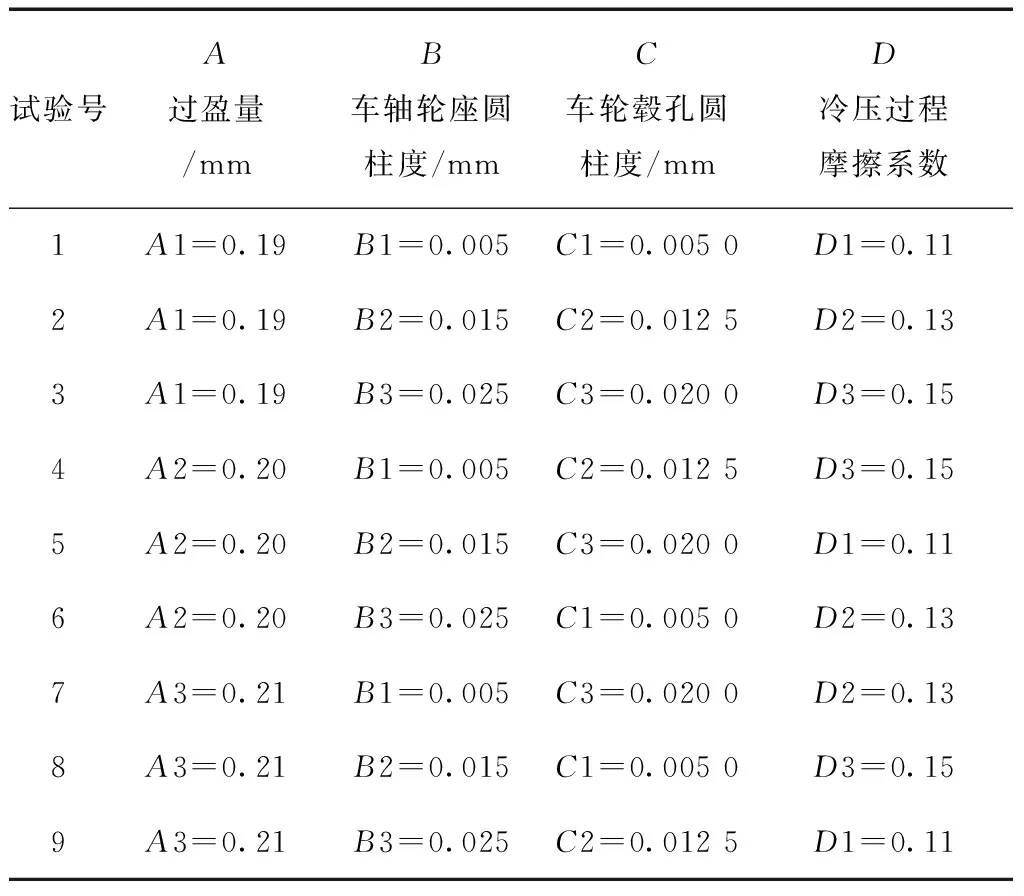
表3 压装曲线参数正交表L9(34)
为保证基础模型的一致性,除了140 MPa注油压力和注入高压油后摩擦系数外,轮对注油压装模型、冷压模型完全一致。根据有限元仿真结果,计算平均值及极差,分析不同结果下的参数敏感性。结果如表4所示,可得以下结果。
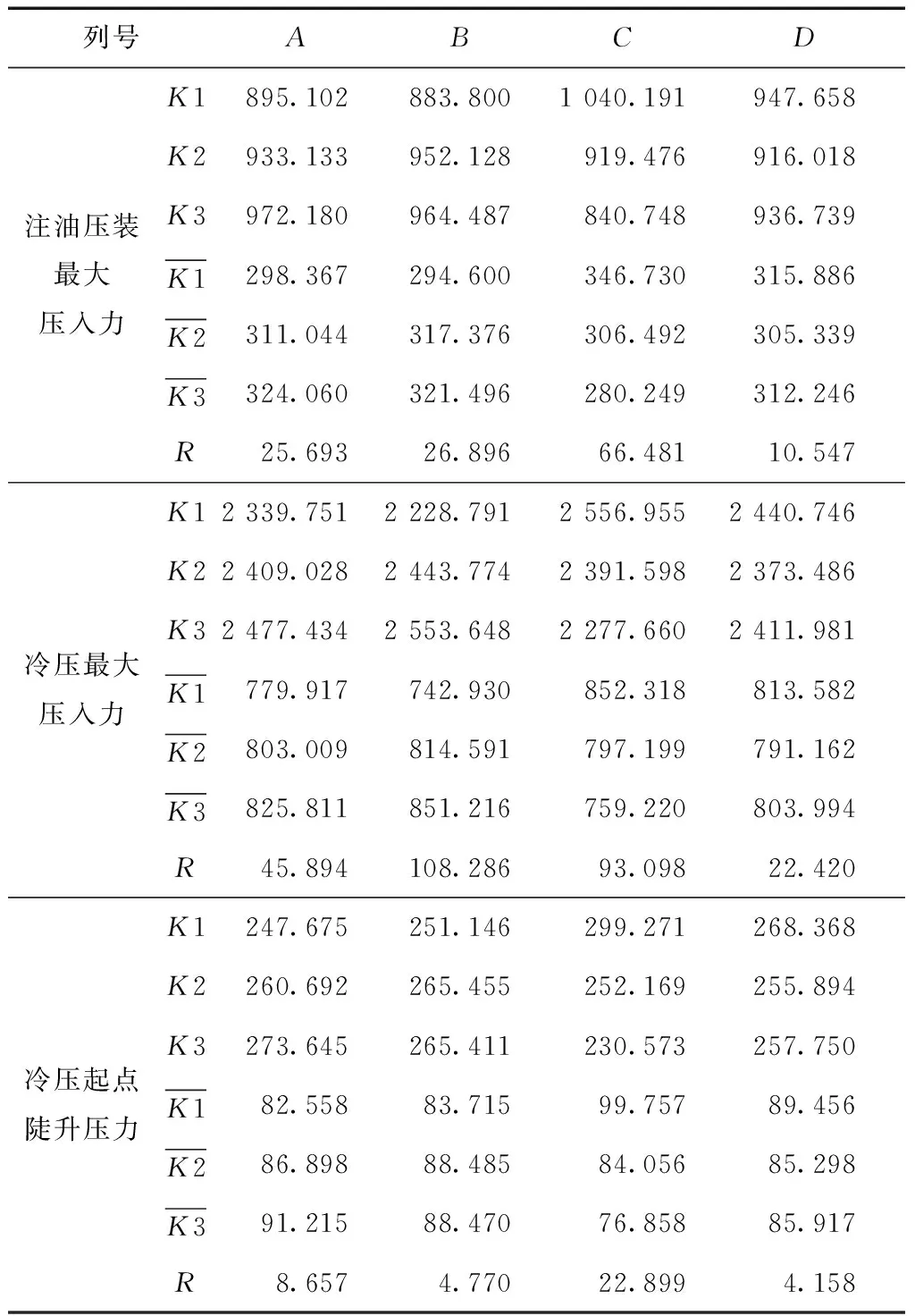
表4 参数敏感性分析
1)轮对注油压装中,影响压装曲线中注油压装最大压入力的参数敏感性由高至低依次为车轮毂孔圆柱度、车轴轮座圆柱度、过盈量及摩擦系数。
2)轮对冷压中,影响压装曲线中冷压最大压入力的参数敏感性由高至低依次为车轴轮座圆柱度、车轮毂孔圆柱度、过盈量及摩擦系数。
3)轮对冷压中,影响压装曲线中冷压起点陡升压力的参数敏感性由高至低依次为车轮毂孔圆柱度、过盈量、车轴轮座圆柱度及摩擦系数。
4 结 论
车轮及车轴压装是转向架制造的关键零部件,对铁路车辆运行安全意义重大。根据正交分析法对压装影响因素进行敏感性分析,得出以下结论:
1)对轮对注油压装进行仿真,发现仿真结果与真实结果接近,且误差小于5%,因此,仿真结果与理论计算结果基本一致;
2)注油压装过程中,对压装力的影响因素依次为车轮毂孔圆柱度、车轴轮座圆柱度、过盈量及摩擦系数;
3)冷压过程中,对压装力影响因素依次为车轴轮座圆柱度、车轮毂孔圆柱度、过盈量及摩擦系数;
4)冷压过程中,对起点陡升压力影响因素依次为车轮毂孔圆柱度、过盈量、车轴轮座圆柱度及摩擦系数。
