数学模型在公路造价控制中的应用综述

2021-09-16赵晓薇马婷婷陈宝光帖卉霞

交通科技与经济 2021年5期

汪优，赵晓薇，马婷婷，陈宝光,2，帖卉霞

(1.中南大学土木工程学院，湖南长沙 410075；2.北京中交京纬公路造价技术有限公司，北京 100025；3.交通运输部路网监测与应急处置中心，北京 100088)

在公路工程施工阶段，由于施工方案及人、材、机等多因素影响，工程项目实施期间概预算超前期估算、施工图预算超概预算现象普遍存在。目前，公路工程造价普遍采取定额计价方式，因此，要想有效控制公路工程造价、追溯源头，需要通过合理科学的手段计算出符合当前经济水平的定额值。

“定额”是指在一定的生产力水平和科学技术水平情况下，生产条件正常，施工组织合理，且能够合理使用材料和机械的情况下，完成单位合格产品所必需消耗的人工、材料、机械设备和资金的数量标准[1-2]。定额编制工作是将现场测定、经验估计或典型案例获取的原始数据进行归纳总结，针对不同条件和情况，运用不用的数据获取方法采集比较准确的数据，对这些数据进行分析和挖掘，从而确定合理的数值和标准。

从公路工程定额体系的建立看，无论是定额编制方法、定额管理等都较以往取得了较大进步，但仍然存在定额编制方法不够科学、定额水平不能够反映真实的生产技术能力情况。如果对现场或以往数据的处理方法简单，如直接采用平均数值等方法，很容易导致得到的数值与实际情况不相符。随着新技术、新工艺、新材料及新机械的不断出现，在对此类“四新”项目测定时由于收集到的数据较少，且没有历史数据可参考，因此，对于这类贫样本、少样本情况往往需要结合数学模型对定额进行科学预测。

针对上述情况，通过纵向、横向2个维度对以往文献进行梳理总结。纵向上，以时间顺序为纵轴，梳理数学模型在我国定额编制工作中的发展历程；横向上，以数学模型的适用情况为横轴，对数学模型进行分类，梳理不同的数学模型在我国定额编制工作中的实际应用范围。通过总结和梳理，分析当前公路工程预算编制中常用的数学模型及其适用情况，明确未来的研究方向，以期为公路行业造价人员的定额编制、测算、研究工作提供参考，从而达到控制公路造价的目的。

1 我国公路工程定额编制现状

我国的公路工程定额编制一般可分为4个阶段：前期准备阶段、数据收集阶段、数据处理阶段和后期测算阶段，如图1所示。为保证定额的科学性、准确性、全面性，学者们在数据处理阶段采用了数学模型方法，通过更加科学的方法，准确、全面地求得定额数据，使其结果更具理论性、科学性和实践性。

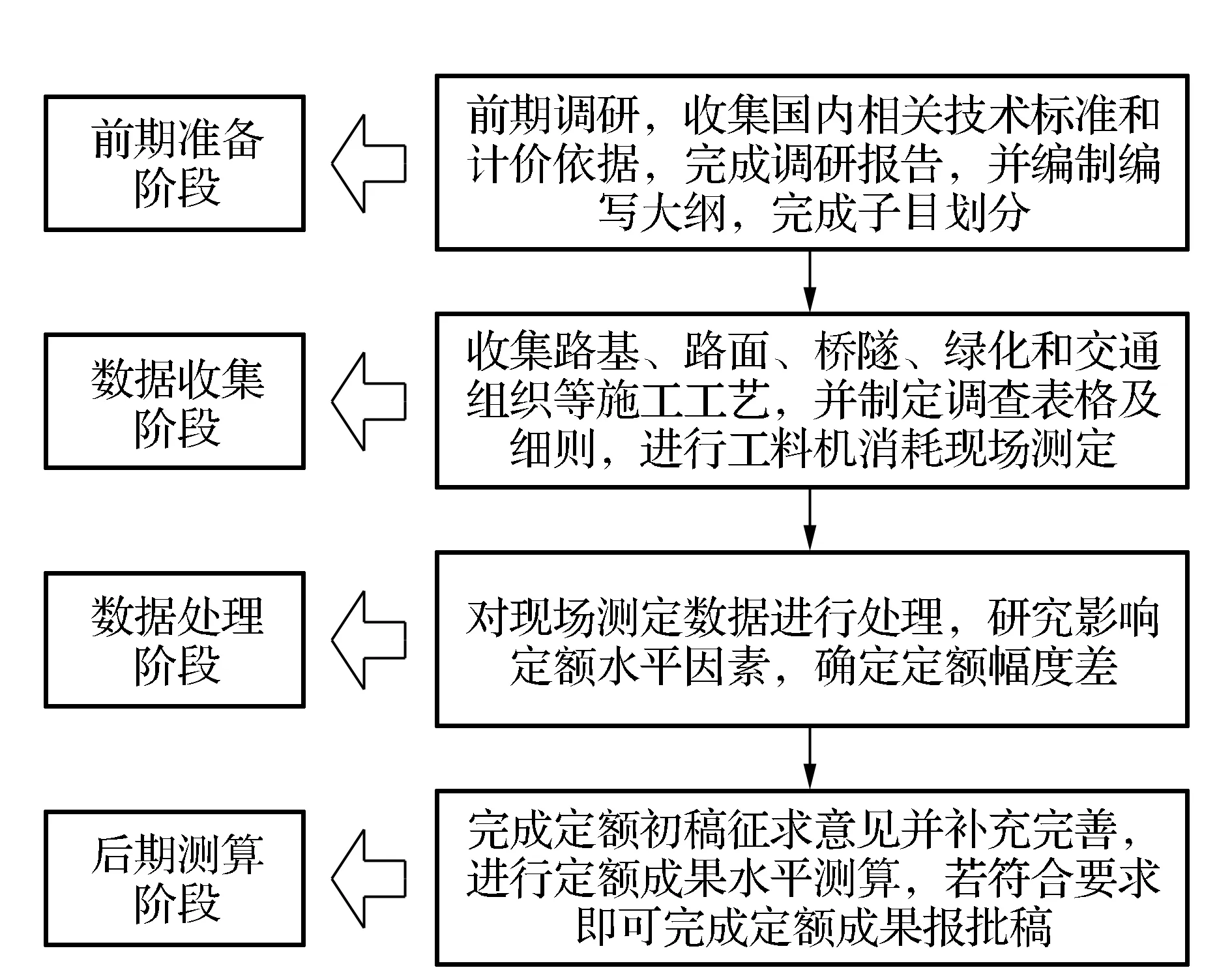
图1 公路工程定额编制一般流程

在数据处理阶段常采用的方法有经验估计法、统计分析法、技术测定法、类推比较法等4种[3]。在实际应用中，4种方法都存在各自特定的应用条件、适用范围及局限性，应根据实际情况综合使用。以科学准确的技术测定法数据为支撑，采用统计分析法对数据进行整理分析，运用经验估计法和类推比较法对实测值进行验算，综合确定最终定额[4]。

现有公路工程定额体系仍然较为传统，是以对定额等的计价依据编制及审查为重点，但通过该定额体系计算出来的造价往往与市场造价存在偏差。国际上大多采用“工程量清单+市场单价”的定额模式，以市场价格信息作为着重点。我国建筑市场大量采用的也是工程量清单计价方式，该计价方式有益于造价控制，我国交通行业也开始着手实现在招投标领域由定额计价向工程量清单计价逐步转型。[5-7]

2 数学模型在定额编制工作中的发展历程

随着我国公路工程行业的发展，学者们对如何科学编制定额这一问题的研究也越来越深入。总体看，数学模型在我国定额编制中的发展经历了以下3个阶段：简单数学模型发展阶段，复杂数学模型发展阶段，复合数学模型发展阶段。如图2所示。

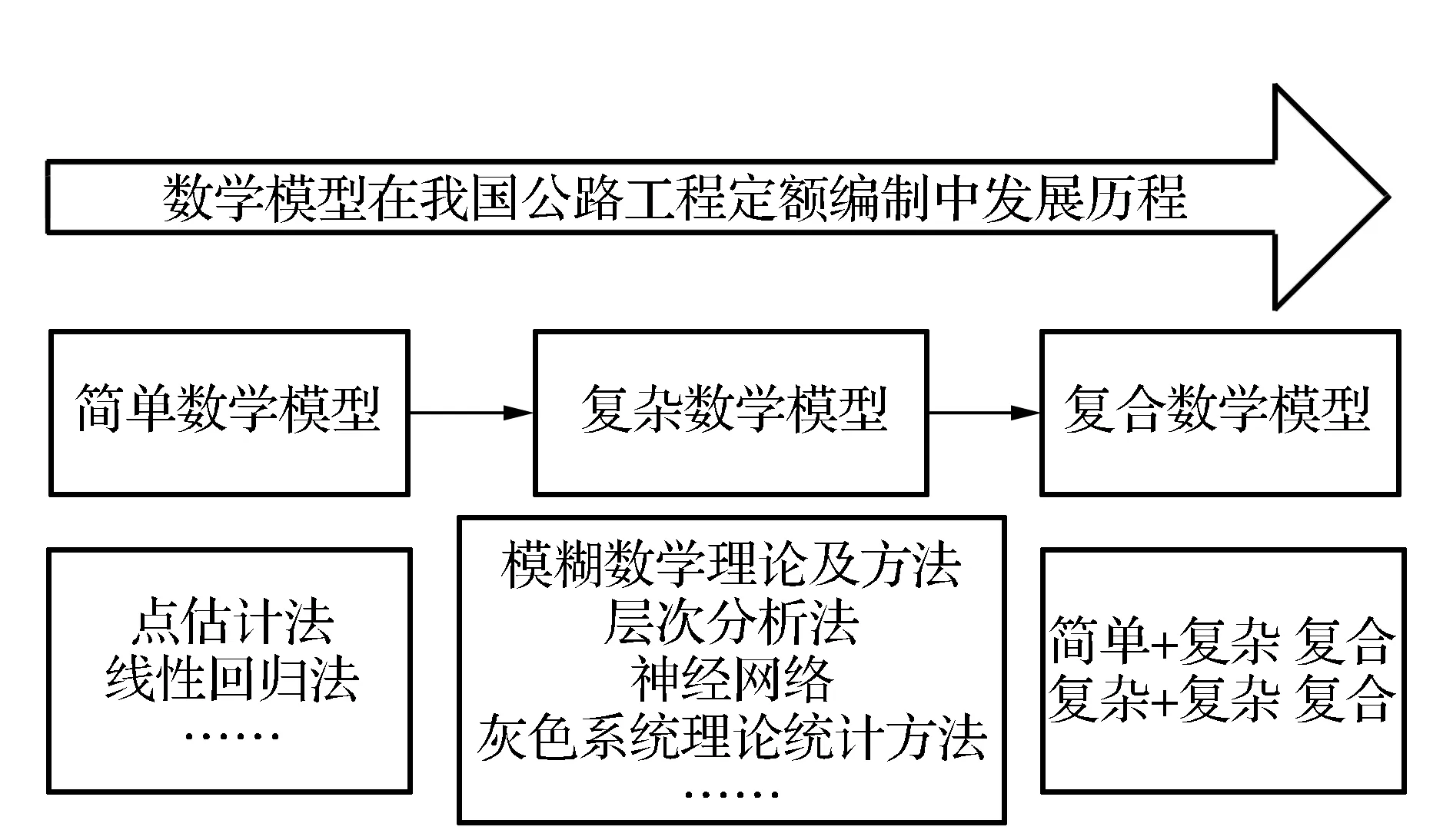
图2 数学模型在我国定额编制工作中发展历程

简单数学模型指的是容易掌握、运算简单，且运用起来较容易理解的数学模型；复杂数学模型是指运用较为复杂，需要一定的知识储备才能合理运用的数学模型；复合数学模型是指将2种或2种以上数学模型共同使用，以得到更加合理数值的数学模型，如模糊层次分析法即为模糊数学法和层次分析法复合后的模型。

2.1 单一简单数学模型

在单一简单数学模型阶段，不同科学家提出了在公路工程预算编制中运用不同的基础数学模型，该阶段采用的主要数学模型有点估计法、线性回归法等。该类模型使用较简单、较容易被理解，是最早用于定额计算的数学模型，但由于其准确性较低，因此目前基本不单独采用该类方法，而是将其和其他数学模型复合起来使用，以提高数据精度。

杨赞峰等[8]提出采用点估计法，用测样平均数和测样方差估计总体参数，通过施工现场测定或统计出的一组数据，由局部到总体得到定额总体情况。张世松[9]将线性回归模型应用于公路小修定额编制中，通过“原料资料工料机消耗-原始资料计算的分析基价-定额子目的工料机消耗”的分析过程，求得定额。王首绪等[10]采用一元线性回归法，利用因变量与自变量之间的强关联性，通过已有条件下的定额数据，推算出特定情况下的定额消耗量。

2.2 单一复杂数学模型

随着定额编制要求的提高及统计学的不断发展，人们逐渐采用更加科学、复杂的数学模型替代简单模型，对定额进行计算，以期获得更为准确、科学的定额。在该阶段积极探索数学模型在定额编制中的应用，具体采用的数学模型包括模糊数学理论、层次分析法、灰色系统模型、神经网络及蒙特卡洛法等。

2.2.1 模糊数学理论及发展

模糊数学是研究和处理模糊性现象的一种数学理论和方法，又称Fuzzy数学。王首绪等[11]于2002年借助模糊数学理论，在政府规定和市场竞争的矛盾中，总结得出模糊类比法，以评估造价的合理性。具体步骤包括：收集同类工程资料进行分析，以数据相关程度选取类似工程，在数据估价阶段划分比较项目，进行因素比较和修正计算，对修正结果进行再调，最后确定造价。毛红日等[12]提出采用模糊物元方法，对待评价方案构建指标体系的模糊物元模型，并通过AHP法确定各指标权重，计算最终优度，客观地评价各测定方法的优劣，从而选择子目的最优测定方法。

2.2.2 层次分析法及发展

层次分析法(Analytic Hierarchy Process)，是由美国运筹学家T.L.Saaty提出的一种多指标定量综合评估方法，通过同一层次中各评估指标的初始权重将定性因素定量化，使得各影响因素条理化、层次化，减少主观因素影响，使评估更加科学。

樊胜军[13]于2002年首次提出将层次分析法(AHP)应用于工程评标，以模糊数学、管理学、运筹学、管理运筹学理论为基础，提出了建设工程评标定标的层次分析法模型。王首绪等[14]应用层次分析法计算定额幅度差，根据专家打分对公路工程各影响因素进行量化，更科学地建立各影响因素权重，避免确定权重时的主观片面性。

邵宏[15]于2002年首次将模糊层次分析法(FAHP)应用于公路工程造价研究，将FAHP法与价值工程理论相结合，提出对不同设计方案进行必选，从而选出最优方案。王首绪等[16]在AHP法、FAHP法的基础上，采用改进层次分析法(IAHP)对判断标度进行简化，由九标度法简化为三标度法，解决了传统层次分析法计算过程和数据处理都较为复杂的问题，减少了评价过程中的主观因素，使评论结果更客观地反映实际。刘颖[17]将AHP法和熵权法相结合，通过双重权重计算，对AHP法计算得到的权重进行修正，进一步提高了数据的可行性及客观性。

2.2.3 神经网络及发展

神经网络具有较好的非线性处理能力，在模式识别、信号处理、判释决策、组合优化、知识工程等领域具有特别优势。

李茂英等[18]于2002年将BP神经网络应用于公路工程造价预测，在12个公路工程实例的基础上，10个用于学习训练，2个用于模拟验证，结果表明应用BP神经网络来预测公路工程造价可行且有效。王敬群[19]利用人工神经网络建立公路工程路基的投资估算模型，并与其他估算模型比较，结果表明神经网络模型效果优于其他估算模型，对公路建设项目的投资决策有重要指导意义。

2.2.4 灰色系统理论及发展

灰色系统理论，是我国学者邓聚龙教授1982年创立的一门新兴学科，以“部分信息已知、部分信息未知”的“小样本、贫信息”不确定性系统为研究对象，通过对已知信息的生成、开发，进而提取得到有效信息，从而实现对运作行为和演化规律的正确把握和描述[20]。灰色系统理论主要包括灰色关联分析、灰色预测模型等，其在公路造价的发展中都起到了重要作用。

郭颖[21]将灰色预测应用于公路工程造价控制研究，通过灰色预测模型，即GM(1，1)模型，对历史数据序列进行提取，从而预测未来的价格风险。通过灰色预测和回归分析、指数平滑等其他预测方法比较，发现灰色预测模型的预测结果更好，更符合公路项目建设过程中的价格多变特点。

灰色关联分析最初多用于公路工程建设方案的优选及工程质量判定等研究，之后也逐渐用于定额编制。李强[22]将灰色关联理论引入到高速公路改扩建造价控制中，通过造价对比分析各影响因素之间的关联度，从而建立基于灰色关联分析理论的造价控制影响因素分析模型。曹洁梅[23]则将灰色理论与欧氏距离理论相结合，采用灰色关联度确定各项指标权重，并根据欧氏距离理论选取待估算工程的相似工程，以相似工程作为样本提高估算的准确度。

2.2.5 蒙特卡洛法及发展

蒙特卡洛法又称随机模拟法或统计实验法，由S.M.乌拉姆和J.F.诺伊曼首先提出，其基本原理是利用概率论中的大数定律，即中心极限定理，求出某事件的概率，或某个随机变量的平均值，以此作为问题的解，具有简单灵活、收敛速度与问题维数无关等优点。

在定额编制中，蒙特卡洛模拟可将少量样本数据进行模拟，产生大量数据，解决样本数据不足问题。唐秀丽[24]以已有的工程造价数据库为定额编制依据，利用蒙特卡洛模拟方法快速编制企业定额。王卓[25]针对高速公路改扩建工程中数据采取不足的特点，以现场实测的少样本为基础，通过蒙特卡洛模拟模型，结合幅度差系数，确定改扩建预算的定额消耗量。

2.3 复合数学模型

随着定额编制的不断发展，单一数学模型已不能再满足现阶段要求，科学家们开始尝试将不同的数学理论及数学模型相结合，将复合数学模型的形式应用于定额研究，以进一步提高测算结果的科学性及客观性。复合数学模型有以下2种组合方式：简单数学模型+复杂数学模型；复杂数学模型+复杂数学模型。

2.3.1 简单数学模型+复杂数学模型

赵学明[26]将一元回归分析与灰色预测模型GM(1，1)进行复合，以6个同类工程项目为研究对象，分别借助SPSS软件计算回归分析预测成本，并借助MATLAB软件计算灰色预测模型的预测成本，最终取2种结果的平均值以减小误差。

2.3.2 复杂数学模型+复杂数学模型

在定额编制过程中，通常会出现2种复杂数学模型复合使用的情况，不同的方法在定额编制过程中往往发挥不同作用，2种模型的复合使用，使得定额更加准确科学。

1)模糊数学理论+X数学模型。在该类复合数学模型中，“模糊数学理论+X数学模型”是最常见的复合使用方式。模糊数学理论和层次分析法结合使用，并复合为模糊层次分析法(FAHP)，解决了层次分析法中检验判断矩阵是否一致的困难问题。杨玉胜等[27]将FAHP法应用于高速公路改扩建工程预算定额，根据改扩建工程与新建工程的差异，建立预算定额消耗量对比估算系数的参差结构，将估计指标量化获得对比估算指标，对比获得改扩建工程定额。

李驰宇[28]于2006年将模糊理论与BP神经网络结合使用，以预测造价。首先，通过模糊数学对收集的公路造价数据进行筛选，获得与预估工程近似的工程资料作为训练样本，再采用较成熟的神经网络BP算法，通过3层前馈神经网络实现高速公路工程特性与工程造价之间的复杂非线性映射，以收集到的造价资料为基础，预测指定高速公路的造价值。

2)X数学模型+Y数学模型。以往研究中也经常出现将2种不同类型的数学模型结合使用情况，不同的数学模型能起到不同作用，以达到最终目的。郑秀珍[29]在公路工程施工定额编制研究中，将改进层次分析法(IAHP)与灰色聚类分析法结合使用，构建了基于IAHP的灰色聚类公路工程施工定额计算模型。其中，层次分析法用来确定聚类对象权重，并根据权重通过灰色聚类法对各聚类对象进行分类，以获得不同灰度下的定额结果，进行修正后得到最终定额。

袁新杰[30]在公路补充定额编制方法研究中，将层次分析法(AHP)与BP神经网络复合使用。通过AHP法对影响因素进行权重分析，获得5个最主要的影响因素，将其作为神经网络的输入层。通过BP神经网络对已有定额数据进行模拟，并对定额生成系数进行预测，获得最终定额。

2.4 综合评述

以数学模型在公路工程定额编制中的发展历程为轴线，梳理了发展历程中的3个不同阶段。在最初阶段，绝大多数定额测定采用经验估计法或统计分析法，或是通过现场测定和收集的原始数据及资料进行平均数值数据处理方法，得到的造价数值往往简单，不能真实地反映生产技术能力情况。因此，2001年开始，人们逐渐采用更科学的数学方法来提高数据的精确度，如简单的点估计法、线性回归法等。随着行业内新技术、新设备的不断出现，加上人、材、机等因素限制，一些需要测定的工序无法获取较多样本，对于这类贫样本、少样本情况，人们逐渐尝试采用统计学中的模糊数学理论、灰色关联分析等模型，随着计算机及智能化的发展和普及，又进一步发展使用与计算机结合更加紧密的神经网络、蒙特卡洛模拟等模型。经过近10多年的研究和验证，这些方法均已较广泛地应用于定额编制中，并拥有各自的适用情况。

3 数学模型分类及适用情况

通过对定额编制过程中使用的数学模型进行分析可知，根据使用时基本原理的不同，定额中常使用的数学模型可分为3类：数据处理类；关联分析类；权重分析类。其中关联分析类和权重分析类在一定情况下可通用。如图3所示。

图3 定额编制中常用到的3类数学模型

3.1 数据处理类数学模型

数据处理类方法的基本原理是针对某一特定项目根据其获得的已有数据进行分析，得到拟得数据。具体地，根据数据样本数量又可分为多样本数据处理和贫样本数据处理2类。

多样本数据处理常采用最简单的数据处理方法，如线性回归法、点估计法等。但在公路工程建设过程中，原始数据往往具有少样本特点，因此需要采用更科学的方法，如灰色预测模型、神经网络或蒙特卡洛方法。对已有数据进行训练，采用小样本、贫样本较好，训练能得到大量数据，最终取均值获得定额，该类数学方法应用在定额中可实现以下2个功能。

1)通过对施工现场实测到的数据进行分析，得到最终定额。文献[25]中王卓借助蒙特卡洛模型，通过50个现场实测数据，分别模拟得到1 000个、5 000个、10 000个数据，精度判断后，取模拟得到的10 000个数据均值作为最终定额；王兆强等[31]针对水泥-砂砾石坝施工，结合真实数据运用蒙特卡洛进行模拟，解决了建设初期由于缺乏样本数据和代表性工程而导致的精度结果不高问题。

2)通过往年、现有的大量造价数据，预测未来的造价数据，刘颖等[32]采用灰色预测模型GM(1，1)，基于2008—2014年高速公路四车道改八车道的平均造价，预测得到2015—2017年的造价数据。

3.2 关联分析类数学模型

关联分析类数学方法的基本原理是分析不同对象之间的隶属度，判断他们之间的相似度和关联度。现阶段，定额编制中常采用的方法有模糊类比分析、灰色关联度分析等，虽然这些方法的具体实现过程有差别，但本质上都符合上述原理。在定额中，根据对象和想要实现目标之间的关系主要实现以下功能。

对相似工程、相似数据进行横向比较，对不同项目、不同数据之间进行关联度、相似度比较，选取精度最高、最相似的项目和数据，并选取一定的幅度差范围进行调整，最终得到定额。如龙琰[33]运用模糊数学中的模糊贴近度和灰色系统理论中的灰色关联度，通过自然条件、工作对象、交通干扰状况、工人掌握状况4个因素，计算5个样本地区与整个地区的综合相似度，最后选取相似度大的样本代表值确定最终定额。刘燕[34]等运用区间模糊推理方法，通过施工对象、技术方法、作业环境3个影响因素，判断拟编制定额与相似定额之间的相似度，求出两者之间的综合相似程度

3.3 权重分析类数学模型

权重分析类数学方法的基本原理是将定性分析转化为定量分析，通过专家打分法、德尔菲法等方法收集数据，得到各因素权重，最终确定最优的一个或多个因素。定额中主要涉及的方法有层次分析法及其衍生方法(模糊层次分析法、改进层次分析法)、主成分分析法等。数学方法常用来选取最优方案，在定额中可实现以下功能。

1)在众多影响因素中确定主要影响因素。先通过经验选取众多影响因素，再经过初步筛选后获得10～14个备选因素，通过专家打分或德尔菲法，求得各指标权重，将权重由大到小排序，取前5个指标作为二次筛选后的最终影响因素。

2)权重分析在一定的情况下同样可实现关联分析。如在改扩建工程定额编制中，专家分别针对各影响因素对新建工程、改扩建工程的重要性进行打分，进行两两因素比较后再构建判断矩阵，计算权重并进行一致性检验，最终确定新建工程与改扩建工程之间预算定额消耗量的对比系数，通过新建工程定额对比系数获得改扩建工程定额。

3.4 综合评述

总结了3种不同类型的数据模型，不同的数据模型在定额编制中发挥不同功能。在实际应用中往往会结合2种或多种方法使用，以提高定额精度或实现不同目的，主要包括以下结合方式。

1)运用2种相同类型的方法对同一数据进行处理。同时利用模糊贴进度和灰色关联度概念来计算不同项目之间的贴进度/关联度，以获得不同项目之间的综合相似度，采用相似度最大项目的代表值来确定定额。

2)运用2种不同类型的方法对不用类型的数据进行处理。如在高速公路改扩建工程定额编制过程中，定额编制往往有2种情况：一是针对新建工程中没有的、改扩建工程中独有的子目，通常通过现场测定后，采用贫样本数据处理类的数学模型训练后得到；二是针对新建工程和改扩建工程中均存在的定额子目，由于施工环境、施工组织等因素的影响往往会导致改扩建工程功效较低，因此，需要对两者进行权重分析，得到其中的对比系数，经调整后确定。