基于培养学生自主探索能力的复习课教学

颜容

[摘  要] 文章分析了当前复习课中存在的一些常见问题，并以一节折纸课为例，通过课堂实例的开展，谈谈如何在复习课中培养学生的自主探索能力，以提高复习效率与学生的数学核心素养.

[关键词] 自主探索;复习课;折纸

新课标明确提出：通过学习，要让学生初步掌握一定的实际能力与创新精神[1]. 其中，培养学生的自主探索能力是实现这一任务的重要方法之一. 长期以来，复习课的教学基本以知识点的罗列和解题训练等方式为主，这种千篇一律的教学方法在一定程度上束缚了师生的手脚，难以发挥学生的主观能动性，很难实现新课标所倡导的教育理念. 为此，笔者以一堂复习课教学为例，具体谈谈如何培养学生的自主探索能力，实现学生实际操作能力与创新能力的发展.

现状分析

复习课具有帮助学生深度理解知识、规范解题过程、查漏补缺与优化解题方法等作用. 在新课标引领下的复习课中培养学生的自主探索能力是学生能力发展的需求，也是时代发展的需求. 但是，在當前的复习课教学实践中，笔者发现存在着以下几种问题.

1. 功能定位不明确

目标是每节课的方向，若复习目标模糊不清，则会出现教学偏离轨道的尴尬局面. 一些教师将复习课误上成习题训练课，一味地就题讲题，而不去提炼教学方法，更不思考如何让学生在复习课中发挥自主性，缺乏知识与方法提炼的过程.

2. 内容组织不合理

所谓的复习课，是在学生已有知识的基础上进行查漏补缺、融会贯通的课堂. 有些教师却硬生生地将复习课上成了新课，只针对一两个知识点进行授课;也有些教师就是将原有的基础知识简单地再现一次，使得学有余力的学生出现“吃不饱”的现象.

3. 学生积极性不高

实践中，我们常发现教师在课堂上讲得唾沫横飞，而学生却处于昏昏欲睡的状态. 究其主要原因还在于教师没有意识到教学的主体应该是学生，教师只有转变观念，鼓励学生积极参与到教学活动中来，才能让学生化被动学习为主动学习. 尤其是一些学优生，认为自己的知识储备已经达标，故而出现对复习课积极性不高的现象.

课堂实例

想在复习课上培养学生自主探索的能力，可以当前复习课教学中存在的问题为出发点，通过教师教学理念的转变，充分发挥每个学生的主观能动性，鼓励学生在积极参与中实现共同成长[2]. 主要可将教师的教，转变为学生的思;教师的讲，转变为学生的说;教师的动，转变为学生的操作. 故此，笔者以一堂复习课为例谈谈具体的操作方法.

1. 小试牛刀

课前通知学生准备一些矩形的纸片、直尺、量角器、剪刀等常规用品.

师：本节课以动手操作的方式来复习一些与对折有关的知识（学生跃跃欲试，充满期待）. 请大家思考一下，假如让你折叠手中的一张矩形纸，你能得到一些什么图形？动手尝试折一折.

（学生操作）

生1：我折出了简单的角平分线、线段的垂直平分线.

师：哦？说说你的折叠方法.

生1：假设线段AB为矩形的一条边，将线段对折，使得点A与点B重合，线段AB的垂直平分线即这条折痕;对折矩形中的一个角，让这个角的一条边与另一条边重合，此时中间的那条折痕即该角的角平分线.

师：这两种图形具备怎样的特征？

生1：这两种图形都是轴对称图形.

2. 渐入佳境

师：非常好！我们还可以折出什么图形？

生2：我折叠出了正方形. 如图1所示，折叠矩形ABCD中的∠ADC，获得角平分线DF，以F点为折叠点，使得线段FB与线段FA重合，点B落在线段FA上，此时得到的四边形AFED即一个正方形.

师：这是我们折纸中常用的一种方法，通过这种折叠方式能快速得出正方形这个特殊的四边形. 除此之外，我们还能用怎样的折叠方式得到其他特殊的四边形呢？

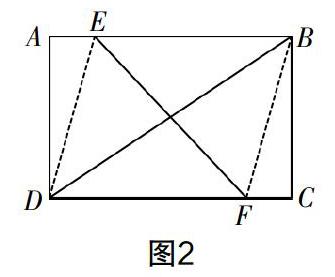
生3：还可以折叠出菱形. 如图2所示，沿对角线折叠矩形ABCD，得出折痕BD，再对折线段BD，获得折痕EF，再以BF，ED为折痕进行折叠，所获得的四边形EBFC为一个菱形.

师：哦？为什么说四边形EBFD是一个菱形？这个折叠过程用到了哪些知识点？

生4：矩形为中心对称图形，容易证得四边形EBFD为平行四边形，因这个四边形中的两条对角线互为垂直的关系，可得四边形EBFD为一个菱形. 这里面涉及了轴对称、中心对称及菱形的性质等知识.

3. 开拓思维

师：非常好！把涉及的知识点都说到了. 有没有同学能折叠出正三角形？

生5：如图3所示，先将矩形沿MN进行对折，再将矩形沿着AE对折，使得B点落在线段MN上，记为点G，最后沿着EG折叠，获得的△EAF就是一个正三角形.

师：这个方法不错，你是怎么想到的？

生5：我是根据等腰三角形中若有一个角为60°，那么这个三角形就是正三角形这一判定方法想出来的.

师：不错！请各位同学将这种折纸方式的证明过程写下来.

（证明过程略）

生6：我折叠出了一个正六边形.

师：是吗？说说你怎么折出来的呢.

生6：如图4所示，①先将矩形ABFE的AB边与EF边重叠对折，CD为折痕;②折叠出正三角形DM′J，将AB边与DC边重合对折，与正三角形DM′J相交于点P和点A′;③用相同的方式折叠四边形DCFE，最后展开，则获得正六边形DPA′JGQ.

师：听起来很不错，你能说说六边形DPA′JGQ是正六边形的理由吗？

生6：证明△DM′J为正三角形的方式与上面的证明方法一样，在此基础上继续证明各条边和各个角是相等的，则可证明此图形为正六边形.

4. 举一反三

师：太棒了！这位同学的思维方式值得我们借鉴，大家还能折叠出更多的特殊图形吗？

生7：还能折叠出黄金矩形.

师：说说你的想法.？摇

生7：我是通过折叠先找到了黄金分割点，再根据这个点获得黄金矩形.

师：有创意，具体的折叠方式是怎样的？（同学们也充满期待）

生7：如图5所示，①先将矩形折叠，截取出一个正方形ABCD，通过折叠找出BC的中点E，折叠出线段AE，在折痕AE的基础上，通过折叠让线段BE与线段AE重叠，点B落到AE上记作点B′;②同样的折叠方式，在线段AB上找到点B″，可得AB′=AB″，如此可得点B″是线段AB的黄金分割点;③以B″点为折叠点，让线段BB″与B″A重合，在CD上的折叠点为C′，如此折叠后的矩形DC′B″A为一个黄金矩形. （证明过程略）

师：非常好，看来同学们对折纸的研究越来越深入了.

接下来又有同学提出折叠正八边形、黄金三角形等特殊图形的方法，整个课堂充满探索味儿，学生一个个都跃跃欲试，总希望自己能折叠出比别人更厉害的图形.

教学思考

复习课与新课最大的区别在于系统性与整体性，对于各种特殊图形的性质，教师若一个个地进行讲解复习，让学生进行解题训练，难免会产生枯燥感[3]. 笔者选择了操作性活动的方式让学生自主探索，充满乐趣的同时，还能有效地深化学生对各个图形性质的理解与掌握.

随着新课改的深入，动手操作实践成了热门话题，学生在动手操作中充分发挥想象，通过观察、分析、推理等方式自主探索问题的解决办法. 因此，动手操作既能深化学生对知识的掌握，又能考查学生的实践能力. 本节课涉及的特殊图形比较多，学生在折纸过程中结合每种图形的性质与判定方法，反推出图形的折叠步骤，折叠完毕再书写证明过程，更锻炼了学生对知识的运用能力. 整个过程需学生高度集中注意力，积极思考与探索，才能跟上课堂节奏.

本节课折叠问题中涉及了勾股定理、等腰三角形、角平分线、正三角形、黄金分割、垂直平分线等重点知识. 学生以折纸的方式进行回忆与思考，逐渐理清整个知识的脉络，不仅有效地提高了学生的动手操作能力，更重要的是提高了学生的思维能力与综合素养.

总之，在复习课中引入自主操作探索的教学方法，能起到良好的复习作用，学生在探索中理清知识脉络，更加牢固地构建知识结构. 自主探索的方式可将枯燥的复习课变得更有生机与活力，从真正意义上实现学生思维的自由.

參考文献：

[1]中华人民共和国教育部. 义务教育数学课程标准（2011年版）[S]. 北京：北京师范大学出版社， 2012.

[2]何云英. 准目标  习知识  炼方法  善反思——“相似三角形专题复习”课堂实录与思考[J]. 中学教研（数学）， 2016（09）.

[3]（美）乔治·波利亚.数学的发现（第二卷）[M]. 刘景麟译. 呼和浩特：内蒙古人民出版社，1981.