奇异性弹性场分析的新型超级奇异单元法综述
2021-09-15王从曼平学成王醒醒陈梦成
王从曼,平学成,王醒醒,陈梦成
(1.天津科技大学机械工程学院,天津 300222; 2. 天津市轻工与食品工程机械装备集成设计与在线监控重点实验室,天津 300222; 3. 华东交通大学土木建筑学院,江西 南昌 330013)
应力奇异性经常发生在几何形状不连续的结构中,典型的例子有裂纹、孔洞和夹杂等。 分析奇异性应力场时,只有在简单构型情况下才能获得解析解,对于复杂的情况,通常采用数值方法。 有限元法由于其理论的完备性与强大的通用性成为应用最广泛的数值方法之一。 常规有限元法求解奇异性应力场时精度普遍不高,即使可以通过加密应力奇异点领域网格的方法进一步减少误差,但却又会导致求解效率大大降低。后来研究人员采用应力/位移外插法求解奇异性应力场, 但是越接近裂纹尖端,应力和位移的计算值与实际理论值误差越大,导致应力/位移外插法无法得到高精度的结果。为了提高精度,Nisitani 等[1-2]和Ping 等[3]采用奇异点应力法计算缺陷尖端奇异性应力场,这种方法虽然计算精度较高, 但在求解时需要先给定一个参考问题的精确解,然后利用待求问题和参考问题的应力比值来求解奇异性应力场,限制了此方法的使用。 在对具有双材料界面的界面边进行建模时,Chen 等[4]开发了一种富集元,可以解释仅受机械载荷影响的双材料界面裂纹尖端处的应力奇异性。 与Chen 的工作类似,Gadi 等[5],Pageau 等[6-7]也采用富集有限元来求解奇异性应力场,解释了不同材料连接处的奇异性应力行为,但这种方法仍依赖于单元尺寸。 为了克服常规有限元的缺点,研究人员提出了一系列专门用来处理缺陷尖端应力奇异性的特殊单元,这类单元通常被称为奇异单元。 通过在缺陷尖端使用这类奇异单元,可以对那些含有几何不连续部位的应力场进行有效的数值分析。
在分析二维平面奇异性应力场时,最早使用的裂纹尖端奇异单元是Benzley 型单元[8]和Barsoum型单元[9],其中Barsoum 型单元就是如今使用广泛的四分之一点奇异单元。 Abdelaziz 等[10]提出了一种改进的四分之一点奇异单元,用于对裂纹尖端的奇异点进行建模。 Liu[11]提出了基于边缘的平滑有限元,Jiang 等[12]在他们的基础上开发了一个7 节点奇异单元, 用来模拟裂纹尖端周围的奇异性应力行为。这些单元通常是通过简单地改变标准单元的节点位置来开发的,不需要重新配制,方便实际使用。 其后,Tong 等[13]在杂交元概念的基础上提出了超级混合裂纹尖端奇异单元,将此超级奇异单元与常规有限元结合起来,可以分析平面裂纹尖端奇异性应力场。Lin 等[14]开发了一种混合裂纹尖端奇异单元用于双材料界面分析, 其中混合单元的假定应力和位移场是基于复势技术推导出来的。 Tan 等[15]开发了一种奇异单元来分析在面内热和耦合载荷下双材料楔形体顶点处的奇异性应力场。 扩展Mote[16]和Bradford 等[17]的工作,Madenci 等[18]开发了一 种混合单元,并将其与常规有限元耦合,可以用于分析在机械和均匀热载荷下由材料和几何不连续性引起的奇异性应力行为。Barut 等[19]基于机械和热载荷下的特征函数展开方法,利用应力和位移场的精确解开发了一种奇异单元,用于分析多相材料的奇异性应力场。Zhang 等[20]开发了一种带有弹性夹杂物的n边形奇异单元,用于对具有随机分散夹杂物的异质材料进行力学分析。Cai 等[21]开发了一种用于动态载荷下双材料界面裂纹的新奇异单元。 Li 等[22]基于混合应力函数开发了一种新奇异单元,可以用于各向异性材料中裂纹尖端奇异性应力场分析,且此奇异单元形状和节点的数量可灵活调整。
现有的特殊奇异元大多是针对二维问题,对于三维问题的探究还处于一个不太成熟的阶段。 从二维到三维,除了模型自由度的增多,相当一部分二维假设不再适用,需要重新对其定义。 与平面断裂问题相比, 三维断裂问题的数值分析难度更大,需要解决的问题更多, 但与实际工程应用更接近,具有很大的研究价值。 在三维裂纹的研究方面,目前也有了一定的研究成果。
Kuna 等[23]在混合应力模型的基础上,开发了一种形函数包含裂纹尖端应力的已知奇异行为的特殊裂纹尖端奇异单元, 用来分析三维弹性断裂问题。李翠华[24]构造了一种新的三维奇异单元,可以用于受远场载荷的圆环形和半椭圆形表面裂纹尖端应力场分析,扩展了Ingraffea 等[25]和Banks-skill[26]的工作。 Grummitt 等[27]考虑了用于三维断裂问题的拉格朗日奇异单元的细节,并证明了它的准确性和效率。 Tracey[28]提出了三维奇异单元分析裂纹的几何参数,随后Joao 等[29]使用此奇异单元对一系列断裂力学问题进行建模。 结果表明,在使用正确设计的网格时,分析具有一定的准确性。 Ariza 等[30]提出了一种具有平面几何形状的9 节点二次奇异单元用于3D 断裂力学分析。 陈伟华[31]在三维裂纹的尖端区域采用二维平面和反平面裂纹问题的辛解析本征解作为插值函数,构造出一类三维辛解析奇异单元,将此奇异单元与三维常规有限元相结合可对三维断裂问题进行数值分析。Hu 等[32]提出了一种新辛解析奇异单元用于三维裂纹奇异性应力场分析。
目前为止, 奇异单元已取得广泛发展与应用,但是随着制造和材料技术的不断进步,奇异单元仍存在需要完善之处,例如数值结果仍然依赖于奇异单元的大小;除混合奇异单元外,由于节点处自由度的不同,奇异单元和常规单元之间的单元相容性无法得到满足, 这些奇异单元很难收敛到精确解;多数奇异单元依赖于解析解,通用性不强。 针对这些不足,建立了一系列用于奇异性弹性场分析的新型超级奇异单元。 新型超级奇异单元是基于奇异性位移场和应力场的数值特征解和H-R 变分原理构造的包含缺陷角部的特殊单元,能够用于分析奇异性弹性场。 与其它奇异单元相比,新型超级奇异单元在保证精度和稳定性的基础上,不依赖于单元尺寸,无需任何过渡单元即可与常规单元连接。由于其处理过程是基于数值解建立的,整个问题的实施过程具有很强的通用性,可以应用于任意楔形角和任意材料组合的奇异性弹性场分析。 主要综述了新型超级奇异单元在二维或三维中的裂纹尖端、夹杂角尖端、V 型缺口角尖端、孔洞角尖端、多相材料界面角尖端的应用情况,对新型超级奇异单元的理论推导、单元建立和组装以及分析过程进行了介绍。
1 平面楔形角尖端奇异单元
工程结构中, 如动力系统中转向架焊接接头,由于刚度失配导致应力奇点,是产生裂纹的重要原因之一,奇异场分析对结构组件安全要求有重要作用。工程材料中经常存在V 型孔洞和缺口等非椭圆型微缺陷。 在小应变弹性理论的背景下,这些微缺陷中V 型角尖端引起了奇异应力,继而引起裂纹萌生。 要评价含此类缺陷的疲劳强度,必须准确有效地确定V 型角尖端奇异场。为获得高精度和高效率的奇异弹性场数值解,基于Yamada 等[33]有限元特征法,建立一种新型有限元模型,通过引入陈梦成和Sze 的非协调元[34],得到楔形角部弹性场数值解。
1.1 V 型角尖端奇异单元
如图1 所示为V 型角尖端域。为了得到V 型角尖端奇异弹性场变化函数, 需要依据虚功原理,由特征问题方程来确定特征值和特征向量。 位移形函数采用非协调元, 而材料界面间则满足协调条件。通过位移与应变关系式、Hooke 定理、 材料弹性矩阵,将特征问题方程离散为有限元格式,建立标准特征方程,求解特征值和特征向量[35]。如果求解结果为多特征值,依据Teocaris[36]理论,通过曲线拟合和形函数插值得到的奇异弹性场为

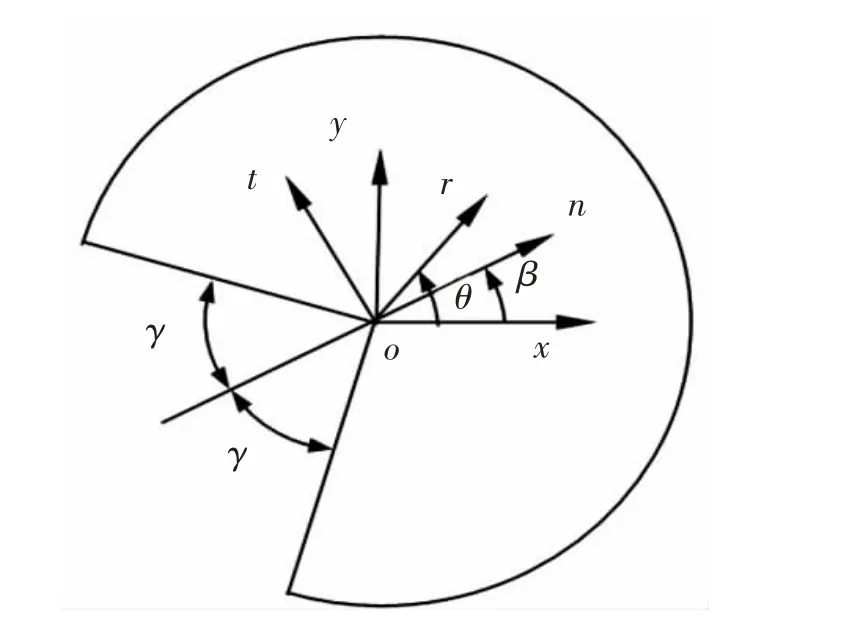
图1 V 型角尖端域及局部坐标系(n,t)Fig.1 V-shaped corner tip domain and the definition of local coordinate system(n,t)
为了准确获得V 型角尖端奇异性应力场,开发了超级V 型角尖端单元[37-38]。 建立新型有限元方法的思想是将原问题图2(a)分解为两个边值问题,如图2(b)和图2(c)所示:①在域Ωc内的混合边界值问题,Γc和Cc为圆周边界条件,该域内应用Pian 和Sumihara[39]开发的4 节点四边形混合应力单元;②在楔形域Ωw内的混合边界值问题,Γw为圆周边界条件。
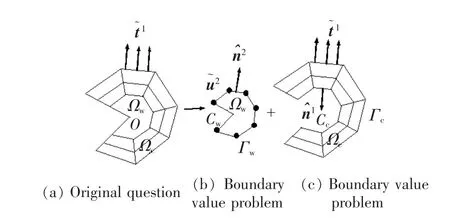
图2 二维角尖端网格划分Fig.2 Mesh division in a 2D corner-shaped domain
用H-R 原理建立超级V 型角尖端单元, 在Ωw域上的混合泛函形式简化如下
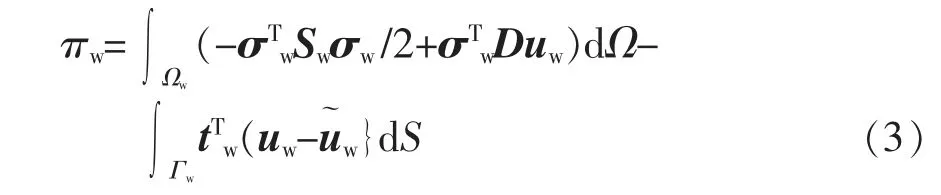
式中:带~的参数为边界上的定义;Sw为单元柔度矩阵;t 为边界应力向量;D 为材料弹性矩阵;σw为V型角尖端应力向量;uw为V 型角尖端位移向量;
通过构造位移场和应力场来简化H-R 泛函,使用散度定理进行降维运算。 对泛函πw进行变分,求解其稳态值,最终得到超级V 型角尖端单元的单元刚度矩阵。

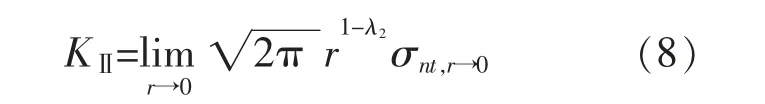
式中:σt,r→0,σnt,r→0分别为V 型角部尖端基于局部坐标系原点(n,t)附近的t 向应力和剪应力;λ1和λ2分别为张开型(Ⅰ模型)和滑开型(Ⅱ模型)对应的应力奇异阶数。
如图3 所示,在拉伸载荷下,两个沿x 方向排列的类钻石型孔洞。 由于对称,对右半平面进行了建模。超级V 型角尖端单元可用于计算孔洞的局部奇异性应力。 需要指出的是,角尖端单元的节点总数可能随其大小和位置而变化。 V 型角尖端o 周围网格的细化如图4 所示。 然而,在传统的有限元分析中,需要采用精细网格来获得V 型角尖端附近的奇异性弹性场。 在V 型角尖端处,细化后的单元边长最小尺寸约为10-5l。 新型超级奇异角单元法在网格划分方面具有简捷性[41]。
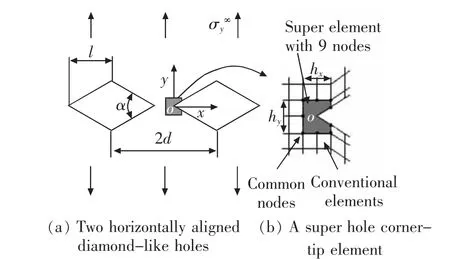
图3 拉伸载荷下两个水平排列的类钻石型孔洞Fig.3 Two horizontally arranged diamond-like holes under tensile load
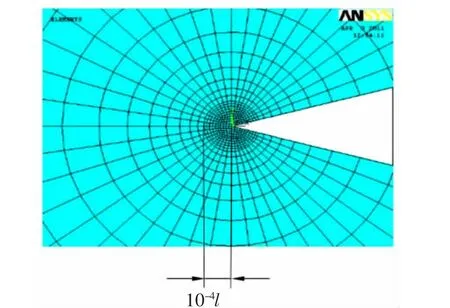
图4 类钻石型孔洞角尖端o 附近的传统有限元网格Fig.4 Traditional finite element mesh near the corner tip o of the diamond-like hole
各向异性材料的奇异性弹性场研究与各向同性材料大体相同, 不同点在于弹性矩阵不再为定值,会随着高斯点的变化而变化[42]。
各向异性双材料楔形问题的广义应力强度因子表达式为[43]

1.2 双材料楔形角尖端奇异单元
一般双材料楔形体如图5 所示,由两个楔形体组成。 两个楔形沿公共边结合在一起,该边构成一个界面。 双材料楔形体尖端的奇异性应力场取决于两方面问题:①是双材料楔形体的结构;②是双材料之间的属性匹配关系。 在求解奇异性应力场过程中,双材料楔形体尖端的数值特征解与单相材料楔形体是不同的。
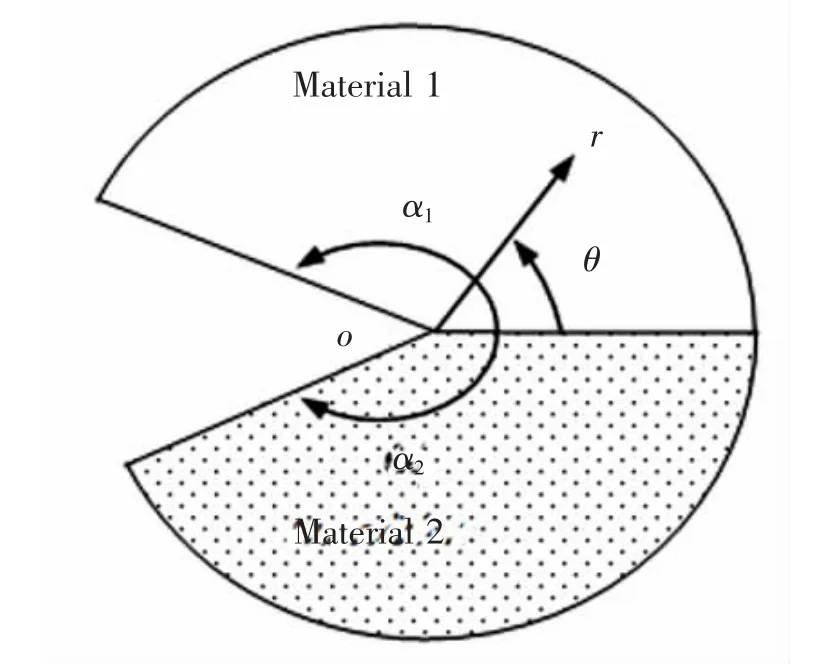
图5 一般双材料楔形体Fig.5 Definition of a general bimaterial wedge
值得注意的是, 楔形角尖端单元满足LBB 准则:应力参数个数,也就是待定系数βn的的个数应大于或等于所有节点自由度总数减去混合单元的刚体模式[44],二维问题的刚体模式为3。 图6 为建立的9 节点双材料超级角尖端单元。 对图7 所示的单轴拉伸界面上带有楔形缺口的双材料面板进行处理, 楔形体尖端域采用一个双材料超级角尖端单元,周围采用常规单元相结合。 分析结果精确,开发的双材料超级角尖端单元在处理楔形问题方面具有通用性和适用性[34]。
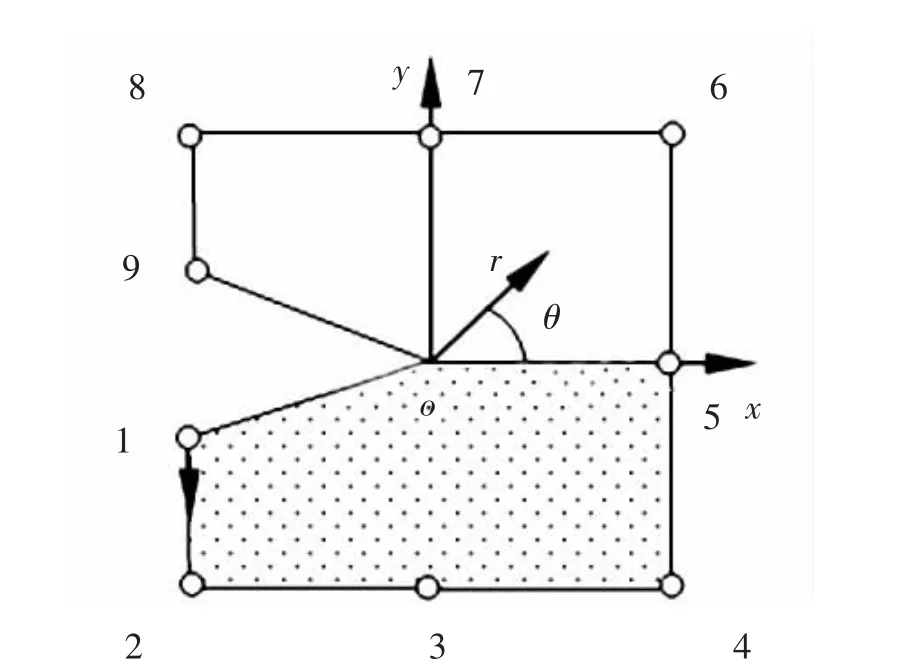
图6 9 节点双材料超级角尖端单元Fig.6 Definition of nine-node bimaterial super wedge-tip element
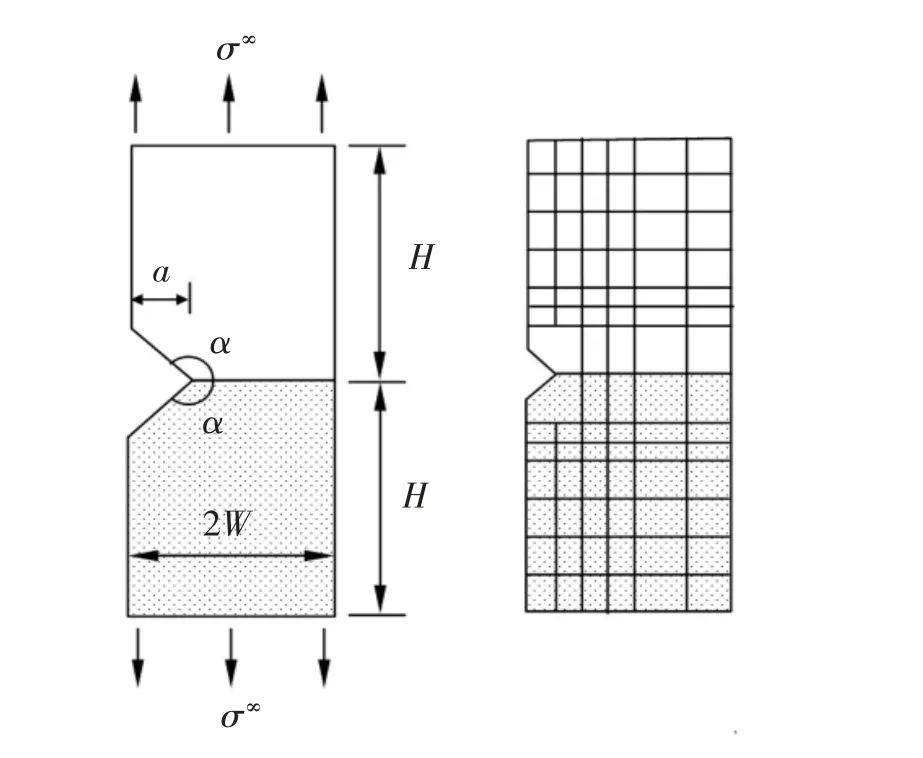
图7 双材料楔形角问题的几何尺寸和网格划分Fig.7 Geometry and mesh division for the bimaterial wedge problems
1.3 压电复合材料奇异单元
压电材料是具有压电特性的智能材料,例如一般电子监控设备中的传感器材料中就包含压电材料。 自Parton[45]以来,压电断裂力学的理论有一定发展,然而在这些研究中有一个缺陷:假定裂纹内部介质的介电常数为零,而实际情况是电场可以自由导通。 Scherzer 和Kuna[46]分析了嵌入式智能复合材料的裂纹结构。 在他们的研究中,裂纹面间的电边界条件仍然局限于非导通条件。 一般情况下,对于裂纹力学与电学不同状态,主要存在不导通、导通和有限导通三种边界条件。 不导通或导通的边界条件可以看作是部分导通的极限情况。 对于楔形裂纹,发现如果开口楔形角大于3.5°,则空气的介电常数可以忽略,也就是说,不导通条件的影响与导通边界条件的影响相同。
根据线弹性理论的应变位移关系和电场电势关系,可得到线性压电材料的本构方程[47]
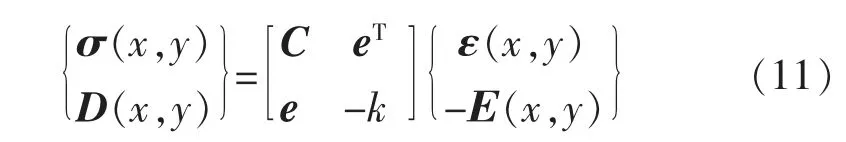
式中:σ(x,y)为应力张量;ε(x,y)为应变张量;D(x,y)为电位移张量;C 为压电材料弹性常数矩阵;E(x,y)为电场张量;e 为材料压电常数矩阵。
通过应力平衡方程、电荷守恒方程、应力自然及本质边界条件、电荷自然及本质边界条件求解平面压电材料的广义H-R 变分泛函为

针对材料裂纹尖端奇异性,应用超级角尖端混合元模型[34],通过分部积分和散度定理处理H-R变分泛函, 采用拉格朗日线性插值方法建立相邻节点间的形函数, 使单元间位移和电势自动满足相容性。 通过泛函∏的驻值条件,得到压电材料超级角尖端单元的刚度矩阵Kw。 建立包含部分角尖端的整个压电域的有限元代数方程, 确定整体位移U(x,y)和电势Φ(x,y),将超级角尖端单元进一步推广到压电断裂力学中[48-50]。
图8 为一个含9 节点的超级角尖端单元,用以分析楔形体顶点处的应力场强度和电弹场强度。 如图9 所示为远场拉伸载荷σy∞和电位移载荷Dy∞下含中心裂纹试件,该裂纹为部分导通。 由于对称,只考虑右半面板分析。 单元划分采用传统单元和超级角尖端单元组合形式。 沿正向x 轴(即x>0)的节点电势设为0。 通过奇异电场的数值解得到能量释放率, 结果精确, 并避免了在裂纹尖端划分高密度网格,提高了计算效率;通过裂纹尖端的应力强度因子和电位移强度因子结果发现, 裂纹面电边界条件对KⅠ和KⅡ影响不大,而对电位移强度因子KⅣ有较大影响,导通裂纹时,对应于Ⅳ型断裂模式的特征值λⅣ不再呈现-0.5 奇异性,表明电场奇异性很小[51]。
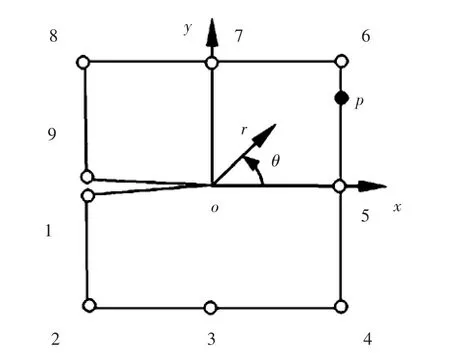
图8 9 节点超级角尖端单元Fig.8 A nine-node super corner-tip element
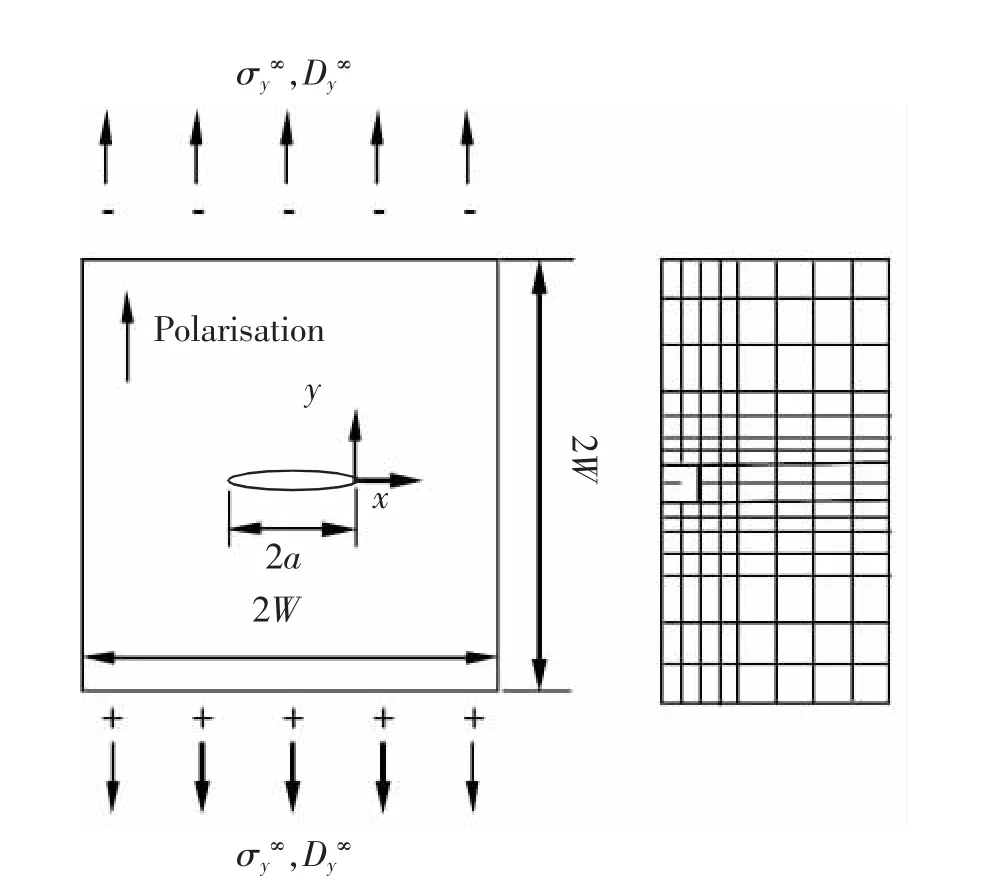
图9 压电平板中心裂纹问题的几何模型和网格划分Fig.9 Geometry and mesh division for the central crack problem in a piezoelectric pane
1.4 平面夹杂角尖端奇异单元
复合材料中,夹杂物的形状可以是圆形、椭圆形或其它不规则形。 在制造或使用过程中,夹杂界面处往往会出现应力集中, 裂纹可以在夹杂-基体界面或附近形核,影响耐久性。
为求解弹性材料中夹杂角的奇异弹性场,建立如图10 所示的含部分夹杂角的超级n 边形单元。将原始问题(图10(a))分解为:在夹杂域Ω2中的混合边界条件为C2,ΓA和ΓB(图10(b));在基体域Ω1中的混合边界条件为C1,ΓA和ΓB(图10(c))。同样,根据H-R 原理, 利用散度定理定义以下两个单独的混合泛函[52]
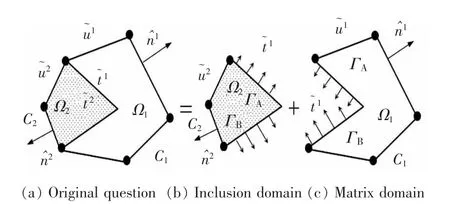
图10 单元分解Fig.10 Element decomposition

为了从两个分解问题的解中恢复原问题的解,需要在边界ΓA和ΓB施加牵引交换条件和位移协调条件
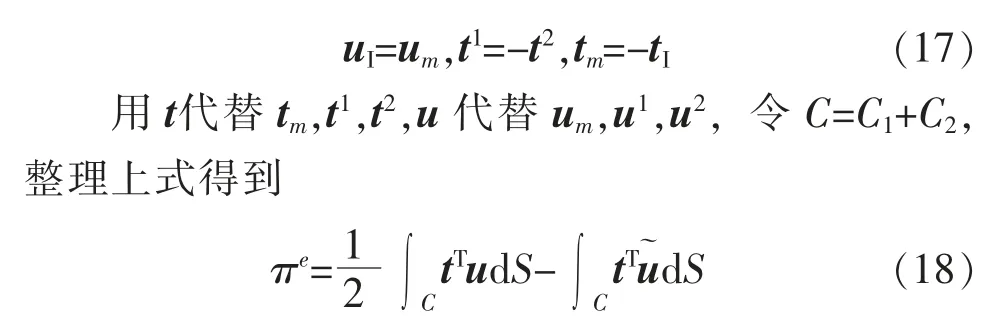
利用弹性材料夹角附近渐进位移和应力的一般表达式进而得到超级夹杂角尖端单元的刚度矩阵。 超级夹杂角尖端单元用于近场区域的建模,并与远场区域的传统4 节点单元结合,最终得到夹杂角附近的奇异性应力场[53-54]。
图11 为在平面应力条件下, 受拉伸和剪切荷载下包含矩形夹杂物的各向同性无限平板。 图12为矩形夹杂角附近网格划分的构型。 由于几何形状和载荷的对称性,有限元网格划分只需要几何形状的1/4。 在数值计算中,可以结合使用一个超级夹杂角尖端单元和285 个常规4 节点四边形单元。 相对于传统有限元,超级夹杂角尖端单元法能够节省夹杂尖端的网格数量,方便建立模型,提高计算效率。研究得到的无量纲应力强度因子数值结果具有精确性[55];对于单矩形夹杂物问题,当l/b>10 时,可以忽略l/b 对广义强度因子的影响, 将矩形夹杂物视为纤维。
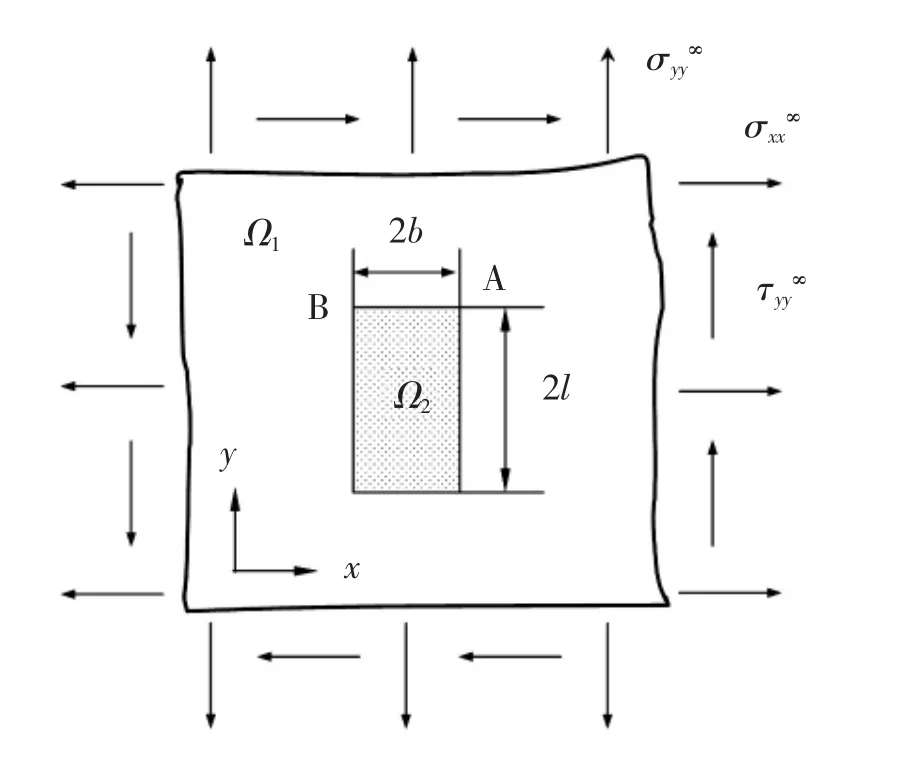
图11 夹杂物形态Fig.11 Configuration of inclusions
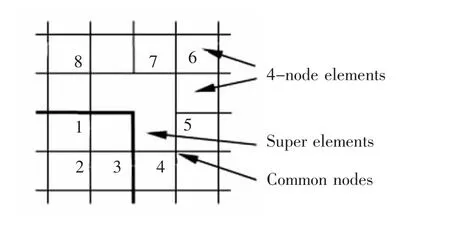
图12 矩形夹杂角周围的网格划分Fig.12 Configuration of mesh division around a rectangular corner
1.5 热-机载荷下的奇异单元
热-机载荷下由于材料弹性特性和热膨胀系数不匹配,在制造或使用期间材料界面处通常会出现高度集中的应力[56]。
1.5.1 热载荷下的等效奇异性应力场
对于由于温度变化而引起的奇异热应力场的变化问题,首先需要从物理角度出发,分析机械载荷与热载荷的关系,然后计算机械载荷作用下奇异性应力场,以及等效热载荷下的奇异热应力场。
如图13 所示: ①机械载荷σ0和温度变化△T下的无限基体平板与夹杂平板(图13(a));②切割某形状夹杂, 嵌入去除同形状基体平板的孔洞中,保持满足力学平衡条件和位移协调条件 (图13(b));③反向施加载荷σ0(图13(c))。
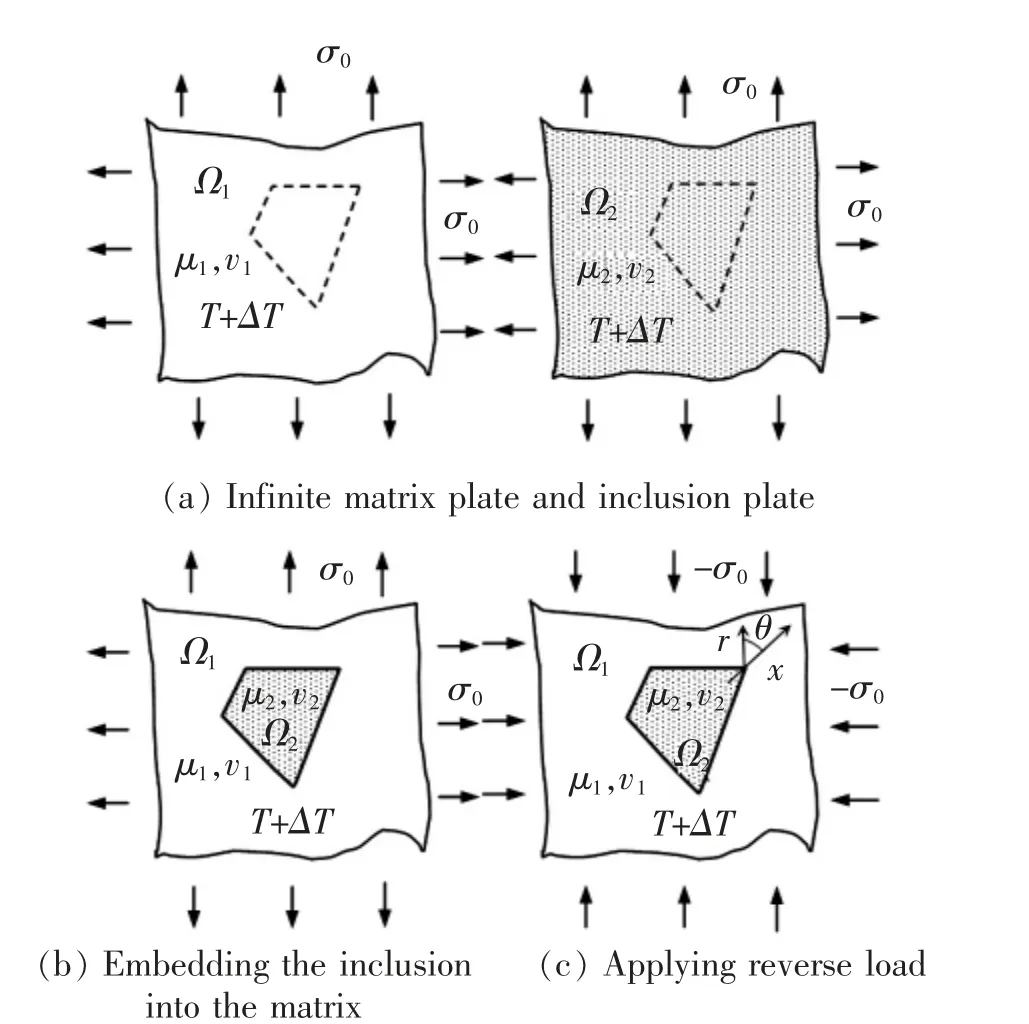
图13 ΔT 下的热应力场变化Fig.13 Change of thermal stress field under ΔT
经分析可知,在边界自由、界面全结合、温度均匀变化的条件下,夹杂角尖端奇异性应力场为

式中:(r,θ) 为以夹杂角顶点o 为原点的极坐标;σ0为机械载荷; KⅠ,λ1|σ0和KⅡ,λ2|σ0为σ0产生的Ⅰ型和Ⅱ型奇异性应力场强度因子;fⅠrr(θ),fⅡrr(θ)等分别为对应的Ⅰ型和Ⅱ型应力角分布函数;λ1,λ2分别为对应的Ⅰ型和Ⅱ型应力奇异指数。
由温度变化带来的奇异热应力场变化值等于远场机械载荷σ0导致的奇性应力和非奇性项相加,σrθ没有附加常数项。 温度变化产生热应力场的等效远场机械载荷为[57]
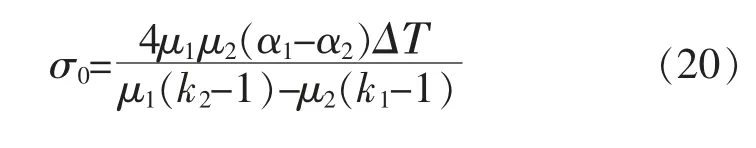
式中:μ1,α1,k1为基体材料参数, 包括剪切模量,热膨胀系数, 杨氏弹性模量;μ2,α2,k2为夹杂材料参数;ΔT 为变化温度。
对于夹杂尖端部奇异性热应力场分析,可以直接利用超级夹杂角尖端奇异单元法分析的机械载荷作用下奇异性应力场数值结果,计算奇异性热应力场数值解[57]。
1.5.2 热-机载荷下的超级楔形角尖端单元
在线性弹性理论中,温度变化下的本构方程与纯机械载荷下的本构方程不同。 在热机械载荷下,双材料楔形体中的应力和位移场可以写为


式中:qs和qc分别为超级楔角尖端单元和常规单元的公共节点位移向量;Ks和Kc分别为超级楔角尖端单元和常规单元的单元刚度矩阵;tFc为热载荷引起的节点反作用力向量;mFc为常规单元的边界牵引力向量;H,f为自定义矩阵[59];∏0为热负荷下的与位移和应力相关的总电势。
为了组装超级楔形角尖端单元和常规单元,令边界线处的节点对应的位移具有连续性。 对泛函∏t进行变分导出下式, 进而求解节点位移qc和热-机载荷下的奇异性应力场。

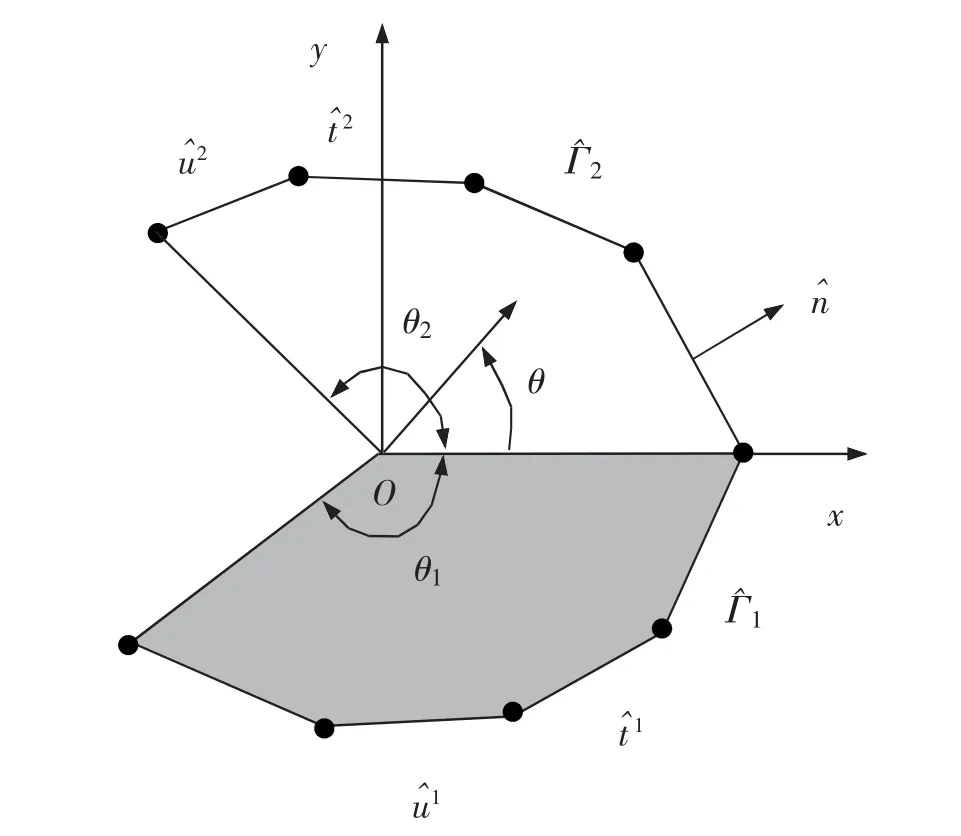
图14 超级楔形角尖端单元Fig.14 The super wedge-tip element
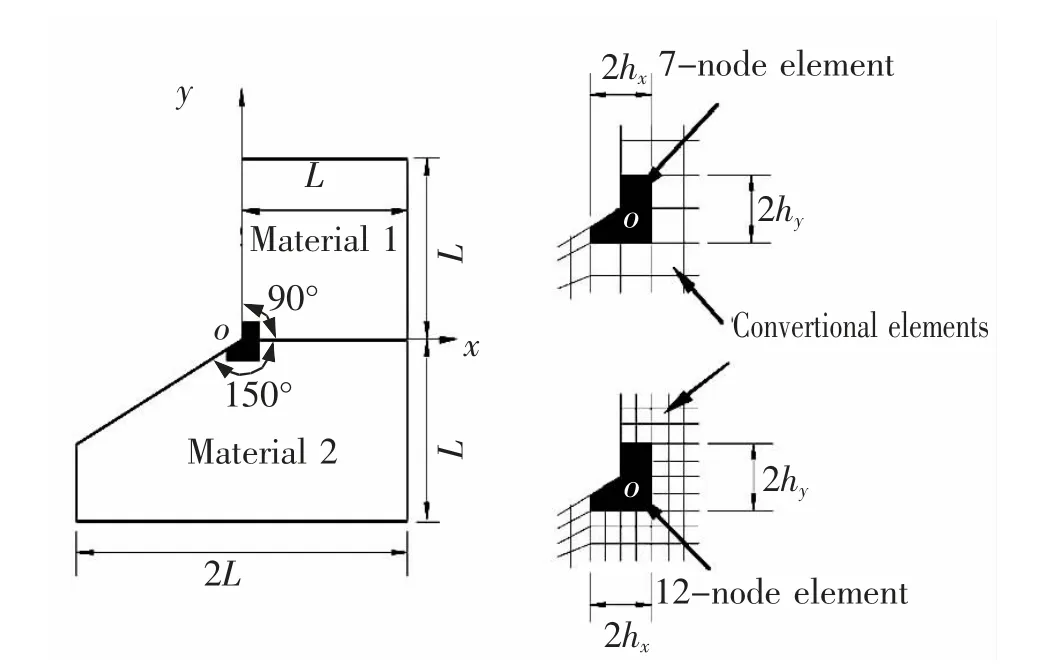
图15 具有90°~150°粘合楔形角结构Fig.15 The structure with a 90°~150° bonded wedge

1.5.3 热-机载荷下的超级夹杂角尖端单元
热-机械载荷作用下夹杂角尖端附近的奇异性应力场可以通过使用超级夹杂角尖端单元和混合应力单元来获得。 如图16 为夹杂附近的局部坐标系,x 轴位于夹杂角分线上,Ω1为基体域,Ω2为夹杂域。 热-机载荷下夹杂角尖端附近奇异性应力场的特征解与应力平衡条件、牵引交换条件和相容条件有关。
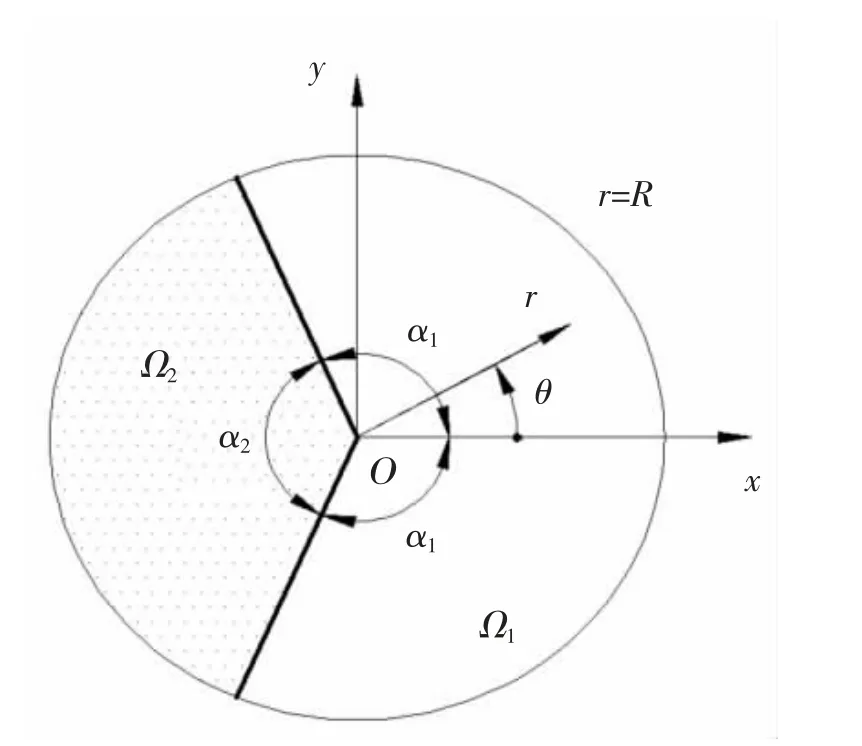
图16 夹杂附近的局部坐标系Fig.16 Local coordinate system near the inclusion
应力平衡条件为
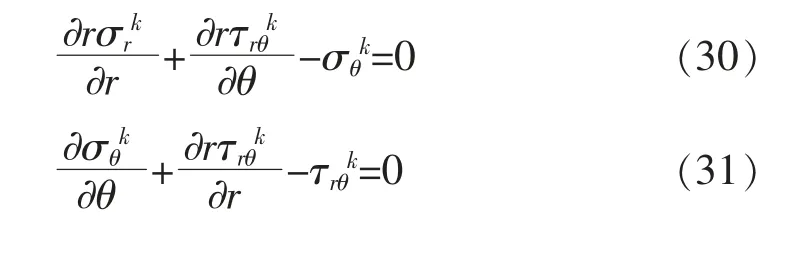
牵引交换条件为

从某种意义上说,上式中第2 项和第3 项是由位移而不是规定的牵引边界条件导出,它与传统的虚功原理是不同的。 如图17 为一个n 边型超级夹杂角尖端单元。 根据热-机载荷下夹杂角特征解建立插值函数。 建立的超级夹杂角尖端单元,能够保证超级单元和常规单元间公共节点的位移连续性。图18 为热载荷下含矩形夹杂物的矩形单胞, 均匀变化的温度为ΔT=100 ℃。 在夹杂角尖端采用一个超级夹杂角尖端单元,周围采用传统单元。 如图所示利用2 种超级单元来分析奇异性应力场:8 节点单元和16 节点单元。 2 种超级单元尺寸hx=hy=0.05l1;hx=hy=0.1l1。分析的奇异性应力场对超级夹杂角尖端单元的节点数量和单元尺寸不敏感,并且在粗网格的情况下能够提供令人满意的结果[60-62]。
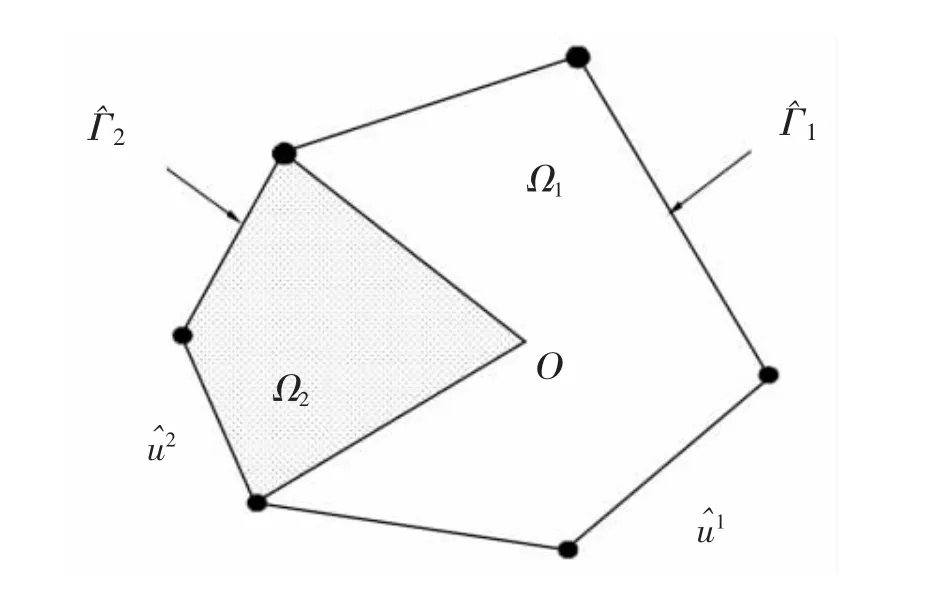
图17 n 边型超级夹杂角尖端单元Fig.17 Super n-sided polygonal inclusion corner-tip element
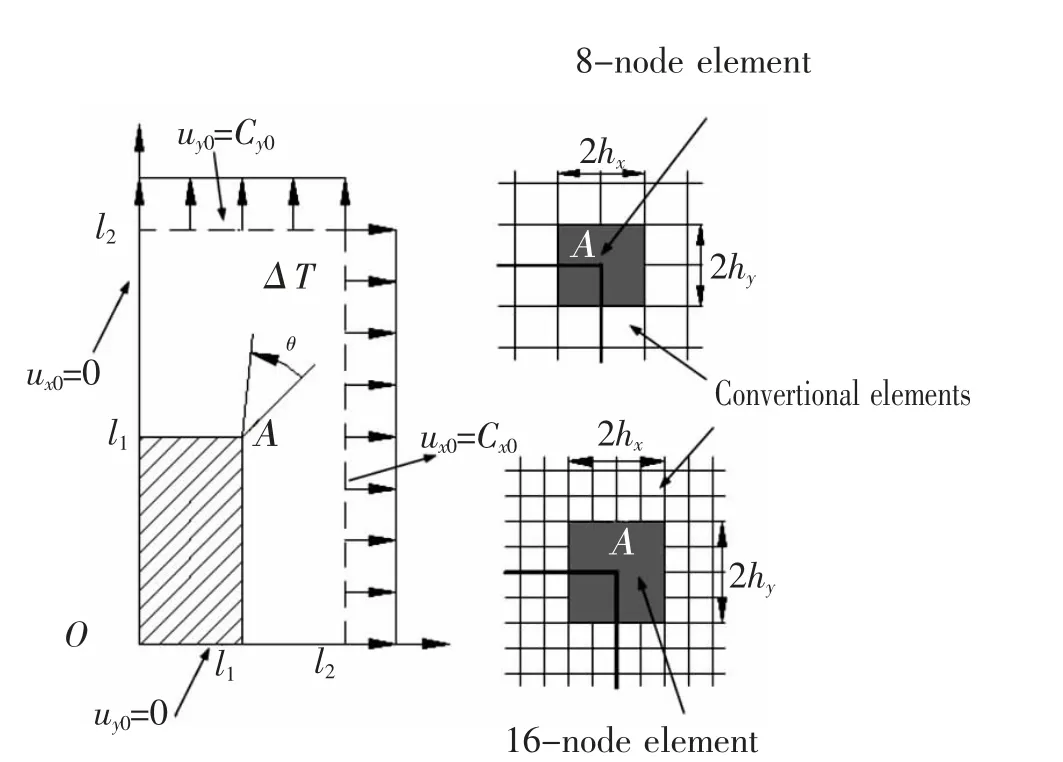
图18 热载荷下含矩形夹杂物的矩形单胞Fig.18 Rectangular unit cell containing a rectangular inclusion for pure thermal loads
2 三维楔形角尖端奇异单元
三维角部尖端问题所带来的数学困难远远大于二维角部尖端问题。 与二维问题不同的是,三维角部尖端附近的渐近场包含了3 种断裂模式。 目前三维问题研究的目标之一是解决角部前沿奇异性应力场。 为此,基于H-R 变分原理,提出一种新的包含部分角尖端的超级奇异三维单元。 由于解析本征解通常应用于简单构型, 数学推导过程较复杂,可以采用广义平面应变问题的一维有限元公式求解三维位移场和应力场强度。
2.1 包含直线角线的三维角构型奇异单元
如图19(a)所示为包含恒定二面角直边的三维均匀线弹性实体。 在这种情况下,一个沿直线角前沿的特定直线坐标z 轴可以代替一般曲线角问题的曲线坐标。 依据Sze 和Wang[63],任何法向平面的渐近位移和应力场可以由二维广义平面应变解推导而得。 根据控制方程的弱形式,由有限元特征分析方法来确定特征值[64]。
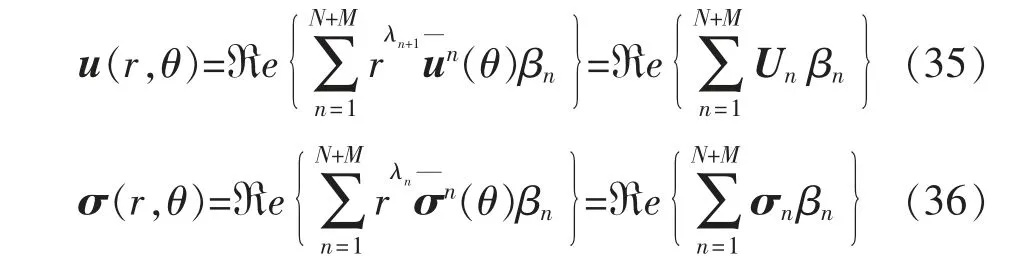
式中:u(r,θ)包含的位移分量为ur,uθ,uz;σ(r,θ)包含的应力分量为σr,σθ,σz,σrθ,σrz,σθz;ℜe{ }表示取复数的实部;λn为特征值;N 为复数特征值个数,M为实数特征值个数;βn为未知应力强度系数, 其与远场边界和载荷条件有关;un(θ),σ¯n(θ)分别为位移和应力角分布函数;Un是位移级数向量表达式的第n 项。
如图19(b)所示,为确定弹性材料中未知系数βn和计算围绕角尖端奇异弹性场,在笛卡尔坐标系中采用包含部分角尖端域的超级n 边单元。 根据Zhang 和Katsube[20]定义角尖端单元域问题的混合泛函形式
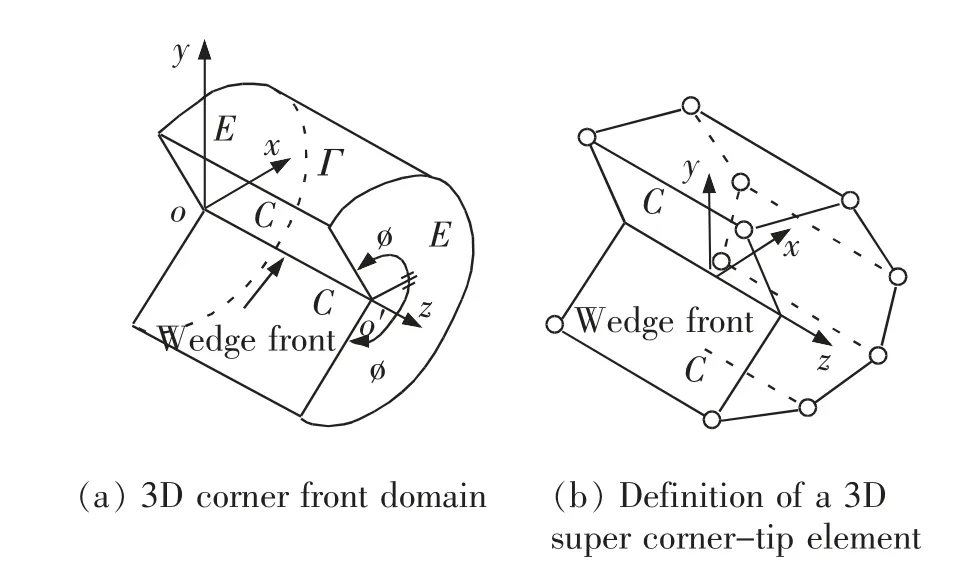
图19 包含直线角线的三维角构型奇异单元Fig.19 Three-dimensional angular configuration singular element containing straight corners

为求解泛函的驻值,构造应力和位移场,通过散度定理进行泛函简化[64]。在三维问题中,βn随z 值的变化而变化。 引入新的自然坐标建立三维角尖端等参单元。 通过极坐标和笛卡尔坐标的位移和应力转换,利用δπ=0 得到公式

图20 所示为沿厚度方向有阶跃变化的复合材料层压板。 图21 展示了两种具有不同三维角构型奇异单元的网格划分形式。 图21(a)和图21(b)分别包含一个14 节点和一个26 节点的奇异单元。 两种模式的单元尺寸不同, 但分析结果令人满意,而相同区域内,Pageau 和Biggers[7]则需要一个包含182个集中单元才能获得满意的结果。 三维角构型奇异单元比集中单元的数量要少,具有高效性。 应用建立的三维角构型奇异单元,还可以分析三维贯穿中心裂纹问题、三维单边裂纹问题和三维对接接头问题的奇异性应力场[64]。
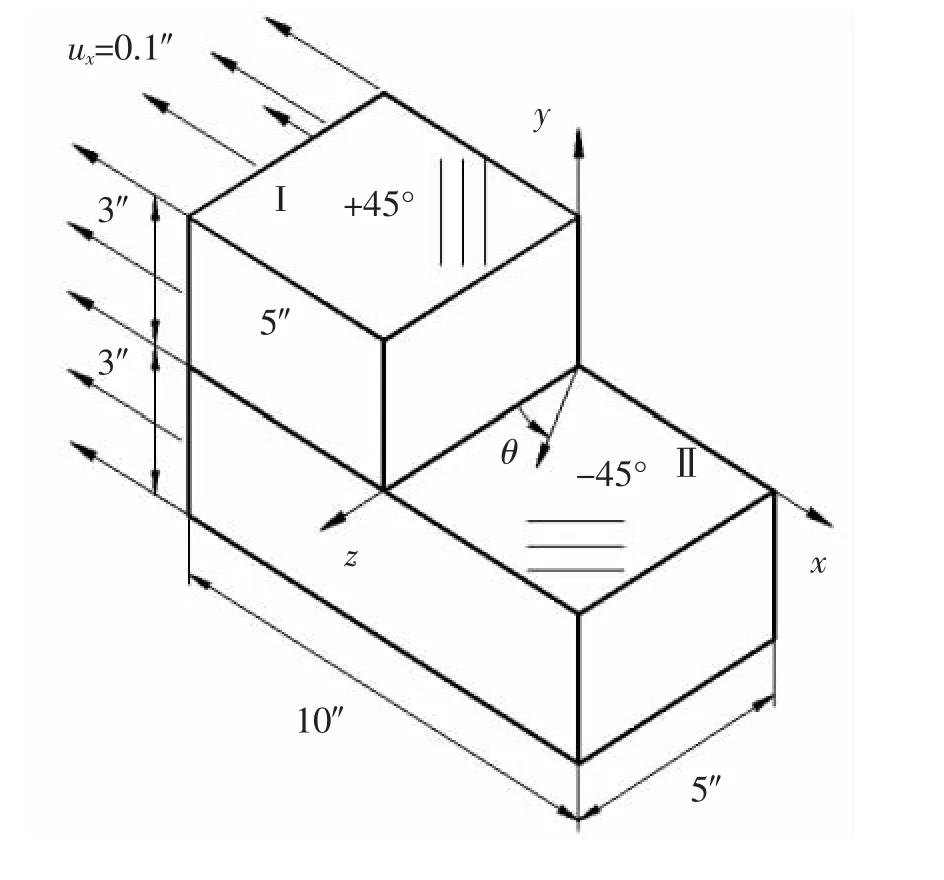
图20 厚度有阶梯变化的复合材料层压板Fig.20 Composite laminate with step change in thickness
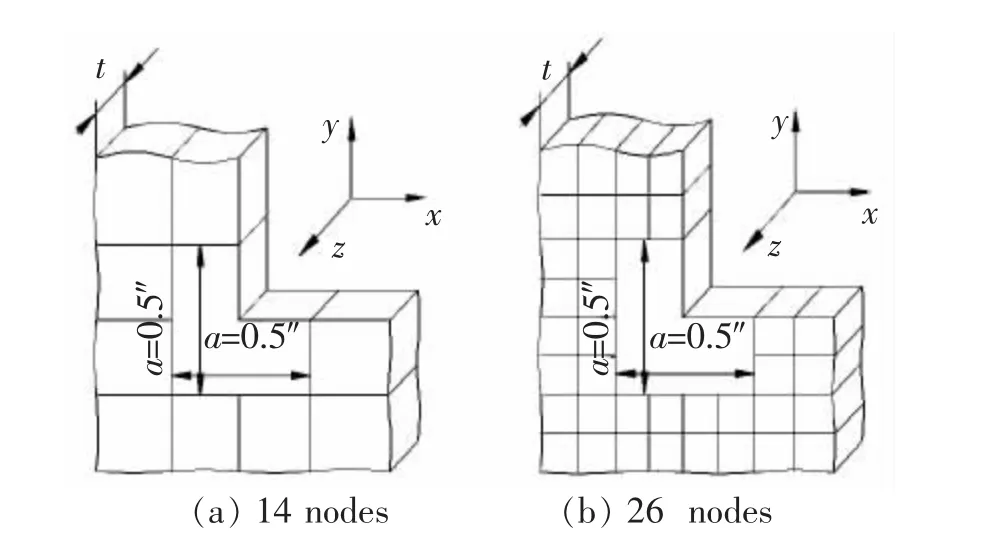
图21 两种不同的超级三维角尖端单元网格Fig.21 Meshes with two difference kinds of 3D corner-tip elements
2.2 三维曲线裂纹前沿奇异单元
在疲劳裂纹扩展过程中,裂纹前沿通常为曲线形状(如圆形裂纹或椭圆裂纹),必须考虑裂纹问题的三维特征[65]。 Ayhan 等[66]采用三维富集有限元计算了曲线裂纹的应力强度因子, 模拟了疲劳裂纹扩展,而利用富集有限元必须面临3 个困难:①数值结果仍然取决于特殊单元的大小; ②由于节点处的自由度不同, 不能满足特殊单元与常规单元之间的单元间兼容性, 通常需要过渡单元将特殊元素与常规单元结合起来; ③级数解的阶项不包含刚体运动模式, 在常规有限元方法中必须与位移插值一起使用。
基于奇异性位移场和应力场的数值特征解和H-R 变分原理, 建立包含部分三维曲线裂纹前沿的奇异单元,可以求解包括应力奇点阶数、位移角和应力角变化在内的数值系列特征解, 用于三维实体中的硬币形裂纹、 圆柱体中的周向裂纹和无限体中的椭圆裂纹等问题分析[67]。在曲线裂纹前沿附加的笛卡尔(x,y,z)和圆柱坐标(r,θ,z)中建立局部曲线坐标系(ρ,ø,θ),可以方便地描述裂纹前沿附近的局部变形行为。 对于裂纹尖端的弹性渐近场可表示为
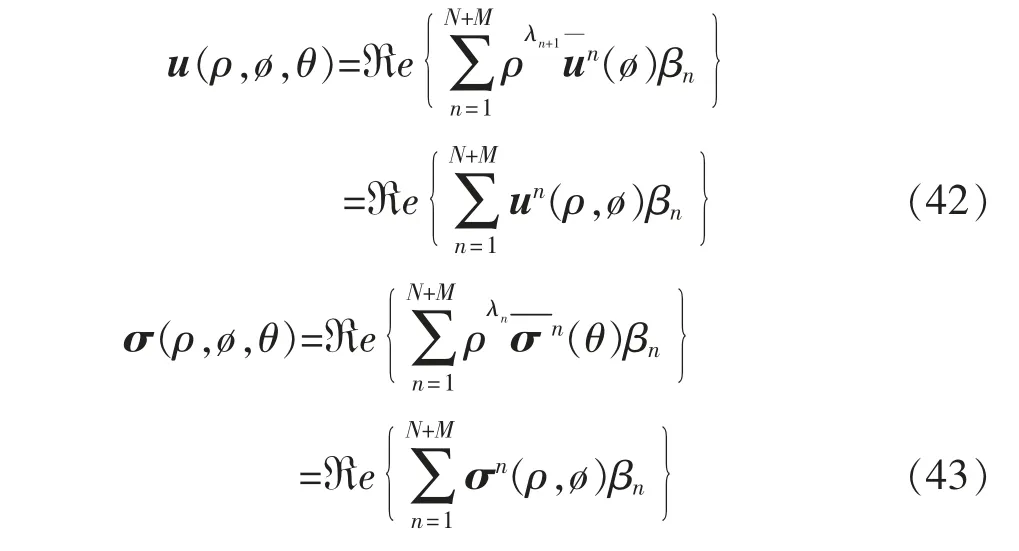

一般来说,沿任意曲线裂纹前沿不同法向面上的奇异性位移场和应力场的强度不是恒定的。 为了解决三维效应的影响, 建立如图22 所示的三维曲线裂纹前沿奇异单元。 单元域由两个端面Γe和一定数量的周向面Γc包围。 在三维曲线裂纹前沿奇异单元中,需要引入另一个自然坐标η 来表示裂纹前沿法平面ρ-ø。此外,还需定义用于离散化裂纹前沿位移和应力角变化的自然坐标ξ。 因而系数向量β 可以被认为是η 的线性函数。 在局部三维坐标系(ρ,ø,θ)定义位移和应力函数
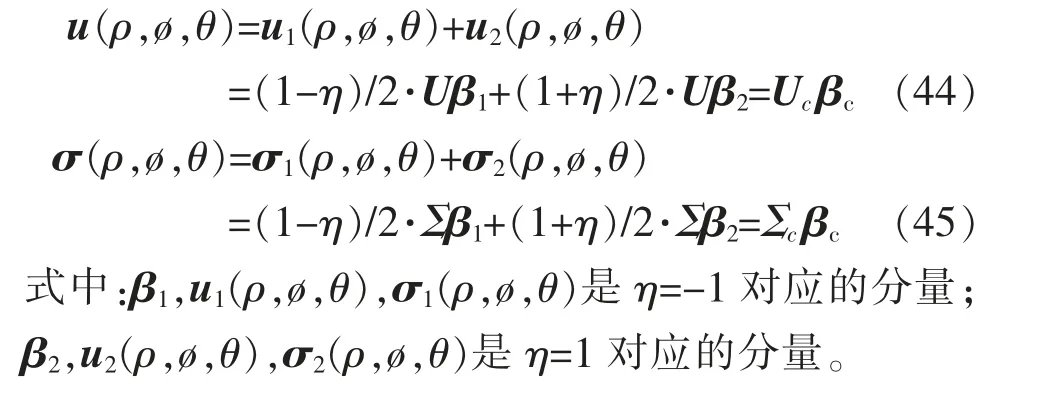
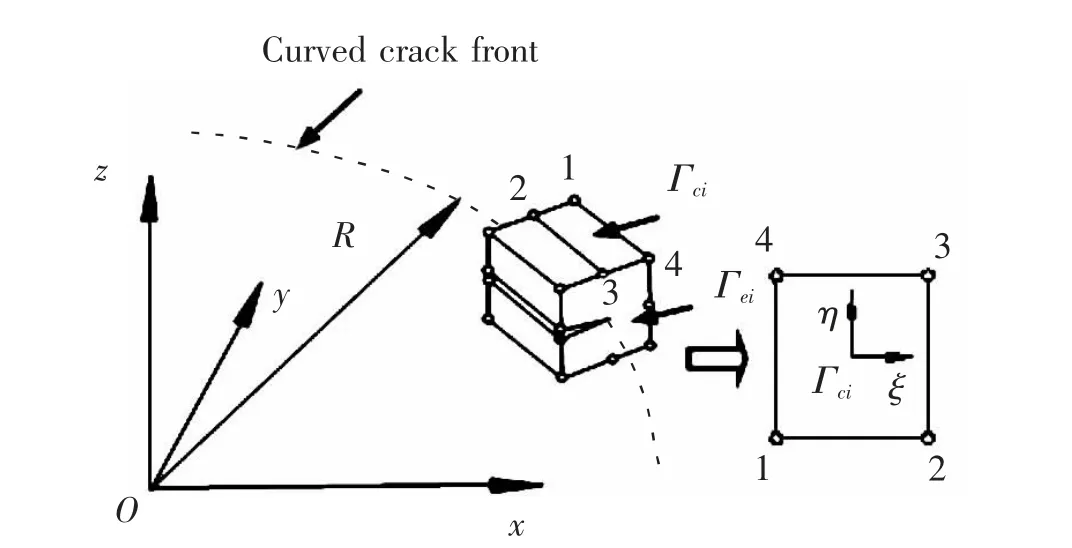
图22 包含部分曲线裂纹前沿的超级单元Fig.22 A super element containing a part of the curved crack front
为了获得三维曲线裂纹前沿奇异单元的刚度矩阵,需要利用H-R 变分的驻值和散度定理,通过位移边界条件求解[67]。图23 为承受扭转载荷下的含硬币形裂纹。 为了清楚地说明裂纹前沿附近的网格划分,图24 中绘制了模型的四分之一,在这种情况下, 沿裂纹前沿分布一定数量的超级18 节点三维曲线裂纹前沿奇异单元,其周围是传统的三维8 节点单元。 当单元尺寸小于或等于0.02a×0.02a 且单元数大于30 时,数值结果可以趋于收敛。 分析周向裂纹问题的应力强度因子表明, 当使用超过30 个单元时, 即使应用尺寸为0.1a×0.1a 的奇异单元也足以得到收敛解[67]。
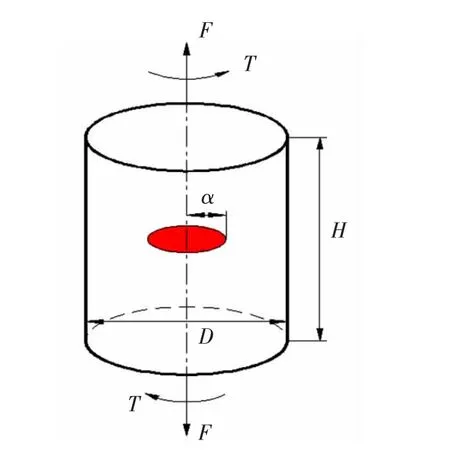
图23 扭转作用下的币状裂纹Fig.23 A penny-shaped crack problem subjected to torsion loading
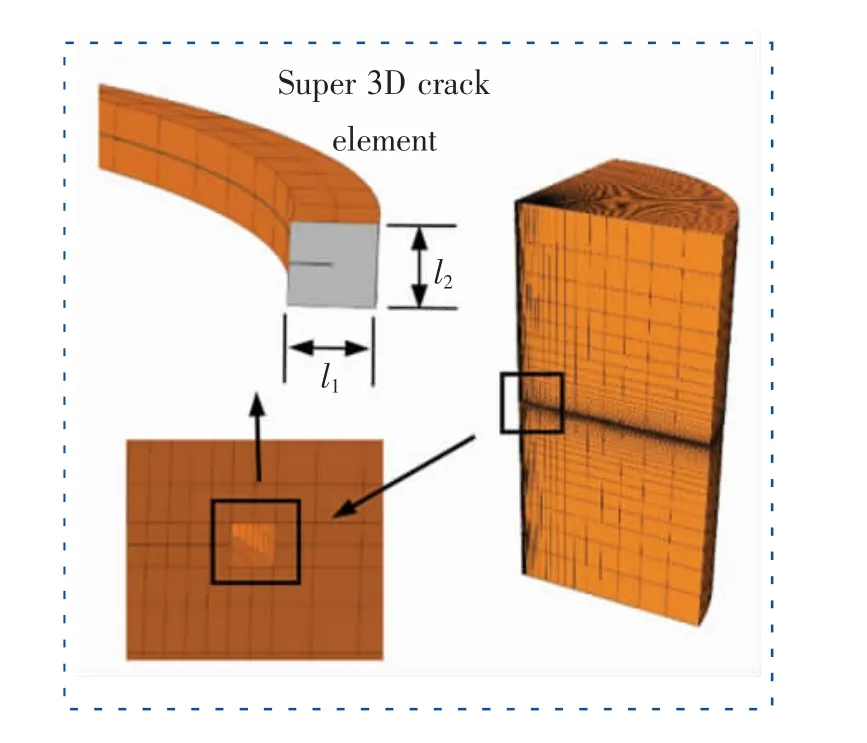
图24 币状裂纹的网格划分Fig.24 Mesh division for the penny-shaped crack problem
2.3 三维V 型缺口前沿奇异单元
大多数情况下,缺陷端部通常不是圆形或椭圆形状。在孔边可能出现V 型角引起的局部奇异应力导致严重的损伤或疲劳断裂。三维V 型角前沿奇异场的研究与三维裂纹奇异场研究原理相似, 但与Griffith 裂纹问题不同的是,V 型角的应力奇点数值特征解一般不等于-0.5, 奇异性应力场也随夹角的变化而变化。如图25(a)为三维类钻石型缺陷。为了求解三维V 型角附近的三维奇异性应力场和相应的高阶项级数解,采用广义平面应变问题的特殊有限元方法[63],在局部坐标系中确定数值特征解。通过该方法可以得到应力奇异性的阶数λn,以及位移和应变的角变函数un(ø,θ)和εn(ø,θ)。
局部坐标系中V 型角前沿的位移场u(ρ,ø,θ)和应力场σ(ρ,ø,θ)的一般表达式为
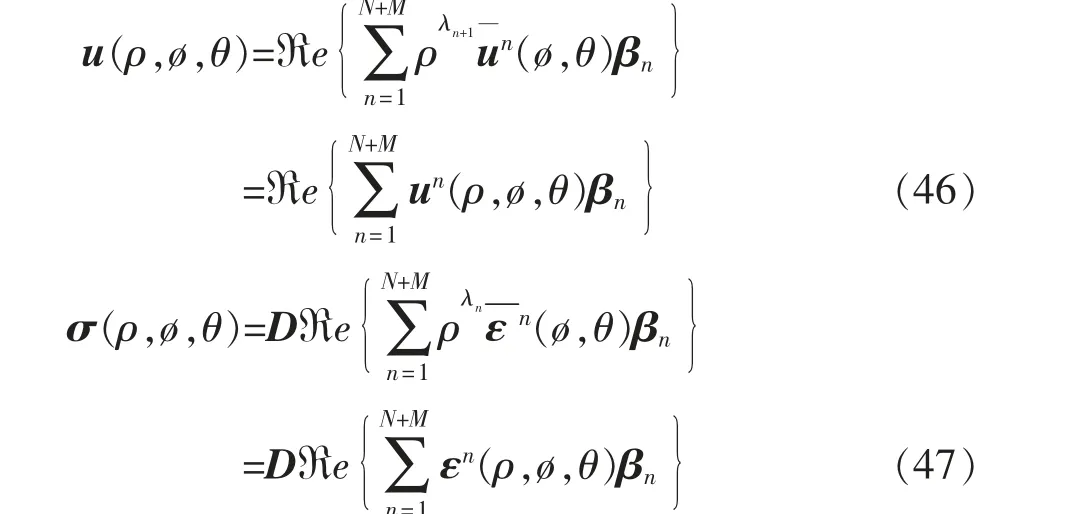
式中:βn为应力强度参数;D 为线弹性材料的弹性常数矩阵;u¯n(ø,θ),εn(ø,θ)分别为位移和应变角分布函数;un(ρ,ø,θ),εn(ρ,ø,θ)是位移级数向量表达式和应变级数向量表达式的第n 项。
在任意外载荷作用下,V 型角前沿的应力强度不是恒定的。如图25(b)所示可以建立三维V 型缺口前沿奇异单元来解决目前的三维V 型缺口问题。 利用局部坐标系下的位移和应力函数, 得到H-R 变分泛函和三维V 型缺口前沿奇异单元的刚度矩阵[68]。
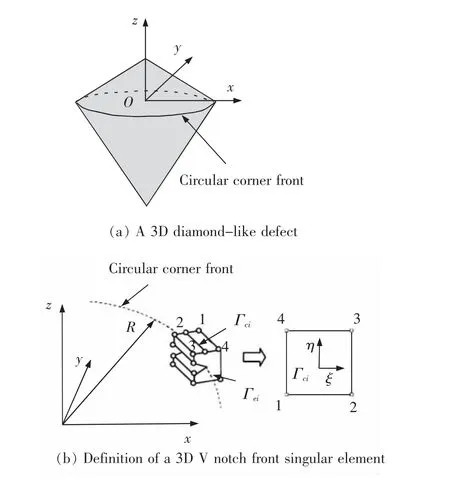
图25 三维V 型缺口问题Fig.25 Three-dimensional V-notch problem
为了将传统单元与三维V 型缺口前沿奇异单元组合起来,在公共节点上使传统单元与奇异单元的刚度矩阵进行组合。
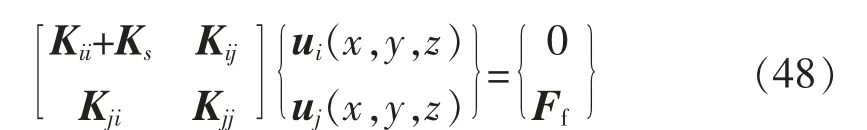
式中: 下标i 和j 分别表示公共节点域和非公共节点域;ui(x,y,z)和uj(x,y,z)分别表示公共节点和非公共节点的位移;Ff是等效节点力向量;Ks为奇异单 元 的 刚 度矩阵;Kii,Kij,Kji,Kjj分 别 是传统 单 元 刚度矩阵的分量。
采用新型有限元法计算圆杆中V 型缺口广义应力强度因子,如图26 所示,沿四分之一周角前沿分布40 个超级单元,周围采用传统单元。 在向量β维数小于24 时,数值结果的计算精度令人满意,这意味着三维V 型缺口前沿奇异单元的收敛结果很容易得到。 应用此方法可以进一步分析嵌入类金刚石缺陷、接近自由表面缺陷、表面缺陷、缺陷干涉等模型的应力强度问题[68]。
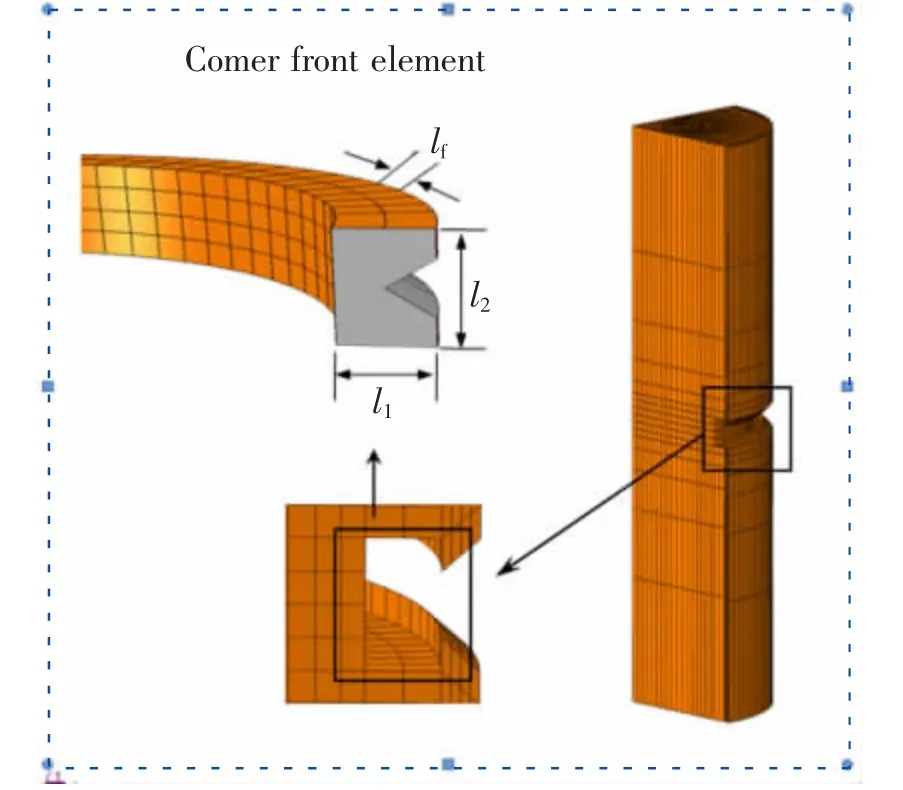
图26 含周向V 型缺口的圆形杆件网格划分Fig.26 Mesh division for a round bar with a circumferential a V-shaped notch
2.4 三维曲线型界面角前沿奇异单元
孔洞周围的应力集中可能导致双材料界面的退化和损伤,这是双材料界面结合强度减弱的重要原因,有必要建立相应的方法求解孔洞与界面交线附近的力学行为,以确定界面角尖端处的应力奇异强度。 双材料界面与三维轴对称孔洞的相互作用将形成一个周向的界面角,界面角可以是尖角或不同角度的钝角。 三维孔洞几何形式的复杂性增加了求解渐近应力场和边值问题的难度。 如图27,以双材料圆周界面线上点O 为中心建立局部曲线坐标系(ρ,ø,θ), 孔洞与ρ-ø 平面交点的曲率半径记为rI。基于局部曲线坐标系建立三维曲线型界面角前沿奇异单元,单元包含部分圆周界面角线,由两种不同体积的弹性材料V1和V2组成。 为了建立奇异单元的有限元方程,用界面边缘奇异性应力场的渐近解来离散位移和应力,引入一个自然坐标η 来描述角坐标θ 的位置。
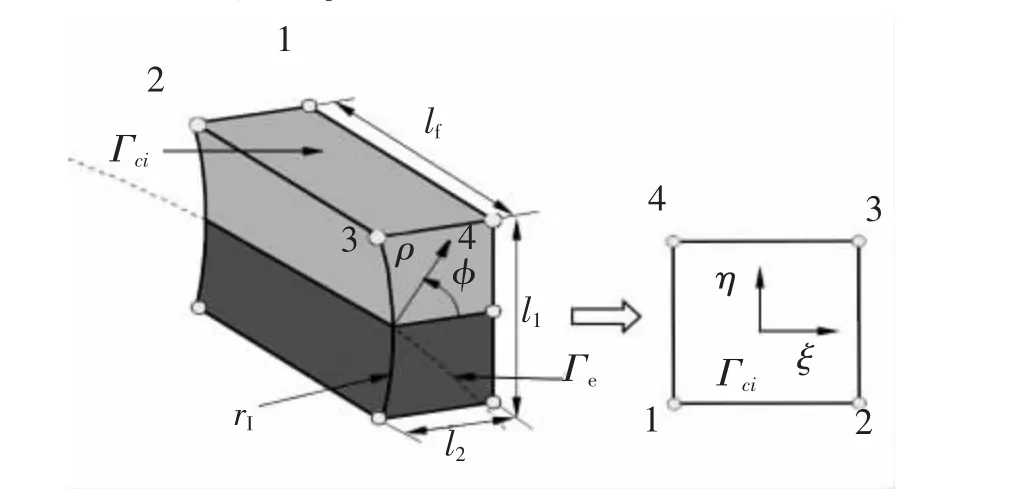
图27 包含部分周向界面交线的奇异界面单元Fig.27 A singular interface edge element containing a part of the circumferential interface intersection line
三维曲线型界面角前沿奇异单元域的泛函形式为
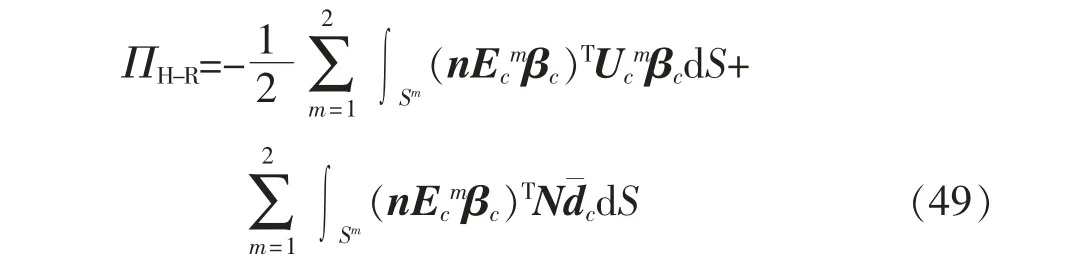
式中:N 为4 节点四边形单元的形状函数矩阵;n 为边界Sm外法线向量矩阵;βc为应力强度参数;Ecm和Ucm分别为自定义应力和位移矩阵[69];dc为含4 节点四边形单元所有节点分量的位移向量。
应用泛函驻值条件δΠH-R=0,导出奇异单元的刚度矩阵
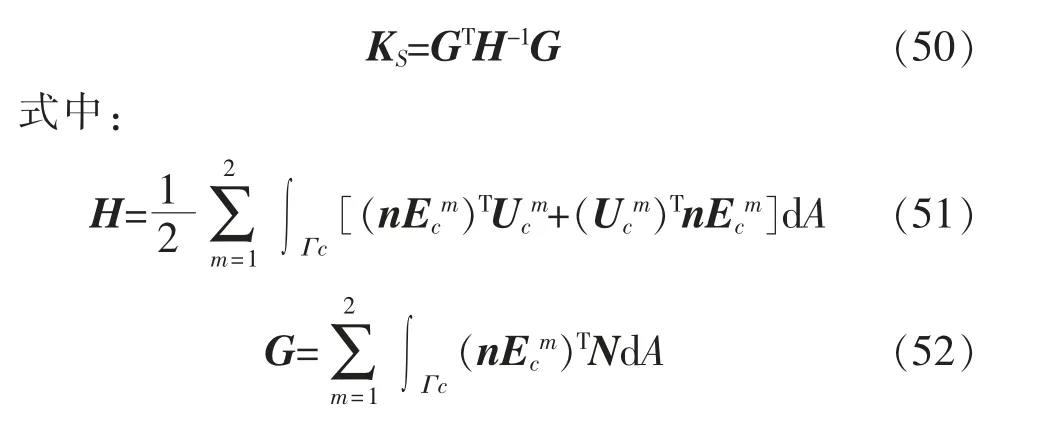
式中:Γc为奇异界面单元的周向界面,如图27 所示。
对于图28 所示的界面孔洞问题, 几何模型可以看作是包含有限界面孔洞缺陷的无限固体问题。为了避免当前双材料界面与三维轴对称孔洞交线附近的网格细化问题,在三维曲线型界面角前沿采用奇异单元,周围使用传统三维单元。 图29 显示了新型有限元法与传统有限元法在界面角尖端附近的网格划分区别。 如图29(a)所示,传统有限元在圆周线附近,使用高度细化的网格。 如图29(b)所示, 沿双材料界面和孔洞的周向交线上使用了30 个奇异单元, 新型有限元方法数值分析结果具有精确性[69]。
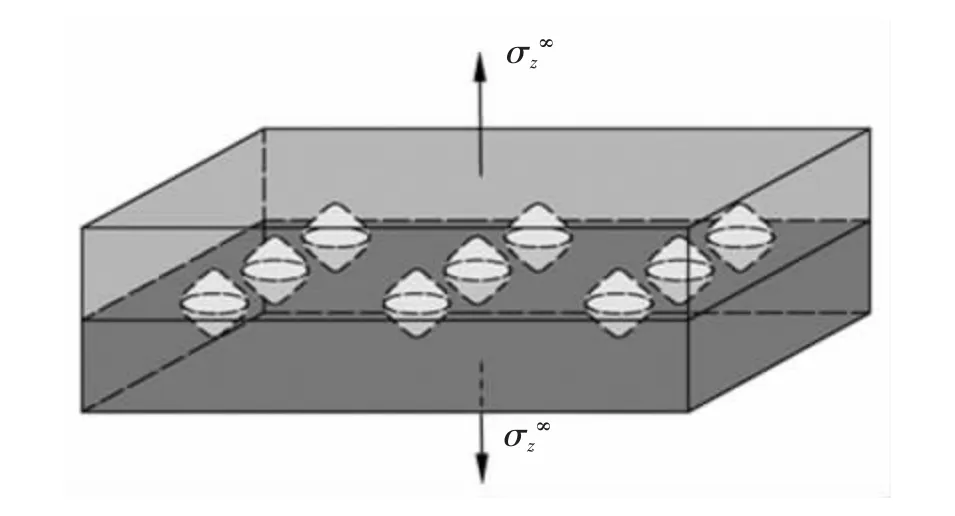
图28 双材料界面三维孔洞Fig.28 3D defects at the interface of a bimaterial
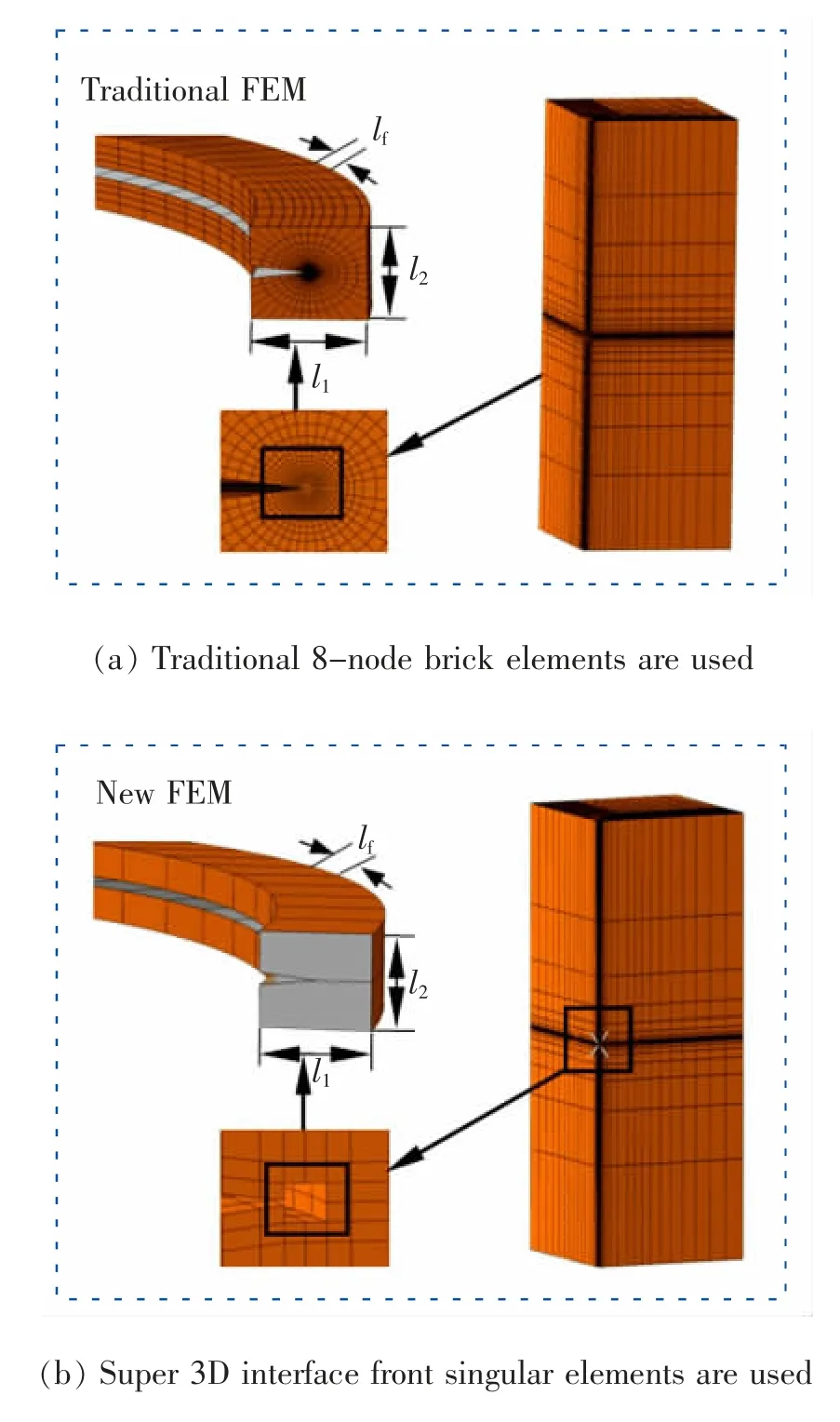
图29 含三维孔洞问题的网络划分Fig.29 Mesh division for problems with 3D voids
3 结束语
本文主要综述了新型超级奇异单元在二维或三维中的裂纹尖端、夹杂角尖端、V 型缺口角尖端、孔洞角尖端、多相材料界面角尖端的应用情况。 与其它奇异单元相比,新型超级奇异单元具有以下特点:
1) 奇异单元和常规单元之间节点处自由度一致,无需任何过渡单元即可与常规单元连接,单元相容性好。
2) 超级奇异单元在相对较低的计算成本下可以获得优异的结果,是分析二维或三维中的裂纹尖端、夹杂角尖端、V 型缺口角尖端、孔洞角尖端、多相材料界面角尖端的奇异性应力场的有效方法,适用性广。
3) 可应用于任意楔形角和任意材料组合的奇异场问题,具有良好的通用性和工程应用前景。
4) 新型超级奇异单元分析结果与单元尺寸无关,具有较高的稳定性。
5) 可以用于分析各向同性、各向异性和压电材料奇异电弹性场,可以解决热-机耦合载荷和机-电耦合载荷作用下的奇异性应力场。
6) 在三维应用领域,新型超级奇异单元只能对角部尖端线为光滑连续曲线或直线的奇异性应力场进行计算,对几何不连续角前沿线奇异性应力场的分析目前还有一定的局限性,需要进一步研究发展。
