高速移动荷载作用下无砟轨道路基动位移研究

冯靖淳，罗文俊，徐鑫洋，杜 可

（华东交通大学土木建筑学院，江西 南昌 330013）

近些年我国高铁步入快速发展时代，具有完全自主知识产权的“复兴号”于2017 年投入运营，实现350 km/h 运营，中国成为世界上高铁商业运营速度最高的国家[1]。 高速铁路迅速发展的同时伴随产生的路基动力学及岩土工程问题不容忽视。 列车在线路上高速运行产生的荷载传递至轨道结构，然后向下传递至路基及路基土体，在路基土体中产生振动和变形，加剧轨道结构的不平顺，从而影响列车运行的平稳和安全性[2]。

目前已有一些学者针对列车高速移动荷载对路基土体产生的影响开展过研究，Chebli 等[3]利用周期性假定，提出了土体-铁路轨道系统三维模型，考虑土-结构动力相互作用， 研究了高速移动荷载作用下有砟铁路轨道的响应。 聂志红等[4]基于层状梁和黏弹性半空间体理论建立轨道-路基耦合动力分析模型，考虑轨道和路基的耦合作用，利用移动坐标和双重傅里叶变换， 得到系统稳态响应解，对移动荷载作用下路基表面位移进行了研究。 Eason[5]利用傅立叶变换求得移动荷载作用下半无限弹性体内的应力解。 薛富春和张建民[6-7]建立了精细化非线性高速铁路轨道-路基-地基耦合模型，得出了竖向动位移沿线路横向在路基各结构层地面近似均匀分布，沿深度按照指数函数衰减的结论。 Kim[8]研究了弹性连续体结构在分布移动荷载下的动力问题。Auersch[9]运用有限元和边界元建立了轨道-地基模型， 分析了列车荷载作用下的地面振动问题，结果表明地面振动的频率成份以低频为主。 已有研究工作取得了一些进展和成果，但动荷载模拟及采用的轨道路基模型等仍有一些值得商榷的地方，例如：模型采用对称结构进行简化，造成动力响应数值在空间传播时产生一定的误差；在涉及地基土这种无穷边界区域的动力分析中，人为地截断地基土边界会使波在边界面上的反弹，反弹回来的波会对分析区域的结果产生影响，实际上，波会向无穷远方向传递；在模拟列车移动荷载上没有考虑到轨道随机不平顺等因素对轮轨载荷产生的影响，轮轨载荷模拟不够精确等。

针对上述问题， 本文通过多体动力学软件UM建立车辆-轨道垂向耦合精细化模型和有限元软件Abaqus 建立无砟轨道-路基-天然地基土非线性数值分析三维有限元模型，通过Fortran 语言二次开发子程序VD LOAD，将轮轨载荷加载到模型上，基于大规模计算技术研究了高速移动荷载作用下无砟轨道路基的动位移随时间、空间的变化规律，以期为高速铁路路基修建、运营维护及评价提供一定的理论依据。

1 模型分析

1.1 模型概述

模型整体由无砟轨道-路基-土体组成，模型如图1 所示。 无砟轨道结构包括钢轨、轨道板、自密实混凝土及混凝土底座；路基包括基床表层、基床底层及基床以下路堤本体部分；地基土体为天然地基土。模型整体沿轨道前进方向的长度为130 m，宽度方向为60 m， 地基土厚度取为30 m， 其余尺寸按《高速铁路设计规范》 及相关研究确定参数并建立模型[10-11]。

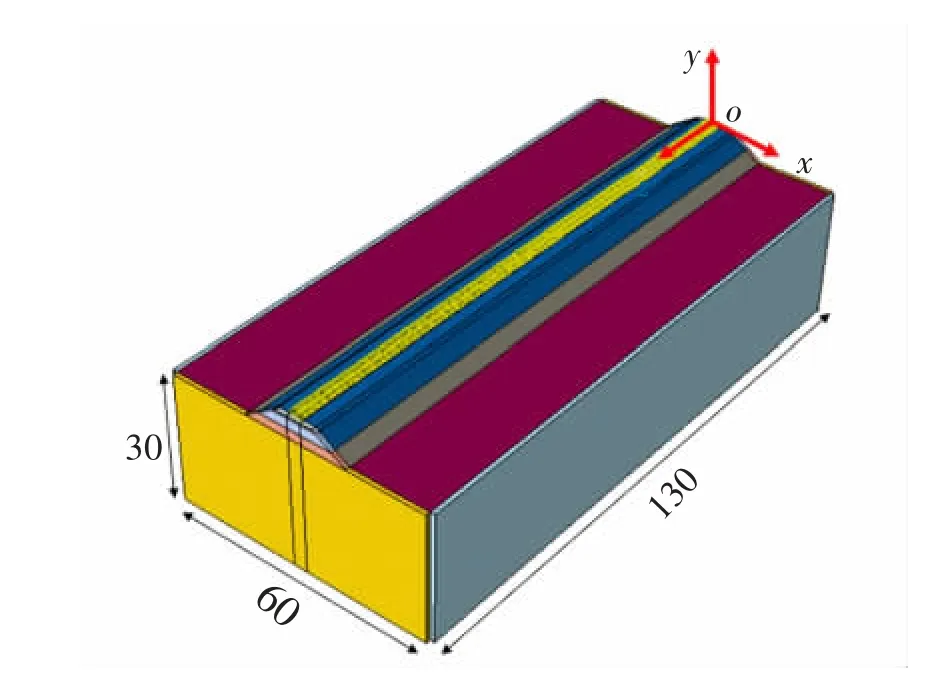
图1 三维整体模型（单位：m）Fig.1 Three-dimensional overall model（Unit：m）

1.2 模型参数和本构关系

1.2.1 轨道结构

本文采用的是高速铁路的CRTSⅢ型板式无砟轨道，全程采用无缝线路，断面尺寸如图2 所示，在实际应用中钢轨的截面较为复杂，在以往的研究中大多将钢轨工字型截面进行简化处理， 考虑为矩形截面，且在对轨道板的模型建立过程中，通常忽略了轨道板之间的伸缩缝， 导致轨道板内部的附加应力对计算结果造成影响，产生一定的误差，故本文钢轨采用我国的T60 钢轨，截面面积7.725×10-3m2，截面惯性矩3.217×10-5m4， 每块轨道板之间的伸缩缝间距设置为70 mm。 轨道结构除钢轨和轨道板之间的扣件外，其他均采用线弹性本构模型，材料参数见表1， 本文模型将扣件系统模拟为线性的弹簧-阻尼单元，扣件间距为0.63 m，其横向，垂向，纵向的动刚度分别为50，35，15 kN/mm，横向、垂向、纵向的阻尼系数分别为50，48，46 kN·s/m。

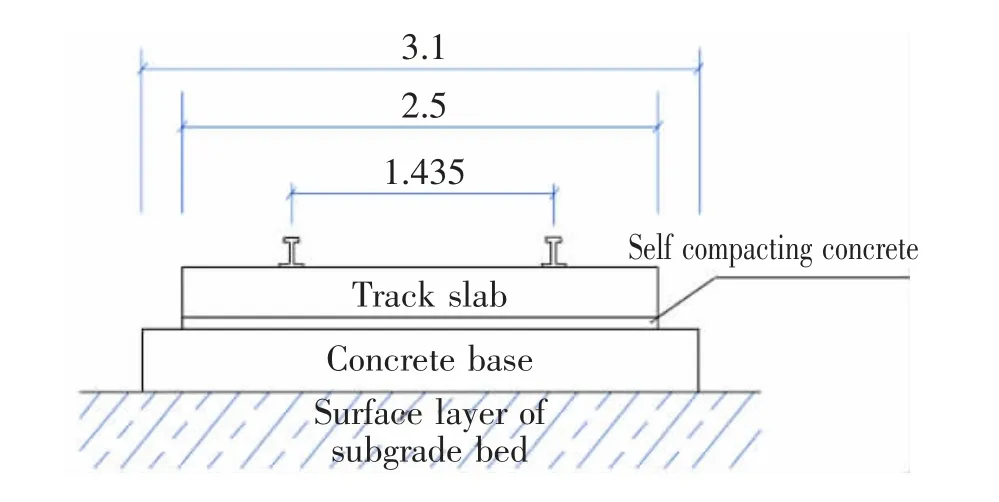
图2 CRTS III 型板式无砟轨道（单位：m）Fig.2 CRTS III slab ballastless track (Unit: m)

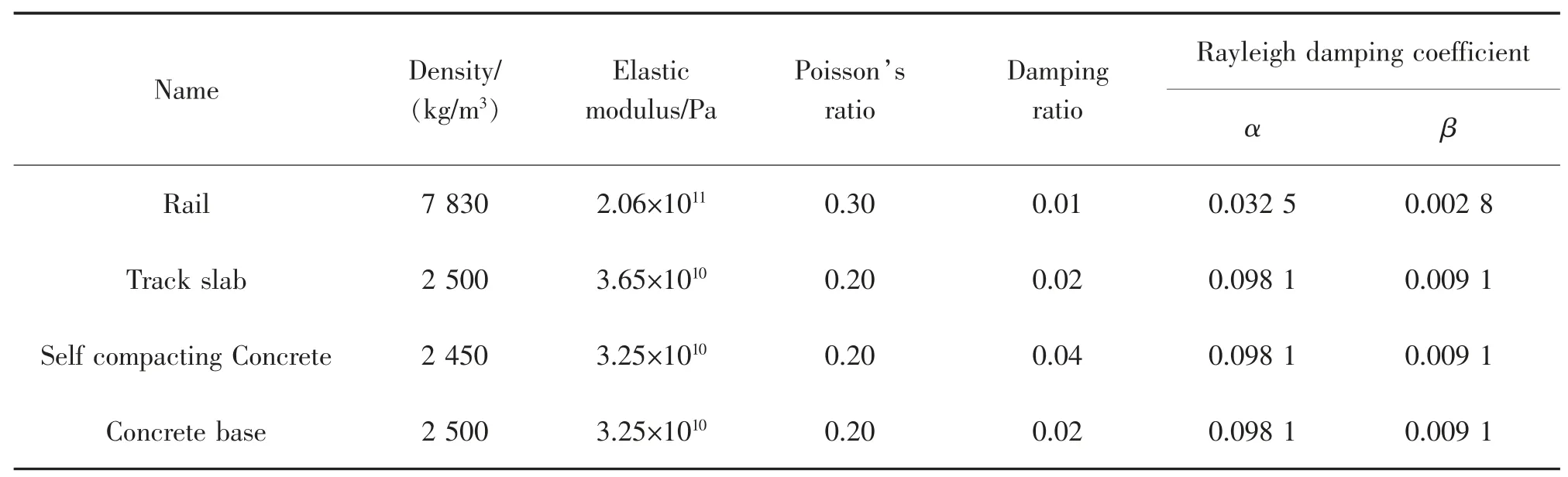
表1 轨道系统材料参数Tab.1 Material parameters of track system

1.2.2 路基土体和天然地基土

路基采用Drucker-Prager 弹塑性本构模型，同时考虑到材料的硬化，研究表明[12]交通荷载作用下地基土动应变一般小于10-5m， 故对地基土进行简化处理，考虑为弹性本构，各参数见表2[12]。由于路基土体各结构层之间错动很小， 可近似认为变形是连续的，各结构层间考虑为TIE 连接。 各结构层单元采用共节点方式进行连接， 路基两端及地基土四周通过设置等效三维一致粘弹性人工边界， 以消除截取边界尺寸造成波的反射对计算结果的影响。

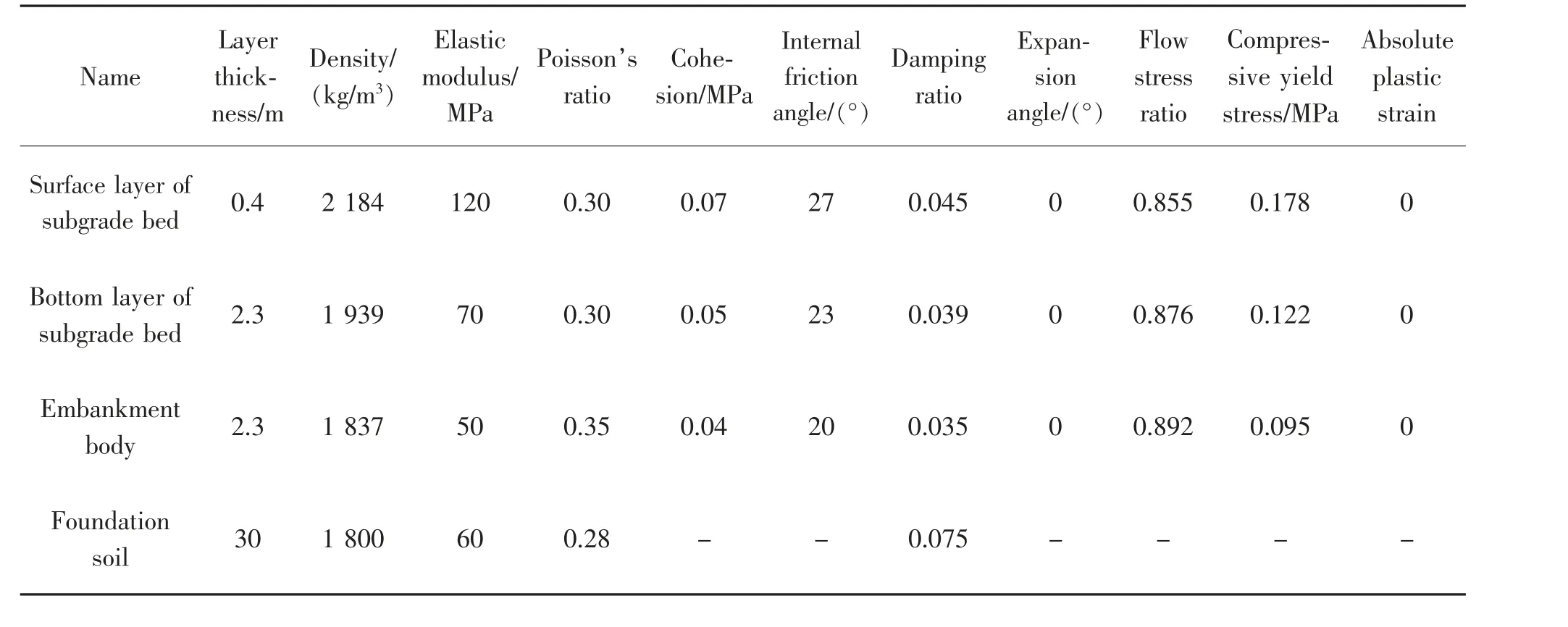
表2 路基及地基土材料参数Tab.2 Material parameters of subgrade and foundation soil

1.3 荷载计算与边界条件

1.3.1 荷载计算

基于车辆-轨道耦合动力学理论利用UM 建立列车-轨道垂向耦合模型， 车辆模型采用我国CRH3 型高速列车，具体参数见表3。 车轮踏面类型为LMA，钢轨采用60 kg/m 的轨道结构形式，在UM软件自带接口通过快速傅里叶逆变换IFFT 方法将轨道不平顺功率谱[13]转换为时域函数。 在后处理仿真阶段采用赫兹接触模型模拟轮轨接触，得到基于中国高速铁路轨道不平顺谱下的轮轨激励时程数据。 图3 为列车荷载施加示意图[11]。 轮轨垂向力如图4 所示。 在做轨道路基动力分析时，首要问题是基于轨道随机不平顺条件下如何实现对移动荷载的模拟，采用的方法是通过对有限元软件ABAQUS进行二次开发， 使用Fortran 语言编写荷载子程序VDLOAD，通过子程序将上述轮轨载荷数据加载至轨道路基模型，施加的轮轨载荷在空间上与高速列车轮轨位置相对应。 研究表明[11，14-15]：2 节车辆模型比单节车辆模型能更精确地考虑到轮对之间的叠加效应，同时在满足计算精度的前提下，比4 节车辆模型或全列车车辆模型更加节省计算时间成本。故本文模型采取2 节动车组8 轮对模型进行计算。

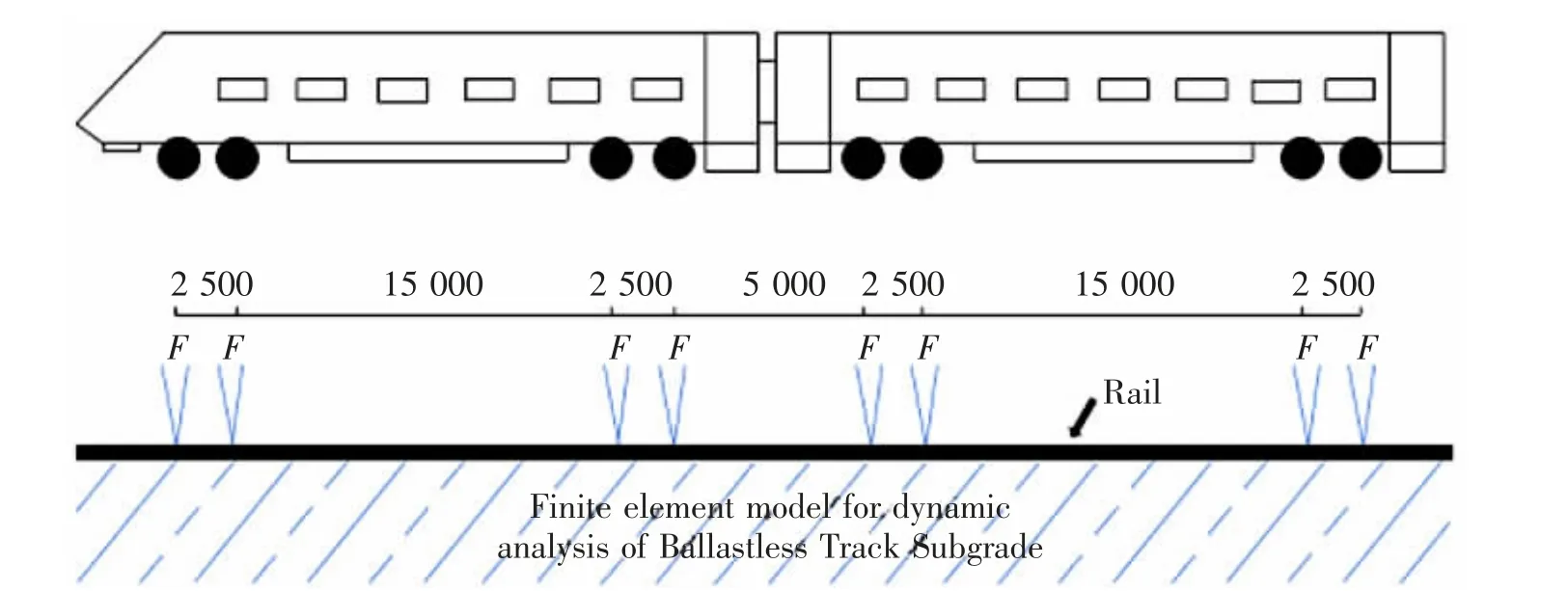
图3 列车荷载施加示意图（单位：mm）Fig.3 The applied loads (Unit: mm)

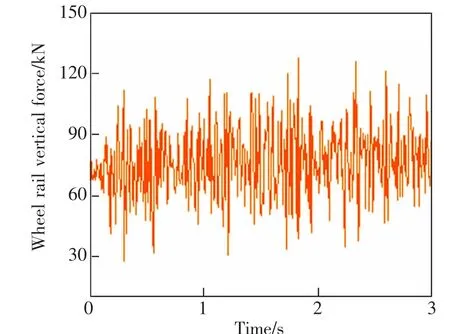
图4 轮轨垂向力Fig.4 Wheel-rail vertical force

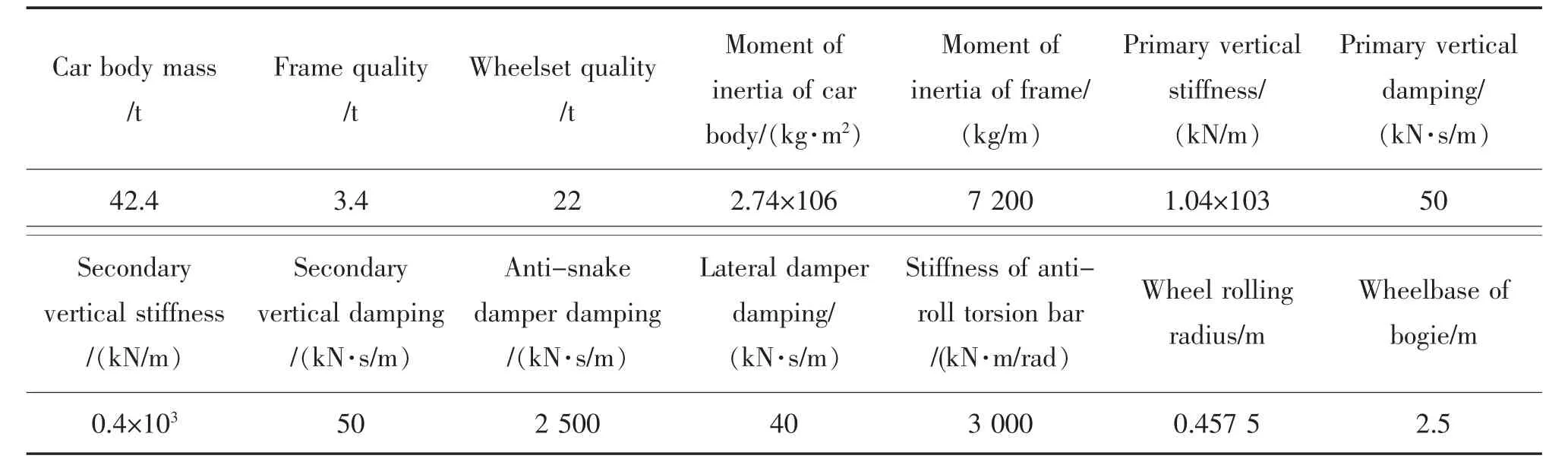
表3 高速列车参数Tab.3 High-speed train parameters

1.3.2 边界条件

在涉及地基土这种半空间无限区域的动力分析中， 直接截断地基土边界会使波在边界面上反弹，从而产生误差，本文模型路基两端及天然地基土四周采用清华大学谷音，刘晶波等[16]提出的等效三维一致粘弹性人工边界，其实质是通过在路基两端及天然地基土四周设置一层实体单元来等效替代弹簧-阻尼单元的方法吸收能量， 模拟波在半空间无限区域的传播，可较好地解决波在人工边界反射的问题，满足本文动力分析的精度需要。

2 数值分析结果

2.1 竖向动位移时程曲线

无砟轨道单线路堤标准横断面，各结构层自上而下分别为：轨道板，自密实混凝土，混凝土底座，路基及天然地基土等。 提取路基及地基土各结构层顶面的竖向动位移时程曲线， 如图5 所示。 由图5可知， 竖向动位移时程曲线具有明显的峰值规律，随着列车的驶近和驶离，伴随着监测点竖向动位移峰值的产生和消失。 在路基基床可以看到4 个峰值，对应了动车模型的4 位转向架，随着路基深度的增加，峰值数目由4 个减为3 个，这是由于中间邻近的两位转向架距离较近，产生的峰值进行了叠加。 且由图5 可以明显的看出，两位相邻转向架经过监测点上方时，后一位转向架下方的动位移幅值更大，这是由于产生的叠加效应所致。

图5 路基及地基土体各结构层顶面竖向动位移时程Fig.5 Time history of vertical dynamic displacement of top surface of each structural layer of subgrade and foundation soil

2.2 竖向动位移沿各结构层横向分布

提取路基各结构层的竖向动位移沿横向分布曲线，如图6 所示。 可以看到，在混凝土支撑层范围内，路基结构层动位移横向分布的差异较小，最大差值仅为0.129 mm，在混凝土支撑层范围外，路基结构层动位移横向分布的差异较大， 最大差值达0.701 mm。 且基床表层顶面及基床表层底面的动位移分布规律十分相似，且数值相差很小，这是因为基床表层的厚度较小，仅为0.4 m。

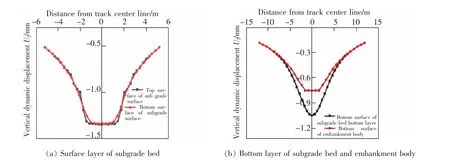
图6 路基竖向动位移幅值横向分布曲线Fig.6 Vertical dynamic displacement of subgrade in transverse direction

2.3 竖向动位移沿路基深度方向分布

竖向动位移沿路基的深度分布及衰减规律如图7 和图8 所示。 随着深度的增加，竖向动位移逐渐减小，曲线近似线性衰减，最大值位于基床表层顶面，在不同深度处轨道中心线下方的动位移幅值最大，钢轨下方的次之，混凝土底座边缘下方的动位移幅值最小，动位移量为1.350 mm，远小于我国高速铁路现行标准控制值3.5 mm。说明本文采用的路基土体符合高速铁路运行标准，满足要求。 越接近路堤本体底面，这3 条路径下的竖向动位移幅值差异越小。 这是因为随着深度的增加，由上部结构传递下来的动力响应经过路基各层吸收和再分配，在到达路堤本体底面时，动位移幅值沿横向分布的差异变小。

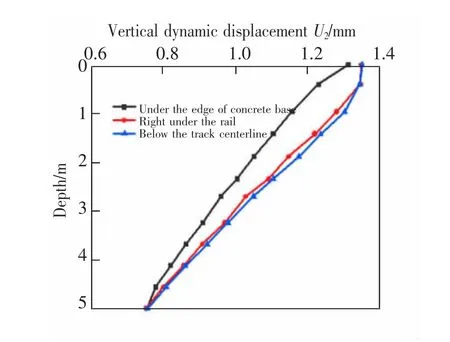
图7 竖向动位移沿深度分布曲线Fig.7 Vertical dynamic displacement distribution along the depth direction

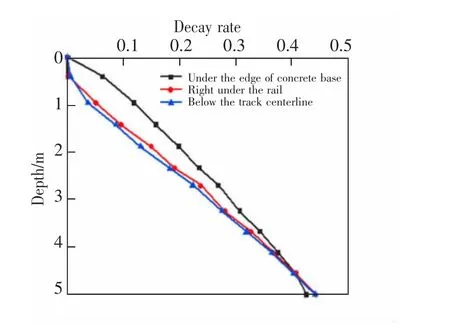
图8 竖向动位移沿深度衰减规律Fig.8 Vertical dynamic displacement attenuation law along the depth direction

2.4 参数分析

表4 和表5 为列车在不同路基基床刚度、地基土刚度和列车时速下路基基床各结构层的竖向动位移幅值曲线，为了更形象直观地描述不同参数对竖向动位移幅值的影响， 同时结合图9 来共同说明。由图表可知，基床表层弹性模量在120～210 MPa，基床表层、基床底层及路堤本体的竖向动位移幅值均随着弹性模量的增大而减小，但各结构层动位移减幅均不超过3%，对动位移的影响作用较为有限。基床底层弹性模量在70～160 MPa，基床表层、基床底层及路堤本体的竖向动位移幅值均随着弹性模量的增大而减小，且在基床表层和基床底层的动位移减幅更加明显，最大减幅达17.13%，相较于基床表层弹性模量变化的影响，基床底层的影响更加显著。 地基土弹性模量在20～80 MPa，自上而下路基各结构层面的动位移均有不同程度的降低， 其中基床表层顶面， 底面的竖向动位移分别减小了32.77%，33.19%，基床底层底面和路堤本体底面则分别减小了40.89%和48.86%。 可以看出地基土弹性模量的变化对动位移的影响十分显著，对降低路基动位移具有较大积极意义。速度在200～350 km/h范围内，随着列车移动速度的增加，动位移幅值呈逐渐增大趋势。其中，基床表层顶面动位移幅值对速度变化最敏感，速度由200 km/h 增大至350 km/h，动位移幅值增长了49.60%，由上至下其他路基结构层动应力幅值分别增长了33.55%，36.40%，39.98%。列车时速对路基结构的位移变形有显著的影响，在实际高速铁路运行中要合理设定列车行驶速度。

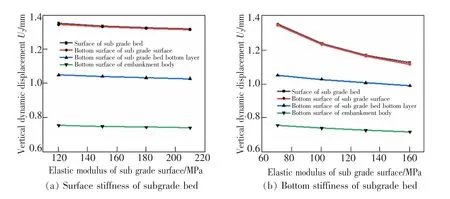
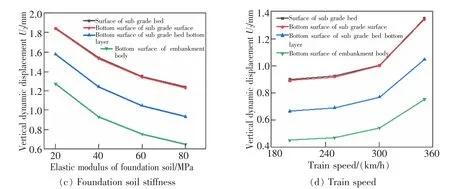
图9 影响竖向动位移的参数分析Fig.9 Analysis of parameters affecting vertical dynamic displacement

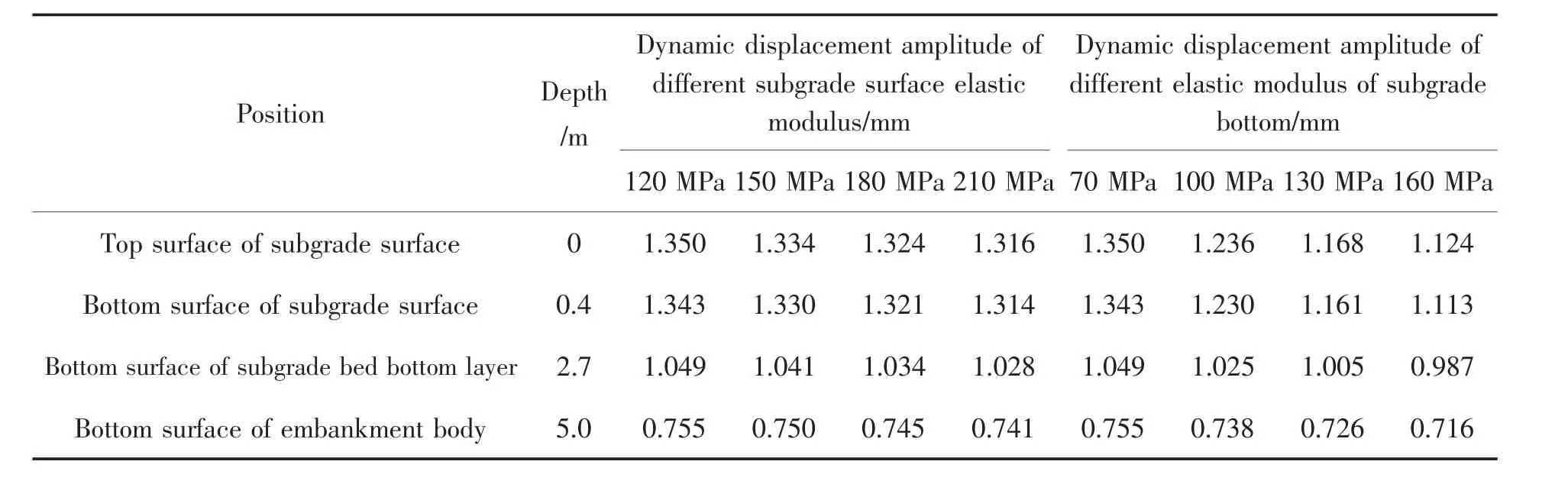
表4 路基基床刚度对路基动位移的影响Tab.4 Influence of subgrade bed stiffness on dynamic displacement of subgrade

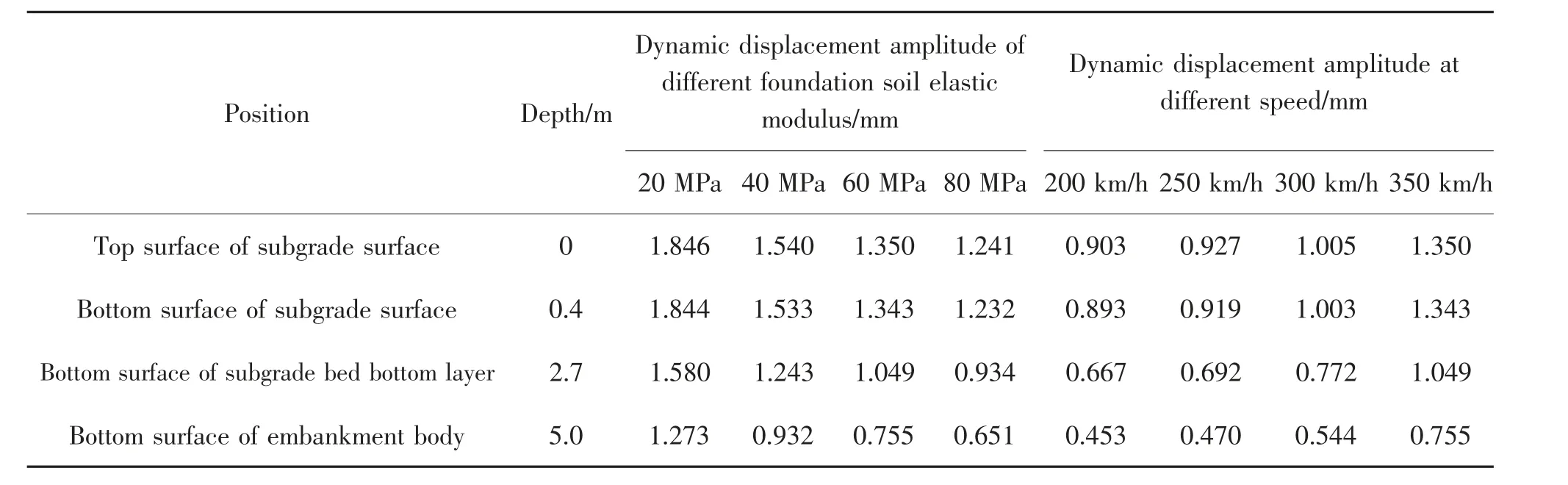
表5 地基土刚度和列车时速对路基动位移的影响Tab.5 Influence of foundation soil stiffness and train speed on dynamic displacement of subgrade

3 结论

本文建立了三维有限元CRTS III 无砟轨道-路基-土体模型，通过数值分析计算得到了如下结论：

1） 采用的有限元模型计算得到的路基竖向动位移远小于我国现行高速铁路标准的控制值3.5 mm，满足要求。列车模型为2 节动车，中间两组轮对移动产生的动位移叠加，竖向动位移在各结构层中的时程曲线峰值与转向架数目进行对应。

2） 由于转向架二次作用产生的叠加效应，两个相邻的转向架经过时后一个转向架经过时的动位移幅值明显大于前一个转向架经过时的动位移幅值。 沿横向分布，在混凝土底座范围内，路基各结构层竖向动位移幅值沿横向分布变化较小，各结构层横向最大差值仅为0.129 mm； 在混凝土底座范围外，路基各结构层竖向动位移幅值横向分布差异较大，横向最大差值均超过0.5 mm。 竖向动位移在路基中随着深度的增加逐渐衰减，最大值位于基床表层顶面，近似线性衰减。

3） 基床表层弹性模量的变化对系统动力响应影响作用较有限；基床底层弹性模量的增大对降低路基中的动位移影响作用较显著，有利于行车运行的平稳、舒适及安全。 地基土弹性模量的变化对路基中对降低系统动位移的作用最显著。 提高列车时速会加大路基的变形位移，应根据具体线路实际运营情况合理控制列车运行速度。