存在扰动和时滞的高速列车自适应制动控制

谭 畅，李毅清， 杨 辉

（1. 华东交通大学电气与自动化工程学院，江西 南昌 330013;2. 华东交通大学江西省先进控制与优化重点实验室，江西 南昌 330013）

铁路系统是攸关旅客生命及财产安全的大型地面运输系统。 近年来，高速列车发展尤为迅速，已成为广大群众外出远行的重要交通工具，其安全运行至关重要[1-3]。 列车制动系统的性能是实现运行安全的前提和基础，提高高速列车的制动性能，保障列车安全、平稳运行日益成为各国研究高铁的焦点问题[4]。 研究高速列车制动过程的建模与控制，对提高列车的制动性能和运行安全性具有重要的现实意义。

当前，主要研究方向是高速列车制动过程的建模和控制。 针对高速列车制动过程中的建模问题，师黎[5]基于动力学分析，建立了高速列车制动过程中的机理模型。 该模型假定列车制动时基本阻力恒定， 在建模精度上与列车实际的制动模型存在差异。 袁海军等[6]通过单质点模型建立了特征模型，提出了最优PID 控制器。 连文博等[7]在单质点模型的基础上建立了高速列车的状态空间方程，通过对传统PID 控制器的改进， 设计了自抗扰控制器。 刘晓宇等[8]通过分析高速列车具体的制动控制过程，建立了传递函数模型，该模型反映了列车制动控制力产生的动态过程。 Liu 等[9]和Tong 等[10]将非线性模型表示为T-S 模糊模型， 并基于状态观测器及自适应、 鲁棒等策略设计了分布式模糊控制器。

针对高速列车制动过程中的控制问题，Mao 等[11]考虑了高速列车的时变系统参数和未建模干扰，提出了对时变参数进行参数化的方法，设计了自适应故障补偿器。耿睿等[12]通过分析列车的牵引-制动系统，考虑到列车运行过程中空气阻力、未知干扰等非线性因素，将实际输出与线性模型输出的误差描述为未建模动态，设计了多变量非线性广义预测控制器。 罗恒钰等[13]构建基于增广误差的自适应控制系统，实现了制动系统的速度跟踪控制。 当前控制器设计很大程度上依赖参数已知的模型。 自适应控制善于解决参数未知系统，本文针对参数未知的系统，采用模型参考自适应控制（MRAC）策略进行高速列车制动控制。

此外，由于延时会影响列车安全运行，当前已有研究人员针对时滞系统进行了相关研究。 Zhou等[14]针对具有未知时滞和输入饱和的非线性系统，采用模糊逻辑方法逼近系统的未知函数解决自适应输出跟踪控制问题。 Xi 等[15]研究了具有不匹配非结构非线性和未知时滞的高阶严格反馈系统的自适应渐近跟踪控制问题，利用自适应机制和投影算子估计未知时滞。罗仁士等[16]基于Pade 和自适应方法处理制动模型中的时滞及外部扰动。 目前多数学者在处理延时问题时将延时近似处理，忽略其所带来的影响，因此处理列车制动延时问题十分有必要。

列车在实际制动过程中存在一定的干扰，在此方面国内外学者已进行了相关的研究。 刘晓宇[17]通过分析高速列车停车控制过程，在外部阻力干扰已知的情况下，将MPC 引入到列车停车控制问题中，设计了高速列车精确停车预测控制算法。张梦楠等[18]基于Krasovskii 泛函算子，设计了鲁棒制动控制器，以消除模型中非线性、 时滞及有界扰动的影响，并分析了系统的稳定性。

本文充分利用模型参考自适应控制处理系统不确定性和外界扰动的能力，设计了新的高速列车制动系统自适应控制策略，使其在存在未知扰动和输入延时的情况下，仍能保证系统稳定和实现对给定速度曲线的渐近跟踪， 保障高速列车的安全、可靠运行。

1 问题提出

为了使高速列车制动系统在存在扰动和时滞的情况下仍能保持系统稳定和实现对给定速度曲线的渐近跟踪，本文充分运用模型参考自适应控制方法的优势，研究其建模和控制问题。 本节首先通过分析高速列车制动系统的原理和动态特性，建立存在扰动和时滞的高速列车制动系统状态空间模型，并提出其自适应控制问题。

1.1 存在扰动和时滞的高速列车制动系统模型

为了建立高速列车在存在扰动和时滞情况下的制动系统模型，首先对其制动系统原理和动态特性进行分析。

高速列车的制动指令不直接作用于其动力执行单元，而是通过微制动控制单元（MBCU）接收司机或者列车自动驾驶子系统（ATO）发出的制动信号，并结合车辆的载重量和车速等信息，计算所需的制动力及减速度，从而实现对高速列车运行状态的控制。 根据制动系统原理，可将高速列车制动系统表示为图1。 图1 中，m 为载重量，kg； u（t）为制动力指令，N；τ 为高速列车延时时间， 也称为空走时间，s； u（t-τ）为存在延时的制动力指令；v（t）为高速列车的实际速度，km/h；a（t）为高速列车的实际制动减速度，m/s2。 此外，在列车运行过程中由于受到外界扰动会对实际的制动减速度产生影响。

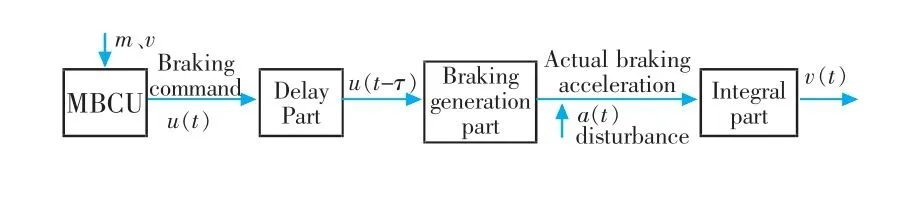
图1 列车制动系统示意图Fig.1 Schematic diagram of braking system of train

根据高速列车制动系统原理，可将制动过程大体分为接收信号、延时、制动力生成、扰动和积分5个环节。

1） 接收信号环节。高速列车的制动过程首先由MBCU 接收司机或ATO 发出的制动信号，并计算当前所需的制动力u（t）。

2） 延时环节。 因为信号传输和机械传导等原因，MBCU 计算的制动力指令u（t）需经过一定的延时才能作用于执行机构。 将延时环节表示为

其中：τ 为延时时间，s；u1（t）存在延时的制动力指令，N。

注释1：在实际制动系统中，无论是电气制动装置还是空气制动装置，均存在延时环节[4]。

3） 制动力生成环节。 高速列车的制动力u1（t）与其产生的a1（t）的关系可近似为线性关系[2]，基于比例系数K 将其描述为

制动控制装置通过“反馈”作用实现实际制动减速度a（t）与目标制动减速度a1（t）的跟踪控制[19]，动态过程由一阶惯性环节表示

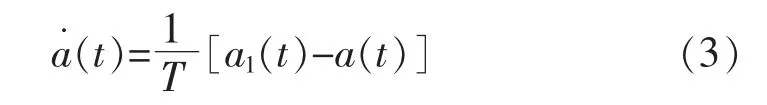
其中：T 为制动系统时间常数。

4） 扰动环节。 高速列车在制动过程中，受到外界扰动影响，将对减速度产生影响。 为了进行高速列车制动系统建模与控制研究，我们将外界扰动d（t）表示为

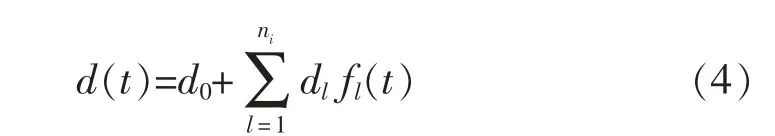
其中：d0和dl为未知常数；fl（t）为已知基函数；ni为基函数的个数。 可以通过选取适当形式和个数的基函数fl（t）逼近实际扰动，当ni足够大时，扰动模型可以逼近任何实际的外界扰动。

此时，实际制动减速度a2（t）表示为如下形式

5） 积分环节。高速列车的实际速度v（t）由其实际制动减速度a2（t）通过积分环节得到

根据上述分析， 可将高速列车制动系统模型框图表示为图2。 图2 中，T 为制动系统时间常数；s 为拉氏变换算子；u（t）为制动力指令，N；τ为列车延时时间，也称为空走时间，s；u1（t）为延时后的制动力指令，N；K 为比例系数；a1（t）为目标加速度，m/s2；a（t）为控制加 速度，m/s2；d（t）表示由于受到干扰而使高速列车产生的附加加速度，m/s2；a2（t）为实际制动加速度，m/s2；v（t）为列车实际速度，km/h。

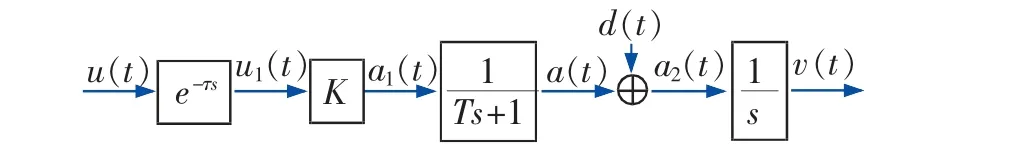
图2 高速动车组制动系统模型框图Fig.2 Model diagram of braking system for high-speed EMU

根据式（1）～式（5）得到存在扰动和延时的高速列车制动系统动力学模型为

定义状态变量：x=［x1，x2］T=［v，a］T，则存在扰动和延时的高速列车制动系统状态空间模型为

1.2 高速列车制动系统自适应控制问题

鉴于自适应控制在处理系统不确定性的优势，考虑到高速列车运行环境复杂多变，且制动系统存在大量不确定性和扰动，本文针对存在扰动和时滞的高速列车制动系统（8），采用模型参考自适应方法设计制动控制器，实现其对给定速度曲线的渐近跟踪，以保障高速列车的安全正点运行。

因此，本文的控制目标为：基于模型参考自适应方法设计状态反馈状态跟踪高速列车制动控制器u（t），保证所有闭环信号有界，且其速度和加速度x（t）渐近地跟踪给定的信号xm（t）=［vm，am］T。

2 自适应制动控制器设计

为了实现1.2 节中提出的控制目标， 本文设计的高速列车模型参考自适应控制系统框图如图3所示。 高速列车自适应制动控制器的设计步骤为：首先根据系统特性和控制目标选取稳定的参考模型xm（t）；其次基于匹配方程对高速列车制动系统模型进行系统参数化，并基于参数化模型，设计标称控制器； 最后基于标称控制器设计自适应控制器，作用于存在扰动和延时的高速列车制动控制系统。

图3 高速列车模型参考自适应控制系统框图Fig.3 MRAC diagram of high-speed train

2.1 参考模型

为了设计高速列车制动系统模型参考自适应控制器，首先应选择适合的参考模型。 本文根据熟练司机的驾驶经验得到给定的速度曲线作为参考模型的输出，即xm（t）=［vm，am］T，并根据控制目标和制动系统结构，选择稳定的参考模型

注释2：与传统的模型参考自适应方法首先选择有界的外部输入信号r（t），再根据式（10）得到参考模型的输出xm（t）不同，本文基于给定参考模型的输出xm（t）（即给定的速度曲线）和选定的参考模型系统矩阵（Am，Bm），根据式（10）计算得到外部输入信号r（t），并将其作为制动控制信号的一部分，将给定速度曲线信息用于控制器设计。

2.2 系统参数化

为了设计状态反馈控制器u（t），使x（t）渐近地跟踪参考模型的输出xm（t），须满足如下匹配方程。

2.3 状态预测

由于高速列车制动控制器（17）中含有未来的状态变量x（t+τ），因此需使用状态预测的方法对状态x（t+τ）进行预测。

引理1[20]考虑连续时间线性时不变系统x˙=Ax+Bu，其状态运动规律为同时作用有初始状态和输入的状态方程的解，具体表达式为

根据式（18）以及黎曼积分法，通过变量替换可求解x（t+τ），即

2.4 标称控制器

标称控制器为系统参数已知的情况下，为实现期望的控制目标设计的控制器，因此本文设计的高速列车制动系统标称控制器为

2.5 自适应控制器

虽然标称控制器可使闭环系统具有理想的系

2.6 稳定性分析

本文设计的存在时滞和未知扰动的高速列车自适应制动控制系统有如下系统性能。

3 仿真验证

为了验证本文设计的存在扰动和时滞的高速列车制动系统自适应控制器的有效性， 本节以CRH380AL 型高速列车制动系统为被控对象进行仿真实验研究。

3.1 仿真实验数据

我们首先采集济南—青岛段CRH380AL 型高速列车制动过程的360 组真实速度数据 （单位为km/h）进行曲线拟合，得到给定的速度曲线（见图4中的目标速度曲线）。

3.2 仿真实验结果

基于3.1 中选定的设计数据， 根据第2 节中的设计过程， 设计高速列车自适应制动控制系统，进行仿真实验。 实验得到的仿真结果如图4～图6 所示，分别为高速列车制动系统速度、加速度位移跟踪曲线和误差曲线。

图4 列车速度跟踪及误差Fig.4 Train speed tracking and error

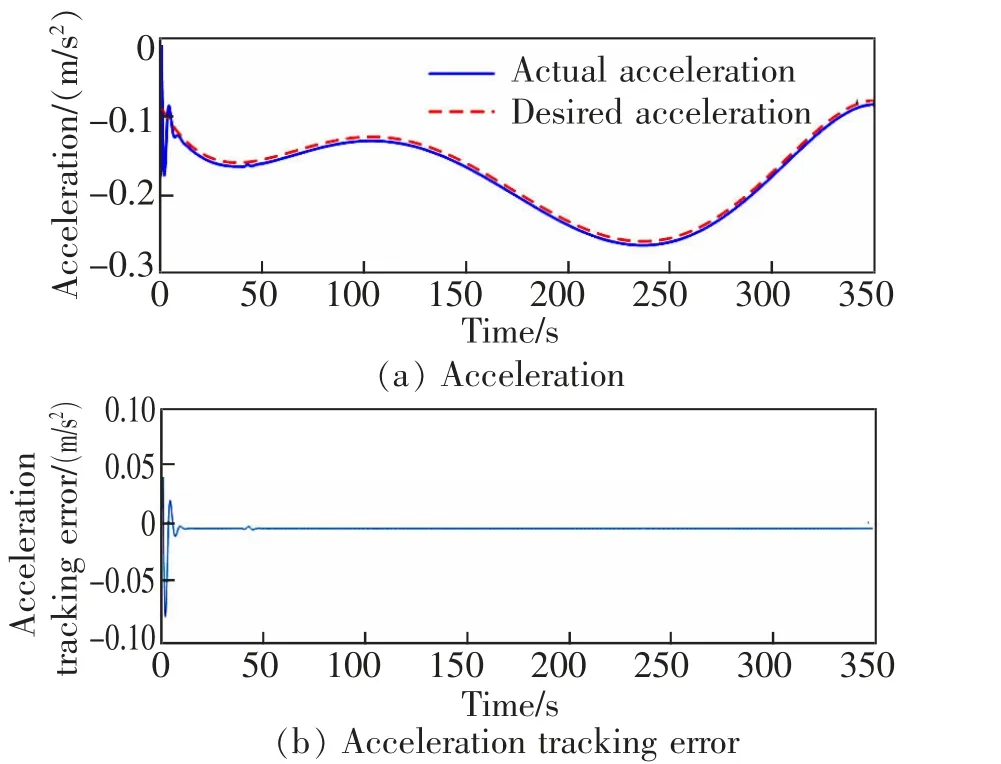
图5 列车加速度跟踪及误差Fig.5 Train acceleration tracking and error

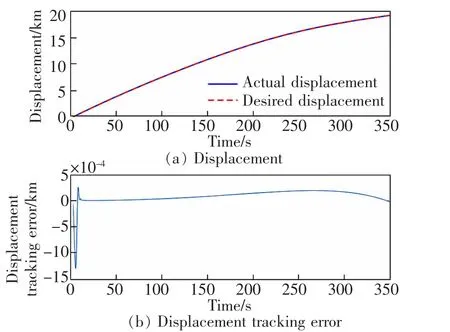
图6 列车位移跟踪及误差Fig.6 Train displacement tracking and error

由图4～图6 可知，虽然制动系统存在时滞和未知扰动，但本文设计的高速列车制动系统自适应控制器仍能保证所有闭环信号有界，速度、位移和加速度最大跟踪误差分别为0.3 km/h，1.29 m 和0.09 m/s2，均在系统运行的范围内，且在15 s 内实现了速度和加速度误差渐近收敛于原点附近的邻域，位移误差趋近于0，实现了控制目标，且跟踪精度高，系统的制动性能理想。 此外，通过仿真图5 可知，列车制动加速度曲线平缓，变化缓慢，保障了列车的安全制动，也提高了列车制动时的平稳性。 由此可见，该控制器能够克服未知参数和有界扰动的影响， 虽然速度和加速度存在一定的稳态误差，但跟踪的精度较高，系统的制动性能较理想，该控制器的鲁棒性较强。

4 结论

本文以存在未知扰动和已知时滞的高速列车制动过程为研究对象， 研究了其建模和控制方法，得出以下结论：

1） 对于存在已知时滞的高速列车制动过程，基于模型参考自适应控制方法设计的制动控制器能保证系统稳定， 实现对给定速度曲线的渐近跟踪，从而保障高速列车的安全可靠运行。

2） 在系统存在外界干扰和未知系统参数，该控制器能够克服未知参数和有界扰动的影响，具有良好的鲁棒性。

3） 本文设计的控制系统考虑了扰动、延时等环节，提高了高速列车制动模型的精度，且制动性能较理性，制动过程平稳性强，确保了高速列车安全可靠平稳运行。