基于声子晶体理论的轨道交通减振降噪研究综述

冯青松，梁玉雄，陆建飞

（1. 华东交通大学铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013;2. 江苏大学土木工程与力学学院，江苏 镇江 212013）

随着列车运行速度的提高，列车与轨下结构的动态相互作用显著加剧，带来的振动与噪声问题日益突出，如钢轨波浪型磨耗问题[1]，钢轨扣件弹条断裂问题，无砟轨道混凝土结构在反复列车动荷载作用下出现的裂纹、离缝、剥离掉块问题[2-3]，以及噪声问题[4]等，不仅影响轨下结构的健康状况和使用寿命，而且影响列车运行的安全性及舒适性。 铁路中的多跨周期性桥梁、盾构管片隧道、轨道结构均可作为声子晶体结构对其振动问题进行研究，其中桥梁以梁长为周期， 盾构管片隧道以管片长度为周期，钢轨以扣件支撑间距为周期，轨道板以其长度为周期，这就使得采用声子晶体理论分析其能带结构、传输特性等固有振动特性和振动响应特性成为可能。 声子晶体（phononic crystals）是凝聚态物理领域在光子晶体（photonic crystals）研究的基础上提出的一个新的物理概念[5]。 声子晶体是指由2种或2种以上介质组成的具有弹性波带隙特性的周期性复合材料或结构，弹性波在声子晶体中传播时，某些频率范围内的弹性波不能传播，相应的频率范围称为带隙（也称禁带）；而其他频率范围内的弹性波可以传播，相应的频率范围称为通带[5-7]。 声子晶体理论的减振降噪在舰船类、航空类、汽车类等精密机械制造领域有一些应用尝试。 在土木与交通工程领域，声子晶体理论在地基基础隔振、交通环境振动的地基排桩隔振、 简单的周期支撑桥梁振动分析等方面有一些初步成果[8]，且主要针对低频范围的振动。 由于声子晶体结构可看作由特殊设计的人工结构单元周期排列构成的新材料/结构， 通过调节人工周期结构的几何/材料参数， 可以人为调控带隙的位置、宽度及其对波传播的抑制能力。 这为轨道交通减振降噪带来了一种新的思路： 利用轨道交通中的周期性结构， 或将减隔振构造和声屏障等设计成为特殊的声子晶体结构， 利用带隙特性调控弹性波传播实现减振降噪的目的。 因此近年来， 越来越多的学者从声子晶体结构中弹性波传播角度对针对轨道交通振动问题进行研究，为弹性波传播角度对振动控制提供理论依据和应用技术研发的基础。

1 声子晶体理论带隙控制原理

1992年Sigalas等[8]首次从理论上证实了球形散射体埋入某一基体材料中形成的三维周期点阵结构中存在弹性波带隙。 1993年Kushwaha等[9]在研究由镍-铝组成的二维周期结构时， 针对弹性波首次提出声子晶体的概念，并首次指出声子晶体带隙特性在高精密无振动环境方面具有潜在的应用前景。 根据周期性的空间维数声子晶体可分为一维、二维、三维声子晶体（如图1所示）。

图1 声子晶体周期性维数分类Fig.1 The classification of phononic crystals by the periodic dimension

关于声子晶体弹性波带隙形成的机理比较成熟的可分为2类，分别是Bragg散射机理（bragg scattering）和局域共振机理（local resonance）[10]。 Bragg散射机理中带隙的出现频率位置主要受Bragg条件控制，即

式中：a为声子晶体的晶格尺寸（周期结构的最小周期尺寸）；λ为声子晶体中的弹性波波长。 Bragg带隙的本质是结构周期性对波传播的影响， 晶格结构、尺寸及材料组份搭配均是带隙设计的关键因素，带隙对应的波长与晶格尺寸数量级相当，在减振设计时带来了晶格尺寸的一定限制。

2000年，Liu等[11]首次提出了声子晶体产生带隙的另一种机理——局域共振机理（local resonance）。局域共振带隙频率对应的波长远远大于晶格尺寸，即远远突破了Bragg条件的限制。局域共振型声子晶体元胞（单个周期）可简化为由质量和弹簧组成的简化系统，通过简化系统的共振模式和固有频率来估计局域共振带隙的起止频率，带隙的产生机制受局域共振单元自身的谐振特性和基体中长波行波的相互作用影响。

声子晶体结构弹性波带隙计算方法有传递矩阵法、平面波展开法、时域有限差分法、多重散射法和有限单元法，除了以上几种常见方法以外，目前其它一些研究方法也逐渐被尝试用于周期结构带隙的计算中，如集中质量法[12-14]、变分法[15]、谱单元法[16]、小波分析法[17-18]和改进的能量法[19]等。

声子晶体结构中弹性波传播特性的研究已经有了一定的基础，并在理论和实验上均已对带隙在减振降噪方面潜在的应用前景进行了验证。 国防科学技术大学温熙森，温激鸿等[10]系统地将声子晶体带隙原理引入典型机械结构减振降噪设计中，实现了利用人工周期结构带隙特性控制结构中振动波的传播，在带隙算法、机理分析、优化设计、 减振降噪应用探索等方面取得了重要进展，如研究了声子晶体梁板类结构的振动带隙特性， 流固耦合声子晶体管壳结构的带隙特性等。Koo 和Park[20]通过实验验证了周期支撑管梁系统中弯曲振动带隙的存在，通过改变周期支撑的位置可以抑制某些频段内的波在结构中的传播。Singh等[21]通过研究周期压电杆和周期压电梁证明了利用压电材料改善周期结构的禁带特性的可行性。 朱宏平[22]通过研究单耦合或多耦合带横梁的周期柱结构，验证了利用带隙特性可以在较宽的频率范围内控制周期柱结构的振动。 Faiz等[23]利用三维打印技术设计并制造了一种由圆柱形柱组成的方形声子晶体金属器件， 利用有限元法、微系统分析仪（MSA）和多普勒激光扫描仪，证实了0.3 MHz左右的兰姆波的完整带隙， 以及通过插入空间带隙在声子晶体内实现声波的定向传输效果。

通过布拉格带隙和局域共振带隙的耦合和转化，为通过实现带隙的位置和宽度控制用于轨道交通减振降噪带来了新的实现途径和思路。

2 基于声子晶体的轨道交通振动分析

2.1 周期轨道振动分析

针对轨道结构的周期性支撑特点，不少学者从声子晶体理论中弹性波传播角度进行了研究，声子晶体理论分析模型从单层支承梁到多层支承梁模型， 并对阻尼和周期失谐也进行了一定的研究。Sheng等[24]建立了周期性支撑的欧拉梁模型，分析了轨道结构的频散特性及共振特性；Wang[25-26]利用声子晶体理论通过欧拉梁模型分析了不考虑阻尼时有砟轨道结构带隙行为和形成机制，并通过铁木辛柯梁模型和现场测试研究了不考虑阻尼时有序和随机无序高铁无砟轨道中的波传播问题。 易强[27]将钢轨考虑为铁木辛柯梁建立了声子晶体理论分析模型， 研究了弹性波在周期性轨道结构中传播特性，发现在带隙范围内弹性波在轨道结构中无法自由传播，且外界激励也无法向系统输入能量。 冯青松等[28]将有砟轨道结构简化为周期离散支承钢轨和轨枕组成的双层梁声子晶体理论模型, 如图2所示,通过平面波展开法计算了周期轨道结构垂向振动带隙特性， 并以我国CRSTIII 型无砟轨道结构为例，运用人工弹簧定义周期性边界，采用改进的能量法计算了周期性组合结构弯曲振动的带隙，并与有限元结果进行了比较[19]。 上述研究体现了理论分析方法逐渐具有多样性，周期轨道中波传播特性的研究也取得的较大进展，但尚未涉及曲线段钢轨的研究。

图2 有砟轨道声子晶体理论模型Fig.2 Phononic crystal model of ballasted track

2.2 周期桥梁振动分析

在周期性桥梁的振动理论方面， 当前的研究从自由振动的固有振动特性分析，再到移动点荷载、移动质量、移动荷载列和移动车辆作用下的桥梁动力响应分析等几个方面进行。 Lu等[29-31]引入声子晶体理论，采用传递矩阵法、傅里叶变换法、有限元法等频率-波数域解析分析方法，建立了刚性支撑的周期性简支高架桥梁的计算模型,如图3所示， 得到桥梁结构自由振动的特征方程和移动点荷载、 移动质量作用下的动力响应，分析了周期性高架桥的共振和消振条件[32-34]，以及桩基础支撑缺陷周期性架桥的缺陷态，比较各跨在缺陷态频率处的响应发现波动局域于缺陷跨处[35]。范胜帅[36]将车桥作用力展开为傅里叶级数，利用单位简谐移动荷载作用下周期性高架桥的基本解，计算了周期性高架桥在移动车辆作用下的动力响应。 曹艳梅[37]采用无限周期结构理论和有限元法， 提出了任意荷载列作用下桥梁结构周期性单元受等效结点荷载时矢量频谱的计算方法，计算了高铁32 m等跨径布置高架桥的能带特性及其在不同频率轨道不平顺引发的移动简谐荷载激励下的动力响应及墩底动反力。 为了研究地震发生时列车运行状态下的周期桥梁振动响应，Chen[38]利用傅里叶变换方法和有限元方法研究了无限周期性高架桥（IPV）在运动质量和谐震波同时作用下的动态响应，数值结果表明，在运动质量和地震波的共同作用下的平面内横向位移大于由于地震波单独引起的横向位移，对于平面外的横向位移通常小于地震波的横向位移。 目前周期性桥梁振动响应研究中仍然未全面考虑桥梁-轨道耦合效应和曲线桥梁的特殊性， 移动车辆下的振动响应也未反映桥上轨道短波不平顺特性。

图3 周期性高架铁路示意图Fig.3 The illustration of the periodic elevated railway

2.3 周期隧道振动分析

为研究周期隧道中列车运行引起的振动环境影响，马龙祥［39］首次建立了用于分析的薄片有限元-无限元耦合模型，基于无限-周期结构理论的车轨耦合建立了隧道-地层振动响应分析模型， 研究了列车运行引起的轨下基础-隧道-地层系统振动响应。 在研究列车运行时周期隧道的动态响应及随机失谐产生的波动局部化现象方面，丁兰[40]基于力-位移原理的解析动态刚度矩阵法和传递矩阵法拓展至速度域，并对有限周期隧道的振动传输特性和变形情况进行了计算和仿真，得出对于谐调周期隧道，频域和速度域内通、禁带均交替出现，以及失谐周期隧道时的波动局部化现象在高频低速度区最为显著的结论。 为进一步分析不同控制参数对弯曲波动局部化特性的影响，尹涛[41-42]利用传递矩阵法将随机失谐参数引入到周期结构中,根据Wolf算法,采用局部化因子计算分析，并证明当波动频率小于该临界频率时,弯曲波的传播始终是衰减的,弹性地基作用使得周期隧道弯曲振动波的禁带频率有所提高。 为探索通过调整隧道结构尺寸参数来改变隧道中波的传播特性，鞠海燕[43]基于声子晶体理论和Flugge壳体理论, 建立了圆形隧道声子晶体模型,如图4所示， 分析了弹性模量变化和几何尺寸变化对隧道波的传播特性的影响, 结果表明长度比的变化对周期性隧道禁带的幅值、 宽度和个数影响显著。可以看出， 以上的研究更多的是针对于长直隧道、规则断面隧道及均匀地层，在轨道-隧道-地层模型复杂性和工程适用性方面仍有提升的空间。

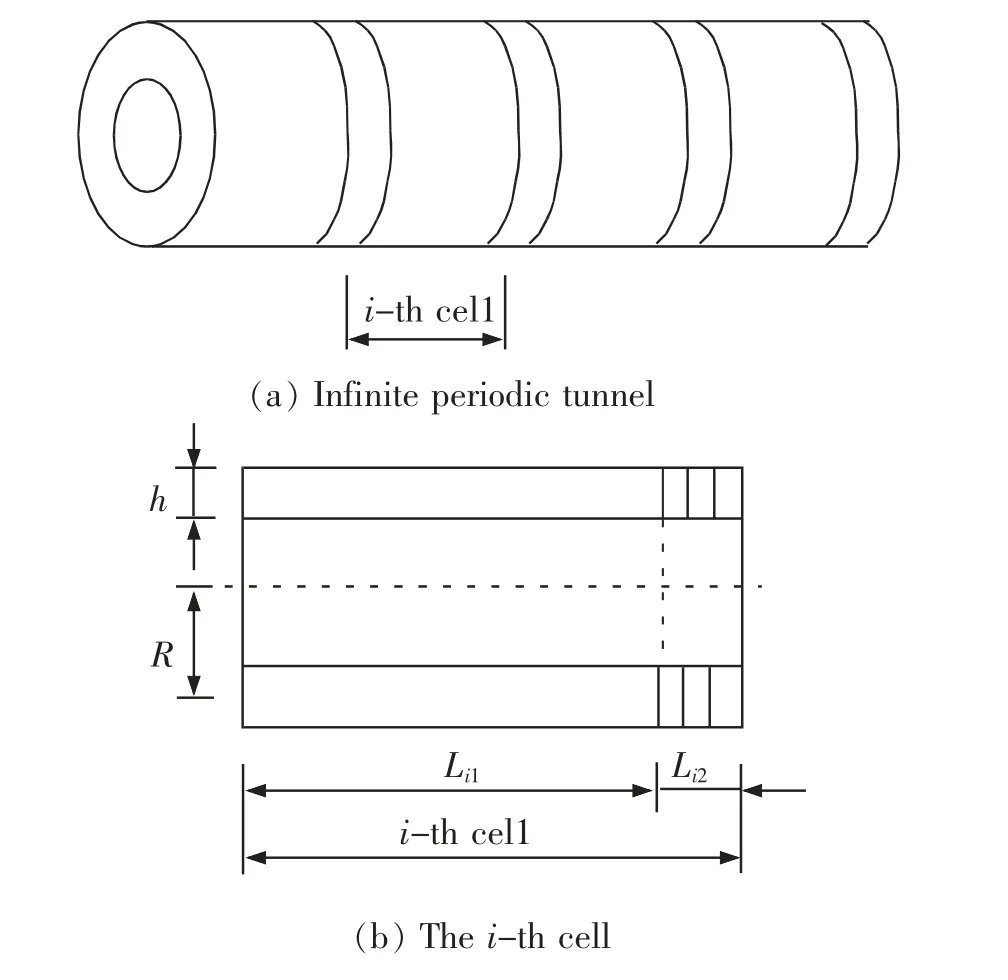
图4 周期性隧道示意图Fig.4 The illustration of the periodic tunnel

3 基于声子晶体的铁路振动控制

3.1 轨道结构减振控制

许多学者将声子晶体中波传播理论，禁带和局域化特性应用到轨道交通振动控制研究中。 传统轨道结构减振中常采用的钢轨动力吸振器符合声子晶体中局域共振机理。 孟铎[44]基于声子晶体带隙原理，从弹性波传播特性出发，采用钢轨动力吸振器进行了周期性轨道结构的振动控制研究。 邢俊[45]基于Bragg散射和局域共振机理，做了地铁轨道结构的声子晶体弹性垫层波阻单元的结构设计和材料设计及关键参数讨论分析，并对其减振效果进行了评价。 Sheng等[46]提出了一种应用在地铁浮置轨道板的局部共振声子机理的超屏障，如图5所示，抑制低频带隙频率范围内纵波从道床板往基底的传播，达到提高新型浮置板轨道的整体减振效果。

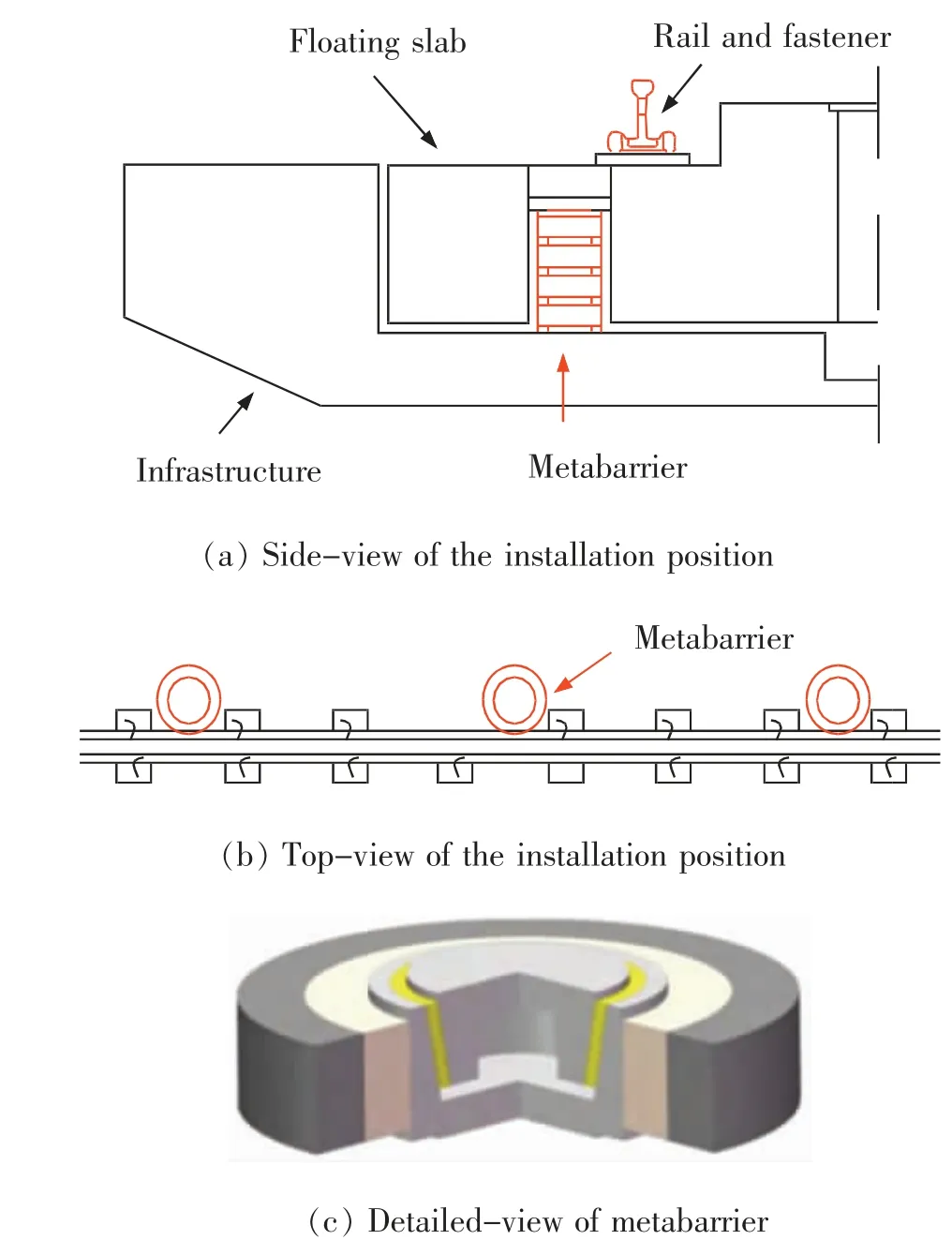
图5 地铁浮置轨道板中的超屏障Fig.5 Metabarrier in the FST

李粮余[47]采用多刚体动力学软件UM与有限元软件ANSYS 联合仿真， 基于声子晶体局域共振禁带机理，对新型声子隔振垫及普通隔振垫轨道结构的隔振效果进行对比分析，新型声子晶体隔振垫能加强63～100 Hz 频率范围内的减振效果，还可将振动能量转化为内能消耗。 徐涆文等[48]分析了弹性短轨枕轨道的声振特性，发现基于周期结构原理建立的轨道模型能够消除边界反射波的影响，且弹性短轨枕轨道的隔振率在整个频率段同普通板式轨道相比具有较为优良的隔振性能。 Hu[49]结合弹性波理论和布洛赫理论，提出了一种新的周期性分层轨道结构， 通过优化几何参数和材料参数控制带隙，以减轻轨道交通造成的振动。 徐司慧等[50-51]为分析黏弹性层状周期板在轨道交通领域的隔振性能，针对板结构的基本形式和单位移动谐荷载，提出了对边自由对边简支板动力计算的近似理论与解答，并对黏弹性层状周期板的减振效果影响因素进行了分析，进而对其减振设计提供一些有益思路。 为进一步利用两种带隙达到更加有效地抑制轨道结构振动噪声，Wang[52]引入局域共振机理，研究了局域谐振器的轨道结构，拓宽轨道结构的带隙范围,如图6所示，轨道结构产生新的局域共振带隙和轨道结构的固有带隙间耦合和转化， 使得带隙宽度最大化，从而实现轨道结构中弹性波控制。

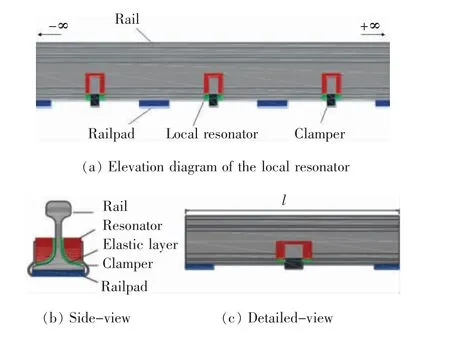
图6 带局部谐振器的无限周期轨道结构Fig.6 Infinite-periodic track with local resonator

3.2 声屏障降噪控制

Koussa等[53]研究表明传统声屏障内侧附加声子晶体结构，可有效控制中高频范围内的交通噪声传播。 Morandi等[54]通过3 层PVC 管周期排列而成的声子晶体声屏障足尺模型试验，研究了其对声波的反射和透射特性，发现最大插入损失位于Bragg带隙频率附近。 Elford等[55]为克服晶格尺寸的限制，利用竹、木、金属等材料作为散射体，为避免整个晶体尺寸的必要的增加，提出一种类似于亥姆霍兹共振机理的声学共振声子晶体系统，通过实验验证了布拉格带隙和局域共振带隙所实现的衰减水平达到25 dB， 为实现较小晶格尺寸的声屏障技术提供了可行性。 张佳龙等[56]提出一种正八边形孔状局域共振型声子晶体结构，通过局域共振单元与弹性波耦合作用，对带隙宽度和弹性波衰减速度进行控制,进而控制隔声特性达到良好的隔声效果。 易强[57]基于声子晶体带隙理论提出一种气固周期型声屏障，如图7所示，采用传递矩阵法研究了其声波带隙特性，研究结果表明气固周期型声屏障中固体材料密度的增加可以显著降低带隙起始频率，同时使截止频率升高、带隙宽度增大，气固周期型声屏障不仅能提高声屏障降噪效果，还可实现声屏障的轻质化。上述研究体现了声子晶体类声屏障能有效改进传统声屏障在主动控制噪声频带范围方面的不足，在散射体材料选择到晶格尺寸改进方面，以及有效利用布拉格带隙和局域共振带隙两种带隙方面都有很大的进展。

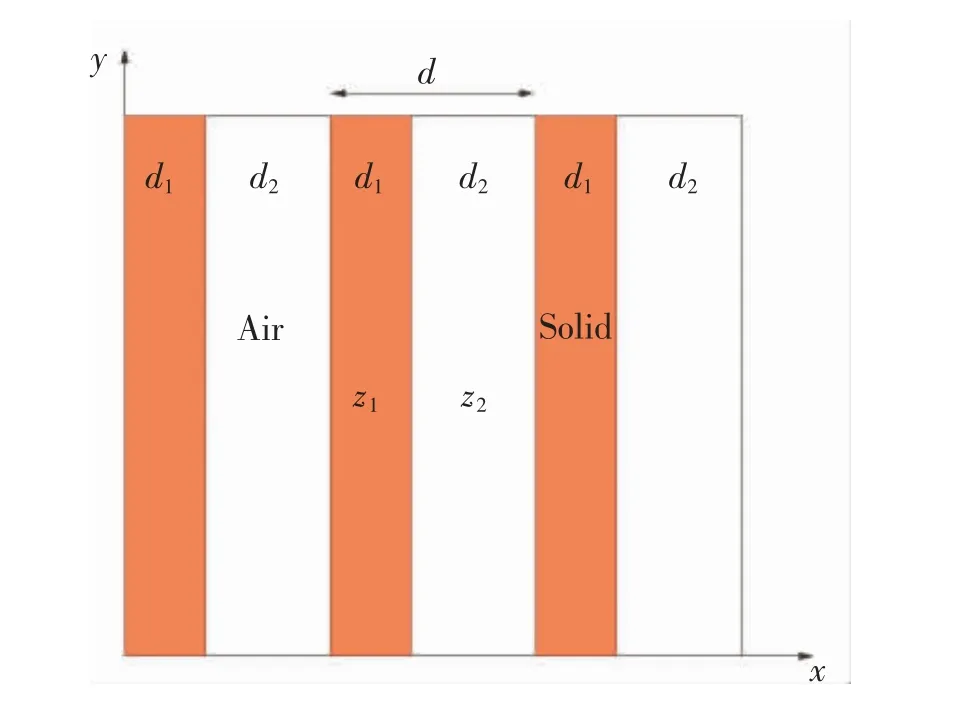
图7 气-固周期型声屏障Fig.7 Air-solid periodic sound barrier

3.3 环境振动减振控制

轨道交通运行等引起的环境振动问题越来越受到研究者关注。 环境振动大多通过土体传播，因此在土体中设置隔振屏障可有效抑制环境振动的传播，石志飞、程志宝等[58-61]长期以来利用声子晶体和周期结构理论，对周期性排桩和连续墙在铁路环境振动控制方面做了许多有价值的研究。 Huang[62]通过数值分析和实验验证提出了一种由周期布置的空心桩组成二维周期桩屏障系统，可产生低频或中频衰减带隙，来降低低频范围的环境振动。 Meng[63]基于偏微分方程(PDE)的有限元方法，研究了设置周期性桩屏障的单相土中平面波的传播和衰减问题，将单相土和桩屏障看作一个周期系统计算了其衰减区域， 验证了时域内周期性桩屏障隔离效果。张冰[64]采用COMSOL有限元软件,建立了周期性排桩固/固物理场耦合仿真模型,对布拉格散射型周期性排桩的影响因素，以及局域共振型周期性排桩的影响因素进行了单因素影响规律分析，并通过正交试验及影响因素分析，提出了布拉格散射型和局域共振型周期性排桩设计的优化参数组合方案。 Meng[65]结合比奥特理论与声子晶体理论，使用流体饱和孔隙弹性介质模型对频域内周期性桩屏障的减振特性，及周期性桩屏障的色散性质进行了研究，发现周期性桩屏障的实际频带可分为高速纵波带、低速纵波带和剪切波带3个类别。 并深入讨论了土壤骨架、土壤渗透率、流体粘度以及复杂分散体和饱和度的几何参数对衰减域的影响。 孟庆娟[66]基于周期理论和Biot波动理论，应用COMSOL PDE 有限元法分析了饱和土中周期性排桩的排数和桩长等参数对衰减域的影响。Liu等[67]基于遗传算法和有限元方法, 对周期屏障进行单目标优化和多目标优化进行拓扑优化，研究了根据环境振动减振需求实现表面波带隙(SWBGs)的带宽合理配置的机理。姜博龙[68]利用基于声子晶体理论的平面波展开法求解周期波屏障（排桩－土系统）的衰减域，并将该周期性波屏障应用于某工程预测模型中，验证其衰减域并预测其隔振效果。 Zhao等[69]通过有限元分析研究了一种利用声学黑洞(ABH)结构的低频和多模态特点，产生ABH橡胶和钢谐振器之间的耦合振动的新型声子晶体隔振器的结构(NPCVI)，对其带隙形成机理进行了研究， 并建立了浮置板轨道-隧道耦合动力学分析模型， 分析了在各种轨道不平顺激励下的NPCVI对隧道环境振动的隔振性能，研究结果表明，在不同的列车速度下，NPCVI表现出了比钢弹簧隔振器更加优越的隔振性能。 根据以上研究，基于声子晶体理论的周期性排桩等减隔振屏障的研究在带隙形成机制、理论分析方法、以及结合多参数的带隙拓扑优化等多个方面有了较深入的研究，并有初步工程应用研究。

4 结束语

声子晶体结构中弹性波传播特性的研究已经有了一定的基础，并在理论和实验上均已验证了带隙在减振降噪方面有着潜在的应用前景。 基于声子晶体理论调节轨道交通中周期性结构及周期性减隔振构造物的几何/材料参数，为通过人为调控带隙（衰减域）的位置、宽度实现对弹性波传播的针对性抑制来达到铁路减振降噪的目的提供了现实的可能。

本文介绍了声子晶体理论带隙的形成机制，并对轨道交通中基于该理论的周期性轨道、周期性桥梁和周期性隧道的振动分析理论，以及在周期性轨道减振、声子晶体类声屏障降噪控制和周期性隔振屏障等减振控制方面的研究进展进行了回顾，就目前的文献调研结果来看，后续的发展主要有以下几点：

1） 目前基于声子晶体理论的轨道交通减振降噪方面的理论研究越来越被学者们重视，在周期结构的波传播理论取得了可喜的进展，但距离减振降噪工程实际应用还存在一定的局限，特别是在周期性轨道结构和周期性桥梁结构减振控制方面尚待进一步系统和深入，目前尚未有通过人为调整带隙实现周期性桥梁减振方面的文献研究。

2） 目前基于声子晶体的铁路中周期性结构的理论研究主要为超长直线状结构，而实际工程的位于曲线段的周期性轨道、桥梁、隧道结构还未对曲线段和对应的支承条件对其带隙形成机制的影响进行深入研究。

3） 目前的理论研究鲜有结合现场实际线路的减振降噪效果的试验测试展开，后续研究可结合实际工程通过满足实际线路减振降噪需求的带隙调控措施，灵活地调控和抑制弹性波，达到预期的减振降噪效果。 此外后续研究还可根据实测的铁路中周期性结构的振动局部化现象来探测铁路中周期结构因病害和故障产生的失谐。

4） 声子晶体理论为铁路减振降噪突破了传统材料和传统结构的束缚，为调控弹性波的传播特性带来了全新的自由度。 为铁路的减振降噪控制理论发展带来了新的思路， 应进一步结合拓扑优化、缺陷态、弹性波群速度等特性与带隙形成机制之间的关系，进一步为设计满足减振需求的措施和产品进行更加深入的研究。

5） 基于声子晶体理论的铁路减隔振动研究中，在带隙位置和带隙带宽的调控方面受到了晶格尺寸的限制，例如周期性轨道板和周期性桥梁的晶格是不能轻易改变的，为了解决这个不利因素，可尝试从集成多个不同的共振单元或引入额外的物理场(如引进压电元件、惯容器等) 来设计主动式的声子晶体结构， 从而根据需求灵活地调控弹性波，同时增材制造技术 (如3D 打印) 的技术进步带来的其材料、加工尺寸及精度可以促进声子晶体类声屏障技术的发展。