SSA优化融合CNN的电机轴承故障诊断方法研究
2021-09-14姜宇宏
孙 波,姜宇宏,杨 青
(沈阳理工大学 自动化与电气工程学院,沈阳 110159)
电机轴承作为工业生产中的关键部件,被广泛应用于风力涡轮机、高速列车、飞机发动机等大型复杂设备中。由于恶劣的工作环境和高强度的运行模式,电机轴承很有可能发生意外故障,导致增加停机时间和经济损失[1]。因此,对电机轴承进行故障诊断,从而降低其发生故障的风险概率,提高其安全性[2]。
深度学习是一种自动特征学习方法,由于其深层架构,使得绝大部分领域中都有其应用,如即时视觉翻译、自动驾驶汽车、语音识别等[3-5]。近五年来,深度学习方法在电机轴承故障诊断方面也取得了诸多研究成果[6-7]。在研究中,卷积神经网络(Convolutional Neural Network,CNN)[8]、深度自动编码器(Deep Auto-encoder,DAE)[9]和深度信念网络(Deep Belief Network,DBN)[10]这三种模型被广泛应用。
文献[11]利用PSO+CNN的故障诊断方法,实现了轴承故障诊断较高的准确率和稳定性。文献[12]利用改进ReLU+残差神经元的RLCNN网络模型,实现了对轴承的故障诊断,并达到了较高的故障诊断准确率。文献[13]利用一维多尺度卷积神经网络故障诊断模型,解决了轴承故障特征的自动提取问题,从而判断出故障发生位置和其损失的严重性。文献[14]提出了一种基于一维时间序列编码到二维图像的CNN框架,有效地进行了轴承故障特征的采集与识别,并达到了较高的故障诊断准确率。文献[15]分析了在工程领域内具有应用前景的、包含麻雀搜索算法(Sparrow Search Algorithm,SSA)等多种群智能优化算法的优缺点,得出SSA在收敛性、寻优能力和稳定性等方面具有很大优势。
利用CNN进行特征提取时,突出之处在于其能够自主地提取复杂的非线性关系,因此,CNN在视频分析、环境感知等方面取得了良好的效果。但CNN在进行分类时,网络结构与层数的选择、内部各参数的设置等因素都会对最终的结果造成很大影响,所以利用SSA算法的性能特点[16]对CNN的网络模型进行优化具有一定的可行性。
综上,本文以电机轴承的振动信号作为分析对象,利用一维卷积和二维卷积对数据进行预处理操作,同时训练融合的CNN模型;利用SSA对各网络权重及参数进行优化处理,包括初始学习率、迭代次数、batch_size等主要参数,从而进一步提高融合CNN的故障分类精度。
1 卷积神经网络的基本原理
1.1 一维卷积神经网络
一维卷积神经网络经常被用在时间序列模型中,如图1所示。
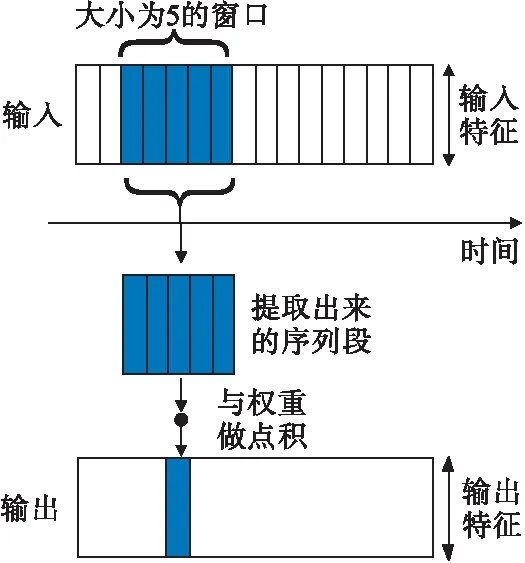
图1 经典一维卷积神经网络工作原理图
经典一维卷积工作原理是从输入特征中提取相对应的时间序列片段,再进行点积运算,最后输出特征。因此,使用不同大小的卷积核进行操作,即可对不同维度上的特征信息进行融合,从而达到对数据升维和降维的需求[17]。所以,在进行轴承数据处理时,一维卷积神经网络可以提取时序特征,这也正是浅层机器学习模型所不具备的优势。
1.2 二维卷积神经网络
经典的二维卷积结构至少包含一层卷积层,并由多个卷积核对图像进行局部处理,从而完成特征提取,再进行最后的合成处理。卷积、池化和全连接层是CNN的主要模块,如图2所示。
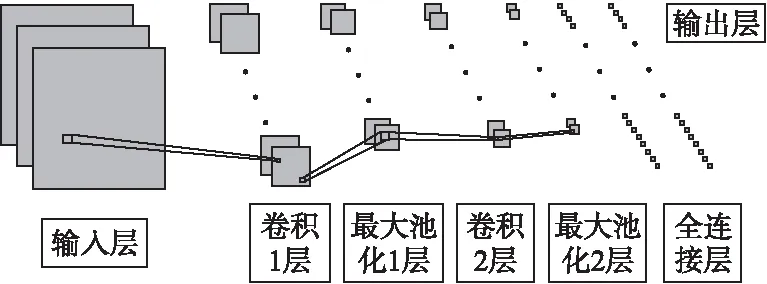
图2 经典二维卷积结构图
经典二维卷积神经网络的工作原理如下。
首先,由多个神经元组成的首层卷积层执行运算,同时运用反向传播算法获取卷积核参数;其次,第一层池化层执行池化运算,将卷积后得到的特征图谱进行池化操作,缩小其尺寸;然后,进行第二层的卷积池化层运算,以便取得更明显的参数特征,同时也可获得更高级别的抽象特征;最后,全连接层执行运算操作,得到模型训练的最后结果。即卷积层执行特征提取,池化层执行特征降维,从而防止过拟合。
1.3 融合卷积神经网络
本文使用的方法是将一维卷积神经网络与二维神经网络进行融合,同时对电机轴承数据集进行训练,即分别执行多个卷积层、池化层运算;然后在汇聚层将两组神经网络池化层的输出连接成一个向量,输入到全连接层;最后由全连接层输出提取到轴承故障信号[18]。诊断流程如图3所示。

图3 融合CNN诊断流程图
2 SSA优化融合CNN故障诊断模型
2.1 SSA基本原理
麻雀群觅食过程中,根据适应度值的评估,找到食物较好的个体作为发现者,而剩余其他个体作为跟随者。发现者负责寻找食物的同时,也会向整个种群中其他个体提供食物的大概位置;同时,整个种群中会有一小部分个体执行监视操作,也有一小部分个体会与其他同伴抢夺资源,以达到提高自身捕食准确率的目的。种群中选取一定比例的个体进行侦查预警,如发现危险则放弃食物。即是一种发现者-跟随者模型,同时叠加了侦查预警机制[19]。
2.2 SSA优化融合CNN流程
SSA优化融合CNN流程步骤如下。
步骤一:初始化麻雀种群数,设置最大迭代次数、最大最小寻优边界范围等相关参数、初始化种群中发现者和跟随者的比列。
步骤二:计算适应度值,同时排序,找出当前最好和最差的个体。
步骤三:对发现者的位置XF,W利用公式(1)进行更新。如果预警值较小,说明没有捕食者出现,周围环境安全,发现者可以执行广泛的搜索;如果预警值较大,说明有捕食者出现威胁到了种群的安全,种群中的某些个体会发出警报,此时所有个体需要飞去其他安全的地方进行觅食。
(1)
式中:Xm,n表示种群中第m个个体的第n维位置;t为当前迭代数;n=1,2,3,…,d;α∈(0,1]为随机数;K为常数;Q为随机数且服从标准正态分布;L为1×d的矩阵;R2∈[0,1]为预警值;SK∈[0.5,1]为安全值。
步骤四:对跟随者的位置XGW利用式(2)进行更新。此时,一些能量值较低、适应度值较差的跟随者,有可能飞到其他地方进行觅食;还有一些会围绕在最优的发现者周围进行觅食,其间也有可能发生食物的争夺,使自己变成发现者。
(2)
式中:XW为当前麻雀种群中最差位置;XP为当前发现者中最佳位置;A为1×d的矩阵且满足A+=AT(AAT)-1;i为麻雀数量。
步骤五:选取麻雀种群中的某些个体作为警戒者,随机产生其位置,模拟危险并进行位置移动,利用式(3)进行警戒者位置XJW更新。
(3)
式中:Xb为当前麻雀种群中最佳位置;β为随机数且服从标准正态分布;ε是常数;fi为当前麻雀的适应度;fg为当前全局最优适应度;fw为当前全局最差适应度。
步骤六:如果搜索到最优解,则退出SSA算法,输出最终结果;反之,则循环运行二~五4个步骤,流程如图4所示。
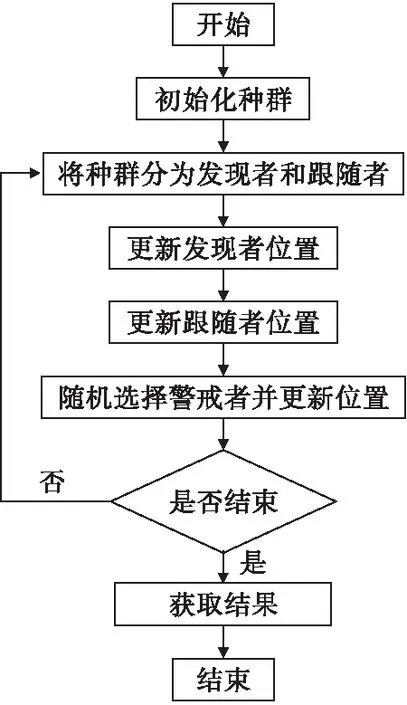
图4 算法流程图
3 实验验证
为验证所提出的方法在电机轴承故障诊断时的可行性,本文采用西储大学的电机轴承数据集,通过Python软件对数据进行实验及测试。轴承故障数据描述及样本分布如表1所示。

表1 轴承样本分布
实验样本选用48kHz的轴承故障数据,分别选取7mil、14mil和21mil故障体量级别下,三种包含轴承内圈、外圈及滚动体的故障位置,外加一组正常数据共10组,按7∶2∶1的比例划分训练集、验证集及测试集(其中训练集和测试集无任何交集)。分别对训练集、验证集和测试集进行处理。SSA优化融合CNN的故障诊断结果如图5所示。
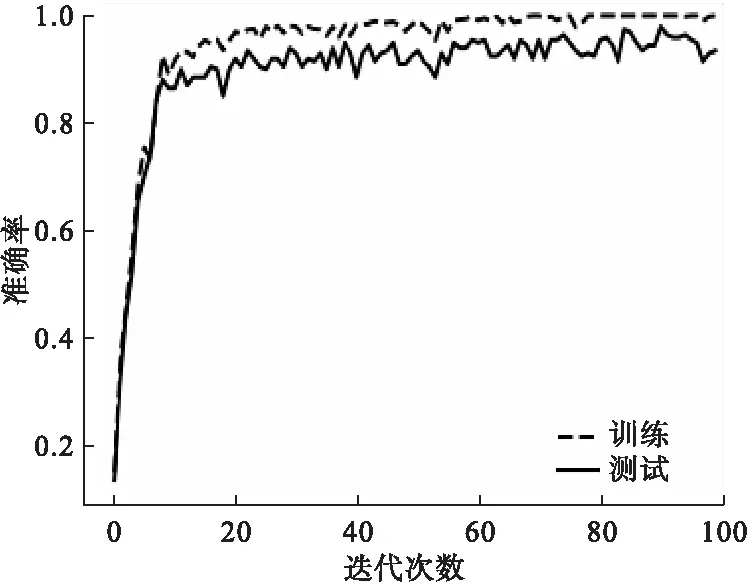
图5 SSA优化融合CNN故障诊断结果
训练SSA优化融合CNN的模型,得到超参数,重新训练模型并对测试集分类,其测试集结果诊断率为98%。SSA优化融合CNN的损失曲线如图6所示。
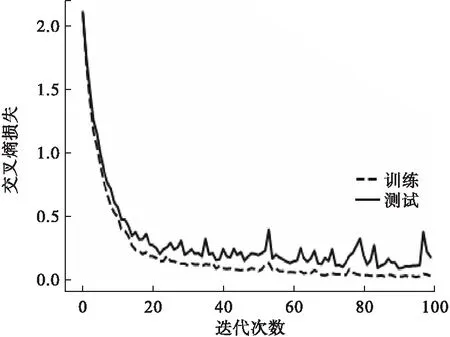
图6 损失率曲线
用训练集进行融合CNN训练,优化时SSA以验证集的错误率为适应度函数进行优化,使得训练出来的融合CNN在验证集上有最低的错误率。表2为不同诊断方法对比结果。

表2 诊断对比表
对比表2中的诊断结果可以看出,利用SSA优化融合CNN网络(本文方法)可以达到较高的准确率。
4 结束语
基于麻雀搜索算法和融合CNN网络,提出了一种SSA优化融合CNN的电机轴承故障诊断新方法。结合融合CNN网络在轴承故障诊断方面的优势及SSA算法的性能特点。对比实验结果表明,本文所采用的麻雀搜索算法优化融合CNN网络的电机轴承故障诊断方法有效,能够提高轴承故障诊断精度。
