一种面向无线传感器网络的多数据融合模型设计

石征锦，王博伦，谢 峰，刘子弘

(沈阳理工大学 自动化与电气工程学院，沈阳 110159)

针对传统温室系统高度依赖人工操作、对作物生长周期及能量供需控制能力较差等缺陷，提出利用无线传感器对多种、多路数据采集并智能控制的新一代智能高效温室解决方案[1]。作物生长环境复杂多变，传感器阵列采集获取多路异构数据集，中心控制器能否及时接收精准的采集数据并及时将相应反应动作信号传达至执行机构十分重要[2]。由于传感器测量误差及无线传输能力的限制，系统整体控制实时性及效果呈现明显不足，直接影响作物在全生命周期的健康指数，降低其成活率及优育率。

对于温室无线传感器网络中复杂多数据采集传输问题，采用数据融合方法进行分布式处理，降低系统对无线传输及中心控制器数据处理能力需求，该问题归类于多数据融合技术[3-4]。针对不同应用背景，多数据融合技术路线众多[5]。李昕等[6]在面向工业环境温湿度数据采集中提出一种基于模糊逻辑的多传感器融合方法，通过实验证明了该方法具有较强的实用性能；万树平[7]在多传感器数据特征值融合中提出利用统计理论中的最小绝对偏差估计方法，在自适应权值的基础上，通过求解条件极值问题得到融合权值并得出融合结果，该方法稳定性较好；刘尖学[8]在面向设备能量受限、数据冗余量较大的可穿戴无线传感网络中提出一种基于模糊神经网络的数据融合算法，实验表明该方法可在保证较高网络预测准确度的同时有效降低网络节点能耗。

针对温室无线传感器网络中异类共存、采集数据量较大且硬件以高性价比设备为主的现状，提出卡尔曼滤波器(Kalman Filter)与径向基函数(Radial Basis Function，RBF)神经网络下支持向量机(Support Vector Machine，SVM)相结合的多数据融合处理模型。利用信息融合思想，通过信息采集、预处理、分类融合等步骤完成对多维、异类传感器采集的离散数据集在感知层进行数据信息分类与优选[9]。该方法可在复杂工况环境下，对无线传感器物理数据采集系统进行优化，并降低对硬件设备处理性能的负荷需求，提高系统整体通讯效率。

1 多传感器数据融合原理

多传感器数据融合为多维度数据处理过程，对多路同类或异类传感器数据集进行自动检测、关联、相关及组合等方式处理，可有效克服单传感器的局限性并对目标物以稳定、可靠的现实状态估值反映[10]。由于各传感器的不确定性，数据融合过程实则为对传感器矩阵采集数据集的推理分类、选择与决策输出过程。

智能温室中需要多点采集温度、湿度、光照强度及二氧化碳浓度等物理数值，并通过无线通讯ZigBee技术树状网络对数据处理并传输至中央控制系统。无线传感器树状拓扑图如图1所示。

图1 无线传感器树状拓扑图

多传感器协同采集信息时存在交叉冗余性数据，同时传感器精度较差时输出多维度离散数据集，均可导致系统的处理能力及稳定性降低[11]，故需要系统在采集、传输各阶段对数据进行分析和处理[12]。

分布式无线传感器采集获取数据子集Xab(t)={Rab1(t)，Rab2(t)，Rab3(t)，Rab4(t)}，在基于ZigBee技术的无线传感器中利用Kalman滤波器对数据子集Xab(t)进行预处理，提高传感器采集精度，并通过基于RBF神经网络的支持向量机训练学习，对数据进行分类。数据融合过程为并联型结构[13]，可对所有数据子集同时进行优化并提取特征和分类处理，确保数据处理过程的效率及公平性。多传感器数据融合模型结构原理如图2所示。

图2 数据融合模型原理

2 单一传感器数据融合预处理

利用卡尔曼滤波器进行系统状态估计可对单一传感器采集数据样本集进行除噪声线性优化，并可对多数据集进行整体筛选，去除异常数据，使各采集数据集回归近似线性[14]。

卡尔曼滤波器利用反馈控制原理对状态进行估计，包含一个状态转移模型作状态更新及一个测量模型反馈作测量更新，其原理如图3所示。

图3 卡尔曼滤波器原理图

状态转移模型根据k-1时刻数据估算k时刻的状态变量X及先验误差协方差P(k∣k-1)，估算公式见式(1)和式(2)。

X(k∣k-1)=AX(k-1∣k-1)+BU(k)

(1)

式中：X为状态变量；A、B为系统参数矩阵；U为目标对象控制变量。

P(k∣k-1)=AP(k-1∣k-1)AT+Q

(2)

式中：P为状态变量X的协方差；Q为系统过程协方差。

测量模型利用状态观测数据及前一刻估计值修正预测状态，得到最佳状态估值X(k∣k)、卡尔曼增益Kg(k)及修正后的预测误差协方差P(k∣k)，分别见式(3)、式(4)及式(5)。

X(k∣k)=X(k∣k-1)+Kg(k)(Z(k)-HX(k∣k-1))

(3)

(4)

P(k∣k)=(1-Kg(k)H)P(k∣k-1)

(5)

式中：Z为状态观测数据；H为测量参数矩阵；R为测量噪声[16]。

根据离散卡尔曼滤波原理可实现对单一传感器采集的一维数据预处理。考虑系统运行环境较为复杂且传感器以分布式列阵，传感器采样时可能在某时刻存在较大误差，该点称之为野点。为得到更加精准的数据子集，需要对野点进行识别与剔除。

若输出数值集存在异常点，利用式(6)判别该点采集数据是否需要剔除。

(6)

式中E为传感器门限参数。

若式(6)为真，则该野点偏差较大，不具备统计学意义，需被剔除。

3 多传感器数据特征推理

3.1 多传感器数据子集相关性分析

多传感器数据融合前需对各类传感器数据集进行分析，确定最佳分类融合方案。针对温室的控制需求与控制目的，根据相互独立且合理的原则，将加热、加湿、通风、补光、遮光和CO2浓度共六种控制办法分为27组控制决策，如表1所示。

根据表1的控制决策，对目标数据子集利用协方差方法，开展各传感器数据(物理量)的相关性分析。物理环境采集样本数据散点矩阵分析如图4所示。

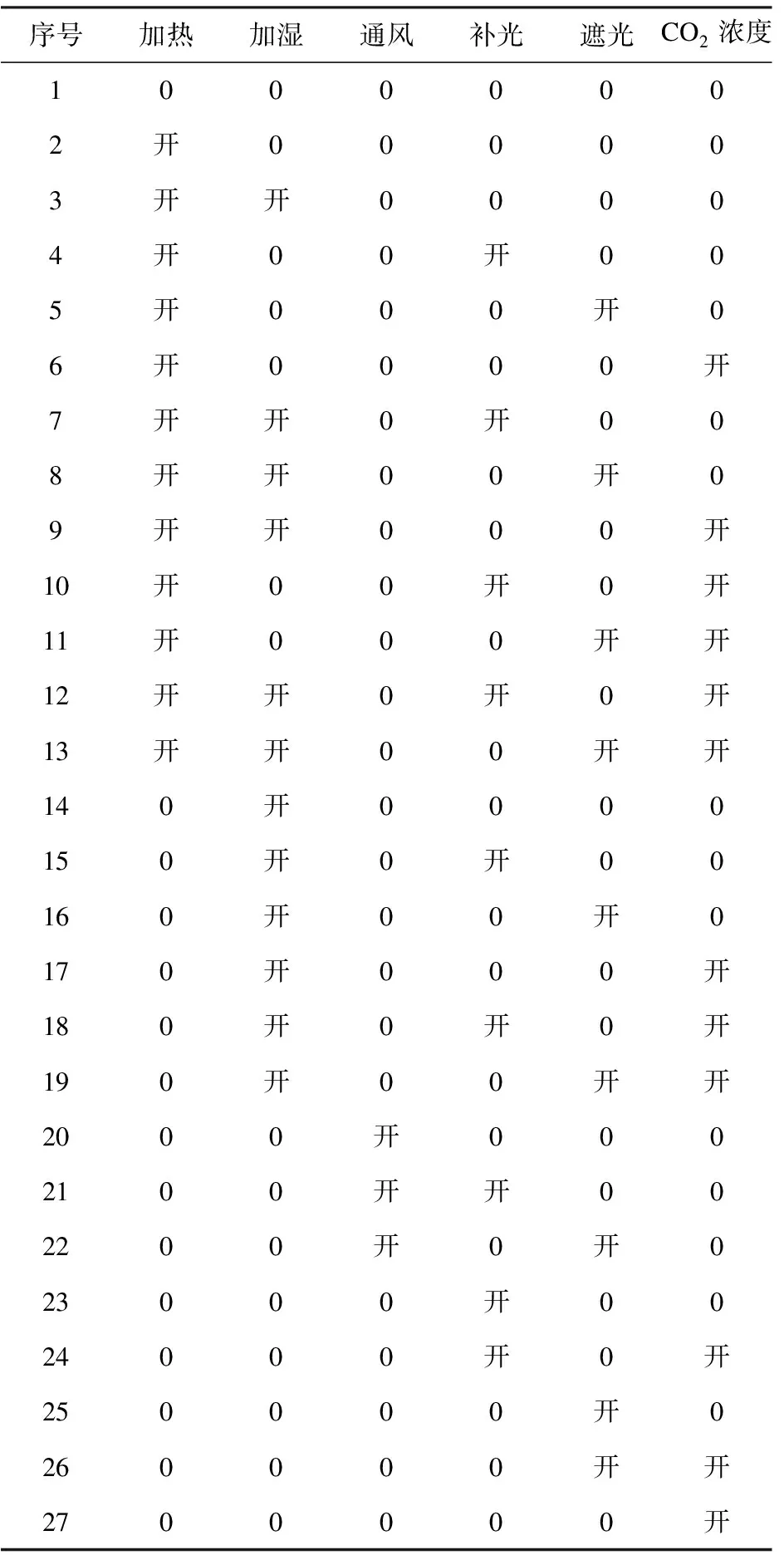
表1 模型对应控制决策

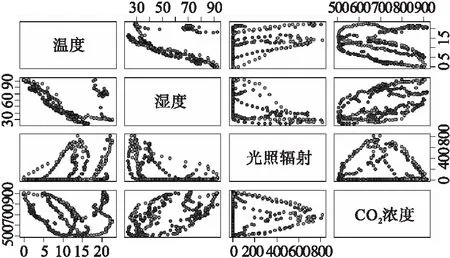
图4 物理环境采集样本数据散点矩阵分析

为得到更加精准的量化环境物理量方法，引入相关性系数，其计算方法见式(7)，四种环境物理量相关性系数计算结果见表2所示。

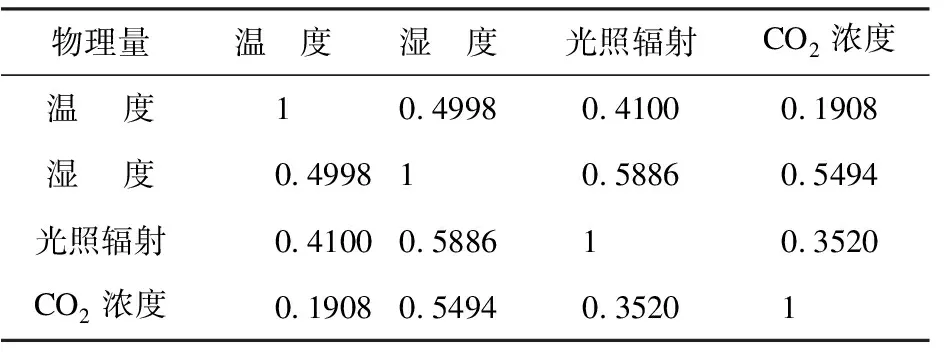
表2 四种环境物理量相关性系数

(7)

式中：r为相关性系数；σ、β为对比的两组数据。

由表2可见，部分数据子集之间线性相关性较低，故在模型中对多数据融合方法选用非线性回归进行处理。针对样本数据子集特性，选择加入高斯核函数的支持向量机方法对数据集进行分类。

3.2 支持向量机核方法数据分类

智能温室中央控制系统在接收多传感器数据子集前，对各子集元素打乱后重新分类，利用支持向量机算法通过训练学习样本对数据分类，得到具有一定特征的最优超平面。

SVM的基本思路是在所有数据组成的集合w={(x1，y1)，(x2，y2)，…，(xn，yn)}空间中寻找最优超平面。最优超平面目标函数为

(8)

使用拉格朗日函数对式(8)进行对偶变化，得到最大化函数，见式(9)。

(9)

式中αi为拉格朗日乘法子。

对于多传感器数据融合非线性问题，支持向量机加入核方法——径向基函数，可使数据融合模型在多维度下对输入数据进行聚类，寻找最佳超平面。

在SVM中加入径向基函数，见式(10)。

(10)

式中：K为空间内任一点到中心点的欧氏距离；xc为空间中心点；γ为基函数参数，调整γ可改善SVM的分类精度。

加入RBF核函数后SVM的输出值y的计算式为

(11)

根据表1中模型决策分类任务需求，经过预处理的传感器数据集组成SVM测试集与训练集。采用网格搜索法在设定范围内对训练集进行训练，获得重要参数c(惩罚系数)与gamma(核参数)。

将获得的(c，gamma)参数组带入面向测试集数组的SVM算法中计算识别准确率Fc，并将结果进行记录、比较寻优，得出最佳分类结果与支持向量机模型。基于SVM算法的温室数据融合分类流程如图5所示。

图5 基于SVM算法的温室数据融合分类流程

4 实验与测试

为验证模型融合处理能力，使用数据样本对模型进行分类训练。实验包括预处理能力测试与模型分类能力测试两部分。

为降低硬件成本，物理数据采集所用传感器均为较常见且性价比较高的型号，其中温度测量选用DS18B20型，湿度测量选用HS1101型，光照度测量选用BH1750型，CO2浓度选用NDIR红外吸收原理传感器。采用Matlab对采集数据进行预处理，预处理后数值与原始数据进行对比如图6所示。

由图6可见，经过模型处理后的数据与原始采集数据相比，误差有明显改善且对野点的甄别较为敏感。预处理可将连续采集数据线性化，减少由于传感器误差导致的模型分类错误与执行机构的误操作，采集数值在阈值附近时尤为有效。

图6 传感器原始采集数据与预处理后数据

预处理后可得到一组准确率较高的异构温室环境物理数据，对其进行模型分类训练与测试。将数据导入Matlab，建立训练集、训练集标签、测试集及测试集标签共四组数据变量，其中训练集标签与测试集标签根据表1制定的系统控制决策选取设定。采用LIBSVM工具箱[15]在Matlab软件环境下开展训练测试。

基于网格搜索[16]法面向训练集寻参，即在[2cmin，2cmax]范围内确定惩罚系数c、在[2gmin，2gmax]范围内确定核参数gamma，设定cmin=-20、cmax=20、gmin=-20、gmax=20，并设定c步进值cstep=1与gamma步进值gstep=1。

将获得的(c，gamma)参数组带入测试集，根据筛选原则(准确率Fc>75%)确定有效(c，gamma)组合。有效SVM候选参数如表3所示。

表3 有效SVM候选参数

由表3可见，最优(c，gamma)对为c=210=1024、gamma=2-5=0.03125，其准确率为Fc=95.2624%，获得分类模型。实际测试交叉验证准确率结果表明，该模型具有较强的分类能力和泛化能力。将训练获取的分类模型导入原有设备中，无需改变硬件设备即可高效完成数据分类任务，实现分布式数据处理，减少无线传输数据量，实现高效控制。

5 结论

建立了多数据融合模型，该模型结合了卡尔曼滤波器的数据预处理与基于支持向量机的非线性分类，采用该模型对实际应用工况数据进行分析。模型对数据组的训练结果表明：模型在预处理与数据分类方面具有较高可靠性；针对智能种植系统的控制需求与成本限制，通过该模型修正，高性价比传感器设备可获得较高感知精度；模型在感知层即可完成数据精简处理，可有效降低对无线通信网络硬件的带宽需求。其可泛化应用于各类多数据采集控制系统，依据模型分布采集、分布处理、分布决策的特性可针对灵活组网的低成本复杂无线传感器网络进行有效优化。