四足机器人不规则地形稳定方法研究

刘 军，王 楠

(沈阳理工大学 自动化与电气工程学院，沈阳110159)

一个性能优良的四足机器人在规则与不规则地形中移动时，应能适应环境变化，在受到干扰时能够保持或恢复自身的平衡状态[1]。在类人机器人领域，通常有三种策略来恢复机器人稳定，三种策略分别在机器人受到不同程度的扰动时应用，此时扰动分为较小、适中、较大三种状态；在扰动较小时采用踝关节或髋关节策略来调节主体位置方向维持平衡[2-4]；当扰动加强时采用步进策略[5-6]；扰动较大时，为避免机器人在降速时发生难以预料的损伤，采用降速控制法[7-8]。

在以往的四足机器人稳定方法研究中主要有两种方法。第一种方法，为解决四足机器人的大量自由度在实际计算中过于复杂的问题，提出了几种简化模型，如线性倒立摆模型(Liner Inverted Pendulum Model，LIPM)[9-10]，并在此基础上提出了零力距点补偿方法(Zero-Moment Point，ZMP)和模型预测控制算法(Model Predictive Control，MPC)[11-13]及将四足机器人视为二足模型提出了二连杆倒立摆模型[14]；其中ZMP在早期常用于判定双足机器人在行走过程中的动态稳定性[15]。在第二种方法中提出了建立机器人的全身动力学模型来解决稳定问题。还有一些研究则提出了基于接触力调节的平衡恢复算法，如文献[16]设计的力-姿态反馈控制器(Force-Posture FeedbackCompensation，FPFC)，FPFC采用机器人足端的力传感器和陀螺仪采集到的反馈信号来对机器人姿态进行调整。文献[17-18]提出了基于动量的平衡控制器，通过约束优化问题的定义，计算所允许的关节加速度，以获得所需的角动量和线性动量。也有通过深度学习对四足机器人进行大量训练与学习，从而实现无建模控制[19]。C Gehring等研究了在平坦地形下基于接触力的四足机器人平衡控制算法[20]。

本文设计一个基于四足机器人全身动力学的平衡控制器，以每条腿的足端位置向量为入手点，通过实时获得每条腿的反馈信号，调节主体加速度来维持机器人平衡，抵消机器人足端与障碍物产生的干扰；设计的平衡控制器具有一定的鲁棒性，能实时调整补偿值，提高四足机器人行走时的稳定性，同时采用贝塞尔曲线对足部轨迹进行规划。

1 运动学与动力学模型

本文使用的四足机器人由一个主体框架和四条腿组成，图1为四足机器人模型，图2为四足机器人简化模型。本文设计的机器人每条腿都有三个自由度。

图1 四足机器人模型

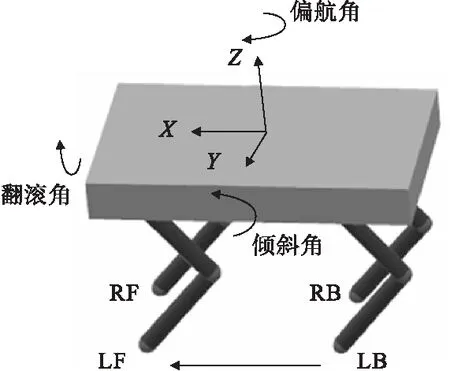
图2 四足机器人简化模型

图2中RF、LF、RB和LB分别表示机器人右前腿、左前腿、右后腿和左后腿。

本文采用显式动力学来推导机器人动力学模型[21]。如图2所示，其系统运动相对于地面惯性参考系(XYZ)进行分析，取系统势能为零。该系统的一般拉格朗日公式为

(1)

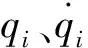
(2)

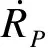
(3)

(4)

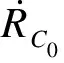
(5)

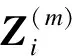
(6)

简化得到

(7)

(8)

(9)

(10)

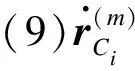
(11)

注意：T的表达式(7)用身体位置与方向固定的向量表示，必须对每一项使用适当的变换矩阵来做式(1)中所需的微分。

广义坐标向量q表示为

(12)

(13)

(14)

(15)

式中：δ0∈R6×1为主体位置和方向的矢量矩阵；θ∈Rn为关节位置向量；n为各腿关节个数。系统引入了代数约束，利用文献[23]提出的自然正交补法可得到独立运动方程组。该机器人运动学方程可表示为

(16)

设

(17)

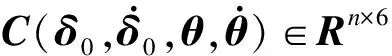
2 步态和足部轨迹规划

2.1 步态轨迹规划

四足机器人的步态可分为静态和动态两种。

静态步态：包含行走步态和爬行步态；机器人使用该步态时，在行走周期的任意时刻都保证有三条腿与地面接触，其质心的垂直投影始终保持在机器人支撑腿形成的多边形内。动态步态包括对角小跑、跳跃、踱步和奔跑；动态步态运动速度较快，且运动周期中任意时刻最多两条腿与地面接触，机器人质心垂直投影没有停留在机器人支撑腿形成的多边形内，但也能保持动态平衡。

当机器人处在平坦或不规则地形时，其稳定性都非常重要。为验证本文所设计的平衡控制器的稳定性与鲁棒性，采用静态步态中的行走步态在仿真环境中进行测试。

行走步态：在一个周期内任意时刻仅有一条腿抬起，并以0.25的相位进行轮流迈步；其序列图如图3所示。

图3 行走步态序列图

2.2 足部轨迹规划

为保证机器人能稳定行走，其足部轨迹应与动物行走轨迹类似，且足端落地时足部轨迹不能对机器人产生较大影响。本文采用贝塞尔曲线对足部运动轨迹进行规划[24]。贝塞尔曲线方程为

(18)

式中：E为控制点；e为控制点个数；i为第i个控制点；t为曲线参数。

四足机器人轨迹规划有多种，如3阶轨迹规划和正弦轨迹规划，但由于这些轨迹规划没有考虑加速度，因此本文采用5阶贝塞尔曲线方程，为

X(t)=E0(1-t)5+5E1(1-t)4t+10E2(1-t)3t2+10E3(1-t)2t3+5E4(1-t)t4+E5t5

(19)

由于机器人初始状态为静止，根据文献[16]定义贝塞尔曲线初始状态为

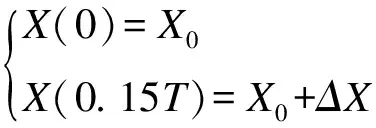
(20)

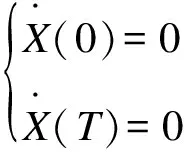
(21)

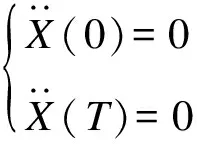
(22)

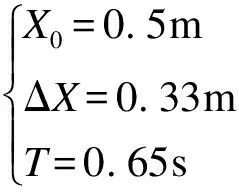
(23)

在式(20)中，X0为机器人脚在X方向上的起始位置；ΔX为脚在X方向上的步距。

将式(20)～(23)初始条件代入式(19)中，得到

X(t)=0.5+3560.41t3-54775.55t4+224720.2t5(0≤t≤0.0975)

(24)

同样，可得到Z轴方向的曲线方程为

(25)

初始状态为

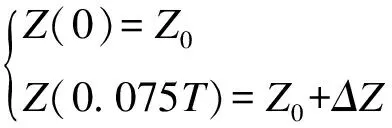
(26)

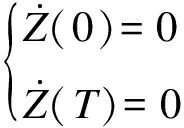
(27)

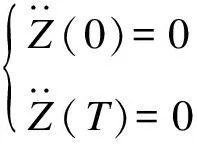
(28)

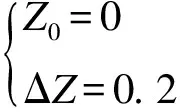
(29)

将初始条件式(26)～(29)代入式(25)中，得到

(30)

在有些塞尔曲线步态方案上，允许用户任意组合前进、侧向与偏转指令，且随时间推移给出足端坐标。贝塞尔曲线控制足端运动示意图如图4所示。

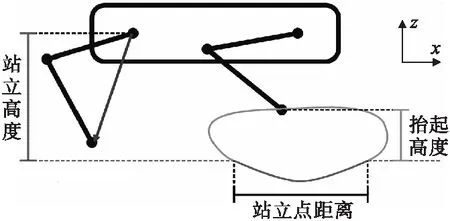
图4 足端运动示意图

图4中抬起高度表示机器人足端距离地面最远距离；站立点距离为机器人足端运动一个周期在地面上相距最远距离；站立高度为机器人中心距离地面最远距离。

3 四足机器人平衡控制器

本文以机器人全身动力学模型为切入点设计平衡控制器。在以往研究中，通过逆运动学模型推导机器人身体位置，必须获得机器人的关节力矩和足端接触力。传统的力传感器噪声较大，导致测量的接触力误差较大，于是通过运动学约束从动力学方程中消除接触力[25-26]。

当机器人站立在环境中时，假设机器人保持静止，初速度为0，运动时与地面存在摩擦力，可得到约束条件为

(31)

式中v为机器人在环境中保持站立腿的数量。此时，定义一个命名为β的独立空间。

(32)

式中θSL为自由腿的关节角。整体结构与独立空间β的关系可以表示为

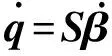
(33)

式中S为映射矩阵。

(34)

其中

(35)

(36)

式中JL，i和Jb，i分别为第i条站立腿和主体雅克比矩阵。

(37)

式中XL，i表示第i条站立腿的足端位置。将式(33)改写为驱动与欠驱动两部分组合，为

(38)

式中：下标un表示欠驱动；u表示驱动。将式(38)进行时间微分，有

(39)

将动力学方程式(16)分解为驱动与欠驱动部分组合，则

(40)

(41)

式(40)、式(41)可写成两个独立方程，为

(42)

(43)

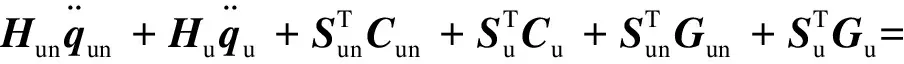
(44)

式中：

(45)

(46)

从Sun和Su的定义可以得到

SunJun+SuJu=0

(47)

本文以四足机器人静止在地面上为例证明式(47)，同样在其他状态下也可通过类似的步骤证明式(47)。

当机器人静止在地面上时，四条腿都与地面接触，可得到矩阵J为

(48)

得到Jun与Ju为

(49)

同样可得Sun、Su为

(50)

将式(49)、(50)代入式(47)中得到

(51)

得到抵消接触力后的运动学方程为

(52)

式(52)应以独立空间表示，将式(39)代入式(52)得

(53)

此时的动力学方程已消去与接触力有关的项，当外部干扰施加在机器人身上时，会使机器人在力作用的方向上有运动的趋势并产生一个初始加速度，导致机器人偏离预期姿态，失去平衡。为抵消干扰所产生的加速度，应对机器人施加一个与之相反的加速度。期望加速度通过式(53)获得，机器人运动时需要较大的位置误差和误差率进行动态调节，所以本文采用比例微分(PD)控制器计算所需加速度。

(54)

在遇到外界干扰时，平衡控制器得到的加速度通过逆运动学控制器反馈到机器人的各个关节力矩中，从而恢复机器人的平衡。其控制过程如图5所示。

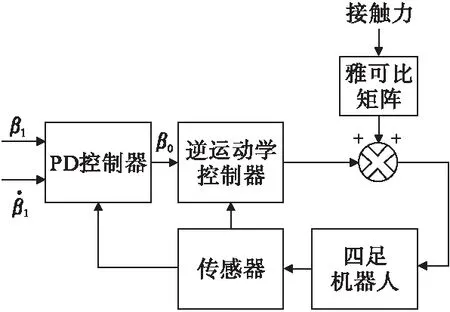
图5 四足机器人控制平衡图

4 仿真与结果

为验证本文提出算法的有效性和优越性，本文利用四足机器人分别在平坦(如图6所示)和不规则地形(如图7所示)进行测试。本次实验的机器人由四条腿和一个主体构成，每条腿有3个自由度，整体自由度为18，机器人可以在环境中沿着坐标系所有坐标轴自由移动。表1为四足机器人各部位特性及控制器参数。

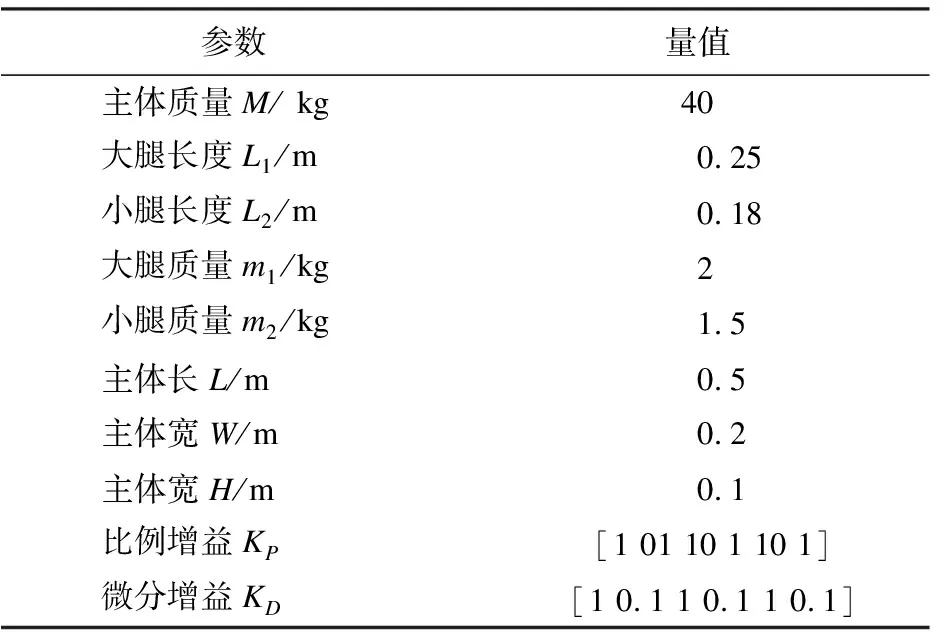
表1 四足机器人各部位特性及控制器参数

平坦地形：

本次实验让机器人沿着X轴行走，如图6所示，机器人在行走中能够非常稳定地从A位置运动到C位置。

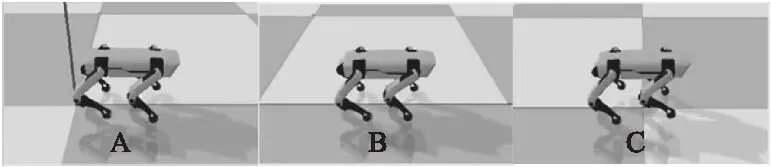
图6 穿越平坦地形

通过图6可知，本文选择的步态和平衡控制器能够很好满足机器人在平坦地形下的行走。

复杂地形：

实验设计了一个凹凸不平的地面，如图7所示，让机器人从A位置开始沿X轴行走至C位置，此时机器人未加平衡控制器。

图7 无平衡控制器穿越不规则地形

通过图7可以看到，在未加平衡控制器时，机器人并不能适应复杂地形，在前进到B位置几欲跌倒，继续行走一小段距离后机器人即已无法保持平衡。可见在不规则地形中，没有平衡控制器的机器人无法适应地形，整个主体部分失去平衡，无法顺利运动到指定地点。

将平衡控制器导入机器人中，重复图7实验，如图8所示。

图8 有平衡控制器机器人穿越不规则地形

由图8可以看出，在加入平衡控制器后，机器人并没有如图7所示那样失去平衡，反而克服了足端所受到的干扰，顺利地从A位置运动到C位置。通过图7、图8对比可以看出，本文设计的平衡控制器能够很好地帮助机器人在不均匀地形行走时维持自身平衡。实验在同一环境下的不同路段进行多次，实验过程中即使四足机器人足端受到各种不同方向的障碍干扰，平衡控制器均能通过获得足端位置向量及时克服环境所带来的干扰。实验表明，该算法在外界干扰下，能及时调整主体位置恢复平衡，并具有一定程度的鲁棒性。

机器人在平坦和不规则地形行走的策略输出如图9所示。

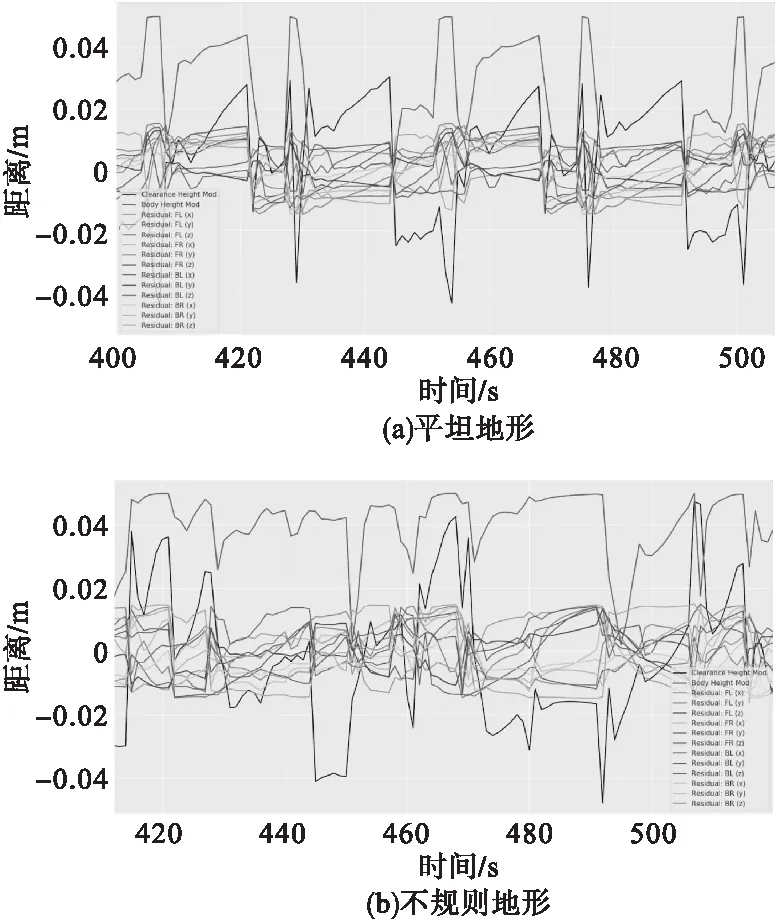
图9 策略输出

由图9a可以看出，当机器人行走在平坦地形时，由于没有受到外界干扰，其身体各部位的策略输出呈一种周期不断循环的状态，所以机器人在行走过程中一直保持平衡状态。由图9b可以看出，当机器人行走在不规则地形中时，其足端一直受到干扰，机器人无法保持平衡；为使机器人保持平衡，平衡控制器不断调节机器人四条腿的扭矩，导致其策略输出不断变化以维持机器人平衡。

5 结论

为实现四足机器人在不规则地形上保持稳定行走，设计了一种基于四足机器人全身动力学的平衡控制器。平衡控制器通过消除机器人足部受到的接触力，将行走时足端反馈的矢量信息通过动力学方程计算，得到平衡所需要的加速度；将加速度通过逆运动学控制反馈到机器人的关节力矩上，实现机器人的稳定控制。在不同的环境下多次仿真表明，该平衡控制器能够有效帮助四足机器人在不规则地形中行走时保持平衡。