过两定点的劣弧圆心角越小弧长越短的应用及证明

摘 要：汽车在弯道转弯行驶时，为使汽车在确定的两点之间匀速行驶的时间最短，在满足汽车速度最大的同时，汽车的运行轨迹必须是经过这两点的长度最小的圆弧;建立关联函数，采用求导方法，用逻辑推理的方式证明，平面内在经过两确定点的劣弧中，劣弧所在圆的半径越大，劣弧所对的圆心角越小，劣弧的长度就越小.

关键词：弯道;匀速行驶;时间最短;函数;求导

中图分类号：G632      文献标识码：A      文章编号：1008-0333（2021）22-0082-02

收稿日期：2021-05-05

作者简介：王伟民（1964-），男，本科，中学高级教师，从事高中物理教学研究.

从一道在多种物理教辅资料动力学板块中常见的题目说起——：

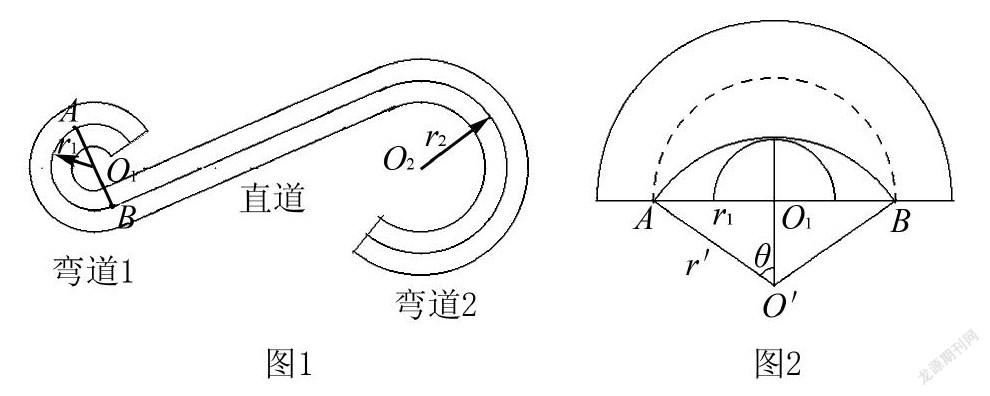
例题1 一段S形单行盘山公路的示意图如图1所示，弯道1、弯道2可以看作两个不同水平面上的圆弧，圆心分别为O1、O2，弯道中心线半径分别为r1=10m和r2=20m，弯道2比弯道1高h=12m，有一直道与两弯道圆弧相切.质量m=1200kg的汽车通过弯道时作匀速圆周运动，路面对轮胎的最大径向摩擦力是车重的1.25倍，行驶时要求汽车不打滑（sin37°=0.6，sin53°=0.8）.（1）求汽车沿弯道1中心线行驶时的最大速度v1;

（2）汽车以v1进入直道，以P=30kw的恒定功率直线行驶了t=8.0s进入弯道2，此时速度恰为通过弯道中心线的最大速度，求直道上除重力以外的阻力对汽车做的功;

（3）汽车从弯道1的A点进入，从同一直径上的B点驶离，有经验的司机会利用路面宽度，用最短时间匀速安全通过弯道，设路宽d=10m，求此最短时间（A、B两点都在轨道的中心线上，计算时视汽车为质点）.

这道题目是不久前有老师在“物理通报”期刊群询问的一道题目.能够发现，该题目涉及的物理问题是一个综合性很强的动力学问题，需要运用到运动学、动力学的多个公式并结合能量转化等相关知识方能解决.图2是参考答案解析中给出的第三个分问题对应的插图，其中汽车运行时间最短的路线是过AB两点并且与轨道内侧圆弧（也就是小⊙O1的圆周）相内切的一段劣弧——即图2中以O′为圆心的劣弧AB.询问者手头有该题目的参考答案，也能看明白参考答案的解析过程，他询问的问题是，如何证明圆弧AB是汽车由A到B最短时间对应的路径？因为教辅资料给出的参考答案的解析，或者網上百度的解析过程，都是直接说图2中与弯道内侧圆弧相内切的劣弧AB的长度是所有过AB两点的劣弧中长度最短的劣弧，但并没有给出证明的过程.

这就是说，过平面内两定点的劣弧，圆弧所对圆心角越小，圆弧所在圆的半径越大，劣弧的长度就越小.

图2中，在弯道路面范围内，以AB为端点可以作无数条劣弧，易知，劣弧所在圆的半径越大，劣弧与弦AB组成弓形的高就越小——将弦长AB视为常量l，可以写出弓形高h与圆弧半径R间的函数关系式，上述结论的正确性性可以通过函数的增减性来进行证明（限于篇幅，这里不再证明）.当弓形高h小到过AB两点的劣弧与轨道内侧圆弧相内切时，汽车运行圆弧轨迹已经到了弯道的内侧边缘，此时汽车运行轨迹圆弧半径最大，汽车不侧滑时对应的速度也达到最大，而此时汽车运行轨迹的长度最小，所以，过AB两点并且与弯道内侧圆弧相内切的劣弧，是汽车由A点驶向B点时间最短的运行轨道.

在上面的推理过程中，我们用到的主要是数学知识，而且过程比较复杂，构造关联函数之后两次求导，利用函数的增减性并结合特殊值间的关系进行论证，作为求解物理问题，这样的做法好像已经偏离了“物理方向”.如果考虑教学的重点和针对性，在物理习题课教学中分析并讲解这道题目时，我们可以跳过证明这一环节，就像参考答案给出的解析过程那样，将“过两定点的劣弧的长度随劣弧所在圆半径的增大而减小”这一规律当成一个“数学定理”直接使用，或者只是在解题过程中增添一句话——可以证明“过两定点的劣弧的长度随劣弧所在圆半径的增大而减小”，其正确性的推证无需体现在解题过程之中.不过，作为教师，在备课过程中还是应该对上述结论进行严密的逻辑论证，毕竟该结论不是“数学定理”，凭感觉进行判断是在犯经验主义错误，而且未必正确，命题的正确性需要逻辑论证的.

参考文献：

[1]漆玉琼.巧用弧的特征解决实际问题例讲[J].数理化解题研究，2020（1）：41-42.

[2]崔建勤.最短路径的作图与探究[J].中学数学教学参考，2016（Z2）：136-137.

[责任编辑：李 璟]