多尺度自卷积变换与MSER组合的影像匹配方法研究

吉长东,沈晓刚

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

影像特征提取与匹配技术作为计算机视觉研究的核心技术之一，一直以来就是相关行业的重点研究方向。在数字图像的处理中，许多关键问题例如图像的分类、检索、目标跟踪、恢复、重建等都可以归结为影像的本质特征提取问题，在特征提取完毕之后，则是进行同名影像的匹配，影像匹配技术是摄影测量中自动空中三角测量的基础，数字表面模型(DSM)、数字高程模型(DEM)、数字正射影像(DOM)，影像的拼接等也需要影像匹配技术的支持;乃至后续的空间数据产品的生产都是与影像匹配技术息息相关的。而影像匹配技术的大力发展，也使得以影像数据为基础的各类技术手段能够在应急指挥、国土安全、智慧城市、数字城市等方面均有广泛应用[1-3]。

最大稳定极值区域(Maximally Stable Extremal Regions,MSER)，在局部特征提取中，常常用来检测影像中的斑点区域，由J.Matas等学者于2002年提出[4]。该算法思想原理简单，提取出的特征区域具有很强的稳定性，并且不需要提前对影像进行任何处理就可以同时检测出具有不同尺度的特征区域。周鹏飞等人利用卷积神经网络提取文本影像中的多特征，与MSER算法进行融合，使得文本定位的准确率大大提高[5]。针对有些特征区域显著性不强的问题，T.Tuytelaars等研究人员对MSER提取的椭圆拟合局部特征区域做出一定程度的扩增，这使得极值区域的特征显著性明显增强，有效提升匹配的精准度[6-7]。但当影像仿射变化加剧时，该算法的匹配性能也会急剧下降。

多尺度自卷积变换(Multi-Scale Auto-convolution，MSA)是一种基于不变矩的特征提取算法[9]，它以多尺度理论为基础，将概率统计学的思想与仿射变换相结合，可以实现多尺度的特征提取，这些特征向量均具有一定的仿射不变性。黄波[10-11]等人在研究全局的仿射不变特征研究中利用MSA算法构建出的关于多尺度自卷积的归一化直方图的特征提取方法，并在计算运行方面利用最小基准变换减少算法中关于傅里叶变换的计算次数，有效的提升了MSA算法的效率。张洁玉[12]则构造出多尺度自卷积熵(MSAE)，与MSA变换进行特征向量融合，作用于局部特征区域，描述符的辨识率有极大的提高。但该类方法的不足在于一个尺度变化只能提取相对应的一个特征，这容易导致特征尺度集过于庞大且计算量巨大。基于此，提出一种将改进的MSA算法作为特征描述符，与MSER特征区域相融合的影像局部匹配算法，并选用两组影像进行算法的可行性验证与分析。

1 MSER局部特征区域检测与筛选

1.1 MSER基本原理与组合算法流程

受分水岭概念思想的启发，即在自然地形中有高低不平的地势地貌，而影像也因每个像元的灰度值的不同类似于地势不一样的地形，当有水注入的时候地势较低的地方就会形成水洼，当水继续注入而水洼的水面大小不再变化时，这个水洼被认为是一个区域不变的地方，算法原理如图1所示。

图1 MSER算法示意图

MSER算法将其运用到影像特征检测上，将原影像进行二值化，影像灰度值在0～255内连续增加或者减少时，在定义的阈值范围内如果连通区域的面积不再有明显的变化，则认为该区域是局部特征不变区域。但MSER算法与分水岭的分割思想还是有所区别的，分水岭算法在做影像分割时其阈值是在不断改变的，这将导致它得出的连通域面积会实时变化，变化也是明显的；而MSER算法所要求的是极大稳定极值区域，因此在做特征区域检测时追求的是局部阈值发生改变时能够使连通域面积的变化率达到极小的状态，即可以认为连通域的面积变化率不再随阈值的改变而有明显变化[13]。

组合算法流程如图2所示。

图2 组合算法流程

先对影像进行MSER局部特征区域检测，将检测到的区域以影像单元格网信息熵为权重进行特征区域数额的分配优化；然后，以MSA的概率密度直方图熵为特征描述向量，对局部特征区域进行描述，利用次邻近匹配算法进行影像的粗配准。最后利用随机抽样一致算法进行误匹配的剔除，以得到正确的同名点匹配。

1.2 MSER局部特征区域筛选

以信息熵作为筛选条件，对影像的MSER局部特征区域进行特征筛选工作，在特征描述之前先剔除部分可能无法被辨识的局部特征区域。

假设影像的MSER检测的特征区域总数为X，并且每一个特征区域都进行了椭圆拟合。将影像平均划分成3×3共9个单元格网影像，根据特征区域中心位置坐标确定特征属于哪一个单元格网影像，并且以每个格网影像的信息对整幅影像做出的贡献量确定各格网影像的特征区域分配数量；影像信息熵的计算方法为：

(1)

式中:H表示影像信息熵；M和N表示的是需要计算信息熵影像区域的高度和宽度，即影像矩阵的行和列；pij是影像中像素点(i,j)的灰度值概率。利用式(1)计算出每个格网影像的信息熵Hk,k∈[1,9]，k为每个单元影像的标号，将9个格网的信息熵相加为HS，那么每个格网影像应该分配的特征数为：

(2)

在每个单元格网内按照特征区域信息熵从大到小的顺序进行排列，单元格网内的特征区域数L小于等于分配额tk，那么该单元格网内的特征数量就为L个；若L大于分配额tk，那么该单元格网内的特征数按照排列顺序取前tk个，即剔除后L-tk个。具体流程如图3所示。

图3 MSER局部特征优化流程

至此，基于信息的特征区域筛选工作结束，此方法可有效去除影像中一些信息量不足特征区域，且对于特征区域的空间分布均衡性更有利，亦能有效提高影像匹配效率。

2 改进的MSA局部特征描述向量

2.1 MSA仿射不变特征提取原理

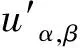
Tuα,β+t.

(3)

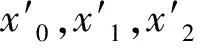
(4)

2.2 MSA灰度概率密度直方图熵

根据MSA特征构造过程分析得出，要获得更多的特征描述需要不断改变尺度(α,β)，且MSA变换对更细微的特征提取能力有限，因此，基于MSA变换构建灰度概率密度直方图熵特征向量。

定义uα,β的概率密度函数：

pUα,β(u)=(pα×pβ×pγ)(u).

(5)

式中:γ=1-α-β；对x，y，u进行仿射变换得到x′=Tx+αt，y′=Ty+βt，u′=Tu+(α+β+γ)t，当α，β，γ均不为0时，将仿射变换前后的概率密度函数引入式(5)，并转化为积分形式：

(6)

由式(6)可以发现，p(x)=|det(T)|p′(Tx+t)，对此进行替代与化简得出仿射变换前后概率密度函数的关系：

(7)

仿射变换中T是未知的，需构造归一化直方图，以此来削弱仿射变换带来的干扰。定义仿射变换前后特征区域的概率密度函数为：

(8)

(9)

显而易见，特征区域归一化灰度概率密度也是仿射不变的，由于影像中的灰度概率密度函数是离散型的，在计算pα,β,γ(u)时要注意将卷积形式改为离散的傅里叶乘积形式即可；为构建直方图仿射不变向量，将灰度区间等分成N份，即(B1,B2,…,BN)，定义在任意一个区间内，有：

(10)

根据式(10)即可构造出在一个尺度(α，β)上的特征区域的归一化仿射不变直方图描述向量：

(pB1,pB2,…,pBN).

(11)

从上述的直方图构造原理可知，特征区域的灰度分布是不变的，那么基于归一化直方图的熵也是不变的，对此，可以根据直方图构造基于直方图的熵仿射不变向量：

(12)

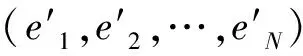
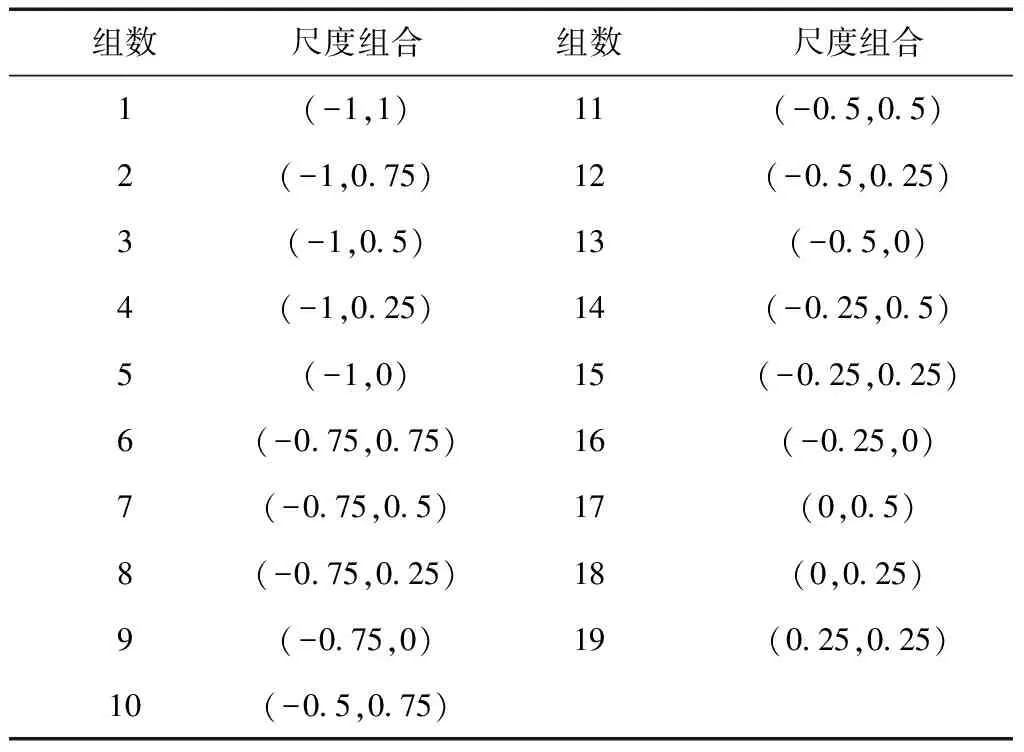
表1 尺度集

该向量主要从局部区域灰度直方图特征分布的不确定性来对影像进行描述，此特征提取方法不仅具有仿射不变性，而且相对于MSA算法具有更好的鲁棒性以及更高的描述精度。

3 实验结果与分析

为验证所阐述的方法在影像发生不同程度的仿射变换时的有效性，设置两组对比实验，将本文算法与MSER算法进行实验对比和性能比较分析。数据来源为著名学者Krystian Mikolajczyk提供的具有仿射变换的近景影像，共有两组数据：wall影像组(见图4)和graf影像组(见图5)，每组影像集中含有6张仿射变换影像。

为筛选出含有高信息量的局部特征区域，提高匹配效率，增加局部特征区域向量描述的质量与可区分性，首先进行MSER局部区域的特征筛选实验，部分影像实验结果如图6所示。

图7为对两组影像数据的筛选情况做出比对情况，横坐标为影像名，纵坐标为每幅影像中的特征区域数量，蓝色线表示筛选前，红色线表示筛选后，关于影像匹配实验，影像匹配的效果一般需要对其进行定量分析和评价，论文采用推定匹配率和误匹配率对上述局部特征提取算法进行性能评价。定义影像检测特征数量为nF，总匹配对数为nall，正确匹配数为ncor，则：

推定匹配率：

(13)

准确率：

(14)

式中：nF1和nF2为参考影像和带配准影像的特征检测数量。

图4 wall影像组数据

图5 graf影像组数据

首先对各组实验数据做影像粗匹配处理，由于篇幅有限，下面关于影像的匹配效果仅展示本文算法匹配的一部分，对MSER算法匹配效果不再展示。图8和图9为部分实验结果图，视图左半部分为每组影像的参考影像，视图右半部分为待配准影像。

为得到正确的同名点匹配，实验以随机抽样一致性算法(Random Sample Consensus,RANSAC)作为误匹配剔除算法，剔除粗匹配中含有的错误同名点对。

图10和图11为部分实验结果图，视图左半部分为每组影像的参考影像，视图右半部分为待配准影像。

图6 影像特征区域筛选前后效果对比

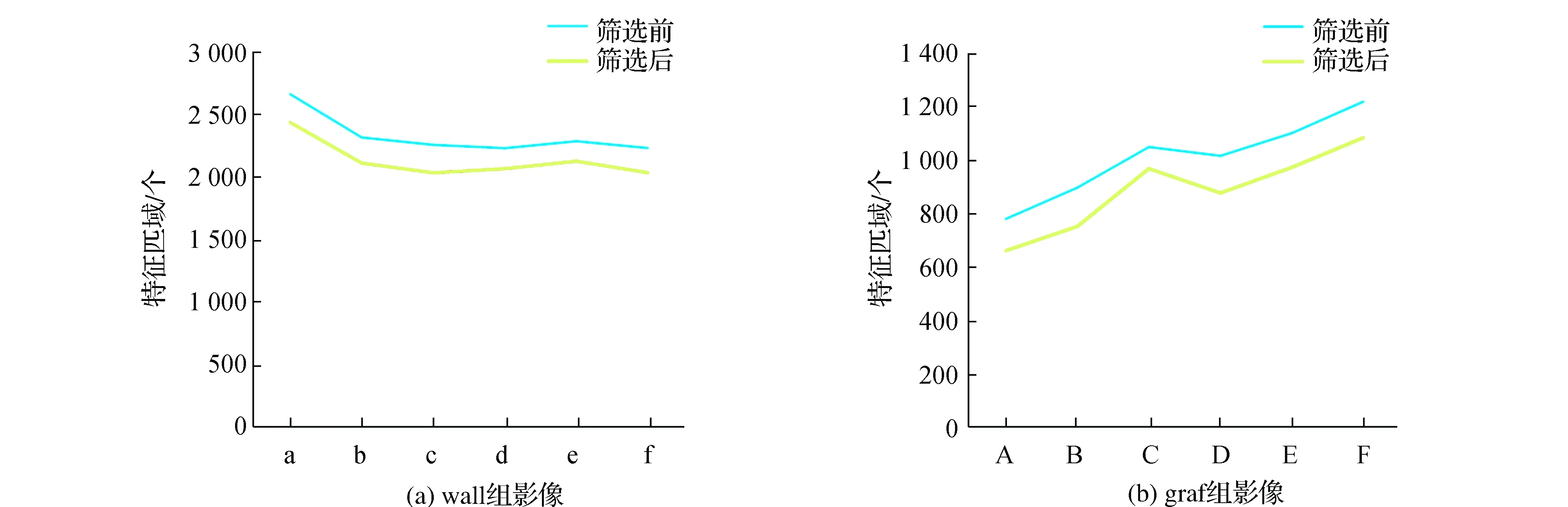
图7 影像特征区域筛选前后对比

图8 wall(a)和(e)粗匹配(组合算法)

特征粗匹配详细的实验结果由图12的影像粗匹配数量统计直方图给出，蓝色表示为组合算法结果，红色为MSER算法实验结果。

去除误匹配详细的实验结果由图13的影像精匹配数量统计直方图给出，蓝色表示为组合算法结果，红色为MSER算法实验结果。

图9 graf(a)和(e)粗匹配(组合算法)

图11 graf(a)和(e)精匹配(组合算法)

图12 graf影像两种算法特征粗匹配

对于本文提出的组合算法评价，采用影像推定匹配率和准确率来进行定量分析，蓝色表示本文提出的组合算法，红色表示MESR算法，图14计算的是3组影像本文算法与MSER算法的推定匹配率，图15所表达的是组合算法与MSER算法的匹配正确率。

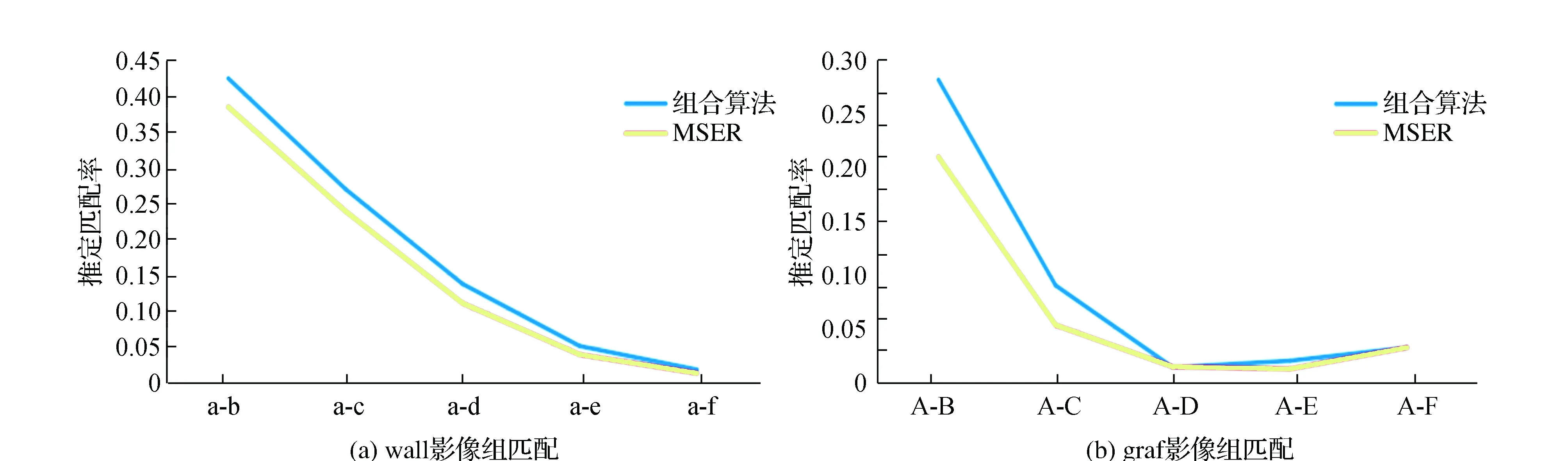
图14 影像推定匹配率

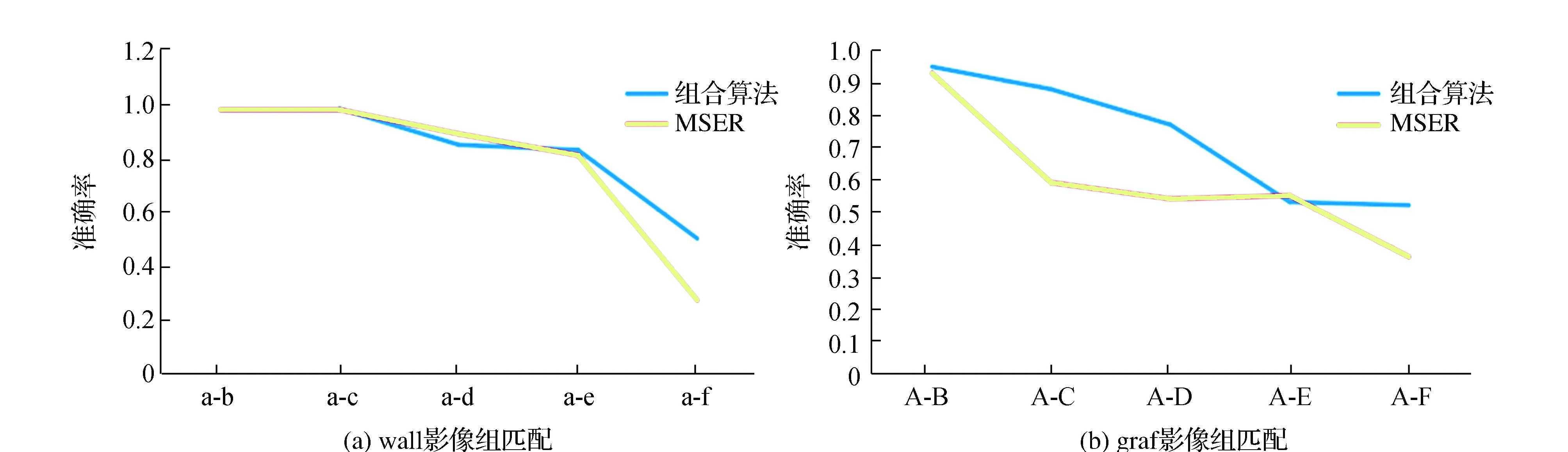
图15 影像组匹配准确率

4 结 论

为了提高影像的几何仿射变换而导致的特征检测与匹配效果不理想的问题，从影像全局特征提取与局部特征检测方面进行研究，提出一种将MSA灰度概率密度直方图熵提取方法与MSER优化特征区域检测方法组合的算法。根据实验验证得出如下结论：

1)针对局部特征区域数量较多而造成匹配效率低的问题，采用信息熵原理对局部区域进行优化筛选，综合两组实验数据来看，在本文实验中特征区域平均有11%左右被认为是不合格的，不仅提升特征描述的效率，也使特征描述向量的可区分性更强。

2)针对常用局部特征匹配算法仿射不变特征提取能力不强的问题，提出将MSA灰度概率密度直方图熵作为仿射不变特征描述符，对优化后的MSER局部区域进行特征描述，通过匹配实验发现，在大多数情况下，无论是推定匹配率还是匹配准确率，本文提出的组合算法要优于MSER算法，在wall组影像试验中，两种算法的差异性体现的不是很明显，但在graf影像组实验中，两种算法的差异性是显然的。这也证明提出方法的仿射不变性也更强，匹配效率更高。