2种吸附模型下非饱和土中污染物迁移规律分析

2021-09-13罗玚,蒲育

兰州工业学院学报 2021年4期

罗玚,蒲育

(兰州工业学院土木工程学院,甘肃兰州 730050)

0 引言

我国是一个土地资源匮乏的国家,近年来随着我国经济的高速发展和城市规模的不断扩大,工业和生活污水对地表土体的污染在不断加重,在农业生产领域,由于农药和化肥的大量使用也造成土体的不同程度污染,各种污染物在大气降水等因素的作用下向土体深部迁移传递,影响地下水水质,同时在力、光照、温度等因素的耦合作用下,形成聚集,使土体盐渍化,进而造成土体承载力下降,引起一系列工程问题,要解决这些问题的前提是研究土体中污染物的迁移规律.

国内外众多学者对污染物在土体中的迁移问题进行了大量研究.理论方面,傅臣家等[1]对饱和土体中铬元素的吸附、迁移规律进行土柱试验并运用Hydrus-1D软件进行建模模拟;位菁等[2]以2个典型工业固体废弃物堆场为研究对象,运用数值模拟软件Modflow对主要金属离子在雨水淋滤作用下在地下水系统中的迁移进行模拟计算,对金属离子的迁移范围、浓度变化进行了研究,确定了堆场可能污染到的区域和程度;王超等[3]建立了水分和污染物之间耦合迁移的理论模型,并通过有限差分法对污染物在非饱和分层土中的迁移特性进行了研究;刘松玉[6]在考虑渗流作用的基础上建立了一维非饱和土体中污染物迁移的理论模型,讨论了随机降雨条件对土体中污染物浓度分布产生的影响.试验方面,张志红等[10]采用柔性壁渗透仪,通过室内试验研究了混合重金属离子共存情况下侵蚀饱和黏性土的渗透特性变化规律.

综上所述,目前对于污染物在土体中的迁移研究主要以对流-弥散方程为基础,结合试验结果,研究在水-热-浓度耦合作用下污染物的传递迁移规律,但关于污染物分子或离子在静电作用下与土体颗粒吸附问题的文献较少,尤其是对土体吸附污染物的两种典型模型特点的讨论更少有报道.

本文以污染物在液固2相中的质量守恒为基础,建立一维状态下非饱和土体中污染物迁移微分方程,利用数值方法计算考虑土体对污染物的等温线性平衡吸附和等温非线性平衡吸附两种吸附模型下,污染物在非饱和土体中的浓度变化规律,比较2种吸附模型的差异,为研究污染物在土体中迁移提供一定参考.

1 数学模型

1.1 污染物质量守恒方程

本文不考虑污染物的分解和降解作用,一维状态下非饱和土体中污染物质量守恒方程为

(1)

1.2 吸附效应

土体对污染物的吸附效应实质是固相与液相的污染物质量交换,将等温状态下污染物吸附处于瞬时平衡的状态称为等温平衡吸附,若等温平衡吸附中固相污染物浓度与液相污染物浓度成正比,则等温吸附线为1条直线,这种吸附模型称为等温线性平衡吸附模型,即Henry吸附模型,数学表达式为

Cs=KC,

(2)

式中:K为吸附系数;Cs为污染物固相浓度;C为液相污染物浓度.

王洪涛[4]在相关文献中介绍了另一种吸附模型,即等温平衡吸附中固相浓度与液相浓度成非线性关系,这种吸附模型称为等温非线性平衡吸附模型,即Freundlich吸附模型,表示为

Cs=KCN,

(3)

式中:N为常数.

分析可知当N=1时Freundlich非线性吸附模型将退化为Henry线性吸附模型,2种吸附模型示意如图1所示.

图1 吸附模型

将式(2)、(3)分别代入Is后得到Henry吸附模型和Freundlich吸附模型下污染物在土体中的迁移微分方程分别为

(4)

(5)

1.3 求解条件

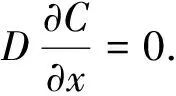
1.4 计算参数

模型中参数取值如表1所示.

表1 模型中参数取值

2 2种模型计算比较

本文研究高度为20 cm的土柱,在顶部施加固定浓度值为C0的污染源,利用Comsol Multiphysic有限元软件,分析2种不同吸附模型下土柱不同位置处污染物浓度变化.本文选取3个点的浓度变化曲线,3个点的位置依次为距离土柱底面1、10、19 cm,3个点的编号依次为1、2、3点.

2.1 污染物空间分布

通过计算得到2种吸附模型条件下土柱中不同时刻污染物空间分布云图,如图2～3所示.

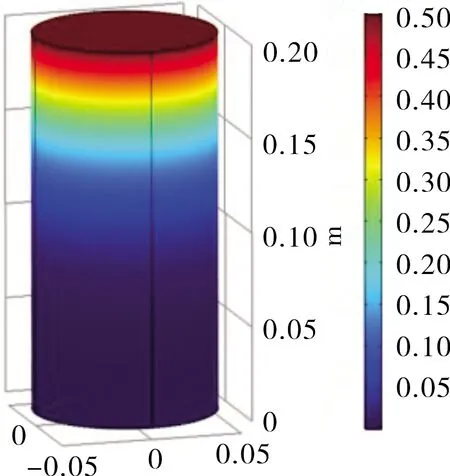
(a) 10 h

(b) 40 h

(a) 10 h

2.2 各点浓度随时间变化曲线

土柱底部从下到上3个点处在2种不同吸附模型下浓度随时间的变化曲线如图4～6所示.

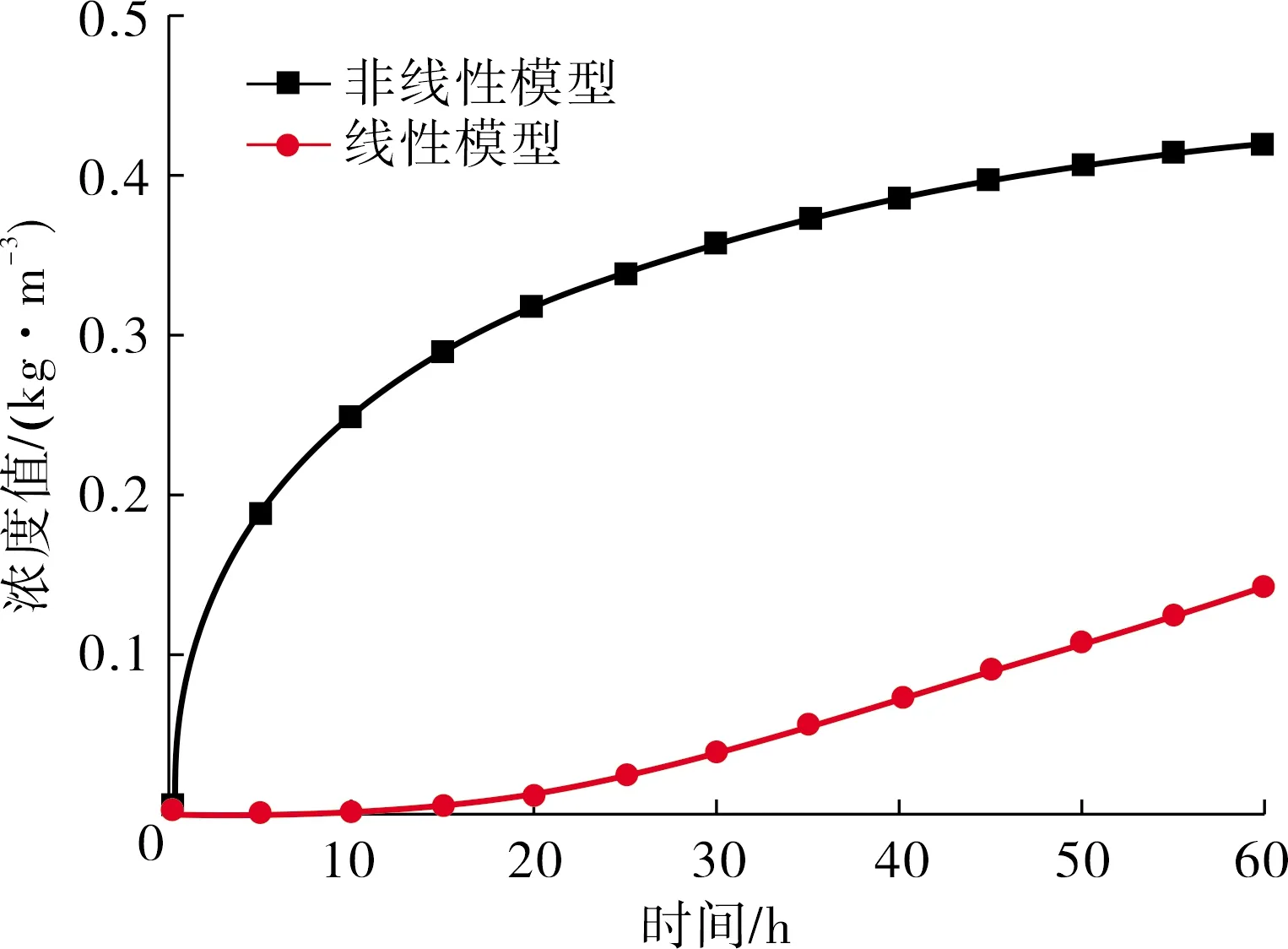
图4 1点浓度变化

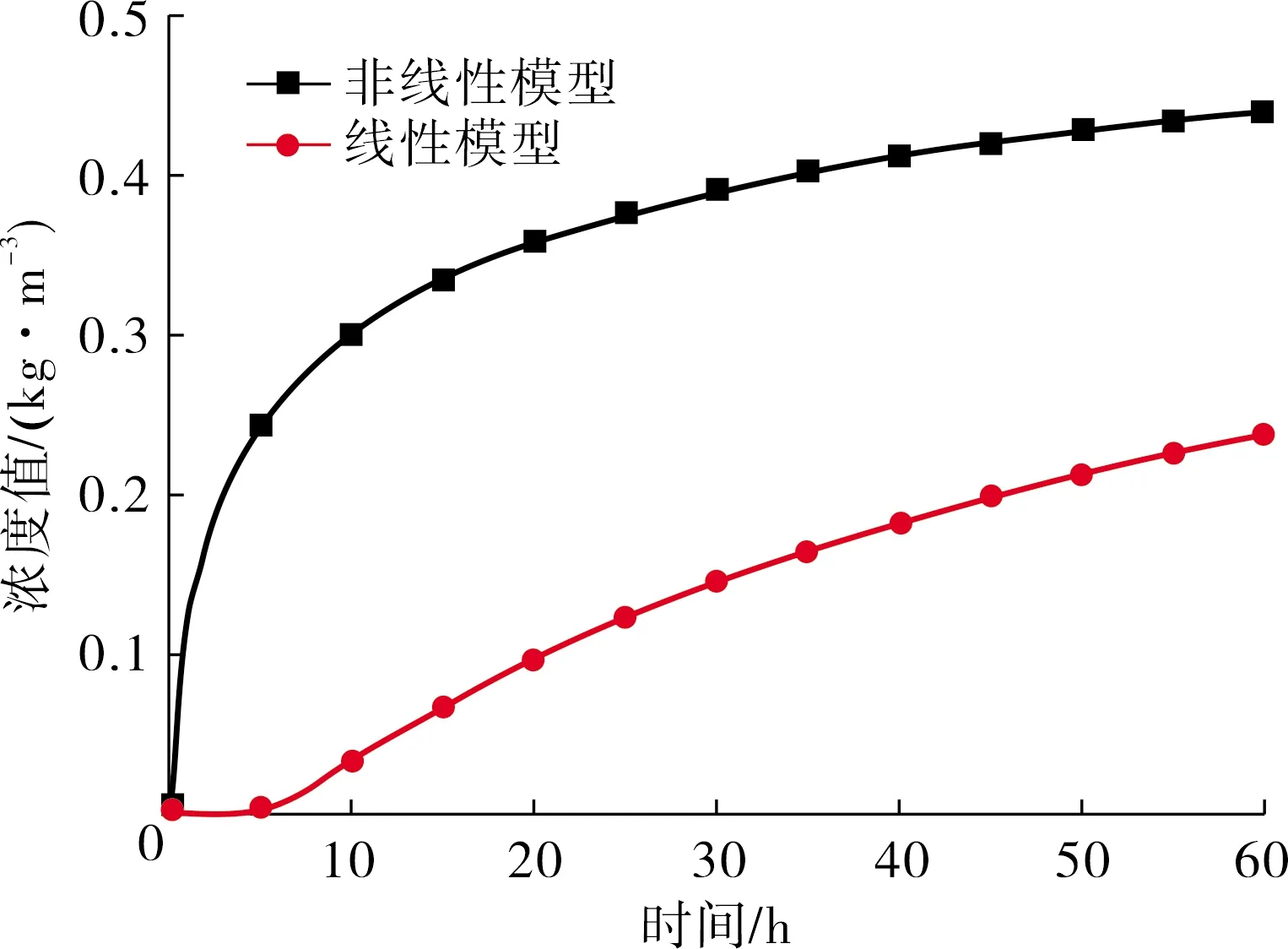
图5 2点浓度变化

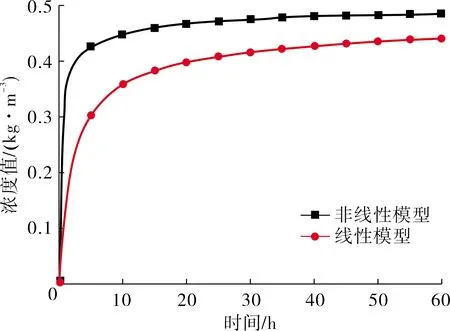
图6 3点浓度变化

观察图4～6可以看出:对于靠近土柱顶面的3点,当污染源输入污染物60 h时,非线性模型下浓度计算值为0.486 kg/m3,线性模型下浓度计算值为0.441 kg/m3,非线性模型结果是线性模型结果的1.1倍,对于土柱中部的2点,非线性模型下浓度计算值为0.439 kg/m3,线性模型下浓度计算值为0.249 kg/m3,非线性模型结果是线性模型结果的1.76倍,对于土柱底部的1点,非线性模型下浓度计算值为0.417 kg/m3,线性模型下浓度计算值为0.14 kg/m3,非线性模型结果是线性模型结果的2.98倍.

综上所述,2种不同吸附模型下3个点处的浓度数值都随着时间的增长而增加,但不同位置处浓度增加幅度有较大差异,靠近土柱顶面,两种模型计算结果比较接近,差别仅为10%,但越靠近土柱下部,差别越来越大,在土柱底部,差别增大到了2.98倍,这也证明了同等条件下,线性模型能够将更多的污染物吸附在土体颗粒周围,从而使土体孔隙中溶液的污染物浓度降低.

2.3 浓度沿土柱高度变化曲线

土柱底部从下到上3个点处在2种不同吸附模型下浓度随时间的变化曲线见图7～9.

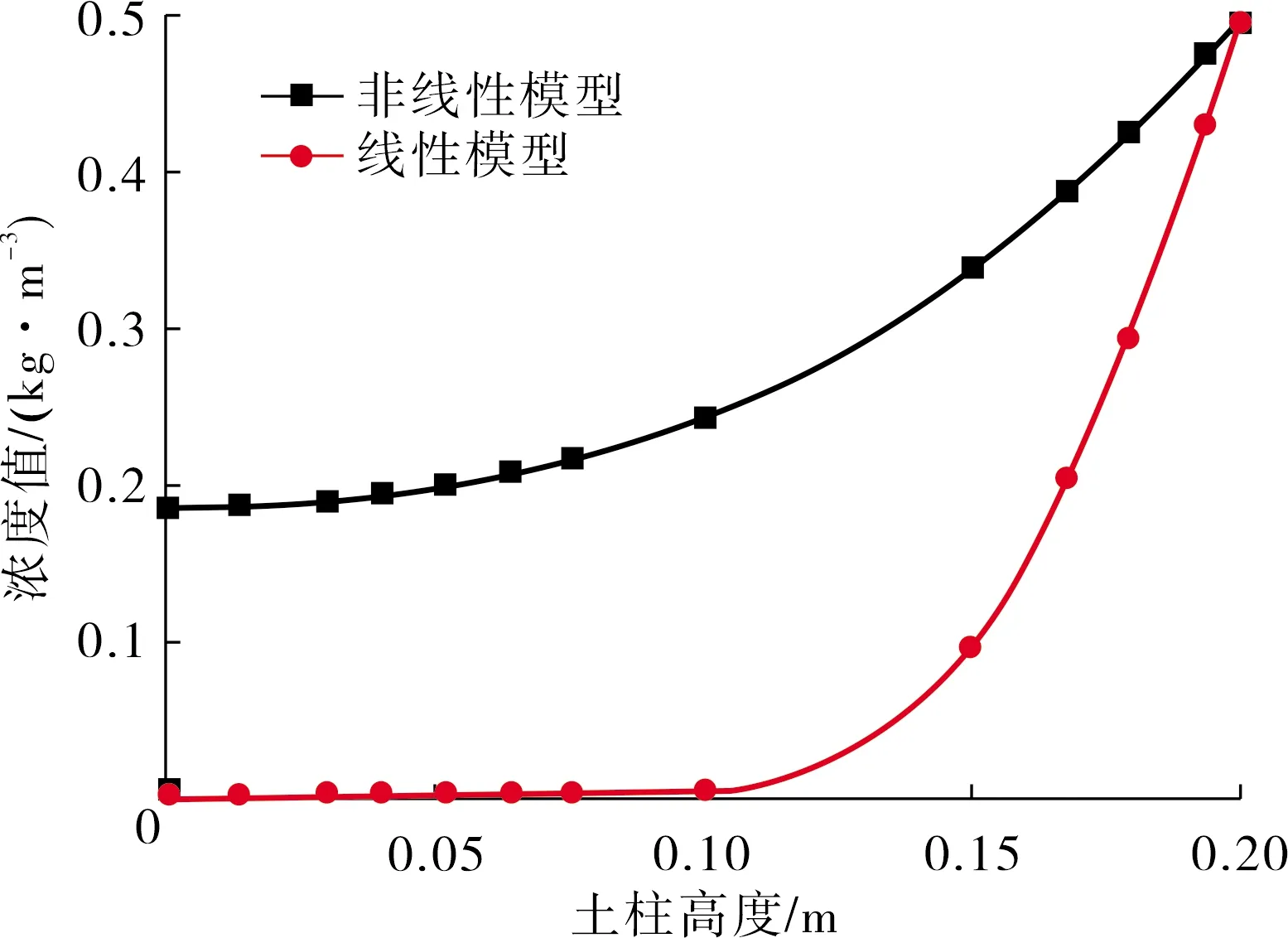
图7 5 h沿土柱高度的浓度变化曲线

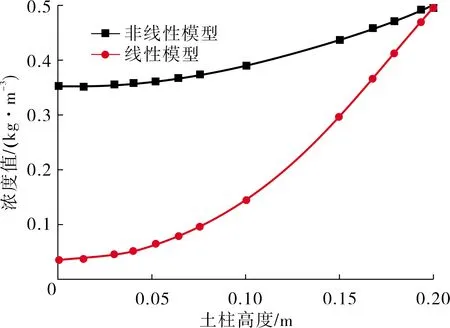
图8 30 h沿土柱高度的浓度变化曲线

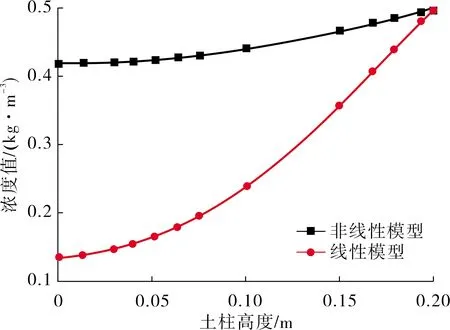
图9 60 h沿土柱高度的浓度变化曲线

观察图7～ 9可以看出:沿土柱高度方向,当污染源输入污染物5 h时,线性模型下土柱中部以下位置浓度计算值近似为0,中部位置浓度计算值为0.053 kg/m3,而5 h时非线性模型下土柱底部位置浓度计算值已经达到0.185 kg/m3,中部位置浓度计算值达到0.244 kg/m3,是线性模型中部位置计算结果的4.6倍;当污染源输入污染物30 h时,线性模型下土柱底部位置浓度计算值为0.036 kg/m3,非线性模型下土柱底部位置浓度计算值为0.35 kg/m3,是线性模型计算结果的9.72倍,线性模型下中部位置浓度计算值为0.147 kg/m3,非线性模型下中部位置浓度计算值为0.39 kg/m3,是线性模型结果的2.65倍;60 h时,线性模型下土柱底部位置浓度计算值为0.136 kg/m3,非线性模型下土柱底部位置浓度计算值为0.417 kg/m3,是线性模型计算结果的3.06倍,线性模型下中部位置浓度计算值为0.239 kg/m3,非线性模型下中部位置浓度计算值为0.44 kg/m3,是线性模型结果的1.84倍.

综上所述,在不同时间点,沿土柱高度方向,非线性模型计算结果都大于线性模型计算结果;非线性模型计算结果与线性模型计算结果的比值沿土柱高度方向从高到低逐渐增大,在土柱底部,非线性模型计算结果是线性模型计算结果的将近10倍,这也再次证明了同等条件下,线性模型吸附效果大于非线性模型.