一种新的犹豫模糊粗糙近似算子的公理刻画
2021-09-13米据生
刘 文 米据生 孙 妍
1(河北师范大学数学科学学院 石家庄 050024) 2(北京理工大学数学与统计学院 北京 100081)
波兰数学家Pawlak[1]于1982年首次提出粗糙集理论,在其研究中,近似算子的定义主要有2种方法:构造性方法和公理化方法.在构造性方法中,多以论域上的二元关系、划分、覆盖、邻域系统、布尔子代数等作为原始概念,并应用这些概念构造近似算子.相反地,在公理化方法中,则把一对抽象的集合值算子作为原始概念,利用一组公理描述上、下近似算子,即首先通过满足某些条件的公理形式给定粗糙集代数系统中的集合算子,其次寻找合适的二元关系使得由该二元关系及其生成的近似空间按构造性方法导出的近似算子恰好就是由公理方法定义的集合算子.
在对粗糙集理论研究的过程中,最早由Lin等人[2]提出了公理化的方法,Yao[3]与Thiele[4]给出了对于一般关系和各种特殊关系下的粗糙近似算子相对完整的公理刻画结果.Wu等人[5]把一般二元关系的粗糙近似算子的公理集拓展到无限论域中.
作为用来处理模糊性和不确定性知识的另一种数学工具,模糊集理论由美国控制论专家Zadeh[6]于1965年首次提出,之后粗糙集与模糊集的融合问题成为热门研究方向[7-8].在模糊粗糙集的研究中,Morsi等人[9]最早使用公理化方法研究模糊近似算子,Yang等人[10]考虑了分别由一般犹豫模糊关系和串行的、自反的、对称的、传递的犹豫模糊关系导出的犹豫模糊粗糙近似算子的公理刻画问题.Wu等人[11]还给出了对偶(S,T)-模糊粗糙近似算子的单公理刻画,Zhang等人[12]给出基于覆盖的近似算子的公理刻画,Pang等人[13]基于3类新的L-模糊关系给出了L-模糊粗糙近似算子的公理刻画,Pang等人[14]提出了一个L-模糊近似算子的一般结构和各种类型的L-模糊粗糙集,并用单个公理刻画了每一类L-模糊关系及其组合对应的L-模糊近似算子.Li等人[15]提出了一种基于模糊邻域系统的粗糙集模型并从公理化的角度研究了粗糙近似算子.对于完全分配格L,Sun等人[16]引入了L-模糊上近似算子的概念,给出了L-模糊上近似算子的公理刻画,并讨论了串行的、自反的、一元的和传递的L-广义模糊远邻域系统产生的L-模糊上近似算子的性质.对于剩余格L,Wang等人[17]进一步研究了L-模糊粗糙集的公理刻画,并用2种不同的方法研究了L-模糊粗糙上近似算子的单公理刻画问题.Pang等人[18]针对L是一个完备的Heyting代数的情形,给出了L-粗糙近似算子的一般结构.在公理化方法中,证明了分别与串行的、自反的、对称的、传递的、欧几里德的等多种L-关系所生成的每一类L-粗糙近似算子,都可以用一条公理来刻画.
在犹豫模糊粗糙集理论研究中,Yang等人[10]提出的模型存在一个问题:2个犹豫模糊集之间的包含关系不一定是反对称的,即对任意2个犹豫模糊集A和B,若A⊆B且B⊆A,则不一定有B=A成立.针对这一问题,Zhang等人[19]将Yang的模型进行改进,提出了一种新的犹豫模糊粗糙集模型.本文基于文献[19]所提出的新模型给出犹豫模糊粗糙近似算子的公理刻画.
1 基础知识
本节给出犹豫模糊集、犹豫模糊关系、犹豫模糊粗糙集的相关概念和性质.
定义1[10].设U为非空有限论域,U上的一个犹豫模糊集定义为A={〈x,hA(x)〉|x∈U},其中hA(x)为x在犹豫模糊集合A中的隶属函数,即hA(x)是[0,1]中不同值的有限集合,表示U中元素x在犹豫模糊集合A中的可能隶属度.
方便起见,称hA(x)为犹豫模糊元,U上所有犹豫模糊集构成的集合称为U的犹豫模糊幂集,记为HF(U).
注意到,不同犹豫模糊元中数值的数目可能不同,记l(hA(x))表示hA(x)中数值的个数,为了方便计算,给出2点假设:
1)将每个犹豫模糊元中的元素按递增顺序排列,记为
其中k表示递增排列后犹豫模糊元中第k个数值.
2)为了方便计算以及合理地对2个犹豫模糊元hA(x)与hB(x)进行比较,则当l(hA(x))≠l(hB(x))时,这2个犹豫模糊元需要有相同的长度.令
l=max{l(hA(x)),l(hB(x))},
并将元素较少的犹豫模糊元进行扩充,直到l(hA(x))=l(hB(x))=l.在乐观准则下,通过重复添加最大值进行扩充;在悲观准则下,通过重复添加最小值进行扩充.
由于文献[10]中提出的犹豫模糊粗糙集模型中任意2个犹豫模糊集之间的包含关系不一定是反对称的,然而在经典集合理论中任意2个集合间的包含关系都满足反对称性.为了弥补这一问题,文献[19]将Yang等人[10]的模型进行了改进,重新定义了2个犹豫模糊集合间的包含关系.
定义2.设U为非空有限论域,A,B为2个犹豫模糊集,若hA(x)⪯hB(x),∀x∈U,其中
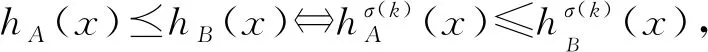
则定义为A⊆B.
显然上述包含关系满足反对称性.
定义3[20].设U为非空有限论域,称R∈HF(U×U)为U上的犹豫模糊关系.
若∀x∈U,∃y∈U使得hR(x,y)={1},则称R是串行的;
若∀x∈U都有hR(x,x)={1},则称R是自反的;
若∀(x,y)∈U×U都有hR(x,y)=hR(y,x),则称R是对称的;
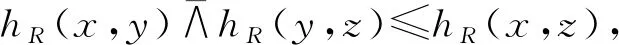
对于∀x,y,z∈U都成立,则称R是传递的,其中k=1,2,…,l,l=max{l(hR(x,y),l(hR(y,z)),l(hR(x,z))};
若R满足自反性、对称性和传递性,则称R为等价的犹豫模糊关系.
基于犹豫模糊元之间新的运算法则,文献[19]提出一种新的犹豫模糊粗糙集模型.在该模型当中任意2个犹豫模糊集之间的包含关系一定是反对称的.
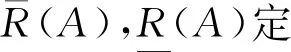
其中



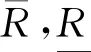

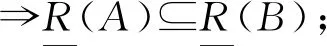
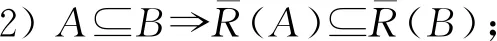
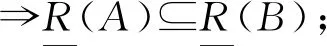
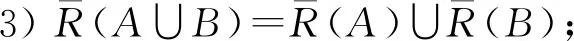
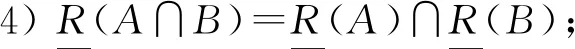
其中∀A,B∈HF(U),∀ai∈[0,1],i=1,2,…,m,C(a1,a2,…,am)表示取值为{a1,a2,…,am}的犹豫模糊常数集.

1)犹豫模糊关系R是串行的
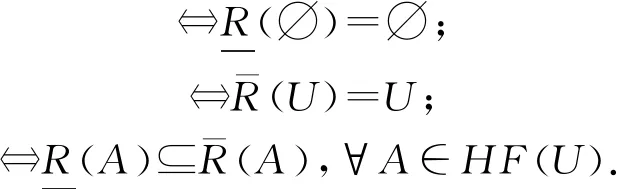
2)犹豫模糊关系R是自反的
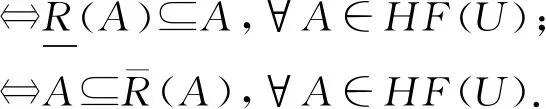
3)犹豫模糊关系R是对称的
4)犹豫模糊关系R是传递的
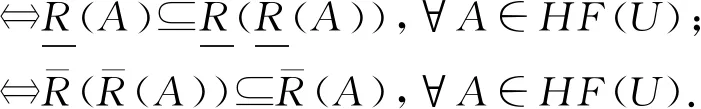
2 犹豫模糊粗糙近似算子的公理刻画
本节首先给出由一般犹豫模糊关系导出的犹豫模糊粗糙近似算子的公理刻画.
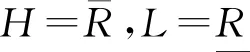



其中I为任意索引集.再由性质1得:
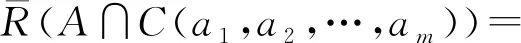
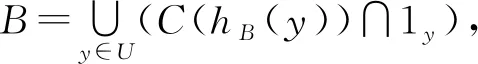
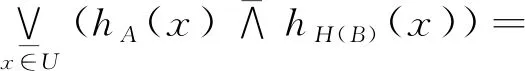
其次证明必要性.设犹豫模糊集合算子H满足(HFU),由H定义U上的犹豫模糊关系R为
hR(x,y)=hH(1y)(x),∀(x,y)∈U×U.
注意到∀A∈HF(U),∀x∈U,都有:
则∀B∈HF(U)根据定义4可知:

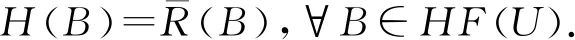
对于下近似算子的情形,由L定义U上的犹豫模糊关系R为
hR(x,y)=hL(U-{y})(x),∀(x,y)∈U×U.
同时∀A∈HF(U),注意到
即可证明.
证毕.
下面研究由串行的、自反的、对称的、传递的和等价的犹豫模糊关系所生成的犹豫模糊粗糙近似算子的公理刻画.
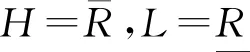
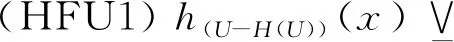



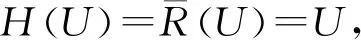
因此根据定理2得:
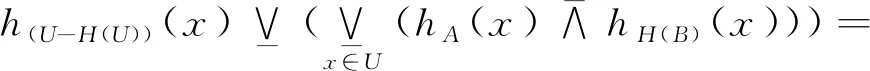
其次证明必要性.设H满足(HFU1),取A=∅,根据(HFU1)则有:
因此:
h(U-H(U))(x)=0⟹(U-H(U))=∅
⟹U=H(U).
所以:
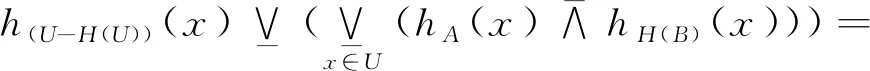

证毕.
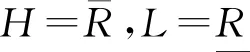

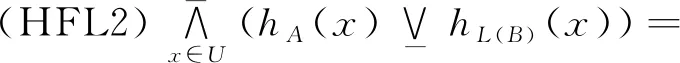



因此根据定理2得:
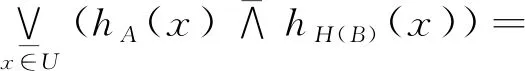
其次证明必要性.设犹豫模糊集合算子H满足(HFU2),则:

因此H(B)=B∪H(B),这样B⊆H(B).
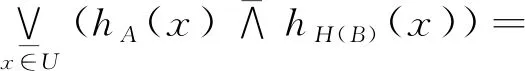
由(HFU2)可知:
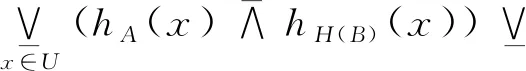
因此:
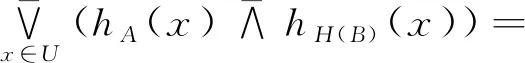
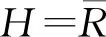
证毕.
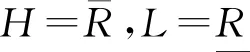
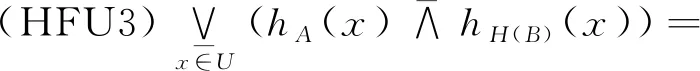
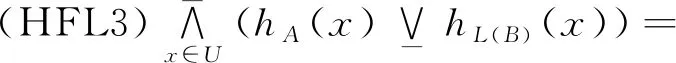

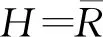
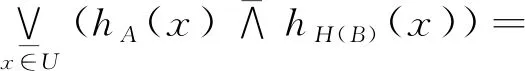
其次证明必要性.设H满足(HFU3),
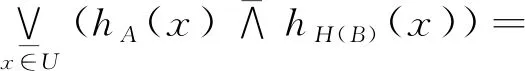
取B=1y,A=U则有:

因此hH(1y)(x)=hH(1x)(y).所以
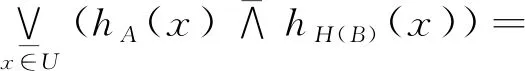

证毕.
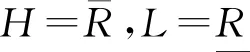




∀B∈HF(U).因此根据定理2得:
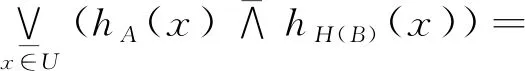
其次证明必要性.设犹豫模糊集合算子H满足(HFU4),则
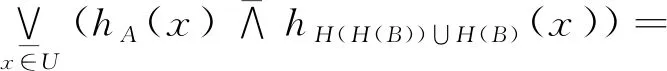
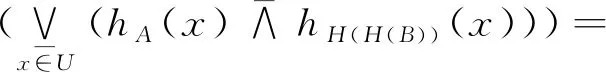

因此H(B)=H(H(B))∪H(B),这样
H(H(B))⊆H(B).
于是:
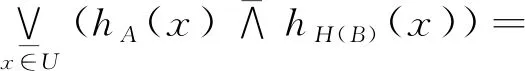
由(HFU4)可知:

因此:
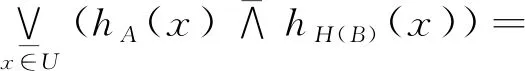

证毕.
综合定理4~6并根据定义3即可得到定理7.
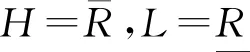
3 犹豫模糊拓扑空间的诱导
利用第2节所给出的各类犹豫模糊粗糙近似算子公理刻画的结论,对犹豫模糊粗糙近似空间与犹豫模糊拓扑空间之间的关系进行研究.由于近似算子的对偶性,下面仅对犹豫模糊下近似算子进行讨论.
推论1.设U为非空有限论域,R为U上一个自反且传递的犹豫模糊关系,则有等式成立:
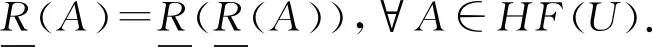
证明.由定理4和定理6可知,R满足:
(1)
(2)

证毕.
在文献[19]中已经证明了U上一个自反且传递的犹豫模糊关系R满足:
其中∀Aj∈HF(U),J为索引集.
下面证明U上自反且传递的犹豫模糊关系在U上能诱导一个犹豫模糊拓扑空间.
定理8.设U为非空有限论域,若R为U上的自反且传递的犹豫模糊关系,则存在U上的一个犹豫模糊拓扑τR,使得
由文献[21]中犹豫模糊拓扑的定义可知,(U,τR)为犹豫模糊拓扑空间只需满足:
1)C(a1,a2,…,am)∈τR,其中{a1,a2,…,am}⊂[0,1],C(a1,a2,…,am)表示犹豫模糊常数集.
2)A∩B∈τR,∀A,B∈τR.

证明.
1)由自反性易知该犹豫模糊关系是串行的,因此
因此C(a1,a2,…,am)∈τR.

因此A∩B∈τR.

证毕.
4 结束语
本文基于文献[19]所提出的新的犹豫模糊粗糙集模型进行研究,得出刻画犹豫模糊粗糙近似算子的一种新公理集.并进一步解决了分别由串行的、自反的、对称的、传递的和等价的犹豫模糊关系所生成的近似算子的公理刻画问题.最后应用本文结论证明了由犹豫模糊粗糙近似空间可以诱导出一个犹豫模糊拓扑空间.
本文所给出的犹豫模糊粗糙集的公理化方法比较简洁地刻画了犹豫模糊粗糙集的数学结构.另外,由于粗糙集理论中的下近似算子和上近似算子与模态逻辑学中的必然性算子和可能性算子、拓扑空间中的内部算子和闭包算子、Dempster-Shafer证据理论中的信任函数与似然函数都有密切联系,因此将粗糙集理论推广到犹豫模糊环境下,可以揭示犹豫模糊粗糙近似算子更深层次的本质特点,且为进一步探讨犹豫模糊粗糙集的拓扑结构奠定基础.
