一种双层贝叶斯模型：随机森林朴素贝叶斯

张文钧 蒋良孝,2 张 欢 陈 龙

1(中国地质大学计算机学院 武汉 430074) 2(智能地学信息处理湖北省重点实验室(中国地质大学) 武汉 430074)

近年来，随着互联网信息的指数式增长，如何将海量的文本数据按照指定的类别自动归类，已成为自然语言处理的一项重要研究任务[1].为解决复杂的文本数据带来的独特挑战[2]，已有许多经典的机器学习方法被用来解决文本分类问题，比如朴素贝叶斯、支持向量机、K近邻、决策树等.

朴素贝叶斯模型因其简单、高效、易理解的特点被广泛应用于文本分类任务.在处理文本分类任务时，文档的特征通常用其中出现的单词来表示.按照单词在文档中是否出现，可将每个单词看作一个布尔变量，由此构建的朴素贝叶斯模型称为多变量伯努利朴素贝叶斯模型(Bernoulli naive Bayes,BNB)[3].BNB只考虑单词在文档中是否出现，而完全忽略了单词在文档中出现的频次信息.为了弥补BNB所面临的这一不足，McCallum和Nigam[4]提出了多项式朴素贝叶斯分类模型(multinomial naive Bayes,MNB)，在分类过程通过捕获单词在文档中的出现频次来获得更好的分类性能，因此MNB较之于BNB有更加广阔的应用前景.

不过MNB与BNB都存在一个共同的不足：其属性条件独立假设在面对复杂的文本数据时往往很难得到满足.因此，削弱朴素贝叶斯文本分类模型所要求的属性条件独立假设成为改进朴素贝叶斯文本分类模型的重要途径.为此，学者们提出了许多改进方法，概括起来主要包括结构扩展[5]、实例选择[6-7]、实例加权[8]、特征选择[9-10]、特征加权[11-15]等.相关的实验研究也验证了这些方法的有效性.

然而，所有这些方法都是基于原始的单词特征来构建分类模型，由于朴素贝叶斯模型假定单词之间相互独立，因此在分类中很难学习到多个单词组合在一起时对分类的影响.然而现实情景中单个的单词特征携带的信息有限，单词组合在一起才可以表达更多的语义信息.基于当前朴素贝叶斯文本分类模型的这一局限，本文尝试用特征学习的方法，从原始的单词特征中学习到由多个单词特征组合在一起表示的高层特征，再基于学到的高层特征训练朴素贝叶斯模型.基于这个想法，本文提出了一种双层贝叶斯模型：随机森林朴素贝叶斯(random forest naive Bayes,RFNB)，以改进朴素贝叶斯文本分类模型的分类性能.RFNB分为2层，在第1层采用随机森林做特征学习，利用Bagging集成的优势以及随机决策树的随机性从原始的单词特征中学习多个单词特征组合在一起表示的高层特征，构成新的特征表示.学到的新特征输入第2层，经过一位有效编码(one-hot encoding)后用于构建伯努利朴素贝叶斯模型.

本文的主要贡献包括2个方面：

1)对朴素贝叶斯文本分类模型进行较为全面的调查研究，总结了朴素贝叶斯文本分类模型的5类改进方法；创新性地提出了改进朴素贝叶斯文本分类模型的特征学习新方法，构建了一种双层贝叶斯模型——随机森林朴素贝叶斯(RFNB)，设计并实现了学习RFNB模型的新算法.

2)针对朴素贝叶斯文本分类模型假定单词特征之间完全独立的不足，本文提出的特征学习新方法可以从原始单词特征表示中学习到有益于分类的新特征表示；在大量广泛使用的文本数据集上的实验结果表明，相较于现有改进模型和其他经典的机器学习文本分类模型，RFNB模型取得了较好的实验效果.

1 相关工作

在众多朴素贝叶斯文本分类模型中，首先被提出的是多变量伯努利朴素贝叶斯文本分类模型(BNB).BNB假定文档由二进制特征向量表示，该向量表示哪些单词在文档中出现，哪些单词在文档中不出现.用d来表示1篇待分类的文档，其特征向量(w1,w2,…,wi,…,wm)表示构成文档的单词向量.BNB运用式(1)来分类文档d：

(1-Bi)(1-P(wi|c)))],

(1)

其中,C为文档所属类别c的集合，m是词库中不同单词的数目，即词库的大小，wi表示单词向量中的第i个单词，Bi表示第i个单词在文档d中是否出现，出现为1，不出现为0.先验概率P(c)和条件概率P(wi|c)分别运用式(2)(3)来估计：

(2)

(3)

其中，n是训练文档的数目，l表示文档的类别数目，cj是第j篇训练文档的类标记，wji表示第j篇训练文档中的第i个单词，其值为布尔类型，若第i个单词在第j篇文档中出现则wji=1，否则wji=0.δ(α,β)是一个二元函数，当α=β时δ(α,β)=1，否则δ(α,β)=0.

为了克服BNB忽略单词出现的频次信息这一不足，McCallum和Nigam[4]通过捕获文档中单词出现的频次信息，提出了一种多项式朴素贝叶斯文本分类模型.MNB运用式(4)来分类待分类文档d：

(4)

其中fi是单词wi在文档d中出现的频次，先验概率P(c)与BNB中计算方法一致，仍然运用式(2)来估计.条件概率P(wi|c)则运用式(5)来估计：

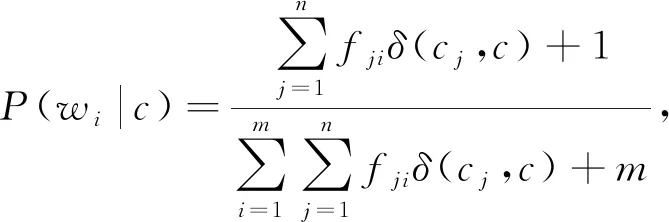
(5)

其中fji是单词wi在第j篇文档中出现的频次.

MNB较BNB具有更加广泛的应用，许多研究工作都以MNB为基准进行改进，但是MNB要求的属性条件独立假设在现实应用中往往很难得到满足.为了削弱它要求的属性条件独立假设，学者们提出了许多改进方法，蒋良孝和李超群[16]对这些改进方法做了详细总结，概括起来主要包括5类：结构扩展、实例选择、实例加权、特征选择、特征加权.

1.1 结构扩展

结构扩展方法通过在存在相互依存关系的特征之间添加有向边，由此来学习结构扩展的MNB模型.给定1篇待分类的文档d，结构扩展的MNB运用式(6)来分类文档d：

(6)

其中Swi表示贝叶斯网络中wi的父特征集.先验概率P(c)仍运用式(2)来估计，但条件概率P(wi|Swi,c)在估计时要首先通过结构学习确定每个特征的父特征集，这类似于学习一个最优的贝叶斯网络，被证明是一个NP-hard问题.

为了构建一种不需要进行结构学习但仍然可以在某种程度上考虑到特征之间依存关系的贝叶斯网络模型，Jiang等人[5]提出了一种结构扩展的MNB模型(structure extended multinomial naive Bayes,SEMNB).SEMNB提供了一种简单有效的学习方法，通过加权平均所有的一依赖多项式估计来削弱MNB模型要求的属性条件独立假设.SEMNB模型无需复杂的结构学习过程，保持了MNB模型的结构简单性.

1.2 实例选择

实例选择方法首先利用局部学习的思想从整个训练文档集中选择部分实例来组建待分类文档的邻域，然后在组建的邻域上构建MNB.给定1篇待分类的文档d，实例选择的MNB仍然运用式(4)来分类文档d，但先验概率P(c)和条件概率P(wi|c)分别运用式(7)(8)来估计：

(7)

(8)

其中k表示文档d的邻域中训练文档的数目.

为了组建待分类文档d的邻域，Jiang等人[6]提出了局部加权MNB模型(locally weighted multi-nomial naive Bayes,LWMNB).LWMNB采用K近邻算法来搜索待分类文档d的邻域，是一种典型的消极学习的模型.此外，Wang等人[7]受NBTree的启发，利用决策树算法来搜索待分类文档d的邻域，然后在决策树的叶子节点上构建MNB模型，从而提出了多项式朴素贝叶斯树模型(multinomial naive Bayes tree,MNBTree).大量实验表明，MNBTree具有良好的改进效果.

1.3 实例加权

实例加权方法首先为不同的训练文档学习不同的权值，然后在加权之后的训练文档集上构建MNB.给定1篇待分类的文档d，实例加权的MNB仍然运用式(4)来分类文档d，但先验概率P(c)和条件概率P(wi|c)分别运用式(9)(10)来估计：

(9)

(10)

其中Wj表示第j篇训练文档的权值.

为了学习得到不同训练文档的权值，Jiang等人[8]提出一种判别加权的MNB模型(discriminatively weighted multinomial naive Bayes,DWMNB).DWMNB首先用原始训练文档集构建一个MNB模型，然后在每次迭代中，根据MNB估计的条件概率损失为不同的训练文档分配不同的权值.最后用学到的实例权值更新所有训练文档，并在更新得到的训练文档集上训练新的MNB模型作为最终学到的模型.

1.4 特征选择

特征选择方法首先利用数据归约的思想从整个特征空间选择出一个最佳特征子集，然后在选择的最佳特征子集上构建MNB.给定1篇待分类的文档d，特征选择的MNB运用式(11)来分类文档d：

(11)

其中q表示被选择的特征数目，先验概率P(c)仍然运用式(2)来估计，但条件概率P(wi|c)运用式(12)估计：

(12)

为了从整个特征空间选择出一个最佳的特征子集，学者们提出了许多特征选择方法.其中Yang和Pedersen[9]对文本分类的特征选择方法进行了比较研究，总结并评估了基于文档频率、信息增益、互信息、卡方统计量、单词强度这5种特征选择方法.他们的实验结果表明，在不损失分类精度的前提下，信息增益和卡方统计量的效果最好.不过在特征选择的过程中，基于信息增益的选择方法没有考虑属性值个数对结果的影响，对属性值较多的单词有所偏好.作为对信息增益的补充和改进，Zhang等人[10]提出了一种基于信息增益率做特征选择的MNB模型(gain ratio-based selective multinomial naive Bayes,GRSMNB)，广泛的实验研究表明GRSMNB取得了很好的分类效果.

1.5 特征加权

特征加权方法首先为不同的特征学习不同的权值，然后在加权之后的训练文档集上构建MNB.给定1篇待分类的文档d，特征加权的MNB运用式(13)来分类文档d：

(13)

其中Wi表示单词wi的权值，先验概率P(c)仍然运用式(2)来估计，但条件概率P(wi|c)运用式(14)估计：

(14)

为了学习特征权值，Jiang等人[11]率先提出了一种相关性深度特征加权的MNB模型(deep feature weighted multinomial naive Bayes,DFWMNB).之后，Zhang等人[12]提出了一种基于决策树做特征加权的MNB模型(decision tree-based feature weighted multinomial naive Bayes,DTWMNB).2020年Ruan等人[13]在深度特征加权的基础上引入类依赖的思想，有区别地为不同类别上的每个特征学习不同的权值，由此改进MNB模型.此外，Kim等人[14]基于信息增益、卡方统计量以及一种风险概率的扩展版本提出了3种特征加权方法.Li等人[15]提出了另一种基于卡方统计量的特征加权方法，通过在训练阶段准确测量特征和类别之间的正向依赖来计算特征的权值.

2 随机森林朴素贝叶斯

如第1节所述，已有许多方法被用于削弱朴素贝叶斯的属性条件独立假设.大量的实验研究表明，这些改进方法可以提升朴素贝叶斯文本分类模型的分类性能.然而现有改进方法都是基于原始的单词特征来构建朴素贝叶斯模型，属性条件独立假设使得朴素贝叶斯模型假定单词之间完全独立，因此忽略了多个单词组合在一起时对分类的影响.由于实际情景中单词组合携带的语义信息往往比单个单词更加充分，基于这一问题，本文尝试用特征学习的方法来改进朴素贝叶斯文本分类模型，为此我们提出了一种双层贝叶斯模型：随机森林朴素贝叶斯(RFNB).模型的具体结构如图1所示，图1中document表示1篇文档，termm表示第m个单词在document中的出现次数，v1表示由所有单词特征在document中的出现次数构成的特征向量，特征向量中矩形的密集程度表示了特征的维度.第1层由随机森林构成，随机森林中的第T个基学习器用RandomTreeT表示，每个基学习器为1棵随机决策树.第1层利用随机森林从特征向量v1中捕获T维单词组合的高层特征，构成特征向量v2.由于v2的维度等于随机森林中基学习器的个数T，而T往往远小于单词维度m，因此特征向量v2的维度远远低于原始的特征向量v1的维度.第2层由BNB构成，由于BNB接受二进制特征，所以将特征向量v2进行一位有效编码(one-hot encoding)后转化为二进制特征向量v3.特征向量v3的维度为T×l，是特征向量v2的维度的l倍.最后在v3上构建BNB模型，并由BNB预测待测文档的类别class.

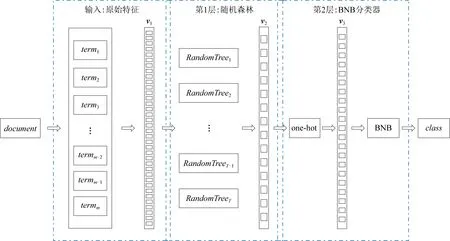
Fig.1 Structure framework of RFNB图1 RFNB的结构框架

可见，怎样从原始的单词特征中学习到单词组合的高层特征，以及怎样利用新特征构建高分类性能的朴素贝叶斯分类模型，是学习RFNB要解决的2个核心问题.下面的2.1节和2.2节将详细讨论如何解决这2个问题.

2.1 第1层：用随机森林学习新的特征表示

原始文本数据由原始的单词特征构成，特征值为单词在文档中的出现频率，单词空间的高维性导致了文本数据集的高维稀疏的特点.朴素贝叶斯的属性条件独立假设要求在给定类标记的前提下各特征之间完全相互独立，因而难以捕获多个单词组合的高层特征.RFNB第1层的任务就是从高维稀疏的单词特征中捕获单词组合的高层特征.

随机森林[17]作为Bagging的扩展变体，采用随机决策树作为其基学习器.Bagging有效防止在集成学习的过程中陷入过拟合，同时保证了随机森林各基学习器之间具有较高的独立性，随机决策树增加了训练基学习器时的随机性，进一步保证了基学习器之间的独立多样性.使用文本数据集训练随机森林，图2所示的树形结构表示1棵训练好的随机决策树，其中圆形节点表示分裂节点，三角形表示叶子节点，ti表示单词空间中的第i个单词特征，特征值为第i个单词在文档中的出现次数，用在分裂节点中表示使用该单词作为所在分裂节点的划分单词特征，numi表示第i个单词特征的最佳划分值.假定1篇文档经过这棵随机决策树的路径如阴影标记所示，最后落入一个叶子节点，并根据叶子节点的分类信息给出最终预测类别下标为1.

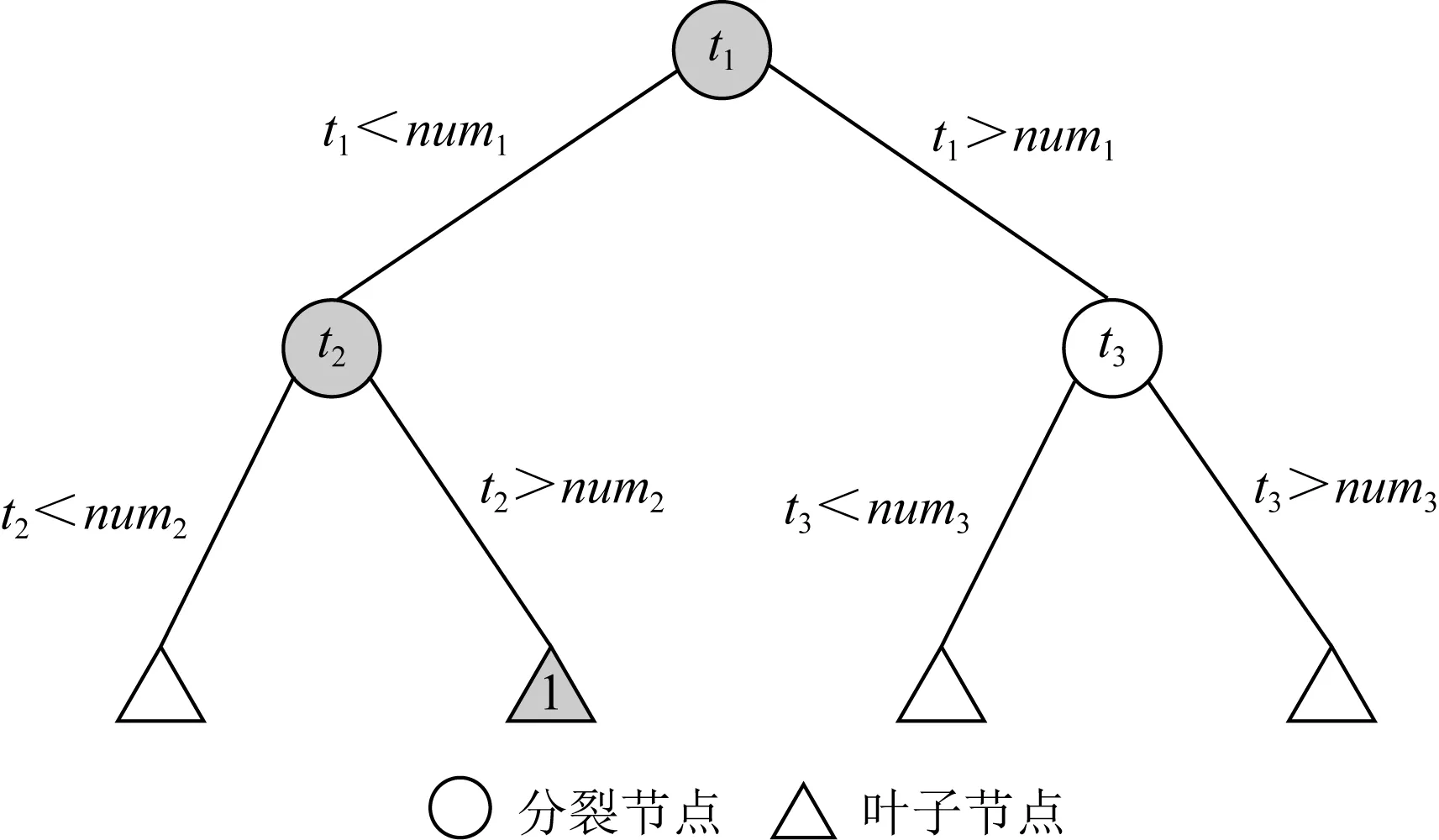
Fig.2 Structure diagram of random decision tree图2 随机决策树结构图

由于预测类别下标1的得出同时参考了单词t1和单词t2的频率信息，这表示在这棵树中当文档的单词t1的频率值小于num1且单词t2的频率值大于num2时，2个单词在这组具体特征值下的高层特征就可以用类别下标1来表示.类似上述情形，文档从输入随机决策树根结点到落入一个叶子节点的过程中，经过了一系列的中间节点，每个中间节点按照各自节点划分单词的特征值将文档送入对应的孩子节点，因此随机决策树的每个叶子节点上的类别下标输出都对应1组单词特征在不同的单词频率下的高层特征.因此1篇文档被随机森林中的每个基学习器分类的过程可以看作提取不同单词组合的高层特征的过程，且随机森林的Bagging和随机决策树的长树规则，保证我们学习这些不同的单词组合的高层特征更加容易.因此我们在第1层选择随机森林来进行特征学习，具体的算法步骤如下.

当给定文档集中文档的数目为n，随机森林中基学习器的数目为T时，针对给定文档集，采用装袋方式处理：先从文档集中随机选择1篇文档作为采样文档放入采样集，再把该采样文档放回初始的文档集，使得下次采样时该文档仍有机会被选中；经过n次采样，得到包含n篇采样文档的采样集；将采样过程重复T次，得到T个分别含有n篇采样文档的采样集.采样集之间相互独立，分别针对每个采样集构建随机森林中的一个基学习器.为了保证基学习器之间的独立性，文档数目n应远大于基学习器数目T.

本文所构建的随机森林中的基学习器是1棵随机决策树，在随机决策树的长树阶段，每次从给定的分裂节点中随机选取出kw个单词构成候选分裂特征集合A.从集合A中求出最佳分裂单词的最佳分割点，进行分割.kw的取值影响基学习器的分类性能和基学习器之间的差异性，经过实验分析，最终确定kw值：

(15)

其中m值为所有文档中不同单词的数目.

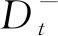
(16)

分类回归树(classification and regression tree,CART)[18]中采用基尼指数作为数值型特征的划分标准，分裂时仅将当前节点的数据集合分成2部分，分别进入左右子树，取得了良好的效果.同样地，RFNB采用基尼指数划分数值型单词特征.在本文中划分前后基尼指数的差值用基尼增益表示，单词w划分文档集D的最佳基尼增益值为

(17)

其中|D|为文档集D中的文档数目.

假定文档集D中文档的类别数目为l，文档集D中第j类文档所占的比例为pj(j=1,2,…,l)，文档集D的基尼值Gini(D)为

(18)

根据以上方法，分别求出候选分裂特征集合A中每个单词的最佳基尼增益划分点，然后计算当前节点的最佳分裂单词w*为

(19)

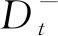
我们用构建好的随机森林对训练集中的每篇文档进行分类，然后用每篇文档在所有随机决策树上的预测类别下标构成一个类别下标向量，以此作为从原始文档中学到的新的特征表示.

综上所述，RFNB的第1层用随机森林将每篇原始文档从原始的单词特征表示转化为高层特征表示，并输入到RFNB的下一层.2.2节将详细介绍如何在新特征表示上构建朴素贝叶斯文本分类模型.

2.2 第2层：在新特征表示上构建BNB

通过RFNB第1层学习得到的新特征的特征值为预测类别的下标，虽然也是整型数值，但并不能作为单词在文档中出现的频次来使用，因此不能直接用于文本分类模型的学习，为了使新特征可以用于朴素贝叶斯文本分类模型的学习，本文对第1层学习得到的新特征做了一位有效编码(one-hot encoding).经过一位有效编码后的特征值变成了布尔类型，即只有0和1这2个值，刚好可以视作单词在文档中出现的频次(1表示单词在文档中出现，0表示单词在文档中未出现)，此时才可以用于朴素贝叶斯文本分类模型的学习.当文档集D中文档类别数目为l，随机森林中基学习器的数目为T时，经过一位有效编码产生的二进制特征表示的维度为T×l.

接下来的问题是，RFNB的第2层应该选择哪一种朴素贝叶斯文本分类模型.MNB相比于BNB的优势在于捕获了单词在文档中出现的频次信息.而新特征经过一位有效编码后的特征值是布尔类型，单词的频次只有0和1这2个值，因此MNB相比于BNB的优势消失.同时，MNB按照式(4)分类时，当单词的频次fi=0时，与之对应的累加项被彻底抛弃，这相当于完全忽略了未出现单词对文档分类的影响.不同于MNB，BNB依据式(1)分类不仅考虑了出现单词对文档分类的影响，还考虑了未出现单词对文档分类的影响.并且BNB忽略单词频次信息的不足刚好被一位有效编码得到的二进制特征表示所弥补，因此BNB被选为最终的朴素贝叶斯文本分类模型.

综上所述，RFNB分为2层，第1层采用随机森林做特征学习，然后将新特征输入第2层，经过一位有效编码后用于构建BNB.因此，RFNB的整个学习过程可以分为训练过程和分类过程，本文分别用算法1和算法2进行详细的描述.

算法1.RFNB-Training.

输入：训练文档集D；

输出：训练好的随机森林、P(c)、P(wi|c).

① 使用训练文档集D，根据2.1节描述的长树方法构建随机森林；

② 建立新的样本集合D′，D′初始为空；

③ 运用构建的随机森林分类D中的每篇训练文档x得到新的特征向量x′，并将新特征向量x′存入样本集合D′中；

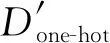
⑥ 返回训练好的随机森林、P(c)、P(wi|c).

算法2.RFNB-Classification.

输入：随机森林、P(c)、P(wi|c)、待分类文档d；

输出：待分类文档d的预测类别.

① 将待分类文档d输入随机森林，用基学习器预测的类别下标为d构建新特征向量d′；

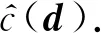
3 实验与结果

3.1 实验设置与实验数据

为了验证本文所提模型的有效性，本文从每一类现有改进方法中分别挑选了一种经典模型作为RFNB的比较对象，具体模型包括SEMNB[5]，MNBTree[7]，DWMNB[8]，GRSMNB[10]，DTWMNB[12].这些改进模型已经被证明具有很好的改进效果.除此之外我们还增加了支持向量机(support vector machine,SVM)[19]和随机森林(random forest,RF)[17]两种经典的文本分类模型作为比较对象.下面是所有这些比较对象的全称和缩写.

BNB：伯努利朴素贝叶斯[3]；

MNB：多项式朴素贝叶斯[4]；

SEMNB：结构扩展的MNB[5]；

MNBTree：多项式朴素贝叶斯树[7]；

DWMNB：判别加权的MNB[8]；

GRSMNB：信息增益率特征选择的MNB[10]；

DTWMNB：基于决策树特征加权的MNB[12]；

SVM：支持向量机[19]；

RF：随机森林[17].

我们在国际数据挖掘实验平台WEKA[20]上实现本文提出的RFNB，并设置随机森林中基学习器的数目T=200.实验数据为WEKA平台发布的15个广泛使用的标准文本数据集，代表了不同的文本分类场景和特征，具体信息如表1所示：

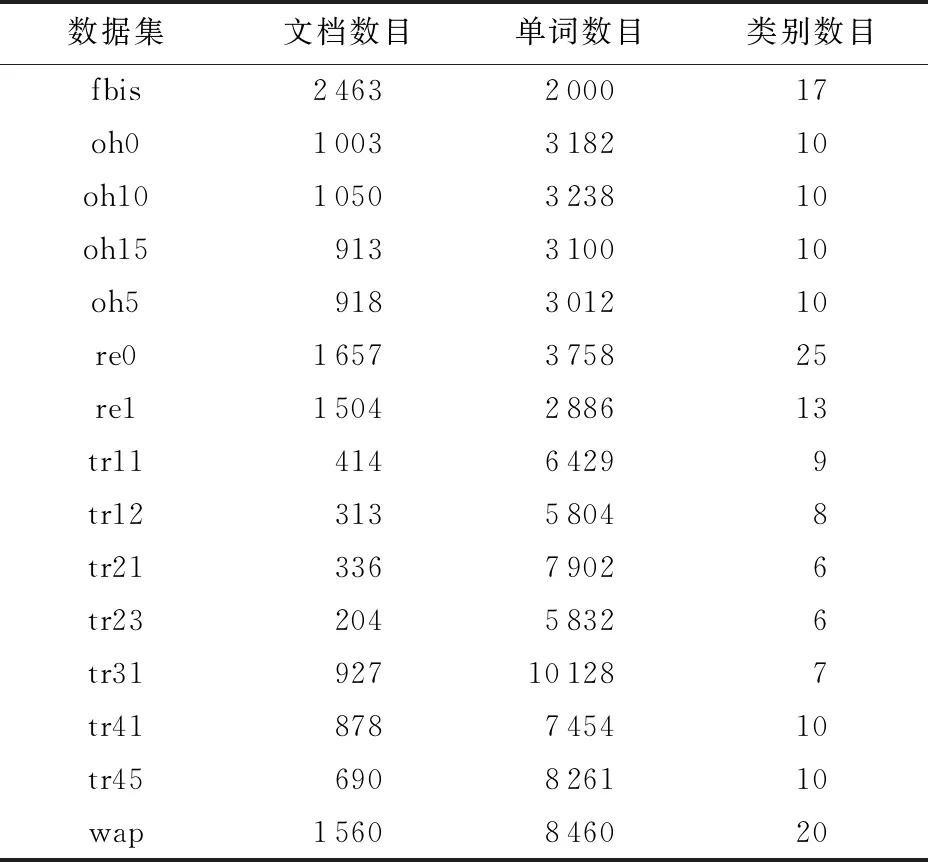
Table 1 The Detailed Description of 15 Datasets表 1 15个数据集的详细描述

3.2 实验评价指标

本文采用2种评价指标衡量算法的分类性能，分别是分类精度(classification accuracy)和加权平均F1值(weighted average ofF1,Fwa).分类精度是指算法分类正确样本占总样本的比例，是最常用的评价指标.Fwa用于衡量模型在多类问题中针对不同类别分类性能的整体表现，其具体计算为

(20)

其中，countj表示第j类文档样本个数，Fj表示当用第j类样本作为正类样本、其余样本作为负类样本时的F1值，Fj计算为

(21)

其中pj和rj分别表示对应情景下的精确率和召回率.

3.3 实验结果与分析

表2展示了本文提出的RFNB及其比较对象在每个数据集上通过10次10折交叉验证获得的平均分类精度，表3展示了实验获得各个算法的Fwa.表2和表3中每行加粗的数字表示在该数据集上获得的最高的分类精度或Fwa.作为各模型相对性能的总体指标，本文将每个模型在15个数据集上的平均分类精度和平均Fwa汇总在表格底部.

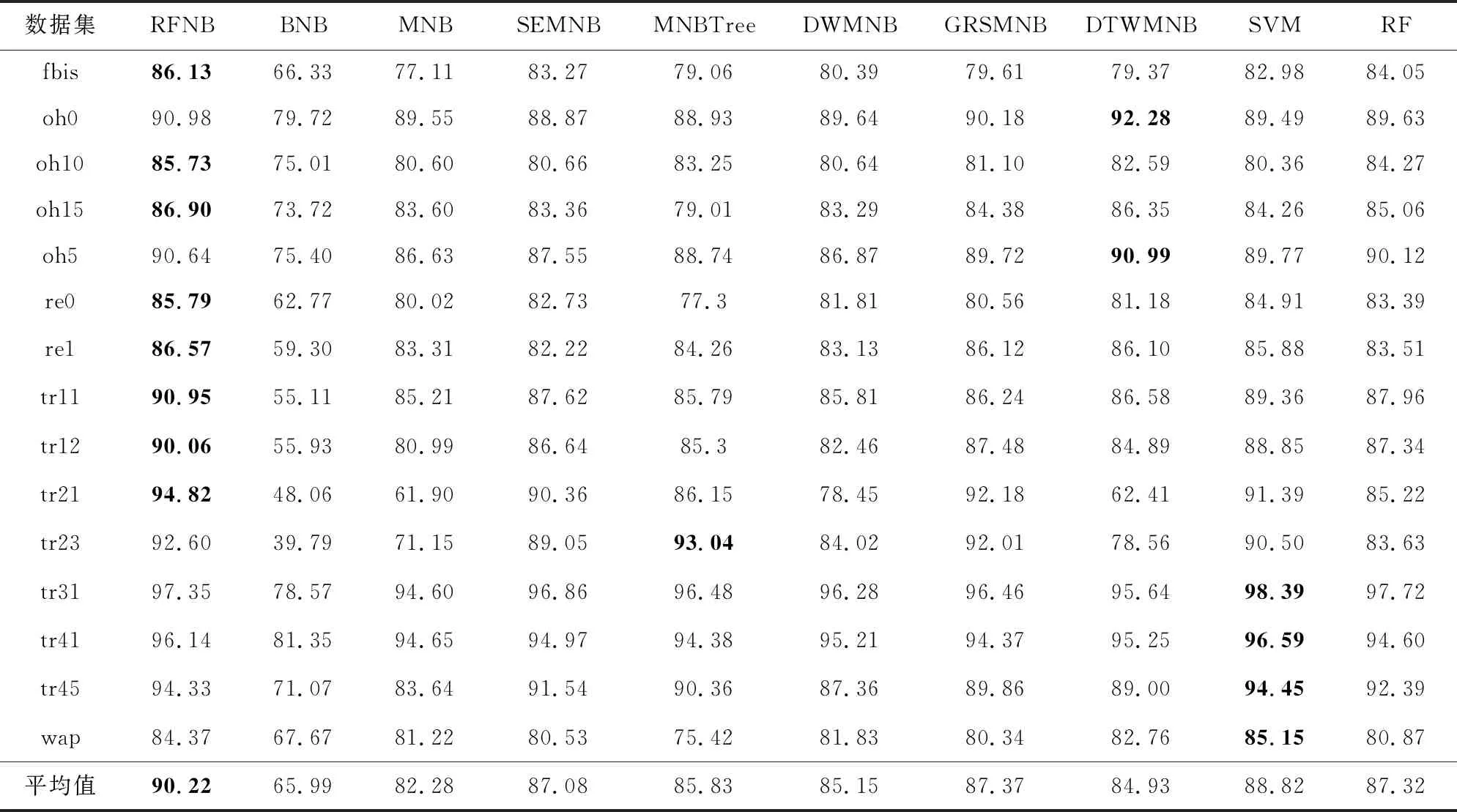
Table 2 Classification Accuracy Comparison for RFNB Versus Its Competitors表2 RFNB与其比较对象的分类精度比较结果 %

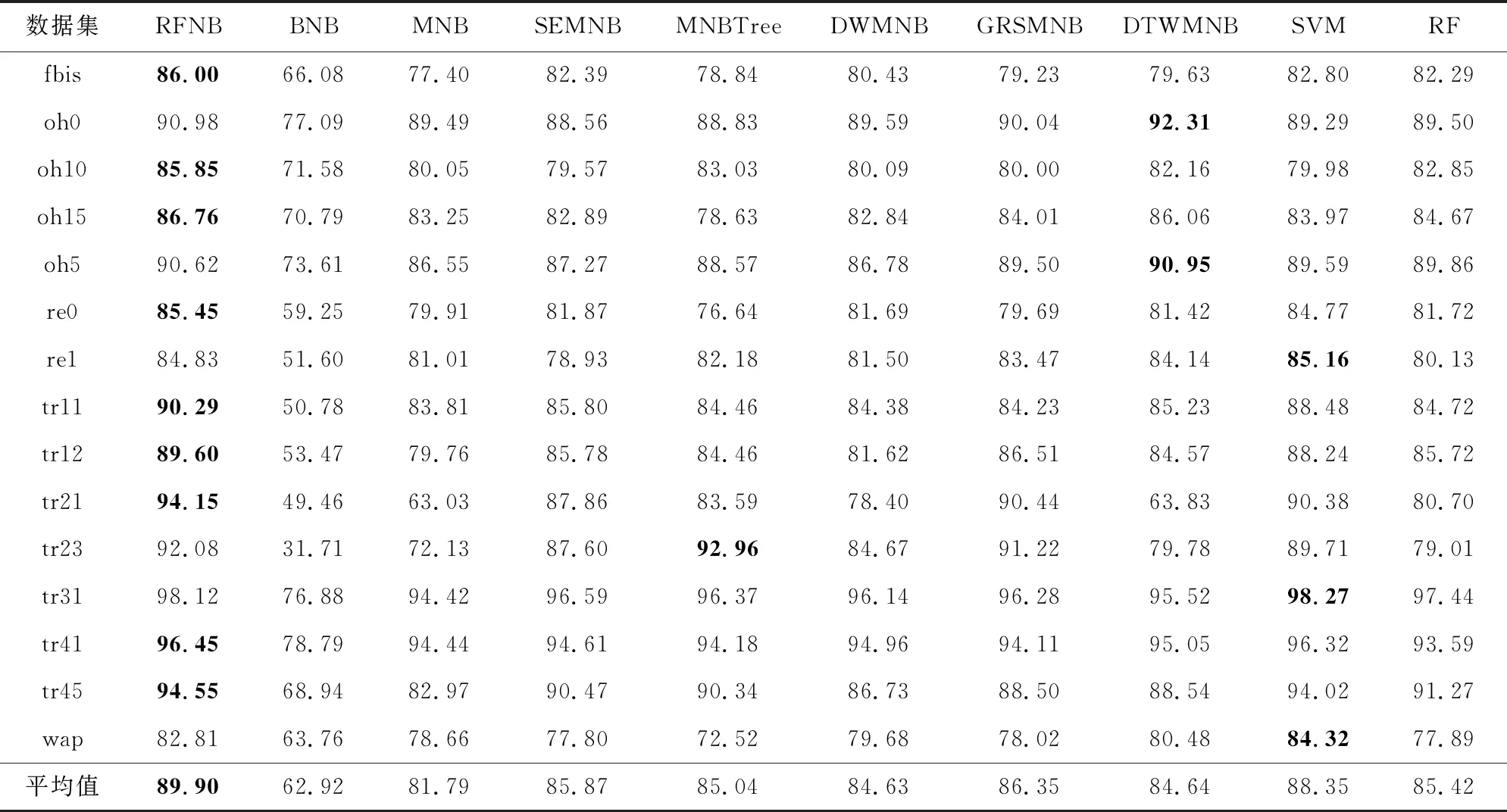
Table 3 Fwa Comparison for RFNB Versus Its Competitors表3 RFNB与其比较对象的Fwa比较结果 %

基于表2和表3，我们利用KEEL(knowledge extraction based on evolutionary learning)数据挖掘软件[21]进行了系统的威尔克森符号秩检验[22]，以进一步比较每一对模型之间的性能差异.威尔克森符号秩检验计算所得秩和如表4和表5所示.根据威尔克森符号秩检验的临界值表，显著性水平为α=0.05和α=0.1时，如果正差秩和与负差秩和中较小的一个小于或者等于25和30，则认为算法显著不同.由此得到详细的统计比较结果如表6和表7所示.

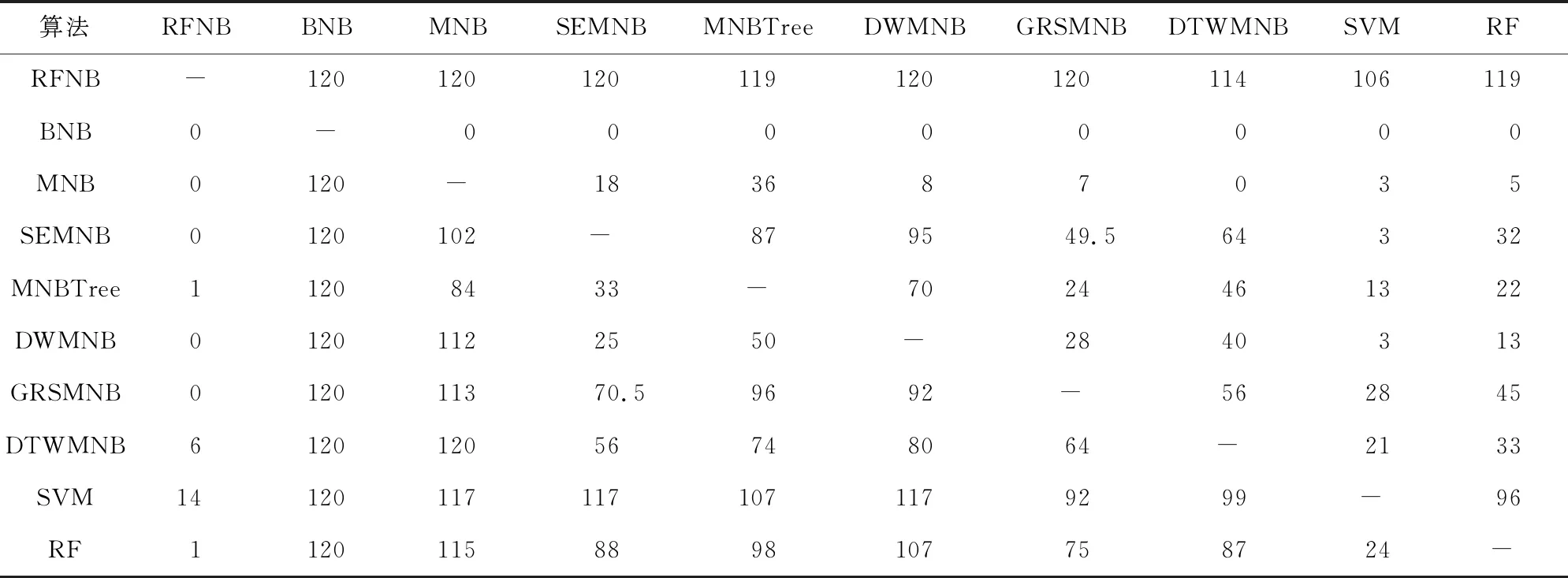
Table 4 Ranks of Classification Accuracy Computed by the Wilcoxon Test表4 分类精度的威尔克森测试的秩和值

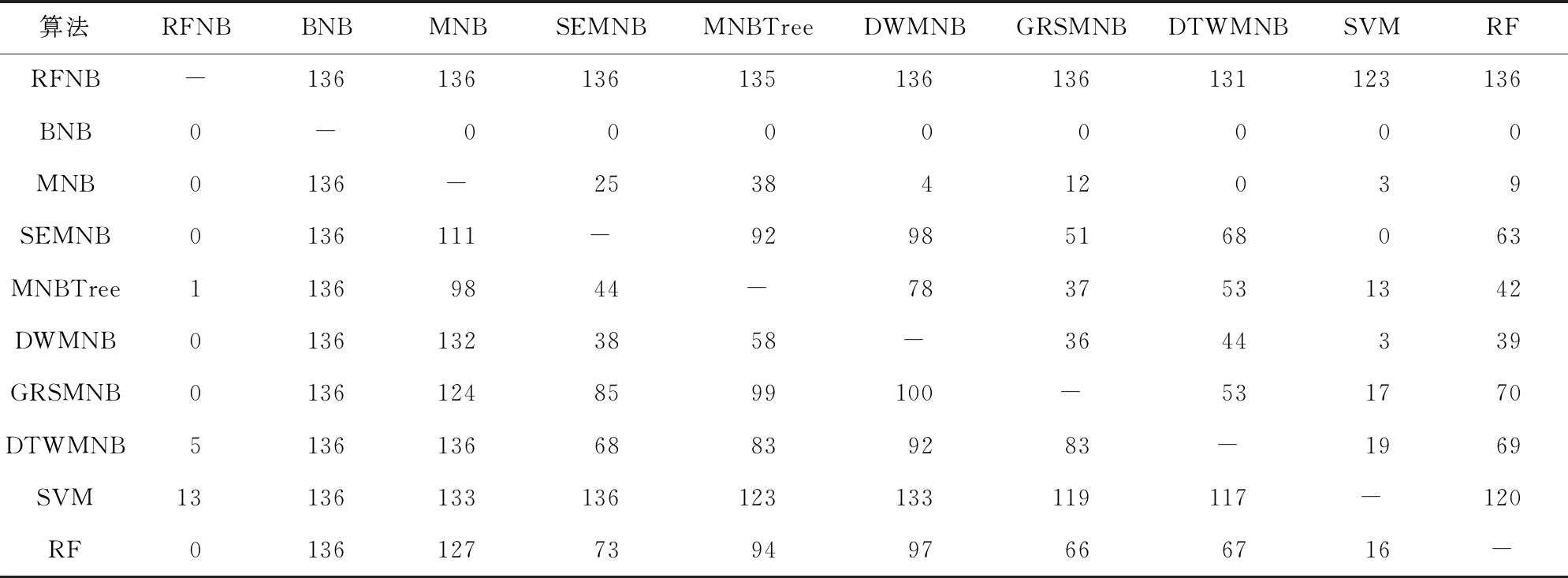
Table 5 Ranks of Fwa Computed by the Wilcoxon Test表5 Fwa的威尔克森测试的秩和值

Table 6 Classification Accuracy Comparison Results of the Wilcoxon Tests表6 分类精度的威尔克森测试的比较结果

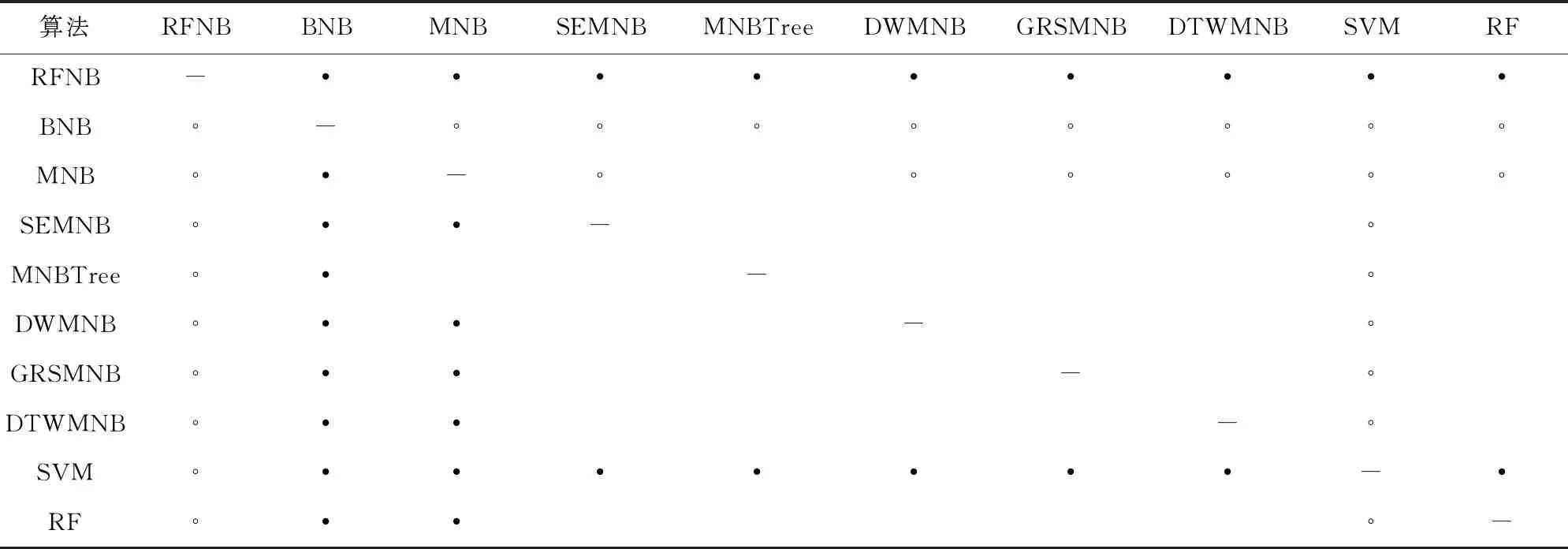
Table 7 Fwa Comparison Results of the Wilcoxon Tests表7 Fwa的威尔克森测试的比较结果

从表2～7可以看出：

1)直接在原始的文本数据上构建BNB，分类精度和Fwa都是最低的，在15个数据集上的平均分类精度仅仅只有65.99%，平均Fwa为62.92%.

2)相比于BNB，MNB因为捕获了单词在文档中出现的频次信息而获得了更好的分类性能，在15个数据集上的平均分类精度快速提升到82.28%，平均Fwa为81.79%.

3)相比于MNB，目前已有的5种改进模型SEMNB，MNBTree，DWMNB，GRSMNB，DTWMNB在15个数据集上的平均分类精度都有较大幅度的上升，分别上升到87.08%，85.83%，85.15%，87.37%，84.93%；平均Fwa也有较大提升，上升到85.87%，85.04%，84.63%，86.35%，84.64%.

4)本文提出的RFNB在15个数据集上的平均分类精度达到了90.22%，不仅比已有的5种改进模型都高，还高于经典的支持向量机(88.82%)和随机森林(87.32%)；平均Fwa达到了89.90%，同样高于上述文本分类模型.这说明本文提出的特征学习方法是非常有效的，新的特征表示更加有利于朴素贝叶斯文本分类模型做分类，最终学习得到的BNB模型分类性能达到了最佳.

5)在原始的文本数据集上直接构建BNB，其分类性能欠佳，甚至比最简单的MNB还要低大约17个百分点，但在本文得到的新特征表示上构建BNB，其分类精度竟然反超MNB大概8个百分点.这表明本文提出的RFNB，不仅可以从原始的单词特征中学习到由多个单词组合的高层特征，还可以弥补BNB因忽略单词频次信息造成的模型缺陷.

6)从表4～7所示的威尔克森统计测试比较结果来看，本文提出的RFNB显著优于所有的比较对象，包括BNB，MNB，SEMNB，MNBTree，DWMNB，GRSMNB，DTWMNB，SVM，RF.这充分证明了本文所提模型的有效性.

4 总结与展望

朴素贝叶斯文本分类模型的属性条件独立假设使得模型在面对文本数据时，只考虑了单个单词特征的语义信息而忽略了不同单词组合下的高层信息.目前所有削弱其属性条件独立假设的改进方法都是基于原始的单词特征来构建文本分类模型，这在一定程度上限制了改进方法的效果.不同于现有的改进方法，本文提出用特征学习的方法来改进朴素贝叶斯文本分类模型，提出了一种双层贝叶斯模型：随机森林朴素贝叶斯(RFNB).RFNB在第1层采用随机森林从原始的单词特征中学习单词组合的高层特征，然后将学到的新特征输入第2层，经过一位有效编码后用于构建伯努利朴素贝叶斯模型.在大量广泛使用的文本数据集上的实验结果表明，本文提出的RFNB模型明显优于现有的最先进的朴素贝叶斯文本分类模型和其他经典的文本分类模型.

在目前的实验中，随机森林中基学习器的数目被设置为固定值200，固定的参数设置不利于模型在不同维度的数据集上应用，将来的研究可以尝试设计一种随数据维度自适应的参数设置方法，如设置随机森林中基学习器的数目为数据维度的开方，以此进一步增强模型的泛化能力.此外，目前的版本中随机森林采用了固定的长树方法，这在一定程度上限制了学习高层特征时的多样性.将来的另一个研究方向可以尝试用不同的方法长树，以进一步提高基学习器的多样性，持续攀升模型的分类性能、拓展其应用场景.