一种基于增强图卷积神经网络的协同推荐模型

王 磊 熊于宁 李云鹏 刘媛媛

(西南财经大学经济信息工程学院 成都 610074)

协同过滤(collaborative filtering,CF)是推荐系统中的主要方法之一[1].根据是否采用了机器学习模型，它可以分为：基于内存的协同过滤[2-3]和基于模型的协同过滤[4-9].相比于前者存在的依赖于相似度函数、内存占用度高、难以发现实体之间的非线性和隐含联系等不足，基于模型的方法利用矩阵隐空间分解[4-5]、Markov链[6]、深度神经网络[7-8]等模型学习实体的嵌入表示，能够从实体交互操作及辅助信息中更有效地捕获实体间的复杂联系，是目前研究最广泛的推荐方法.

近几年，图卷积神经网络(graph convolutional neural network,GCN)的研究逐渐兴起[9-14]，由于具有在图结构上学习嵌入表示的强大能力，它成为当前推荐系统中最热门的研究方法[10-11,15-18].GCN利用谱图理论定义了图卷积操作，在拓扑图上传播和聚合邻居节点的消息，具有同时利用实体特征和图结构特征学习实体嵌入表示的优势.实质上，它是将传统卷积神经网络(convolutional neural network,CNN)[17]优良的特征学习和表示能力扩展到非规则的图数据上.

推荐场景中的实体及其交互关系可以很自然地用拓扑图表示，因而非常适于采用GCN模型实现基于图的推荐任务.近3年来，一些基于图卷积神经网络的推荐模型相继被提出.例如，Berg等人[10]使用GCN作为编码器在图自编码框架下实现了GCMC(graph convolutional matrix completion)推荐模型，它利用单个图卷积层在“用户-项目”二分图上聚合1阶邻居的协同信号，实现了端到端的评分预测.Wang等人[15]提出了一种NGCF(neural graph collaborative filtering)模型，它利用GCN的消息传递机制堆叠多个图卷积层，实现了二分图上高阶邻居的协同信号隐式传递，最后合并所有层的节点嵌入进行推荐，一定程度弥补了GCMC模型只能利用1阶协同信号的弱点.此外，一些学者从提升图卷积操作效率[16-17]、利用注意力机制[19-20]、引入辅助信息[21]、提高扩展性[11,22]、克服冷启动[23]等方面改进了基于GCN的推荐模型.这些研究均表明：得益于强大的特征表示学习能力，基于GCN的推荐模型能够更好地在实体交互图上捕获隐含、非线性的协同信号，通常获得了比传统协同推荐模型更优的准确率.

尽管图卷积神经网络已被公认在推荐任务中具有显著优势，但已提出的基于GCN的推荐模型通常忽视了2个方面的问题，尚需进一步完善.

1)大多数模型的图卷积层没有充分利用高阶邻居的协同信号.例如，GCMC只利用了1阶邻居的信号更新节点嵌入.而文献[24]的研究表明高阶邻居的协同信号同样对学习节点嵌入非常重要.此后的多个模型在GCN框架下堆叠多个图卷积层隐含地传递高阶协同信号[15-16,18,23]，但在他们的图卷积层内部仍然只用1阶邻居更新节点嵌入.该方式不仅很难控制聚合高阶信号时的强度，而且容易受到噪声的影响(详见1.3节的分析).2019年提出的GraphRec模型直接利用社交关系聚合了好友的协同信号[20]，但该方法并没有利用项目的高阶信号且需要额外的辅助信息.

2)现有模型的图卷积层在传播和聚合协同信号时很少重视用户的不同观点对推荐结果的影响.在推荐场景中，评分代表了用户的观点.例如，若用户对项目v1和v2分别给予的评分为2和5，则显然他对v2表达了更“喜欢”的观点，或者该项目更符合用户的偏好.然而，现有的大多数模型在聚合1阶协同信号时忽略了用户观点的差异[15-19,23].我们注意到，GCMC和文献[25]提出的模型试图在不同评分等级上分别聚合协同信号，但是他们的方法在合并多个等级的信号时仍然没有考虑用户观点的差别.

针对上述不足，本文以推荐系统中的评分预测任务为对象，研究利用2阶邻居的协同信号和用户观点来提升图卷积神经网络在学习节点嵌入时的准确性，进而提出一种增强的基于图卷积神经网络的协同过滤推荐模型——EGCN-CF(enhanced graph convolutional neural network based collaborative filtering recommendation model).

本文的主要贡献有3个方面：

1)提出一种直接从邻接矩阵计算2阶协同信号及其强度的方法，用于更新图卷积层的节点嵌入；

2)给出一种简便方法将用户观点融合入1阶协同信号聚合过程，以便利用用户偏好更准确地学习节点的嵌入表示；

3)结合1)2)方法，提出了一种增强的基于图卷积神经网络的协同推荐模型，并在多个推荐数据集上验证了其性能优势.

1 利用图卷积神经网络实现协同推荐

1.1 推荐系统中的评分预测问题的定义

在推荐场景中，假设已知稀疏的评分矩阵R∈m×n，它的少量非0元素ru,v∈{1,2，…,T}代表用户u对项目v的评分结果，共有T个等级；矩阵Xu∈m×du和Xv∈n×dv分别表示用户和项目的实体特征，其中，m和n分别是用户集和项目集的规模，du和dv分别是用户特征向量和项目特征向量的维度.评分预测的目标是：建立预测模型对大量尚未评分的项目给予准确地评分，进而实现项目推荐.

1.2 基于GCN的通用推荐模型

基于图卷积神经网络的推荐模型利用消息传递的思想在二分图上传播和聚合协同信号，学习节点的嵌入表示并用于推荐预测[10,15-16,18,26].它们的模型结构通常由3个部分构成：输入层、图卷积层和预测层.

e0=Enc(x,Θin)，

(1)

2)图卷积层.又称为“嵌入传播层”，它利用二分图的结构特征在图上传播和聚合邻居节点的协同信号，实现节点的嵌入更新.其主要操作包括：协同信号构造和节点嵌入更新.

以用户u对项目v的一次评分为例，该操作反映了用户对项目的一定程度的偏好.因此，可以将此次操作传播的1阶协同信号构造为

su←v=f(eu,ev,pu,v,Θf)，

(2)

嵌入更新操作在二分图上汇集所有1阶邻居的协同信号，用于更新用户u的嵌入表示：

(3)

其中，聚合函数g(·)可以采用均值、最大池化、LSTM网络等方式实现[13,18].

类似地，当项目v获得用户u的评分，表明项目的品质与用户偏好一定程度的相符.因此，可以利用用户的协同信号对项目实体的嵌入进行更新，即

sv←u=f(ev,eu,pu,v,Θf)，

(4)

(5)

这样，图卷积层利用1阶协同信号在二分图上实现了实体节点的嵌入表示的一次更新.

(6)

其中，预测函数h(·)通常采用双线性解码函数[10,25]或多层感知机网络[5,20]实现；Θh代表其参数集合.

1.3 问题分析

一方面，如1.2节所述，图卷积层采用的协同信号聚合式(3)(5)中，只使用了来自直接交互的1阶邻居和自身的协同信号，忽略了卷积层内的高阶信号.然而，根据协同过滤的基本思想[1]，用户行为或偏好还受到与之相似的其他用户的影响，他们在二分图上可视为相似的高阶邻居.因此，在图卷积层聚合高阶信号是非常有益的.近期，文献[27]也利用随机游走模型指出了高阶信号对于优化节点嵌入的价值.

一些基于GCN的推荐模型虽然通过堆叠多个图卷积层隐含地传播了高阶协同信号[15-16,18,23]，但这种方式难以控制高阶信号的强度，容易受到噪声的干扰.例如，假设在二分图上存在一条连通路径u0→v1→u2→v3→u4，其中，用户u4由于偶然原因评分了项目v3，尽管它与目标用户u0的偏好并不相似，但这次评分操作仍将导致u4的协同信号隐含地沿着堆叠的4个图卷积层逆向传递到u0，而不是被视为噪声信号受到抑制或消除.

另一方面，在图卷积层的聚合式(3)(5)中，所有的1阶邻居信号被同等对待，没有考虑用户观点(即评分值)的差别.显然，高评分项目的品味比低评分项目更能够反映用户的偏好[20,28]，应该在信号聚合操作中起到更大的作用.

2 提出的EGCN-CF协同推荐模型

本节将针对基于GCN的推荐模型存在的如1.3节所述的缺陷，提出一种端到端的EGCN-CF模型.它通过在图卷积层内引入2阶协同信号和用户观点，更有效地利用协同信号学习节点的嵌入表示，最后利用多层的感知机网络(multi-layer perceptron,MLP)实现对未知评分的预测.其基本结构如图1所示，包括输入层、增强的图卷积层和预测层3个部分.

2.1 输入层

EGCN-CF模型的输入层负责对用户或项目的实体特征进行编码，生成的低维嵌入向量作为图卷积层的输入.它采用的编码函数为

(7)

值得注意的是，式(7)采用了直接对用户或项目的原始实体特征进行编码的方法，获得它们的初始嵌入向量.相比于NGCF等模型采用的基于节点序号的独热编码方法[15-16]，该方法可以将语义更丰富的实体特征或辅助信息编码后输入到图卷积层，更有利于准确地学习节点的嵌入表示；并且，由于只需要优化编码矩阵，使得模型的优化参数更少.实验部分将具体描述对实体特征进行编码的细节.

2.2 增强的图卷积层

同NGCF模型类似，本文模型通过堆叠L个图卷积层实现节点嵌入表示的逐层精化.但我们针对现有模型的图卷积层的缺陷，通过融合2阶协同信号和用户观点进行了增强.本节以第l∈{1,2，…,L}图卷积层为例介绍其主要操作.

2.2.1 构造的2阶协同信号

如1.3节的讨论，在图卷积层中聚合高阶协同信号有益于节点嵌入表示的学习.但是，本文模型只使用了所有高阶邻居中的2阶邻居的协同信号，主要原因有2点:1)根据Xu等人[27]的研究，连通路径上高阶邻居的协同信号的强度随着阶数增加而迅速衰减，并且噪声信号容易在路径上积累，实际上该论断也一定程度解释了许多基于GCN的模型只堆叠了3或4个图卷积层的原因[15-16]；2)2阶邻居是与目标用户(项目)有共同交互项目(用户)的同质实体，按照三元闭包理论的解释[29]，2阶邻居相对于更高阶邻居而言，它们与目标实体的偏好更为相似，并且，与目标实体共同的交互实体越多，相似度越高.此外，第3节的实验结果也验证了增加同质的4阶邻居的协同信号不能明显提高推荐模型的性能.

(8)

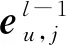
(9)

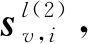
令El-1∈(m+n)×h是第l-1层所有嵌入向量组成的矩阵；Sl(2)∈(m+n)×h表示第l层所有节点汇集的2阶协同信号矩阵，其行向量由或构成.根据谱图理论知识[31]，可以整理出2阶协同信号矩阵Sl(2)的简洁形式：

(10)

(11)

2.2.2 带用户观点的1阶协同信号

用户对项目的评分不仅说明他们之间存在交互关系，更重要的是评分具体表达了用户的观点.例如，在电影推荐中，用5分、3分、1分表达了用户的“非常喜欢”“一般喜欢”“不喜欢”3种不同的观点.根据文献[28]的解释，获得了正向观点的高评分项目更能反映用户的真实偏好.因此，在汇聚1阶协同信号时融入用户观点，能够更准确地学习用户嵌入.

我们借鉴GCN的消息传递机制，给出一种带用户观点的1阶协同信号构造方法.它把汇聚到用户ui的1阶协同信号定义为

(12)

显然，高评分项目的观点系数取较大值，其传递的协同信号更多，反之亦然.因此，这种带观点的方式更合理地聚合了1阶协同信号.

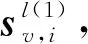
同样，我们根据谱图理论整理出带观点的1阶协同信号的简洁矩阵形式，即

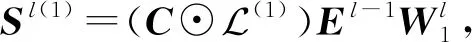
(13)

2.2.3 节点的嵌入更新

我们汇集1阶、2阶协同信号以及节点前一层的嵌入，对第l层的节点嵌入向量进行更新，如

(14)

此后，EGCN-CF模型可以堆叠L个图卷积层，按照式(14)实现嵌入表示的逐层精化，也即，依次获得E1,E2,…,EL.

2.3 非线性预测层

(15)

其中，W3∈2h×d′,W4∈d′×1是待学习的MLP权重矩阵；d′是MLP第1层(隐层)神经元的数量.

需要指出的是，相比于一些文献采用的线性预测模型[10,15-16,18]，本文采用非线性的MLP模型具有对节点嵌入向量之间复杂关系的更强的拟合能力，更适用于评分预测问题.

2.4 模型训练

EGCN-CF模型是一种端到端的推荐模型.为了训练其模型参数，我们给出一种基于均方误差的优化目标函数：

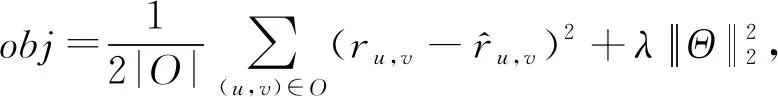
(16)

此外，在模型训练时还借鉴文献[15]采用的节点dropout技术防止过拟合，其dropout率为η.

最后，我们采用Adam梯度下降优化器对式(16)进行优化[32]，并采用小批量(minibatch)技术提高模型训练效率.

2.5 讨 论

在EGCN-CF模型的图卷积层中，显式地增加了对同质的2阶邻居的协同信号的聚合.从理论上讲，它可以聚合更高阶的协同信号.例如，在二分图上同时聚合2阶和4阶的同质协同信号时，只需简单地将式(11)替换为式(17)即可：

(17)

另外，在文献[20]的推荐模型中，将社交网络中好友的协同信号聚合到图卷积层.社交好友相当于二分图上具有高相似性的同质高阶邻居，聚合其协同信号显然有利于学习用户节点的嵌入表示.与之相比，本文模型通过矩阵运算对2阶邻居及其信号强度进行了合理的计算，无需额外的辅助信息.并且，当数据集中存在关于同质节点关系的辅助信息时，比如，社交关系矩阵Qu∈m×m，项目相似性矩阵Qv∈n×n，通过修改式(11)很容易把它们融入本文模型，如

(18)

其中，α是融合参数.

最后，EGCN-CF的3层结构与文献[15]的NGCF模型有相似之处，但它们在输入层、2阶协同信号利用、用户观点结合、预测层设计等方面具有显著差异.

3 实验与分析

为了验证提出的EGCN-CF推荐模型在评分预测任务上的性能，我们在5个通用的推荐数据集上进行了实验，并将它与主流的推荐模型进行性能对比.

3.1 数据集

表1概括了实验用数据集的情况.其中，Flixster和Douban直接使用文献[33]提供的预处理后的数据集；ML-100K，ML-1M，ML-10 M是来自于Movie-Lens网站的不同规模的电影推荐数据集(1)https://grouplens.org/datasets/movielens/.

在预处理阶段，我们在二分图上直接利用辅助信息和图结构特征对用户和项目的原始实体特征进行编码.对于Flixster和Douban数据集，实体特征由3个部分连接获得：节点度F1、评分特征F2、邻接关系特征F3.其中，评分特征F2统计了用户(或项目)给予(或获得)的不同等级评分的比例，邻接关系特征F3体现了同质节点之间的邻接关系，本文将其设置为用Node2vec模型[34]在用户或项目邻接矩阵上生成的256维向量.对于MovieLens数据集，项目的实体特征由节点度F1、评分特征F2、语义特征F3三部分组成.其中，语义特征F3采用文献[28]中的实验方法，对电影类别、名称、发行年编码获得，用户的实体特征由节点度F1、评分特征F2、人口统计特征F3、交互项目的平均语义特征F4四部分组成.其中，人口统计特征F3是由年龄、性别、职业编码的23维向量.表1最后2列给出了编码后的用户和项目的实体特征维度.

Table 1 Statistics of Experimental Datasets表1 实验数据集统计

3.2 实验设置

实验中，我们选取4种主流推荐模型作为对比算法，包括：NeuCF[5]，GCMC[10]，GraphRec[20],NGCF[15].其中，NeuCF是近几年提出的基于矩阵分解的协同推荐模型，它采用深度神经网络代替嵌入向量的内积运算，实验中我们采用式(16)替换其原优化目标，使之能够适用于评分预测任务.其他3种模型都是目前主流的基于GCN的协同过滤推荐模型，其中，对于GraphRec模型，我们采用用户的2阶邻居模拟其在MovieLens数据集上的社交关系；对于NGCF模型，我们也采用式(16)代替其原有的成对BPR(Bayesian personalized ranking)损失目标函数，以便进行评分预测.

我们用Tensorflow实现了本文的EGCN-CF模型，其主要参数配置为：节点嵌入维度h=64，图卷积层的数量L=3，正则系数λ通过交叉验证的方法在{0.01,0.05,0.1,0.5,1,5,10}范围内选取，MLP的隐层参数d′=16；训练时Adam优化器的学习速率设置为10-3，最大迭代次数为1 000次，每批训练数据规模设置为1 024，节点dropout概率η=0.3.对比算法的参数基本按照原文设置.

另外，将数据集按0.8，0.1，0.1的比例划分为训练集、验证集和测试集.在验证集上实现模型参数的选取，并采用均方根误差(root mean square error,RMSE)指标在测试集上评价各模型的预测误差.

3.3 对比实验

我们在各数据集上比较EGCN-CF模型与对比算法的性能，它们在测试集上预测时的均方根误差如表2所示.这里，除GCMC的结果来自于文献[10]外，其他结果都是3次重复实验的平均值.

Table 2 Comparison of Prediction Errors (RMSE)of Different Recommendation Models表2 比较不同推荐模型的预测误差(RMSE)

观察表2的实验结果，可以得出4个结论：

1)基于图卷积神经网络的4种推荐模型的预测误差明显优于基于矩阵分解的NeuCF模型.这说明受益于在拓扑图上融合了节点的实体特征和图结构特征，前者能够更加准确地学习节点的嵌入表示，从而获得更好的预测结果.

2)GCMC模型由于采用1个图卷积层，只能聚合1阶邻居的协同信号，对节点嵌入的学习能力不足，因而它在4种基于GCN的推荐模型中表现最差，特别是在非常稀疏的Flixster数据集上.

3)GraphRec和NGCF模型都利用了高阶协同信号，均取得了优于GCMC的预测结果.不同的是，GraphRec直接聚合社交好友的协同信号，他们相当于二分图中的相似的高阶邻居；NGCF则通过堆叠多个图卷积层隐式地传播和聚合高阶协同信号.这说明了聚合高阶协同信号有助于提高推荐模型的性能.

4)本文的EGCN-CF模型在绝大部分数据集上均取得了最低的预测误差，仅仅在Douban数据集上稍微高于GraphRec模型.并且，我们通过采用“A/B测试”进行显著性检验，发现本文的EGCN-CF模型的实验结果在大多数情况下以95%置信度显著优于其他模型(仅在3种情况下无明显优势，包括：在Douban,ML-1M数据集上与GraphRec比较、在ML-1M数据集上与NGCF比较).本文模型的优异性能可以归结于它在图卷积层中增加了对更高阶协同信号的利用和将用户观点引入信号聚合过程.与之相比，GraphRec只是从社交关系中直接获取了用户的高阶协同信号，并未考虑项目的高阶信号；NGCF模型并未在图卷积层内部显式地利用高阶协同信号，也未考虑用户观点的影响.

3.4 EGCN-CF模型的进一步分析

Table 3 Comparison of Prediction Errors (RMSE)of Different Variant Models表3 比较不同变体模型的预测误差(RMSE)

观察表3的实验结果，可以发现：

1)尽管EGCN-CF-a4模型增加了4阶协同信号，但其取得的预测误差与基本模型相当.这说明由于更高阶的协同信号强度较弱且可能带有噪声，无助于明显提高推荐模型的性能，这也是本文模型在图卷积层中只增加同质的2阶协同信号的原因.

2)去掉用户观点的EGCN-CF-do模型在各数据集的预测误差相比于基本模型均有一定程度的增大.这说明结合用户观点有利于提高推荐模型的性能.

3)去掉2阶协同信号的EGCN-CF-oo模型在各数据集上表现最差.例如，Flixster数据集上的误差相比基本模型增大了2.1%.这表明在图卷积层中增加2阶协同信号有利于提升评分预测的准确率.

4)采用线性预测层的EGCN-CF-1模型也取得了较低的预测误差，稍差于标准模型.这表明：一方面图卷积层已经能够学习获得准确的节点嵌入表示，即使利用简单的线性预测方法也能获得较好的准确率；另一方面，采用非线性的预测层能进一步提高模型的预测准确率.

3.5 图卷积层数量的影响

考虑到NGCF和EGCN-CF都堆叠了多个图卷积层，实现对节点嵌入的逐层精化.我们通过实验考察2种模型取不同数量的图卷积层时的预测误差情况.出于篇幅原因，我们只给出在Flixster和ML-100K数据集上的对比结果，如图2、图3所示:

Fig.2 Effect of graph convolutional layer numbers on Flixster图2 在Flixster数据集上图卷积层数量的影响

Fig.3 Effect of graph convolutional layer numbers on ML-100K图3 在ML-100K数据集上图卷积层数量的影响

分析图2，3中的结果，可以观察到：

1)2种模型的预测误差均明显受到图卷积层数量的影响，在2个数据集上呈现相似的变化趋势：预测误差先是随着层数增加而明显降低，但在3层以后，不再明显降低并出现小幅增加的现象.这说明堆叠过多的图卷积层容易产生过拟合问题.因此，本文模型的最大层数设置为3.

2)在各种情况下，本文模型的预测误差均明显优于NGCF.特别是当图卷积层的数量较少时，其优势更加明显.该现象得益于EGCN-CF采用的增强图卷积层的优势，它通过在层内聚合2阶协同信号和融入用户观点，更合理地聚合了协同信号，提高了节点嵌入学习的准确性，因而在图卷积层较少的情况下也能获得优异的预测准确率.

4 总 结

本文以推荐系统中的评分预测问题为对象，提出一种端到端的、基于增强图卷积神经网络的协同推荐模型.它通过增加2阶协同信号和融入用户观点，得到一种增强的图卷积层，并堆叠多个层次更合理地捕获二分图上的协同信号，提高对节点嵌入学习的准确性，最后利用非线性MLP网络实现评分预测.在多个推荐数据集上的实验结果表明，本文模型的预测准确率优于现有的推荐模型.

本文模型在运行时需要存储二分图的邻接矩阵，在超大规模图上可能遭遇存储瓶颈.在未来的研究工作中，我们将研究借鉴文献[11]的基于随机游走的节点采样技术，对本文模型进行改进，使其能够适应超大规模的推荐应用.