基于多特征融合的动力电池 RUL 预测

梁丹阳 程相 郗建国 李宗召 高建平

摘要：针对车载动力电池容量测试成本高及剩余使用寿命（remaining useful life，RUL）预测精度低的问题，提出一种基于多特征融合的动力电池 RUL 预测方法。首先对某款纯电动客车的动力电池历史运行数据分析，挖掘出能够代表动力电池性能衰减的特征参数;然后利用小波变换（wavelet transform，WT）去除采集过程中的干扰信号，并通过主成分分析法（principal component analysis，PCA）得到降维并去除冗余后的融合特征因子，利用融合特征因子构建基于遗传算法优化的支持向量回归（supportvector regression，SVR ）预测模型;最后通过在哈尔滨、合肥及郑州3个城市的历史运行数据进行验证。结果表明：该方法能够准确地预测出3个动力电池的容量，且去噪后的预测误差平均降低60%。

关键词：剩余使用寿命;融合特征因子;支持向量回归;小波变换;主成分分析

中图分类号： U469.72;U472;TM912文献标志码： A文章编号：1674–5124（2021）12–0149–08

RUL prediction of power battery based on multi-feature fusion

LIANG Danyang1，CHENG Xiang2，XI Jianguo1，LI Zongzhao1，GAO Jianping1

（1. School of Vehicle and Traffic Engineering， Henan University of Science and Technology， Luoyang 471003， China;2. Yutong Bus Co.， Ltd.， Zhengzhou 450016， China）

Abstract： Aiming at the high cost of vehicle power battery capacity test and the low accuracy of remaining useful life prediction， a prediction method of RUL of power battery based on multi feature fusion is proposed. Firstly，thehistoricaloperationdatasofthepowerbatteriesofaelectricbuswasanalyzed，andthe characteristic parameters which can represent the performance degradation of the power battery were mined. Then， the interference signal in the acquisition process was removed by wavelet transform， and the fusion featurefactorafterdimensionreductionandredundancyremovalwasobtainedbyprincipalcomponent analysis，and thesupport vector regression prediction model basedongeneticalgorithmoptimization was constructed by using fusion feature factors. Finally， through the historical operation data of Harbin， Hefei and Zhengzhou， the resultsshow that the proposed method can accurately predict the capacity of three power batteries， and the prediction accuracy after denoising is improved by more than 60%.

Keywords： remaining useful life; fusion feature factors; support vector regression; wavelet transform; principal component analysis

0引言

动力电池作为电动汽车的动力来源，其性能优劣影响电动汽车行驶过程中的动力性、经济性及安全可靠性[1]。

动力电池 RUL 预测目前主要有基于模型和基于数据驱动预测[2]。电池模型包括电化学模型和等效电路模型。电化学模型存在内部参数获取难度大，计算复杂的问题[3-5];等效电路模型利用等效电路元件模拟电池的外部工作特性，存在通用性差及参数辨识误差大的问题[6-7]。基于数据驱动的动力电池 RUL 预测，无需对其内部电化学反应及其失效机理过程进行深入研究学习，成为当前电池 RUL 预测的研究热点[8]。

目前多数基于數据驱动的电池 RUL 预测研究，通过电池实验，选取合适的健康因子进行电池的 RUL 研究，且大多研究利用电池的容量或阻抗作为健康因子进行电池的 RUL 研究[9-10]。比如王瀛洲[11]等采用 NASA 的卓越故障预测研究中心（prognosticscenter of excellence， PcoE）实验数据，提出了 ALO-SVR 算法进行锂电池的 RUL预测;陈万等[12]利用 NASA 的容量衰退数据，提出了随机扰动无迹粒子滤波算法。但是实验工况无法完全模拟实车行驶工况，实际应用中存在系统性差的不足;此外，容量、阻抗等数据的采集，需要昂贵、精密的专业设备进行测量，难以直接获取，时间长，成本高。已有部分文献，利用电池管理系统（battery management system，BMS）易监测的数据作为电池健康因子进行电池 RUL 预测。如文献[13]选择了电池端电压作为健康因子;文献[14]采用等压降时间间隔作为健康因子。上述研究虽然采用了BMS 易监测的特征因子，但未将提取影响电池性能退化的多个影响因素进行相关性分析及多特征融合，未充分包含电池的退化信息，且未考虑数据在采集过程中的噪声干扰。基于上述分析，本文提出一种基于多特征融合的动力电池RUL 预测方法，利用小波变换有效去除数据采集过程中的噪声，并利用主成分分析法将影响动力电池性能衰退的多个特征参数进行融合，既能够全面包含电池的衰退信息，又可以消除特征参数间的冗余信息。

1基于 WT-PCA-SVR 的动力电池 RUL 预测框架

本文的动力电池 RUL 预测框架如图1所示，主要分为以下几个部分：1）对动力电池运行的状态数据进行相关性分析，根据 Spearman 相关性系数，选取能够代表动力电池性能退化的特征参数。2）考虑到动力电池运行数据在采集过程中受到的噪声干扰，对提取的动力电池特征参数进行 WT 去噪，提高模型的学习准确性。3）针对动力电池特征参数间存在信息重叠及高维的问题，影响模型的准确性和复杂性，采用 PCA 对其进行降维、去除冗余的融合处理。4）利用融合特征因子构建基于遗传算法优化的支持向量回归模型对电池 RUL 进行预测。

2融合特征因子构建

2.1动力电池特征参数提取

动力电池性能衰退特征参数选取优劣直接影响预测模型的精度，考虑到动力电池的容量测量难度大，测试负载重等问题，基于影响动力电池老化的因素分析[15-17]。将各个充放电循环下的电池状态参数与容量进行相关性分析，选择 Spearman 相关性系数比较大的参数作为动力电池的特征参数。

2.2小波变换

考虑到采集动力电池状态数据的过程中存在噪声干扰，影响模型的学习准确性。对提取的动力电池特征参数，进行小波分解，依据特征参数正常信号与噪声信号的小波系数大小不同，设定小波系数阈值，剔除历史运行数据中的高频干扰信号，并进行小波重构，还原去噪后的特征参数，去噪前后数据长度不变。

实车采集的动力电池数据以离散形式存在，采用离散小波变换去除采集数据中的干扰信号。

离散小波：

式中：wj，k（t）——离散小波;

w ——小波函数;

t——时间变量;

a0——固定伸缩步长， a0>1;

b0——均匀采样基本间隔， b0>0;j， k e Z。

小波系数：

式中：ωw——小波系数;

x——含噪的动力电池特征参数。

2.2.1小波阈值设定1）固定式：

λ1=σ√2lnN （3）

式中：σ——特征参数噪声的标准差;

N——噪声数据个数。

2）自适应式：

其中Qa为小波系数的平方。

3）启发式：

式中：ω——小波系数;

f1——目标函数，表示数据起伏程度;

f2——对比函数。

2.2.2阈值函数

对小波去噪常用软阈值和硬阈值两种去噪方法。对于硬阈值去噪，在λ处不连续，小波重构会出现明显震荡;而软阈值去噪，虽在λ处连续，但小波系数存在固定偏差;上述方法虽然计算简单，但均有不足之处，影响特征参数重构精度。本文采用改进的阈值函数，可以明显提高其重构的精度。

改进的阈值函数：

式中：ωw′和ωw——修正前后的小波系数;

λ——设定阈值;

sgn（）——符号函数。

通过离散小波的逆变换进行小波重构，还原去噪后的动力电池特征参数xi，表达式如下：

2.3基于 PCA 的融合特征因子构建

针对动力电池的特征参数间存在信息重叠及高维问题，利用 PCA 对特征参数进行降维、去除冗余的融合处理，将累计贡献率超过90%的主成分作为动力电池性能衰退的融合特征因子。

主成分分析：

1）样本输入矩阵：

式中：m——样本个数;

s——特征参数个数。

2）标准化。为消除特征参数的不同量纲影响，

将特征参数值xij标准化：

式中：xij——标准化后的特征参数;

xj ，sj——第j个特征参数的样本均值及标准差。

3）系数矩阵 R=（rij）m×s

4）计算特征值λi及特征向量。5）特征值的贡献率ρi，累计贡献率ρ及主成分确定。

将累计贡献率超过90%的前 q 个主成分作为动力电池的融合特征因子。

3 GA-SVR 预测模型

3.1 SVR 模型

SVR 基于一个非线性映射把低维非线性问题通过核函数转换为高维空间的线性问题求解，从而对样本进行线性回归分析。样本训练集：S ={（x1 ，y1） ， （x2 ，y2） ， ··· ， （xn ，yn）}（ xi为融合特征因子，yi为目标变量）。线性回归函数：

式中：！——权重系數;

?（x）——非线性映射;

b——偏置值。

根据结构风险最小化准则，SVR 引入线性不敏感损失函数ε、松弛变量{ξi}1和{ξi*}1及惩罚因子G，求解参数！和b。

（ξi+ξi*）——训练误差;

式（16）引入拉格朗日乘子（αi， αi*），满足 Mercer 条件的核函数K（xi ·xj），得上式的对偶问题。

利用高斯径向基核函数，求解两个低维空间的特征向量在高维空间中对应的向量内积值。

其中σ为高斯径向基核函数宽度系数，影响低维到高维空间的映射特征及空间复杂度。

SVR 预测模型：

3.2 GA 算法优化

利用 GA 高效、并行的特点，对 SVR 的超参数 G、σ及ε进行全局寻优。GA 优化流程如图2所示。

4实验及结果分析

4.1评价指标

采用平均绝对百分比误差（ mean absolute percentage error，MAPE），均方根误差（root mean square error，RMSE）作为模型精度的评价函数。采用信噪比（SNR）和 RMSE 作为特征参数的降噪评价指标。

式中：f（xi）与yi——动力电池容量的预测值和真实值;

xi和xi（′）——去噪前后的特征参数;

N——特征参数个数。

4.2动力电池数据分析

采用某公司生产纯电动客车从2018年12月至2019年12月分别在哈尔滨、合肥及郑州三个城市的历史运行数据进行验证。整车参数如表1所示。首先对纯电动客车每日的历史运行数据进行分析，及充放电过程划分，每日进行一次充放电，将每天的充放电循环的容量均值作为该循环的实际容量，得到容量随充放电循环次数的衰退曲线。

4.2.1相关性分析

将动力电池的充放电数据与容量进行相关性分析并对任意两个相关系数进行显著性检验，根据相关系数的大小选取与容量具有显著强相关的参数作为动力电池性能衰退的特征参数。特征参數与容量（ C ）的 Spearman 相关性系数，如表2所示。由表可知，所有的相关系数均高于0.8，表明所提取的特征参数与容量均有强相关性。

综上提取放电起始总电压（Us ）、系统单体电压差（Ud）、放电末端总电压（Uo ）、放电深度（DOD）、最大回馈电流（Ir ）、最大放电电流（Im ）6个参数，共同作为动力电池性能衰退的特征参数。

4.2.2阈值去噪

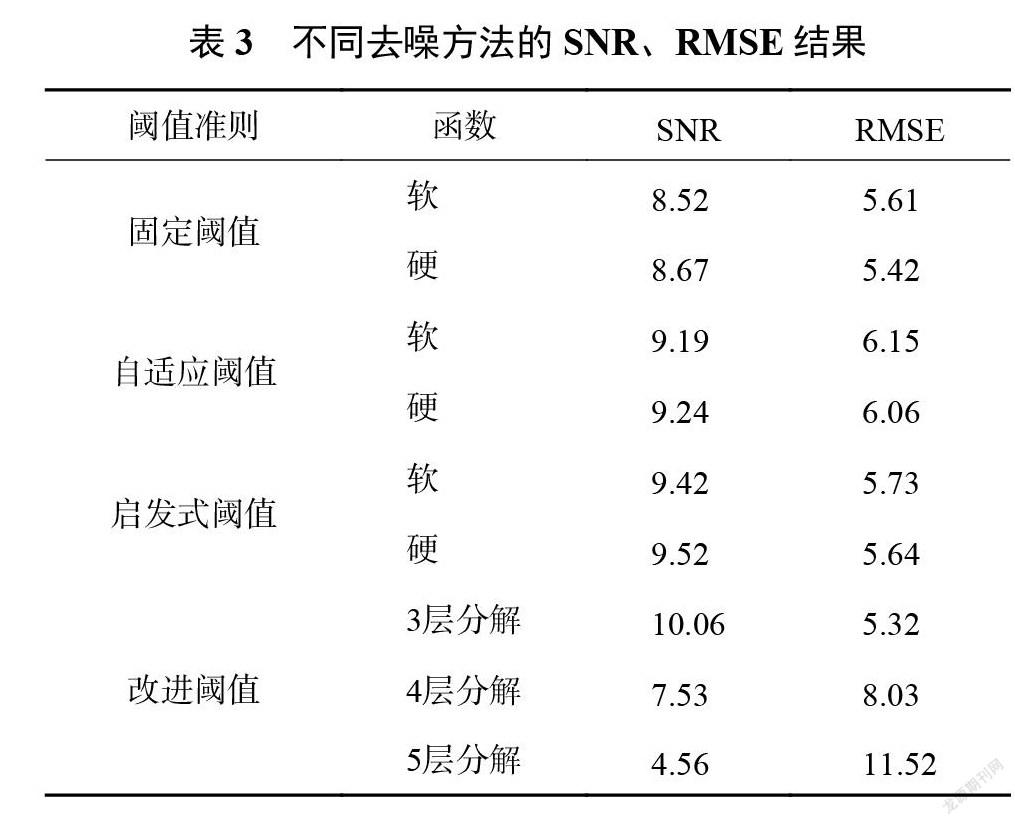
以郑州市的运行数据为例，采用小波变换（wavelet transform，WT）对其特征参数Us、Ud、Uo、DOD、Ir及Im进行去噪，图3为其特征参数去噪前后对比图。由图可知，利用 WT 可有效去除特征参数的噪声干扰，并保持特征参数的原有特征。分别采用如表3所示的4种阈值设定准则对特征参数进行去噪，得到不同降噪方法的 SNR、RMSE 结果，改进阈值去噪法对特征参数具有更高的 SNR 和更低RMSE，去噪效果最好，但随着分解层数增大至4和5层， SNR 减小，出现过去噪，得到的数据信号失真。

4.2.3主成分分析

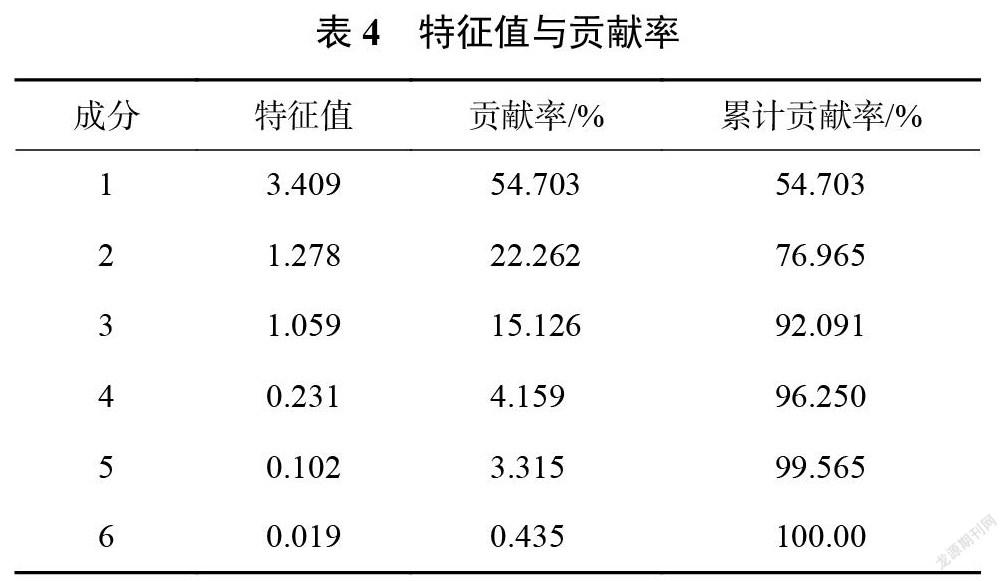
为去除特征参数间的冗余信息，利用 PCA 对去噪后的特征参数进行降维、去除冗余处理，如表4所示。由表可知，前3个主成分的累计贡献率已超过90%，能够充分代表6个特征参数信息，故将前3个主成分作为动力电池的融合特征因子，进行动力电池 RUL 预测。

为验证前3个主成分作为电池融合特征因子的合理性，分别对3个城市的前3个主成分和容量进行相关性分析及显著性检验，如表5所示。由表可知，融合特征因子与容量显著强相关。

4.3结果分析

4.3.1不同预测起点下的预测结果

为验证小波变换对特征参数去噪的有效性，以及评估训练样本数量对预测模型精度的影响，以郑州市纯电动客车的365个充放电循环的动力电池历史运行数据为例，分别将其前200、250和305个充放电循环作为训练集，其余作为测试集进行验证。预测结果如表6所示。

由表6的预测结果可知，GA-SVR 模型能够根据 BMS 易监测的特征参数准确预测出动力电池的容量衰退轨迹，且随着训练样本的增加，模型预测精度不断提高。其中 GA-WT-SVR 模型相比 GA- SVR 模型的训练误差 RMSE 和 MAPE 均值分别减小了71.66%和65.36%，预测误差分别降低了68.96%和65.83%，验证了WT 能够有效去除采集数据中的干扰信号，进一步提高模型的预测精度。

4.3.2不同环境下的电池预测结果

为验证动力电池 RUL 预测模型在不同环境下的准确性和适应性，分别利用在哈尔滨、合肥及郑州3个城市的电池运行数据进行验证，并将对应条件下3个电池分别命名为 A1，A2和 A3。分别将电池的前250个充放电循环作为 GA-SVR 模型的训断变化，在每年的1、2月份，环境温度是全年最低，合肥与郑州的温度相差不大，容量只有额定容量的96.56%左右，哈尔滨的温度较低，容量只有额定容量的95.05%;在每年5、6月份，环境温度适宜，动力电池工作效率高，电池容量保持在98.37%左右;郑州、合肥在每年的8、9月份是一年中温度较高的季节，容量会有所下降，而哈尔滨属于极寒地区，夏季温度不会超过电池适宜温度，容量没有出现下降趋势，随着的周期性变化，动力电池容量不是严格单调，具有一定的弹性复原能力。

由图 4 及表 7 的预测结果可知： 1）在 3 个不同环境下，GA-SVR 模型和 GA-WT-SVR 模型预测误差分别控制在 0.713～0.830 和 0.153～0.356，表明所提出的融合特征因子能够比较全面包含电池的衰退信息，动力电池容量预测模型具有较高的准确性和泛化性;2）预测结果验证了利用 WT 处理后的融合特征因子，能够在保留电池参数原有特征的基础上，去除采集过程中的噪声信号，进一步提高电池预测模型的精度及泛化性，MAPE 和 RMSE 的平均预测误差分别降低了 69.37% 和 63.28%。

5结束语

本文提出了一种基于多特征融合的动力电池RUL 预测方法，通过实验得出结论如下：

1）对于同一批动力电池，在不同的运行环境温度下，动力电池的容量衰退曲线变化趋势不同，温度过高或者过低，容量有所下降，随着环境温度改变，容量有一定弹性恢复能力。

2）所提取的融合特征因子，能够包含动力电池退化的主要信息，能够准确预测出动力电池的容量衰退轨迹。

3）使用 WT 能够有效去除动力电池在采集过程中的噪声干扰，采用去噪后的融合特征因子，相比去噪前的模型预测误差降低60%以上。

参考文献

[1]熊瑞.动力电池管理系统核心算法[M].北京：机械工业出版社， 2018：6-19.

[2] YUJ. Stateofhealthpredictionoflithium-ionbatteries：Multiscale logic regression and Gaussian process regression ensemble[J]. Reliability Engineering & System Safety， 2018，174：82-95.

[3] MA Y， RU J， YIN M， et al. Electrochemical modeling andparameteridentificationbasedonbacterialforaging optimization algorithm for lithium-ion batteries[J]. Journal of Applied Electrochemistry， 2016， 46（11）：1119-1131.

[4]庞辉.基于电化学模型的锂离子电池多尺度建模及其简化方法[J].物理学， 2017， 66（23）：312-322.

[5] JOKAR A， RAJABLOO B， DESILETS M， et al. Review ofsimplifiedP- -seudotwoDimensionalmodelsoflithium-ionbatteries[J]. Journal of Power Sources， 2016， 327：44-55.

[6]黄凯， 郭永芳， 李志刚.考虑迟滞效应影响的动力锂离子电池特性建模[J].电网技术， 2017， 41（8）：2695-2702.

[7]孙朝晖， 成晓潇， 陈冬冬， 等.计及非线性容量效应的锂离子电池混合等效电路模型[J].电工技术学报， 2016， 31（15）：156-162.

[8] WANG MD，IAO Q， PECHT M. Prognostics of lithium-ionbatteries based on relevance vectors and a conditional three- parametercapacitydegradationmode[J]. Journalof PowerSources， 2013， 239（10）：253-264.

[9] REZVANIM，LEES，LEEJ. Acomparativeanalysisoftechniques for electric vehicle battery prognostics and health management （PHM）[C]// SAE Technical Paper， 2011.

[10]郝旭东.基于 RVM-PF 的卫星关键部件寿命预测[D].长沙：国防科学技术大学， 2011.

[11]王瀛洲， 倪裕隆， 郑宇清， 等.基于 ALO-SVR 的锂离子电池剩余使用寿命预测[J/OL].中国电机工程学：1-12[2020-12-

19].http：//kns.cnki.net/kcms/detail/11.2107.TM.20200427.1423.009.html.

[12]陈万， 蔡艳平， 苏延召，等.基于改进粒子滤波的锂离子电池剩余寿命预测[J/OL].中国测试：1-6[2021-03-01]. http：// kns.cnki.net/kcms/detail/51.1714.TB.20201013.1139.002.html.

[13] WU J， ZHANG C， CHEN Z. An online method for lithium-ion batteryremainingusefullifeestimationusingimportance sampling and neural networks[J]. Applied Energy， 2016， 173：134-140.

[14] LIU D， ZHOU J， LIAO H， et al. A health indicator extraction andoptimizationframeworkforlit-hiumionbattery        .degradationmodelingandprognostics[J] IEEE Transactions Systems， Man， and Cybernetics：Systemson， 2015， 45（6）：1-1.

[15]杨帆， 茅丰， 曹岑.基于粒子滤波改进算法的锂动力电池散热特性测试研究[J].中国测试， 2020， 46（7）：102-107.

[16]纪常伟， 潘帅， 汪硕峰， 等.动力锂离子电池老化速率影响因素的实验研究[J].北京工业大学学报， 2020， 46（11）：1272-1282.

[17]王健雁， 廖成龙， 凌泽.锂离子电池的循环寿命影响因素研究进展[J].化工新型材料， 2019， 47（S1）：33-35.

（編辑：莫婕）