工业 CT 系统几何参数校正
2021-09-13陈志祥须颖石锦洋
陈志祥 须颖 石锦洋

摘要:工业计算机断层成像技术(computer tomography,CT)系统几何参数不准确会影响重建图像的质量和尺寸测量的精度。为校正工业 CT 几何位姿失配参数,提出基于标准球板模体的几何校正方法。首先,利用球板在两个不同位置的投影图求解出射线源到探测器的距离以及射线源到运动平台的距离。再在360°范围内间隔一定角度均匀采集球板投影信息,拟合球心投影轨迹,解析求解探测器偏角η、φ和探测器中心点坐标。最后根据重建出的体素模型的球心距测量结果,利用牛顿迭代法,以工业 CT 尺寸测量最大允许误差为约束条件迭代求解探测器偏角θ。实验结果显示:该文幾何校正方法可以求解出所有工业 CT 几何位姿失配参数。参数校正后,提升图像质量,消除重建图像伪影,且工业 CT 球心距测量最大误差由44.8μm 降低到16.3μm,表明该几何校正方法可以满足实际工业 CT 系统校正的要求。
关键词:工业 CT;几何校正;校正模体;图像重建
中图分类号: TP391.4文献标志码: A文章编号:1674–5124(2021)12–0023–06
Geometric parameter calibration of industrial CT system
CHEN Zhixiang,XU Ying,SHI Jinyang
(School of Mechanical and Electrical Engineering, Guangdong University of Technology, Guangzhou 510006, China)
Abstract: Incorrect geometric parameters of the industrial CT (computer tomography) system will affect the qualityof thereconstructedimageandtheaccuracyof dimensionalmeasurement. Inordertocalibrate geometric mismatching parameters of industrial CT, a geometric calibration method based on the standard spherical plate phantom was proposed. Firstly, the distance from the ray source to the detector and the distance from the ray source to the rotating platform were calculated by using the projection of the spherical plate at two different positions. Then, the projection information of the spherical plate was uniformly collected at a certain angle interval within 360° range, fitted the sphere center projection trajectory, and the detector deflection angle η , φ and the detector center point coordinates were calculated analytically. Finally, based on the spherical- center distance measurement results of the voxel model, the Newton iteration method was used to solved the detectordeflectionangle θ bytakingtheMaximumPermissibleErrorof theindustrialCTdimensional measurementastheconstraintcondition. Theexperimentalresultsshowedthatthegeometriccorrection method could solved all the geometric position mismatch parameters of industrial CT. After the parameters were calibrated, the image quality was improved, and the reconstructed image artifacts were eliminated. The maximum error of industrial CTspherical distance measurement was reduced from 44.8μm to 16.3μm,indicated that the geometric calibration method could met the requirements of actual industrial CT system calibration.
Keywords: industrial computer tomography; geometry calibration; calibration phantom; image reconstruction
0引言
工业计算机断层成像技术( computer tomography,CT)是一门集光学、机械、控制和计算机科学于一体的数字化 X 射线成像技术,其利用物体对 X 射线吸收率的不同来获取物体的多角度投影图,并根据这些投影图重建出物体的三维图像[1]。目前这项技术正在向尺寸测量领域发展,但因为工业 CT 通常采用 FDK 算法对投影数据进行重建,而 FDK( Feldkamp-Davis-Kress)算法要求工业 CT系统几何位姿满足理想条件[2],实际情况下,工业 CT 系统难于满足理想条件,系统几何参数会存在偏差。在图像重建过程中,如果不进行校正,会影响工业 CT 尺寸测量的精度。
针对这个问题,Noo[3]利用其设计的两点模体,通过获取模体多角度的投影数据,拟合椭圆运动轨迹,根据椭圆的相关参数求解系统几何参数,在忽略探测器偏角θ对其他参数的影响的情况下,精确求解其余参数,但实际工业 CT 系统中偏角θ是一定存在的,且也会影响图像的重建质量。Jacobson[4]设计了一种金属丝校准模型,利用两条不共面的直线在不同角度的投影平面内的交点位置的不同,根据这些交点的轨迹来计算出系统几何参数,但该方法需要准确知道校正模体中每一根金属丝准确的空间位置,在实际过程中,很难精确定位空间中金属丝的位置,且對空间中金属丝线位置测量的难度明显高于球板球心位置测量的难度。Zhao[5]利用含有九个标准球的正方形模体,采集模体单个角度的投影数据,根据标准球的投影位置关系迭代求出系统几何参数,虽能通过迭代求解出系统所有的失配参数,但该方法仅根据球板一个位置的投影关系求解,其求解精度难以保证。目前,工业 CT 系统参数校正的方法[6-14]都是利用特定校正模体,采集模体不同角度的投影数据,根据投影数据建立起与工业CT 系统几何位姿参数的映射关系,再求解出相应的参数。
本文采用高精度球板模体,采集球板模体在不同角度,不同位置下的二维投影图,求出不同情况下球板各球体球心在探测器上的投影坐标,拟合运动轨迹,再根据投影关系,利用解析法精确求解除θ外的失配参数。之后,用带参数的 FDK 重建算法软件重建出的球板三维图像,将其导入可视化软件 VG Studio MAX 3.0中并提取边缘,测量球体球心距,分析工业 CT 测量误差,以工业 CT 尺寸测量最大允许误差为约束条件,利用牛顿迭代法求解系统最后一个失配参数。相较于其他校正方法,本方法可求解出工业 CT 系统所有的失配参数,且用工业 CT 尺寸测量误差来对比校正前后的效果,更为直观。
1工业 CT 系统和几何参数
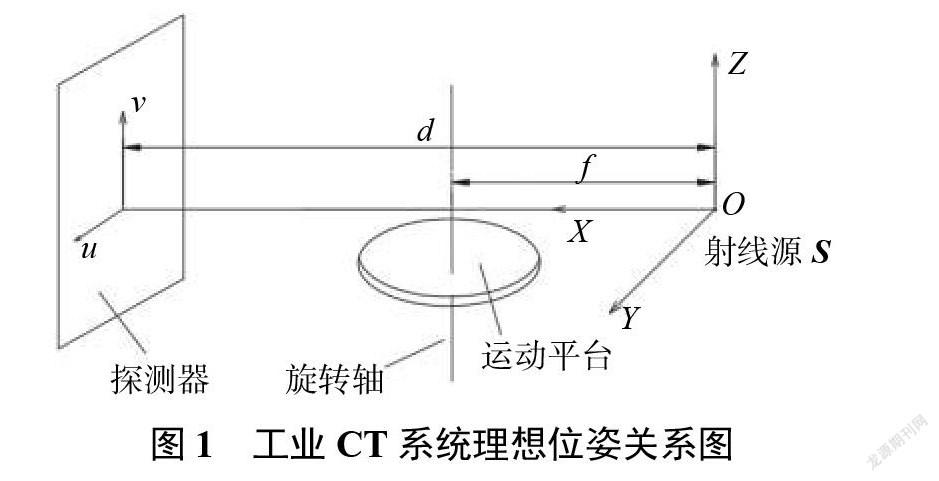
工业 CT 系统主要由射线源、旋转平台和探测器构成,根据 FDK 算法的要求,理想的工业 CT 系统几何结构应满足:射线源焦点和探测器中心点的连线经过旋转轴,且垂直于探测器平面;旋转轴与探测器中心列平行。工业 CT 系统理想位姿关系如图1所示。其中f 为射线源到旋转轴的距离;d 为射线源到探测器中心的距离;(u0 , v0)为射线源焦点在探测器上的垂直投影点。
为更好地研究工业 CT 系统的几何位姿关系,建立三维坐标系O? XYZ,如图1所示。X 轴沿射线方向;Y 轴沿水平方向垂直于射线方向且与探测器中心行平行;Z 轴由右手坐标系原则确定。同样在探测器所在平面上建立二维坐标系O?uv,u 轴沿探测器中心行方向;v 轴沿探测器中心列方向。工业 CT 系统在安装调试过程中,系统位姿关系一定会存在偏差,工业 CT 的校正即校正这些参数。经国内外众多研究人员对工业 CT 校正的研究,需要校正的参数可概括为:探测器绕 X、Y、Z 轴的转动角度η、θ、φ;射线源焦点在探测器上的垂直投影点(u0 , v0)和在 u、v 方向上的偏移Δu、Δv;源到旋转中心的距离以及源到探测器中心的距离。其中和探测器有关的5个参数如图2所示。
2参数校正
2.1校正模体
本文使用的校正模体是球板标准器,如图3所示,由12个高精度的红宝石球体和碳纤维平板组成,部分球体之间的球心距已知。
2.2计算d、f
在保持管电压、管电流和曝光时间等扫描参数不变的情况下,仅改变探测器到运动平台的距离,采集两组不同位置时的球板二维投影图。拟合球板各球体在二维投影图上的圆心位置,再计算圆心距 L,L 为像素数量与像素大小的乘积,即
式中:L——被测量,mm;
n——像素数量;
M——放大比;
D——像元尺寸,mm。
根据式(1),利用上述采集的两组投影图数据,利用球板各球体间球心距,即可建立多个关于 d 和 f 的二元一次方程,在精确知道运动平台沿射线源方向上的运动距离的情况下,可求解出多个 d、f值,最后取 d、f 的平均值作为最终校正结果。
2.3计算η、u0、v0
采集 N(N 为偶数)张1号球和12号球每隔一定角度的投影图,计算出1号球和12号球在不同角度投影图下的球心位置(ui , vi)(i =1, 2,3, ··· , N)。并根据这些球心坐标拟合运动轨迹,可以得到两个椭圆(椭圆1和椭圆2),拟合出的椭圆可用椭圆方程式表示如下:
式中:( , )——椭圆中心点坐标;
a、b、c——椭圆方程参数。
由式(3)分别计算出1号球和12号球球心连线在每隔180°投影图下的中心点位置(1 , 1)、(2 , 2),如图4所示。
其中j = i+ N/2;i =1, 2, ··· , N/2。
探测器面内扭转角η即可由式(4)计算得出。探测器平面内射线源焦点的垂直投影点(u0 , v0)可由式(5)、(6)计算出。
2.4计算φ
Sun[15]等利用四球模体校正系统几何参数,提出平行于转轴的两球投影圆心距之间满足以下关系:
式中:——平行于转轴的两球投影圆心距,
——实际圆心距,mm。
根据这一原理,将 1 号球到 10 号球的球心距和 3 号球到 12 球的球心距 SD3-12 代入式 (7),可计算出。
2.5 计算
根据上述计算出的探测器失配参数对在理想坐标系下的 1 号球球心坐标进行坐标变换得,则:
其中:
经过坐标变换后得到:
射线源焦点坐标S =(0, 0, 0)经坐标变换后,射线源焦点在理想坐标系下的坐标应为S\=(xs ,ys ,zs);将 S\与p 相连交探测器于点p = v \),p \即为1号球球心经 X 射线投射后在探测器上的投影点。其中:
同理可計算出其他球体球心经 X 射线投射后在探测器上的投影点坐标。
此时使用带参数的 FDK 重建算法软件,利用上面所计算出的6个系统失配参数,重建出此时球板模体的三维图像,再利用 VG Studio MAX 3.0图像可视化软件测量各球体间的球心距,找出此时球心距误差最大的两球体。以1号球和12号球为例,此时两球球心在探测器上的投影点间距离为:
式(12)中,除θ外的其他参数均已知,故S D1?12= f (θ)是一个关于θ的函数,解析求解过于复杂,可用牛顿迭代法求解,以工业 CT 尺寸测量最大允许误差为迭代约束条件,迭代求解出θ。
3实验验证
3.1实验设备及参数
为验证上述方法的可行性,在实际工业 CT 系统中进行了实验,实验所使用的设备为天津三英精密仪器有限公司生产的 nanoVoxel-4000,如图5所示。射线源为开管发射式,最大管电压为220 kV,最大管电流为1.0 mA;探测器成像面积为427 mm ×427 mm,像素矩阵为3072×3072;像素细节分辨力为500 nm,空间分辨率为2?m。
3.2校正过程
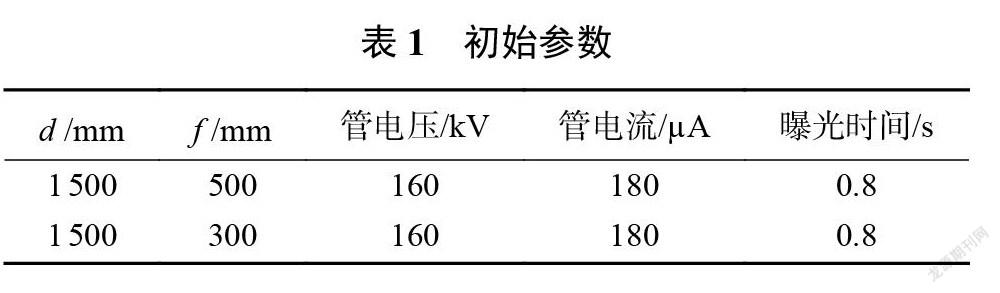
首先验证 d 和f,在 d 固定的情况下,改变f其他参数如表1所示,采集两组投影图。表1 初始参数
通过计算可得,射线源到探测器的距离误差为–5.2029 mm,射线源到旋转轴的距离误差为–4.3907 mm。
在调整工业 CT 系统 d 和f后,再次扫描校正模体,保持 d=1500 mm,f=500 mm,在其他参数不变的情况下360°范围内采集球板模体的投影图,然后根据本文方法求解圆心,拟合椭圆轨迹如图6所示,椭圆参数计算出工业 CT 其余几何参数,最后利用迭代法经4次迭代后计算出工业 CT 需校正的最后一个参数。
至此,所有参数校正完毕,最终校正结果如表2所示。
3.3校正前后效果对比
实际重建过程中,利用带参数的 FDK 重建算法软件重建球板模体,校正前后的重建图像对比如图7所示,可以看出,校正后球板模体的重建图像质量有了明显提升,消除了图像伪影,提升了图像清晰度。
利用 VG Studio MAX 3.0图像可视化软件分别对校正前后重建的球板模体三维图像进行尺寸测量,两次测量结果如图8所示。可知校正后工业 CT 尺寸测量的最大误差由44.8?m 降低到16.3?m,效果明显,本文工业 CT 系统参数校正的方法降低了工业 CT 尺寸测量的误差。
4结束语
本文基于高精度球板模体,提出了一种工业 CT 几何参数校正的方法,利用球板在不同角度下的投影图像,获取球心投影运动轨迹,拟合椭圆,再根据椭圆参数和工业 CT 尺寸测量的最大误差,结合解析法与迭代法,可求解出工业 CT 系统所有几何失配参数。实验表明,校正后重建图像的质量有了明显的提升,减少了图像伪影,校正后工业 CT 尺寸测量最大误差由44.8?m 降低到16.3?m,能满足实际工业 CT 系统参数的校正要求。但是,本文几何校正方法需要高精度的校正模板,需要准确知道球板模体各球心距,也受限于运动平台回转精度和沿射线源方向的运动精度,否则会影响校正参数的准确性。
参考文献
[1]张朝宗.工业 CT 技术和原理[M].北京:科学出版社, 2009.[2] FELDKAMP L A, DAVIS L C, KRESS J W. Practical cone-beam algorithm[J]. Journal of the Optical Society of America A, 1984, 1(6):612-619.
[3] NOO F, CLACKDOYLE R, MENNESSIER C, et al. Analyticmethodbasedonidentificationofellipseparametersfor scanner calibration in cone-beam tomography[J]. Physics in Medicine and Biology, 2000, 45(11):3489-3508.
[4] JACOBSON M W, KETCHA M D, CAPOSTAGNO S, et al.A line fiducial method for geometric calibration of cone-beam CTsystemswithdiversescantrajectories[J]. Physicsin Medicine and Biology, 2018, 63(2):025030.
[5] ZHAO J T, HU X D, ZOU J,etal. Geometric parametersestimationandcalibrationincone-beammicro-CT[J]. Sensors, 2015, 15(9):22811-22825.
[6]周凌宏, 李翰威, 徐圆, 等.锥束 CT 圆轨道扫描的几何校正[J].光学精密工程, 2014, 22(10):2847-2854.
[7] SMEKALLV,KACHELRIEM,STEPINAE,etal.Geometricmisalignmentandcalibrationincone-beam tomography[J]. Medical Physics, 2004, 31(12):3242.
[8] CHO Y, MOSELEY D J,SIEWERDSEN J H, et al. Accuratetechniqueforcompletegeometriccalibrationof cone-beam computedtomographysystems[J]. MedicalPhysics, 2005,32(4):968-983.
[9] XIANG Q, WANG J, CAI Y F. A geometric calibrationmethodforconebeamCTsystem[C]//EighthInternational ConferenceonDigitalImageProcessing (ICDIP 2016). International Society for Optics and Photonics, 2016.
[10] PATEL V, CHITYALA R N, HOFFMANN K R, et al. Self- calibrationofacone-beammicro-CTsystem[J]. MedicalPhysics, 2008, 36(1):48-58.
[11]张才鑫, 黄魁东, 陈华.基于标定量具的快速锥束 CT 几何校准方法[J].仪器仪表学报, 2019, 40(1):175-182.
[12] ZHOU K, HUANG Y X, MENG X X, et al. A new method for cone-beamcomputedtomographygeometricparameters estimation[J]. JournalofComputerAssistedTomography, 2016, 40(4):639-648.
[13] LI G, LUO S H, YOU C Y, et al. A novel calibration method incorporatingnon-linearoptimizationandball-bearing markers for cone-beam CT with a parameterized trajectory[J]. Medical Physics, 2019, 46(1):152-164.
[14] LI H C, HONG W, LIU Y, et al. A novel method of micro- tomographygeometricanglecalibrationwithrandom phantom[J]. Journal of X-ray science and technology, 2017,25(4):641-652.
[15] SUN Y, HOU Y, ZHAO F Y, et al. A calibration method for misalignedscannercogeometryinne-beamcomputed tomography[J]. NDT and E International, 2006, 39(6):499-513.
(編辑:莫婕)
