基于模糊综合评判和排队论的机场出租车问题研究

李旭 胡鹏鸽 郑飞芳 曹建莉

摘 要：本文对影响机场出租车司机决策的各类因素进行分析，针对放空返回市区或留在机场候客构建合理的决策指标，给出更具实用性和合理性的机场出租车司机决策模型。同时基于排队论原理，给出两种乘车点的规划模型，并通过考察工作指标确定最优上车点数，兼顾机场管理者和乘客的需求，给出更为灵活、适用性强的规划方案。

关键词：出租车司机决策;模糊综合评判;排队论;乘车点规划

Airport Taxi Problem Based on Fuzzy Comprehensive Evaluation and Queuing Theory

Li Xu， Hu Pengge， Zheng Feifang， Cao Jianli （corresponding author）

（College of Science， Henan University of Technology， Zhengzhou， 450001）

Abstract： In this paper， we analyze the factors that affect the decision of the airport taxi driver. Reasonable decision indicators are established for returning to the city without passengers or waiting for passengers at the airport. A more practical and reasonable decision model of the airport taxi driver is given. Meanwhile， based on the principle of queuing theory， we present two boarding point planning models， and give a more flexible and adaptable planning scheme to determine the optimal number of boarding points by examining the work indicators and considering the needs of airport managers and passengers at the same time.

Key words： Taxi driver decision making; Fuzzy comprehensive evaluation; Queuing theory; Boarding point planning

1 引言

对机场出租车司机来说，选择放空返回市区或留在机场候客，是一个重要的决策问题。对运输管理部门而言，合理规划出租车的上车点也是现代交通发展的必然要求。

在机场出租车司机决策问题中，有学者得出蓄车池中等待车数比乘客数影响程度更大[1];更多研究以收益优先为主要目标[2]。在出租车上车点的规划问题上，有学者得到双车道设置3个上车点使乘车效率较高[3]，或基于排队论原理得出最优规划方案[4]。本文基于模糊综合评判模型，结合影响司机决策的各类因素进行分析，给出适用性更广的决策模型;基于排队论思想，综合利用约束分析给出最优上车点方案。

2 机场出租车司机决策模型

考虑到司机决策的目标是利益最大化，无论在机场等待还是放空返回市区载客都需要付出相应时间成本。由于司机每次的收入不易预估，利益最大化需要尽可能降低成本。

2.1  机场出租车司机决策的影响因素分析

一般地，司机是否留在机场载客需综合考虑多种因素，有机场候车乘客数、时间（夜晚乘客坐出租车可能性更大）、机场等待出租车数量（数量过多时，司机更倾向于放空回市区）、天气以及节假日（某些重大节日往往导致机场客流量增加）等因素。

2.2  基于模糊综合评判的机场出租车司机决策模型

由于出租车司机既是决策者，又是执行者，可能有上述5种因素外的特殊情况（如疲憊等）[5]。

首先，建立指标集U={u1， u2， u3， u4， u5， u6}，其中u1=“机场候车乘客数”，u2=“所处时间”，u3=“机场等待出租车数量”，u4=“天气”，u5=“节假日”，u6=“司机自身状态”。其次，为保证尽可能客观地体现一般的影响程度，采用专家评判法确定权重矢量A={a1， a2， a3， a4， a5， a6}，其中。其结果为： A={0.21， 0.20， 0.24， 0.18， 0.10， 0.07}，然后建立决策集V={v1， v2}，其中v1=“在机场等客”，v2=“放空返回市区”。建立评判矩阵，其中是在下的隶属程度，根据可得综合评价集B={b1， b2}，由最大隶属度原则，即可在影响因素相对模糊的情况下，帮助司机做出比较合理的决策。

2.3  应用及分析

以新郑国际机场为例，选取8：00-8：30，15：00-15：30，21：30-22：00三个时间段，随机抽取30名出租车司机进行考证。根据模型，有8名司机返回市区、22名司机留在机场载客，与事实吻合。

3  机场上车点的规划模型

乘客到上车点排队乘坐出租车的过程可视为排队接受服务台服务的过程。由于单服务台在机场、火车站等人流量较大的场所易崩溃，故需考虑兼顾灵活性与工作强度的多服务台系统。

将各上车点视为服务台，等待乘车的乘客视为被服务者。单位时间内到达候车区的乘客数可被视为泊松流，单位时间内各服务台对每一乘客的服务时间服从负指数分布，记各服务台的平均服务率μ。假设单位时间内到达的顾客数为λ，系统内上车点设置有c个，各服务台独立服务。

3.1  单队多点式

考虑到更大限度利用两条并行车道以提高系统服务效率，上车点安置在距离乘客较近的右侧车道，乘客在候车区域可分散成多个纵列排队等待乘车。当每个服务台处的乘客完成上车后，即为完成服务。司机将驾驶到左侧车道上驶出机场，未载客的出租车被放行进入系统，进入原来服务台的位置。该方案可使得系統处于较高效的运行中，而且可以保证乘客就近上车，节省服务时间，如图1所示。

3.2  两队多点式

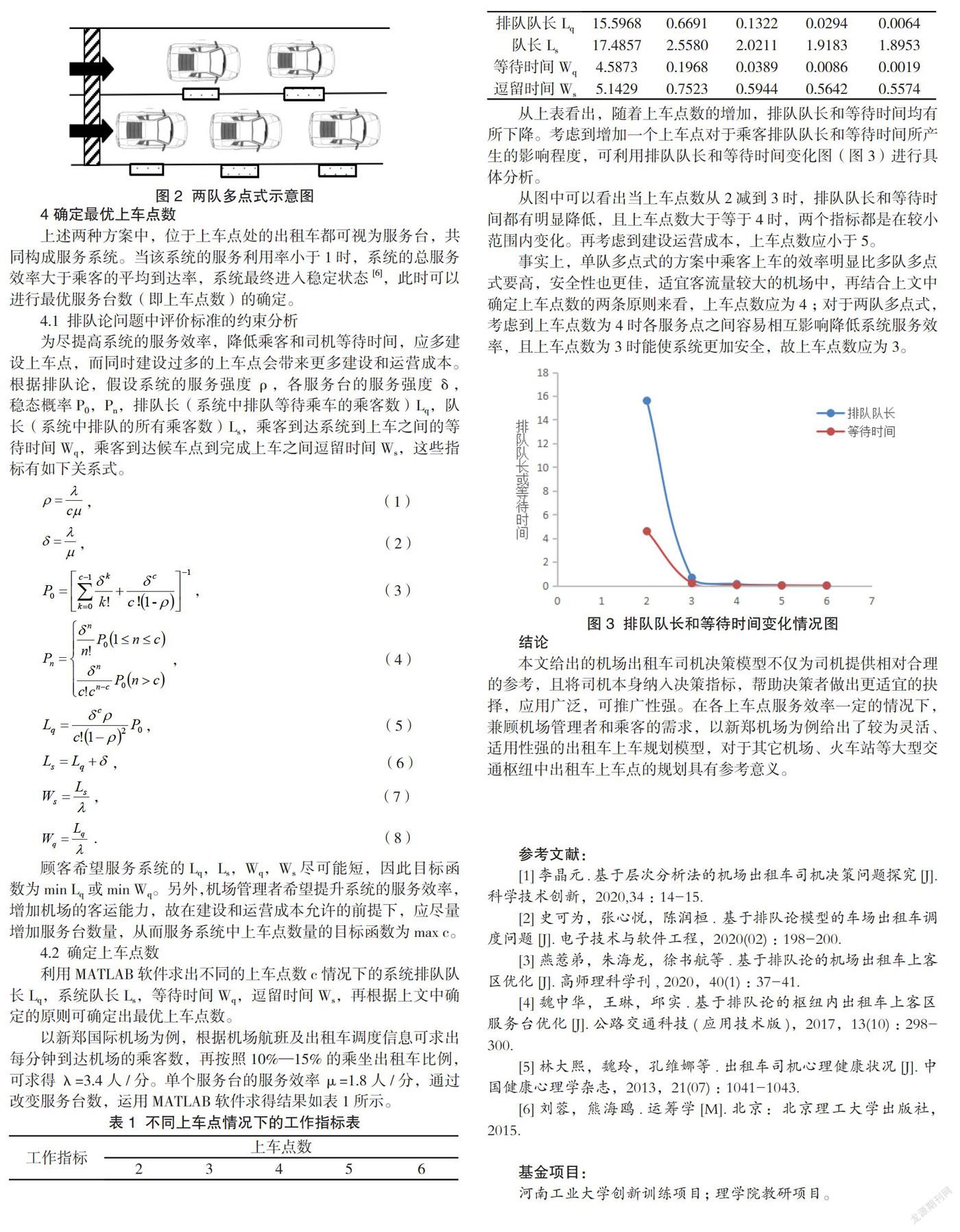
系统的两条车道上共有c辆等待载客的出租车，各上车点处均有乘客排队候车，左右两车道上的出租车都可载客。等到系统内的出租车全部驶离，再继续放行后面未载客的出租车进入系统。为保证安全，系统完成补位过程中乘客只能处于排队候车状态，如图2所示。

4 确定最优上车点数

上述两种方案中，位于上车点处的出租车都可视为服务台，共同构成服务系统。当该系统的服务利用率小于1时，系统的总服务效率大于乘客的平均到达率，系统最终进入稳定状态[6]，此时可以进行最优服务台数（即上车点数）的确定。

4.1  排队论问题中评价标准的约束分析

为尽提高系统的服务效率，降低乘客和司机等待时间，应多建设上车点，而同时建设过多的上车点会带来更多建设和运营成本。根据排队论，假设系统的服务强度ρ，各服务台的服务强度δ，稳态概率P0，Pn，排队长（系统中排队等待乘车的乘客数）Lq，队长（系统中排队的所有乘客数）Ls，乘客到达系统到上车之间的等待时间Wq，乘客到达候车点到完成上车之间逗留时间Ws，这些指标有如下关系式。

顾客希望服务系统的Lq，Ls，Wq，Ws尽可能短，因此目标函数为min Lq或min Wq。另外，机场管理者希望提升系统的服务效率，增加机场的客运能力，故在建设和运营成本允许的前提下，应尽量增加服务台数量，从而服务系统中上车点数量的目标函数为max c。

4.2  确定上车点数

利用MATLAB软件求出不同的上车点数c情况下的系统排队队长Lq，系统队长Ls，等待时间Wq，逗留时间Ws，再根据上文中确定的原则可确定出最优上车点数。

以新郑国际机场为例，根据机场航班及出租车调度信息可求出每分钟到达机场的乘客数，再按照10%—15%的乘坐出租车比例，可求得λ=3.4人/分。单个服务台的服务效率μ=1.8人/分，通过改变服务台数，运用MATLAB软件求得结果如表1所示。

从上表看出，随着上车点数的增加，排队队长和等待时间均有所下降。考虑到增加一个上车点对于乘客排队队长和等待时间所产生的影响程度，可利用排队队长和等待时间变化图（图3）进行具体分析。

从图中可以看出当上车点数从2减到3时，排队队长和等待时间都有明显降低，且上车点数大于等于4时，两个指标都是在较小范围内变化。再考虑到建设运营成本，上车点数应小于5。

事实上，单队多点式的方案中乘客上车的效率明显比多队多点式要高，安全性也更佳，适宜客流量较大的机场中，再结合上文中确定上车点数的两条原则来看，上车点数应为4;对于两队多点式，考虑到上车点数为4时各服务点之间容易相互影响降低系统服务效率，且上车点数为3时能使系统更加安全，故上车点数应为3。

结论

本文给出的机场出租车司机决策模型不仅为司机提供相对合理的参考，且将司机本身纳入决策指标，帮助决策者做出更适宜的抉择，应用广泛，可推广性强。在各上车点服务效率一定的情况下，兼顾机场管理者和乘客的需求，以新郑机场为例给出了较为灵活、适用性强的出租车上车规划模型，对于其它机场、火车站等大型交通枢纽中出租车上车点的规划具有参考意义。

参考文献：

[1]李晶元.基于层次分析法的机场出租车司机决策问题探究[J].科学技术创新，2020，34：14-15.

[2]史可为，张心悦，陈润桓. 基于排队论模型的车场出租车调度问题[J].电子技术与软件工程，2020（02）：198-200.

[3]燕惹弟，朱海龙，徐书航等.基于排队论的机场出租车上客区优化[J].高师理科学刊， 2020，40（1）：37-41.

[4]魏中华，王琳，邱实.基于排队论的枢纽内出租车上客区服务台优化[J].公路交通科技（应用技术版），2017，13（10）：298-300.

[5]林大熙，魏玲，孔维娜等.出租车司机心理健康状况[J].中国健康心理学杂志，2013，21（07）：1041-1043.

[6]刘蓉，熊海鸥.运筹学[M].北京：北京理工大学出版社，2015.

基金项目：

河南工业大学创新训练项目;理学院教研项目。

作者简介：李旭（1998-），女，河南商丘，研究方向为数学与应用数学;胡鹏鸽（1999-），女，河南洛阳，研究方向为数学与应用数学;郑飞芳（1998-），女，浙江衢州，研究方向为数学与应用数学;曹建莉（1971-），女，河南巩义，教授，博士，研究方向为孤立子与可积系统，数学模型。

通信作者：曹建莉