多元函数极值问题的解法研究

徐莉　周创

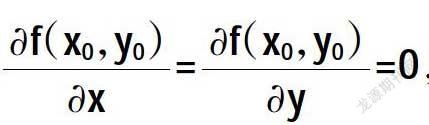
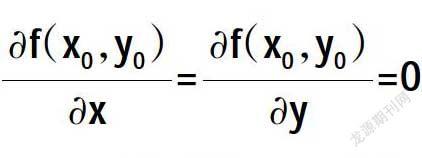
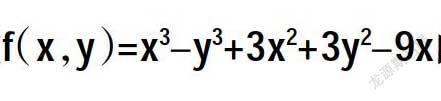
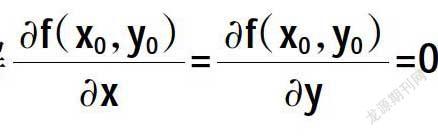
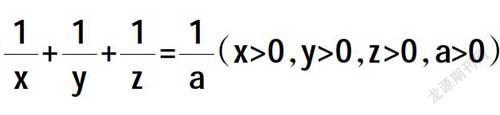
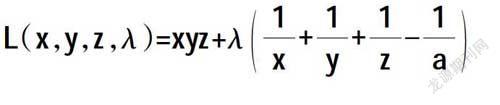
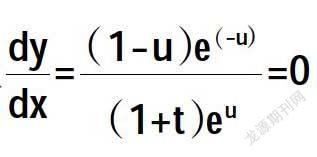
摘  要：近几年，许多学者对多元函数进行了更深入的研究，有关多元函数方面的理论也逐渐完善，应用也越来越广泛。多元函数极值问题的解法通常是研究的重点，故本文也进行了相关的分析和研究，分别是多元函数极值的概念、多元函数极值的判定、条件极值与拉格朗日乘数法以及多元函数极值问题的几种解法，并分别进行了相应的总结。

关键词：多元函数;极值问题;解法

中图分类号：O174.1    文献标识码：A    文章编号：1673-7164（2021）19-0145-04

多元函数从一元函数演变过来，具有一元函数的某些基本性质，也具有自身的一些特性。因此，在研究多元函数时应结合一元函数来研究。解多元函数通常需要研究二元函数[1]。多元函数极值问题的解法通常是研究的重点，当然也是学习高数的重点，通过阅读大量文献以及结合自身学习函数的实践经验，本文对多元函数极值问题的几种解法进行了分析探讨，并进行了相应的总结。

一、多元函数极值的概念

值，也就是指多元函数在给定的范围内或者定义域内的最大值或者最小值。多元函数的极值，是对于二元函数的极值来定义的。假设函数z=f（x，y）的定义域为D，P0（x0，y0）是D内的点，如果存在某个定义域内的领域属于D，该领域内的点与P0不同，但是都存在f（x，y）<f（x0，y0），则称f（x，y）在点P0（x0，y0）处有极大值，点P0（x0，y0）称为函数f（x，y）的极大值点;反之，则称f（x，y）在点P0（x0，y0）处有极小值，点P0（x0，y0）称为函数f（x，y）的极小值点[2]。

假设函数z=f（x，y）在（x0，y0）处具有偏导数，并且在点（x0，y0）处有极值，那么

把该点称为二元函数z=f（x，y）的驻点。如果z=f（x，y）存在偏导数，那么函数的极值点一定是函数的驻点。但是相反地，函数的驻点不一定是极值点。

二、多元函数极值的判定

对于多元函数极值的判定存在必要条件和充分条件，必要条件就是极值所在点是驻点。充分条件为z=f（x，y）在定义域或者某领域包含点（x0，y0）存在二阶导数，且是连续的，如果对x进行二次求导设为A，即fxx（x0，y0）=A，对x再对y偏导数记为B，即fxy（x0，y0）=B，对y二次求导设为C，即fyy（x0，y0）=C[3]。

（1）AC-B2>0，则表明具有极值，且（x0，y0）即为极值点，当A<0时，存在极大值，（x0，y0）点处为极大值，反之，存在极小值，（x0，y0）为极小值;（2）若AC-B2<0，则表明没有极值，即函数在（x0，y0）处不存在极值点;（3）若AC-B2=0，则可能存在极值，也可能不存在极值，即无法判断函数在（x0，y0）处是否存在极值，还需另作讨论。

对于可进行二次求导的连续的z=f（x，y）进行极值点的求解时，教师可引导学生首先对z=f（x，y）的x，y分别进行一次求导，并解，从而会得到多组驻点，要想判断哪个驻点为所求的极值点，可以分别对每个驻点进行二次求导，通过AC-B2的值来判断是否存在极值，若存在极值则进一步判断是极大值还是极小值。

三、条件极值与拉格朗日乘数法

（一）條件极值

对多元函数的概念进行定义时，只需要研究的点在定义域之内，没有其他任何条件，这就是无条件极值，条件极值其实在生活日常的运用中会经常出现，例如下面一道例题：z=f（x，y）=x3y（4-x-y）在由x+y=6，求x轴和y轴所围成的闭区域D上的极值、最大值与最小值。

此题中x+y=6，x轴和y轴所围成的闭区域D就是题目的两个条件，可以将x+y=6，转换为y=6-x，带入z中再研究极值。其实这一步骤是将条件极值转换成了无条件极值进行求解。但是，并不是任何一个有条件的极值求解都可以转换成无条件极值，因此有学者提出拉格朗日乘数法能够对任何一种条件极值题目进行求解。

（二）拉格朗日乘数法

拉格朗日乘数法主要是对存在一个条件或者多个条件的多元函数的极值进行求解。拉格朗日乘数法实质上就是将n个变量与k个约束条件最优解的问题，转换成n+k个变量的方程组的极值问题，从而使得变量不再有约束条件，在转变的过程中引入了拉格朗日乘数[4]。具体定义介绍如下：

假设给定了二元函数z=f（x，y）和条件函数为φ（x，y）=0，要求z的极值。那解答者首先要构建拉格朗日函数L（x，y）=f（x，y）+λφ（x，y），其中拉格朗日乘数就是λ，分别对x，y进行求导，使其值为零，并与附加条件联立，即

L′x（x，y）=f ′x（x，y）+λφ′x（x，y）=0

L′y（x，y）=f ′y（x，y）+λφ′y（x，y）=0

φ（x，y）=0

根据这三个方程求解出x，y，λ，这样所求解出的（x，y）就是可能的极值点，要是该点唯一就必然是题目所要求解的点。

四、多元函数极值问题的几种解法

（一）二元导数偏导数求解多元函数极值

如果（x，y）存在二阶连续偏导数，则可以通过二元导数偏导数来求解多元函数极值。具体步骤可以分为三步，第一步是对（x，y）进行求导后，解的方程组，从而得到所有的驻点;第二步是对每个驻点求解相应的A、B、C的值;第三步就是通过判断AC-B2的值从而来判断驻点是否为极值，若为极值，是极大值还是极小值。值得注意的是如果AC-B2=0或者（x，y）不存在偏导数，则需要采取其他的求解办法进行求解。相应的例题如下：求解函数f（x，y）=x3-y3+3x2+3y2-9x的极值

解（1）求解的方程组。求解出所有驻点，分别为（1，0），（1，2），（-3，0），（-3，2）;（2）对于每个驻点求解相应的A，B，C的值;（3）通过判断AC-B2的值从而来判断驻点是否为极值。通过计算得AC-B2<0，则表明（1，2），（-3，0）不是函数的极值点;而在点（1，0）处AC-B2>0，且A的值小于零，这表明（1，0）是所要求函数的极小值点，将（1，0）代函数可得f（1，0）=-5;在点（-3，2）处AC-B2<0，且A的值大于零，这表明（-3，2）是所要求函数的极大值点，将（-3，2）代入函数可得f（-3，2）=31。

至此，本题利用二元导数偏导数求解完毕，得出正确答案。

（二）拉格朗日乘数法求解多元函数极值

前文也有提到过，拉格朗日乘数法实质上就是将n个变量与k个约束条件最优解的问题，转换成n+k个变量的方程组的极值问题，它所要解决的是条件极值的问题，具体的步骤和相关例题如下：求解t=xyz的极值，约束条件为（x>0，y>0，z>0，a>0）。

解（1）构建拉格朗日函数。

（2）分别对x，y，λ进行求导使其值为零。即，可以求解出x=y=z=3a，因此解答者可以得出t=xyz的极值点为（3a，3a，3a），再加上这个极值点唯一，因此本题的极值点一定存在，将（3a，3a，3a）代入t=xyz，可得极值为27a3。

上题中如果想严格地确定所求出的点（3a，3a，3a）是否真的为极值点，解答者可以将z用x，y，a表示出来，带到t=xyz中，从而得到一个二元函数，再用二元函数求解多元函数的极值进行求解，上节关于二元函数求解多元函数极值的方法和步骤已经有详述，此处不做过多赘述。

（三）参数方程求解多元函数极值

求函数z=f（x，y）的极值点，x=ueu，y=ue（-u）。

解dy=（1-u）e（-u）;dx=（1+t）eu，让，求解可得u=1，驻点为x=e。经过分析可以得出，当u<1，也就是在x=e的左侧时，y的导数大于零，函数递增;当u>1，也就是在x=e的右侧时，y的导数小于零，函数递减;这可以证明x=e处为函数的极大值点。

在对此题进行思考和作答时，值得注意的是，当dx=0，即u=-1，此时函数是没有意义的，当u=-1，x=ueu时，解答者对其求导可得，二次求导后可得其值大于零，根据定义可以看出u=1是x=ueu的极小值点，此时，这是z=f（x，y）的左端点，并不是所谓的极小值点，因为函数极值有定义，极值点是定义区间的内点。

五、总结

综上所述，本文简单介绍了多元函数的概念、多元函数极值的判定、条件极值与拉格朗日乘数法，并介绍了多元函数的三种常见的解法，在实际解决问题或者解决题目时，可以具体情况具体分析，找到适合的方法和手段，更快地解决问题[5]。

参考文献：

[1] 牛艳秋. 求解多元函数极值与条件极值的探讨[J]. 黑龙江科学，2018，9（18）：14-15.

[2] 佘連兵. 多元函数极值问题的概念及理论应用[J]. 六盘水师范学院学报，2016，28（03）：5-10.

[3] 范周田，彭娟，黄秋梅. 多元函数极值充分条件证明的一元方法[J]. 数学的实践与认识，2015，45（24）：297-300.

[4] 荆庆林. 基于求多元函数极值应注意问题的研究[J]. 吉林工程技术师范学院学报，2013，29（04）：67-70.

[5] 李安东. 多元函数极值和条件极值的一般判定方法[J]. 皖西学院学报，2006（02）：30-33.

（荐稿人：陶立平，金华广播电视大学副教授）

（责任编辑：汪旦旦）