基于“抛-析-探-炼-解-拓”六位一体的 计算方法课程教学改革
2021-09-10郝辉李雪瑞李亚雄
郝辉 李雪瑞 李亚雄


摘 要:针对“计算方法”课程内容抽象、公式繁多、理论实践并重等特点,本文基于教师多年的教学经验,提出了“抛-析-探-炼-解-拓”六位一体的教学方法,以“二分法”为例,详细说明了该方法的具体实施过程。实践证明,该方法以学生为主体,改变了传统的教师主导教学模式,激发了学生的学习热情和课程参与度,有助于内容知识的传授和科研精神的培养。
关键词:计算方法;教学改革;六位一体;二分法
中图分类号:G642.3 文献标识码:A 文章编号:1673-7164(2021)19-0025-07
计算方法课程是高等院校诸多理工类专业、数学类专业的基础课程,也是火箭军工程大学火力指挥与控制工程专业的基础课程之一。该课程目标主要是使学生熟悉掌握数值科学计算的基本思想、主要内容和实现过程,逐步培养学生独立思考、分析问题、编程实践的能力,能够将数值方法与实际问题相结合以求取其数值近似解,为后续专业课程的学习奠定基础,并为其将来走上科研岗位进行科学实验与计算提供有力支撑[1-2]。
计算方法课程涵盖数学知识多、公式复杂,传统教学中单一的理论传授式讲课,学生极易出现枯燥乏味的感觉,也会产生难于理解、困于应用的现象[3]。知识源于生活并服务于生活,教师应从日常生活中发现学生的兴趣点,挖掘生活中的知识点,带领学生对问题进行探讨,运用趣味式的互动方式,并借助现代教学手段,适当调整教学方法,以达到师生协同探索、合作共进的教学目的[4]。为此,本文提出了“抛-析-探-炼-解-拓”六位一体的教学方法。
一、课程特点及教学问题剖析
作为一门专业基础课程,计算方法课程主要为学科研究过程中一些无法解决的数学问题提供数值近似解的方法。该课程既呈现出数学基础课程的特点,又具有广泛的应用领域。其主要特点如下:一是知识面广,理论性强,既涉及高等数学的泰勒级数、常微分方程求解等,又涉及线性代数的线性方程组求解、矩阵特征值计算等相关理论知识;二是应用面广,实践性强,目前,业界对于数值计算在气象、地震、核能技术、石油勘探、航天工程、密码解译等领域有着重要的地位已达成共识[1]。
为此,课程教学中除了介绍各种数值算法的基本原理和数学基础,更应该强调算法的实现和应用,要求学生利用相关工具,对所处理的问题构造合理的计算方法,同时研究算法的有效性、收敛性及稳定性等。
基于计算方法课程特点,老师在授课过程中经常会存在些许困难或局限性,主要体现在以下几个方面[5]:
一是重传授,轻互动。课程内容多、学时少,是授课老师面临的最大困难。教师迫于完成教学任务,如果采用传统的满堂灌授课方式,课堂上缺乏互动或互动极少,无暇顾及学生对知识的掌握情况,这样容易导致学生学习状况的两极分化。
二是重理论,轻实践[6]。教材原理多、应用少,是一些计算方法教材的不足之处。由于教学经验的匮乏,一些老师只注重讲授书本上的理论知识,花大量时间去进行烦琐的定理证明和公式推导,而忽略实践环节的教学,致使学生虽掌握了书本上的理论知识,但对实践环节了解甚少,这样,极易出现高分低能的现象。
三是重验证,轻探索。课程算例多、案例少,是授课过程中的常见问题。疏于对专业知识的理解,诸多老师课堂上仅仅局限于书本上的算例,缺乏对日常生活的留意观察,因而实践环节只是安排少数的或者传统的算例,对贴切生活实例和典型的专业案例介绍得少之又少,从而导致学生探索能力的不足和创新精神的欠缺。
二、学生特点及存在问题分析
通常情况下,计算方法课程开设在大学二年级的第二学期。此时,学生通过前期高等数学、工程数学、计算机软件基础等课程储备了该课程相关的基础知识。研究发现,大二年级中的大部分学生学习积极、思维活跃、互动参与期待高,具有突出优势和明显不足。
(一)爱探索、爱合作、爱专业
大二年级的学生饱含对大学学习的新奇和热情,开始进入对学科领域的探索阶段,积极参与学校组织的一些俱乐部活动,也勇于承担学科专业的创新课题,同学之间也愿意合作去完成对未知问题的探讨和研究。
(二)重知识、重考试、重运用
首先,知识是学生时期重要的收获,对知识的理解和掌握程度是以后走上工作岗位的有效支撑。大学期间学生需要完成诸多基础课程和专业课程的学习,课程考核的成绩直接关乎每位学生的切身利益。其次,如何有效运用所学知识解决实际问题?所学知识在未来工作岗位中发挥的作用又如何?诸如这一系列现实问题都是他们所关心的话题。
(三)怵公式、怵推导、怵应用[7]
計算方法课程与数学知识紧密相连,教材里涉及数学公式繁多,公式推导证明复杂,学生极易产生畏难情绪和恐惧心理,尤其是一些数学基础偏弱的学生。教师在授课过程中若只介绍一些经典理论和算法,实例演示和案例探讨偏少,会使得学生对课程的理解和应用知之甚少,也会盲目地去学习。
三、课程设计及教学方法改革
(一)课程设计
根据本校人才培养方案要求和课程标准规定,计算方法课程学时数为40学时,其中包含6学时的课程实践。考虑课程学时数量,结合专业需要和学生特点,将课程教学内容分为六大模块:“方程的近似解法”“线性方程组的解法”“插值法”“最小二乘法与曲线拟合”“数值微积分”和“常微分方程解法”。教师应将课程的重点放在算法模型的建立、构造与试验,核心集中在相关专业领域的应用建模。整个教学过程中,从计算方法的一般原则出发,针对不同类型的数学问题,分别展开探讨各数值计算方法;课程内容设计方面,应紧密贴合日常生活和实际应用,加强理论知识和实践应用的融合,注重培养学员分析问题、解决问题的能力,全面提高学生的科研精神和创新能力。
(二)教学方法改革
针对课程特点和学生状况,计算方法课程需注重传统与现代相结合,课内与课外相结合,融理论与实践于一体,对复杂的算法思想进行探索提炼,抽象的理论知识采用趣味生动的方式进行讲解阐述,通过现代信息技术实时掌握学生的学习情况,并及时调整教学进度和授课方式,从而全方位地提高课堂授课质量,增强学生学习效果[8-9]。为此,本文提出了以“学员讨论为主、教员教学为辅”的教学策略,集“抛-析-探-炼-解-拓”六位一体的教学方法。教学实施过程中,借助现代信息技术手段,采用“逐步探究、层层剖析”的教学方式,引导学生一起去探索知识,发现知识中存在的问题,同时结合实例展开教学。
下面就以“二分法”为例,详细说明六位一体教学方法的具体实施过程和讲解方法。
四、六位一体教学方法
“二分法”是一元函数方程近似解法中最基础的一种方法,也是讲解后续内容的基础和对比对象。该教学内容要求学生了解求根问题的基本原理,熟悉求根问题策略选择,掌握二分法的算法步骤,熟悉二分法的收敛准则和使用方法。其中,重点要求学生掌握其算法步骤和程序设计方法,难点则是问题的收敛准则推导及对比。
(一)抛——激发兴趣
《购物街》是一套大众娱乐节目,深受大众喜爱。为此,教学中从《购物街》实例出发,让学生分别扮演主持人和观众角色,现场模拟竞猜“微波炉”价格,引出竞猜价格这一问题,模拟完毕后老师对该问题进行分析,将价格竞猜转化为数学问题,进而引出“根”“隔根区间”的概念。以轻松的游戏方式,打消了学生对课程难的顾虑,激发了学生的学习兴趣,活跃了课堂氛围。
(二)析——讨论辨析
将竞猜价格策略分为:A. 依据经验估计价格,并实时调整;B. 每次猜中间数;C. 依据偏好方向选择黄金分割点;D. 通过现场互动实时调整。教师课前通过微信群投票软件将上述策略发到课程群里,让全体学生参与投票,课堂上引导学生对问题进行讨论,辨析各种猜测策略的优劣所在,继而引出“二分法”常用策略的分类,即按有无先验信息分为两大类。
(三)探——探索比较
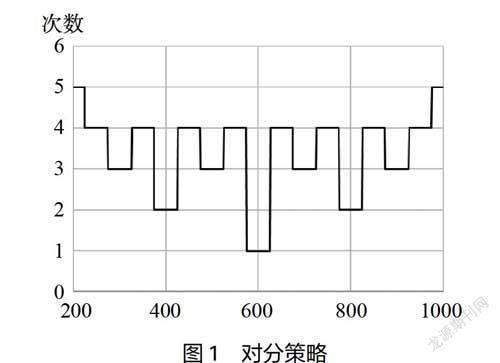
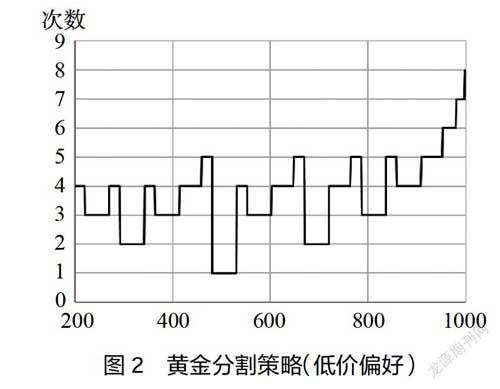
针对策略中无先验信息的分类情况,教师组织学生从最少次数、最多次数和平均次数三个方面,探索比较对分策略和黄金分割策略,从中得出一些基本规律,最终体现出对分策略的优势,由此顺利引出“二分法”的概念。如此,学生不仅掌握了基本概念,还了解了其在生活中的应用。
(四)炼——提炼步骤[10]
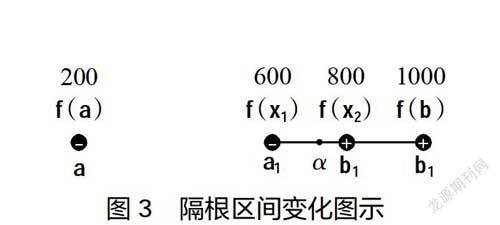
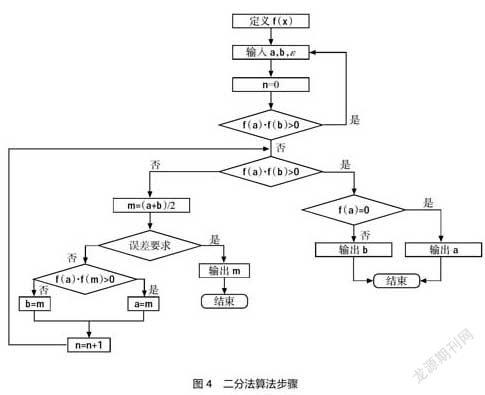
基于前面的竞猜游戏环节,教师启发学生深入分析二分法的算法步骤。再现竞猜情景,但此次对所猜价格给出“高了”“低了”的提示信息,对照之前“隔根区间”的划分概念,从中提炼二分法的算法步骤,并给出误差要求的概念。将隔根区间变化规律图示化,并将二分法算法步骤用流程图显示,从而解决学生“怵公式”的问题,使其在感性上认知并掌握二分法的算法步骤。
(五)解——演示总结
二分法的收敛准则是学生需要熟练掌握的教学内容之一,但其抽象难以理解。教师可以根据不同类型的数学函数,利用线图演示的方式,引导学生一起讨论“二分法”对于各类函数的适应性。在此基础上,总结出“二分法”的收敛条件,期间避免了烦琐的公式推导过程,并解决了学生“怵推导”的问题。
(六)拓——反面启发
为了学生能够掌握二分法的应用,教师在课堂上除讲解纯理论应用题之外,需列举日常生活实例进行拓展,如高压直流输电系统的可靠性评估、多雷达信号分选、装备故障快速诊断等等。除此之外,还采用反面启发的方式,给出不适合使用二分法求解的问题,如:有九枚金币中存在一枚假币(比真币轻),怎样利用天平找出假币?引导学生利用所学知识进行分析探讨,最后得出采用三分法求解要比二分法更快。熟知算法的应用是课程的核心,列举经典例题、生活实例以及专业问题,并采用正反实例结合比较的方式,可以让学生全方位理解和掌握算法,从而有效地解决学生“怵应用”的问题。
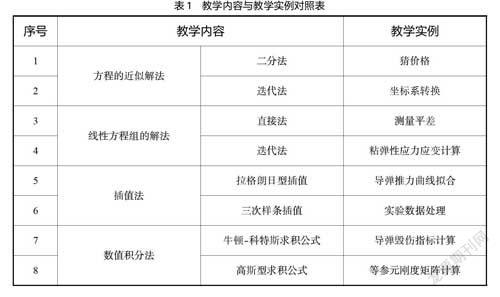
教师采用“抛-析-探-炼-解-拓”六位一体的教学方法,带领学生一起将“二分法”进行透彻剖析,显著提高了授课质量,同时也让学生体会了提出问题、分析问题和解决问题的基本过程,极大地鼓舞了他们的学习兴趣和自信心。对于计算方法课程,该方法还可以用于方程的近似解法、插值法、数值积分等章节的教学内容,具有一定的通用性,各算法的具体教学实例如表1所示。
表1 教学内容与教学实例对照表
五、小结
计算方法课程知识抽象,理论实践并重,难讲亦难学,本文提出的“抛-析-探-炼-解-拓”六位一体教学方法,按照对事物的认知规律,对各类算法进行逐步分析和深层凝练,可以有效地解决各类算法讲解过程中存在的难点问题。同时,教师在授课过程中引导学生亲身体验不同算法求解同一问题或同一算法求解不同问题的区别,促进学生掌握知识的同时,培养了学生循序渐进、举一反三的科学研究精神。该方法在进行授课实践的过程中,学生反馈效果较好,学习成绩显著提高,同时也得到了学校专家的一致认可。
参考文献:
[1] 汪海鹰,易发胜,张君雁. “数值计算方法”课程教学探索——以软件工程专业为例[J]. 教育与教学研究,2017,31(02):111-114+129.
[2] 张建华. 应用型人才培养中数值计算方法课程教学改革与实践[J]. 大学教育,2013(08):51-52.
[3] 孙国芹,刘小冬,许东来. 机械工程专业计算方法课程教学改革与实践[J]. 教育教学论坛,2020(09):121-122.
[4] 王班,周传平,周茂瑛. 《数值计算方法》课程教学改革探索[J]. 教育教学论坛,2020(08):222-223.
[5] 陈丽娟,李明珠,张蕾,等. 新工科背景下计算方法课程实践——融入数学建模思想[J]. 高教学刊,2020(18):74-76.
[6] 张国勇,毛欲民. 计算方法课程教学中计算思维培养研究[J]. 湖北师范大学学报(自然科学版),2018,38(04):98-102.
[7] 赵丽萍,舒期梁. 关于《数值计算方法》课程教学改革的探讨[J]. 办公自动化,2018,23(15):37-38+36.
[8] 耿爱成,史书慧. 工程硕士课程“数值分析”教学改革研究[J]. 沈阳师范大学学报(自然科学版),2017,35(04):494-497.
[9] 胡双年,马戈. 基于程序设计的计算方法课程教学改革与实践[J]. 高教学刊,2018(13):76-77+82.
[10] 黃晓林,陈嘉艳,徐骏. 以《计算方法》为例的经典课程课堂教学改革探索与实践[J]. 教育教学论坛,2019(16):136-138.
(责任编辑:汪旦旦)
