巧设数学习题 培养高阶思维

蒋梅

摘  要：在基础知识学习阶段，通过不同类型数学课习题问题设计，引导学生学习;在中考综合复习阶段，通过让学生从解答习题到改编习题，开启创新学习. 在完成教师设计的习题问题过程中，学生实现了从解题到编题的进阶训练，学生的分析与综合、评价、创造性思维能力得到训练，培养了高阶思维.

关键词：习题改编;创新学习;高阶思维

发展思维是数学教学过程中能力培养的核心. 培养学生的高阶思维，提升学生的能力是数学教学的主要任务. 精心设计习题，是培养学生高阶思维的重要途径之一. 高水平提问的基本点包括：反映当前学习内容的本质;在学生思维的最近发展区内，对学生思维形成挑战性;具有可发展性，形成系列问题;具有可模仿性，实现从“问题引导学习，激发学生思维”到“学生自主提问，展开创新学习”的过渡.

通过精心设计习题问题，可以让学生在习题的解答过程中产生较高认知水平的心智活动或较高层次的认知能力. 本文按照不同阶段数学习题承载的任务，进行分阶段的习题问题设计，力求培养学生的高阶思维. 主要分为在基础知识学习阶段，以习题问题设计引导学生学习;在中考综合复习阶段，以改编习题的方式开启创新学习.

一、巧设习题问题，引导学生学习

在基础知识学习阶段，教师可以根据不同类型的知识内容，设计不同层次的习题，聚焦当前学习内容的本质，以学生思维的最近发展区为出发点，对学生的思维形成一定的挑战性，这是培养学生高阶思维的基础.

1. 在新授课教学中，习题问题指向近阶段的相关学习内容

在正方形的新授课中，为巩固正方形的性质，把正方形的性质融入学生已有的知识体系中，设计了如下题目.

题目1  在边长为2的正方形ABCD中，

（1）求对角线AC的长.

（2）如图1，若BE平分∠DBC，交边AC于点F，求∠ABF的度数和CF的长.

（3）在（2）的条件下，延长BC至点G，使BG = BD，连接DG，延长BE交DG于点H. 求证：BE = DG.

以上题目从巩固正方形的对角线与边长的关系，到利用对角线平分对角这一性质，联系已有的“等角对等边”知识，把正方形的邻边相等、四个角都是直角等性质与等腰三角形“三线合一”、三角形全等知识相融合，将正方形的性质融入学生已有的知识体系中. 问题设计既指向正方形的性质，又把正方形的性质与学生已有的三角形相关的知识联系起来.

2. 在章节复习教学中，习题问题要有综合性和思维挑战性

在章节复习课中，需要对已学的知识进行整理，可以以习题为载体提升学生分析问题和解决问题的能力. 习题问题设计既要有知识的综合性，也要对学生的思维形成一定的挑战性.

在四边形的章末习题课中，笔者设计了如下一道题目.

题目2  如图2，在正方形ABCD中，E是边AB上的一个动点（不与点A，B重合），连接DE，G是边BC上一点，连接EG.

（1）若∠EDG = 45°，点F在线段EG上，且是点A关于直线DE的对称点，求证：GF = GC.

（2）若EG = AE + CG，求证：∠EDG = 45°.

（3）过点E作EH⊥DE，交DG的延长线于点H，连接BH，用等式表示线段BH与AE的数量关系，并证明.

第（1）小题需要利用正方形的邻边相等，融合轴对称的性质和三角形全等的知识来解决，在知识方面有一定的综合性;第（2）小题是把第（1）小题的条件与结论进行了互换，让学生能学会逆向思考，拓展思维;第（3）小题综合应用正方形与等腰直角三角形的性质，是一个结论未知的开放性问题，对学生的思维具有挑战性.

3. 在阶段综合复习教学中，可设计系列习题问题

这里的阶段综合复习，是指学期的期末考试复习. 习题设计可以以一个基础题为背景，在此基础上不断挖掘可以得到的系列结论.

题目3  如图3，正方形ABCD中，AC是对角线，点E是边BC上一点，连接AE，点E关于AB的对称点为点F，过点F作FG⊥AE，垂足为点H，交AC于点G.

（1）若∠BAE = α，用含α的式子表示出∠AGF的大小;

（2）求证：AE = FG;

（3）线段CG与BE存在怎样的数量关系？

此题将正方形的对角线平分对角、三角形的内角和与外角和的关系进行融合. 在此基础上，联系等腰三角形的性质与判定，再融入三角形全等和等腰直角三角形的边角关系，形成一道开放性的问题. 这三道小题，前一个问题为后一个问题做了提示、铺垫，问题向开放性发展，综合性逐渐增加，思维难度逐渐增大，形成了系列问题.

二、从模仿到改编，开启创新学习

在中考综合复习阶段，教师要设计可以帮助学生梳理知识体系、渗透开放性的习题问题，实现从“问题引导学习，激发学生思维”到“学生自主提问，展开创新学习”的过渡. 以下以四边形综合题专题复习为例，说明如何用问题引领学生从梳理知识体系到改编试题.

1. 问题导向，分析核心要素

学生通过习题中的问题引导，完成对知识的回顾与梳理，加深理解，建立所有知识信息之间的联系，自主建构知识结构体系.

在进行四边形专题复习时，教师可以设计以下的题目.

题目4  如图4，正方形ABCD中，AC是对角线，点E是边BC上一点，点F是CB延长线上一点，且BE = BF，连接AE，AF，过点F作FH⊥AE于点H，延长FH交AC于點G.

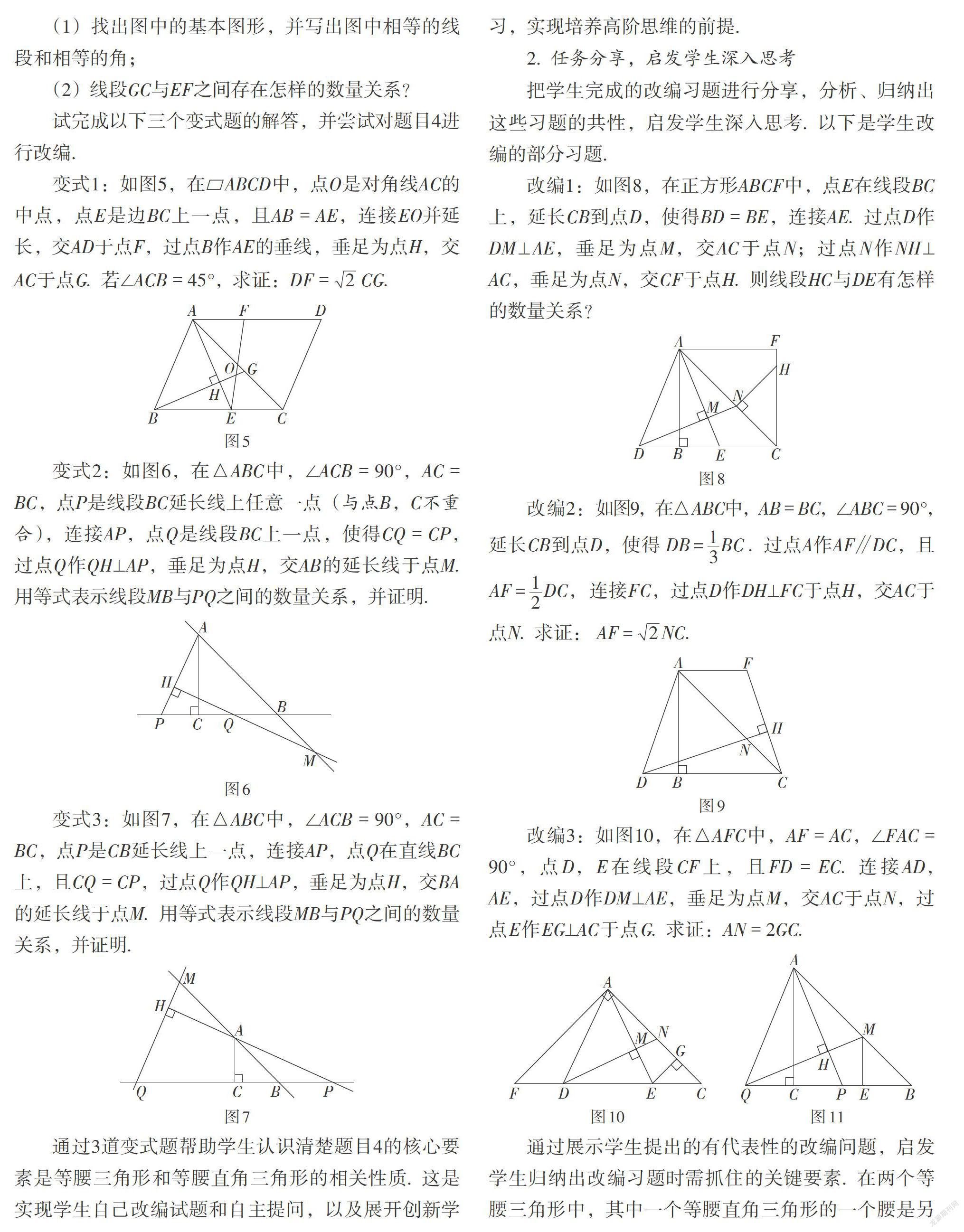
（1）找出图中的基本图形，并写出图中相等的线段和相等的角;

（2）线段GC与EF之间存在怎样的数量关系？

试完成以下三个变式题的解答，并尝试对题目4进行改编.

变式1：如图5，在▱ABCD中，点O是对角线AC的中点，点E是边BC上一点，且AB = AE，连接EO并延长，交AD于点F，过点B作AE的垂线，垂足为点H，交AC于点G. 若∠ACB = 45°，求证：DF =[2]CG.

变式2：如图6，在△ABC中，∠ACB = 90°，AC = BC，点P是线段BC延长线上任意一点（与点B，C不重合），连接AP，点Q是线段BC上一点，使得CQ = CP，过点Q作QH⊥AP，垂足为点H，交AB的延长线于点M. 用等式表示线段MB与PQ之间的数量关系，并证明.

变式3：如图7，在△ABC中，∠ACB = 90°，AC = BC，点P是CB延长线上一点，连接AP，点Q在直线BC上，且CQ = CP，过点Q作QH⊥AP，垂足为点H，交BA的延长线于点M. 用等式表示线段MB与PQ之间的数量关系，并证明.

通过3道变式题帮助学生认识清楚题目4的核心要素是等腰三角形和等腰直角三角形的相关性质. 这是实现学生自己改编试题和自主提问，以及展开创新学习，实现培养高阶思维的前提.

2. 任务分享，启发学生深入思考

把学生完成的改编习题进行分享，分析、归纳出这些习题的共性，启发学生深入思考. 以下是学生改编的部分习题.

改编1：如图8，在正方形ABCF中，点E在线段BC上，延长CB到点D，使得BD = BE，连接AE. 过点D作DM⊥AE，垂足为点M，交AC于点N;过点N作NH⊥AC，垂足为点N，交CF于点H. 则线段HC与DE有怎样的数量关系？

改编2：如图9，在△ABC中，AB = BC，∠ABC = 90°，延长CB到点D，使得[DB=13BC]. 过点A作AF∥DC，且[AF=12DC，] 连接FC，过点D作DH⊥FC于点H，交AC于点N. 求证：[AF=2NC.]

改编3：如图10，在△AFC中，AF = AC，∠FAC = 90°，点D，E在线段CF上，且FD = EC. 连接AD，AE，过点D作DM⊥AE，垂足为点M，交AC于点N，过点E作EG⊥AC于点G. 求证：AN = 2GC.

通过展示学生提出的有代表性的改编问题，启发学生归纳出改编习题时需抓住的关键要素. 在两个等腰三角形中，其中一个等腰直角三角形的一个腰是另一个非等腰三角形底边上的高，如图11所示，等腰直角三角形ABC的直角边AC也是等腰三角形APQ底边PQ上的高. 改编时，根据需要，可以适当隐去部分线段. 这样改编的题目的共同特点就是构造三角形全等，利用等腰直角三角形的边的关系解决问题. 这为学生改编试题提供了思考的方向，是实现培养高阶思维的路径之一.

3. 再度出发，归纳问题本质

欣赏同伴改编的试题后，再次引导学生思考：如图11，能否抓住△AQM与△APQ有公共腰AQ，且这两个等腰三角形的底边QP与AM所在直线相交成的角为45°这两个关键元素进行改编呢？这个能否成为改编的核心要素呢？经过思考，得到以下改编试题.

（1）如果两个等腰三角形有一腰重合，且顶角的顶点也重合.

改编1：如图12，在△ABC和△ABD中，AB = AC = AD，∠DBC = 45°，AE⊥BD，垂足为点E，交BC的延长线于点F. 求证：[CF=2AE.]

改编2：如图13，在△ABC和△ABD中，AB = AC = AD，∠DBC = 45°，AE⊥BD，垂足为点E，延长EA交BC于点F. 求证：[CF=2AE.]

（2）如果两个等腰三角形有一腰重合，但顶角的顶点不相同，得到以下的改编试题.

改编3：如图14，在△ABC和△ACD中，AB = AC = CD，DA的延长线交BC于点E，且∠DEC = 45°. 求证：[AD=2BE.]

改编4：如图15，在△ABC和△ACD中，AB = AC = CD，AD与BC交于点E，∠DEC = 45°. 求证：[AD=2BE.]

通过对一道题从不同角度进行改编，训练学生思维的独创性. 让学生通过实际例子的分析，感受到改编试题需要抓住核心要素. 聚焦点不同，改编出的试题也各异. 由此可见，改编试题的思维路径是多样的.

改编试题时，学生需要先分析清楚原题的核心元素，找到可以变化的因素，并且需要找到变化后存在的正确结论，这个过程中会产生较高认知水平的心智活动.

三、从解题到编题，培养高阶思维能力

高阶思维能力是发生在较高认知水平层次上的心智活动或较高层次的认识能力，也是解决“劣构”性问题所必要的理性思维. 高阶思维能力包括分析、综合、评价和创造能力.

1. 设计好习题问题的内容，培养分析与综合的能力

在解题阶段，通过习题问题的设计，让学生自己建构、完善知识体系，这是一种思维的架构. 同时，在解答习题的过程中，让学生分析清楚已知条件和未知问题，思考由已知条件可以得到哪些结论，在增加什么条件下可以得到哪些新的结论，要得到这个结论需要什么条件，在这样的思考过程中提升分析与综合的思维能力.

2. 设计好习题问题的层次，培养评价能力

有层次性的习题问题可以帮助学生抓住习题中的核心和关键，把思维逐渐引向深入. 学生在习题问题的引导下，从直接应用到思考开放性问题，到自己改编试题，可以自己对试题的核心要素进行选择与保留，在与同伴交流的过程中，通过对同伴的解答做出评价，培养学生具备一定的评价能力.

3. 利用好生成的資源，培养创造性思维能力

从完成习题的解答，到改编习题，整个过程中，学生完成习题时存在的问题，是教师进一步改编和完善习题的基础. 学生改编的习题，是教师对学生思维能力与水平了解的一种方式，这些都是教学可用的生成性资源. 学生在改编习题的过程中，通过与同伴分享，相互启发，促进其深入思考，这是实现个性化创新的学习方式，是培养学生创造能力的一种重要方式.

通过对不同阶段数学教学习题的不同设计，启发学生从理解题意开始，从解题到模仿编题，分析、归纳改编试题的共性，认识到综合试题的核心要素，并进行个性化的试题改编，开启创新学习，让学生从做题到研究题，促使认知水平的心智活动或较高层次的认知能力发生，实现对学生高阶思维的培养.

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2]陈玉伦. 初中数学课堂培养高阶思维能力：以“分式方程”的教学为例[J]. 中学数学数学研究（下半月），2019（5）：22-23.

[3]张淑清. 挖掘真题价值  引领教学方向：以2017年北京市中考一道几何综合题为例谈几何教学[J]. 中国数学教育（初中版），2019（5）：49-52，57.