基于移动粒子半隐式方法波传播模型的声传播数值求解方法研究

周子棋,孙一颉,韩沛东,孙中国,席光

(西安交通大学能源与动力工程学院,710049,西安)

声传播可用波动方程[1]来表述,求解该方程的数值方法包括有限差分法、有限元法、谱元法和边界元法等[2]。这些方法须基于网格求解,对网格数量和质量较为敏感。无网格法消除了传统数值计算对于网格的依赖性,典型的无网格方法有无单元伽辽金法、杂交边界点法、径向基函数法、光滑粒子动力学方法、移动粒子半隐式法等[3],其中径向基函数配点法求解椭圆型、抛物型和双曲型微分方程获得了广泛应用[4]。该类方法具有不用网格剖分、无需积分运算的特点,但其多基于欧拉描述,不易于应用到计算域随时间变化的非定常问题,因此采用无网格粒子方法建立声传播的计算模型较为可行。Hahn对光滑粒子动力学方法计算声传播问题时的计算参数和边界条件设置进行了讨论[5]。魏建国等对比了光滑粒子动力学与时域有限差分方法的计算结果,验证了其正确性[6]。张咏鸥等在一系列论文中逐步完善了声传播模型在光滑粒子动力学中的表达形式和相关边界条件[7-9]。

移动粒子半隐式法(MPS)[10]是一种较新的无网格粒子方法,适合用于求解带有大变形、自由面、移动边界等复杂非定常问题。在MPS方法中,声传播模型尚未提出,为了建立基于MPS的声波传播模拟方法,本文从流声分离假设[1]出发,推导了声传播控制方程,实现了典型边界条件,研究了CFL数及粒子间距等关键参数对计算精度的影响,并通过数值计算算例进行了验证。

1 数值方法

1.1 控制方程

MPS方法中,不可压缩流动下的质量守恒方程与动量守恒方程为

(1)

(2)

式中:ρ为流体密度;u为流体速度;p为压力;μ为动力黏度;f为体积力。

1.2 核函数和离散算子

核函数描述了粒子之间的作用关系,需要满足紧支性条件[11],本文采用的经典核函数及离散算子如下

(3)

(4)

(5)

式中:w(r)为核函数;r=|ri-rj|为i、j粒子之间距离;re一般取2.1l0;φ是任意标量函数;d为维度;n0是粒子数密度常数。在忽略连续域内核函数截断误差的情况下,拉普拉斯算子可简化为

(6)

(7)

2 声学计算模型

本文构建的声学计算模型称为MPS-WP模型,包括声学控制方程的粒子离散表达方程组、经典四阶Runge-Kutta时间积分法[12]和典型边界条件模型。MPS-WP模型应用了MPS方法中的离散算子和粒子表达形式,可在MPS方法求解得到的流场信息的基础上计算声场信息,扩大了MPS方法的应用范围。

2.1 声学控制方程及方程离散

声波传播的介质多为空气或水等黏性及导热系数均较小的流体,其扰动的空间梯度相比扰动本身较小,因此黏性和热传导的影响可以忽略不计,扰动的传播可以通过求解欧拉方程、连续方程和声速方程来确定。其中,连续性方程为

(8)

欧拉(动量)方程为

(9)

声速方程为

(10)

假设流体为单一组分且热力学平衡,对于定常流,在没有外力或质量增加的条件下,方程(8)～(10)可以改写为方程组

(11)

方程组(11)描述了某一扰动在流体中的传播过程。声场的基本物理量可表示为流场物理量上叠加的微小扰动,其关系表示为

(12)

方程组(11)可以改写为

(13)

(14)

(15)

方程(13)～(15)定义了流声分离假设下声学物理量在声传播过程中的随体导数表达式。本文计算环境为不可压缩静止无黏流场,上式可简化为

(16)

(17)

(18)

方程离散后可得到3个声学物理量的导数表达式,对于声波来说,通常为纵波,其扰动速度在x和y方向存在分量δu和δv。式(16)～(18)可写为

ri)w(|rj-ri|)

(19)

xi)w(|rj-ri|)

(20)

yi)w(|rj-ri|)

(21)

ri)w(|rj-ri|)

(22)

即MPS-WP在不可压缩静止无黏流场下的表达形式。如需计算横波,即振动方向与传播方向垂直的波,在二维条件下则仅需要一个扰动速度分量,其具体表达式与式(19)～(22)类似,本文不再赘述。

2.2 时间积分方法

时间积分采用经典四阶Runge-Kutta法,替代MPS常用的一阶欧拉法yn+1=yn+hf(tn,yn),以保证其在声波传播计算中的高精度及收敛性。四阶Runge-Kutta时间积分方程为

(23)

式中:f(tn,yn)为物理量yn在tn时刻的导数;h为虚拟时间步长。

2.3 边界条件模拟

粒子方法常采用虚拟粒子来解决支持域截断问题,在声学计算中,虚拟粒子也可用于表征声学边界条件。对于声学硬边界,即在壁面处满足条件

(24)

采用虚拟粒子在边界处镜像内部粒子得到

δp(i+1)=δp(i);δv(i+1)=0

(25)

对于吸收边界,本文采用在FDTD中广泛使用的Mur边界[13]进行粒子离散表达,如图1所示。

图1 右侧边界粒子布置示意图Fig.1 Boundary particles arrangement on right side

对于边界条件粒子,满足如下方程

(fn(i,j)-fn-1(i+1,j))

(26)

(fn(i,j)-fn-1(i+2,j))

(27)

2.4 计算参数选取

模型计算精度受粒子间距l0和CFL数的影响。定义CFL数为

(28)

式中:c0为声波传播的速度;dt为实际时间步长;l0为粒子间距。

针对100 m×100 m方形计算域中的高斯脉冲传播过程模拟,当l0=0.5 m时,CFL数与声压的相对均方根误差关系如图2所示。当CFL数小于0.68时,不同时刻的计算误差均较小。

图2 不同CFL数下的相对均方根误差Fig.2 Relative root mean square error at different CFL numbers

当CFL数为0.17时,粒子间距与声压的相对均方根误差关系如图3所示。当l0小于0.5 m时,不同时刻的计算误差均较小。在本文的计算中,取CFL数为0.136,l0=0.25 m。

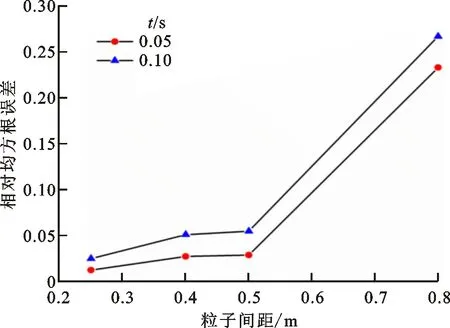
图3 不同粒子间距下的相对均方根误差Fig.3 Relative root mean square error at different particle spacings

3 结果与分析

3.1 二维高斯脉冲传播

参考NASA标准算例[14]建立二维高斯脉冲计算。初始时刻声压分布为

(29)

任意时刻的声压解析解可以表示为

(30)

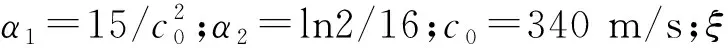
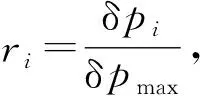
(a)t=0 s

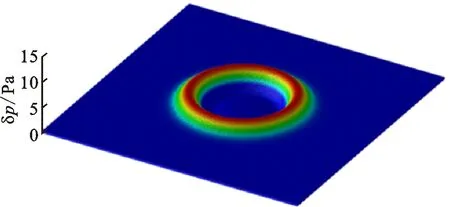
(b)t=0.05 s

(c)t=0.10 s图4 二维高斯脉冲传播的声压分布Fig.4 Acoustic pressure distributions in two-dimensional Gauss pulse propagation

图5为采用MPS-WP在中心位置沿x方向提取得到的声压分布以及与解析解的对比,结果表明MPS-WP的计算结果与解析解吻合较好。

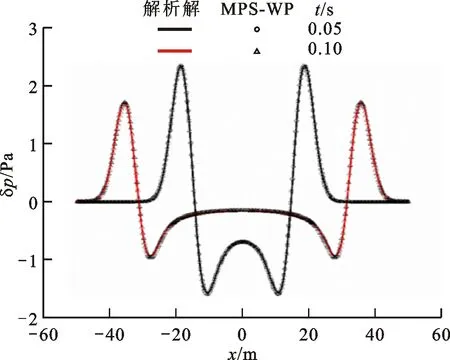
图5 中心位置处沿x方向的声压分布Fig.5 Acoustic pressure distributions at center along x-direction

3.2 硬边界条件下的高斯脉冲传播

(a)t=0.1 s

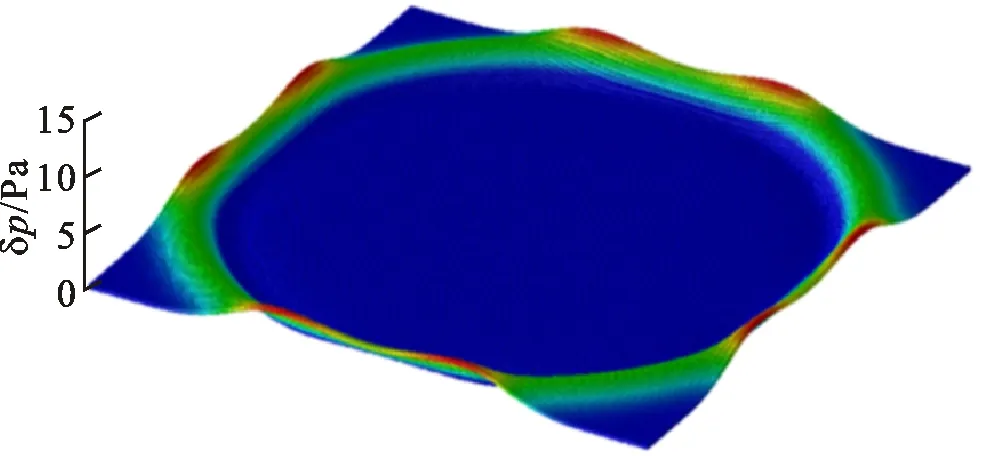
(b)t=0.15 s

(c)t=0.20 s图6 声学硬边界条件下高斯脉冲传播的声压分布Fig.6 Acoustic pressure distributions of Gaussian pulse propagation under acoustic hard boundary condition

声学硬边界表现为声波在壁面处的全反射。基于式(25)施加了声学硬边界。高斯脉冲的传播情况如图6所示。由图6可知,在0.15～0.20 s间,脉冲与壁面接触产生反射和叠加。y=0处的声压分布如图7所示,在声学硬边界条件下,计算结果与解析解吻合良好。

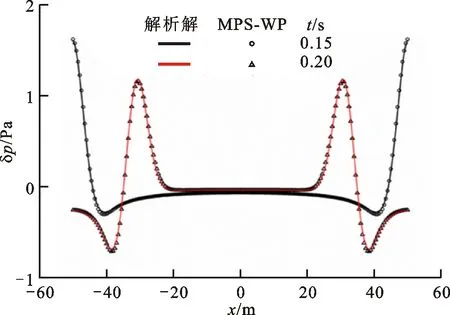
图7 声学硬边界条件下声压的MPS-WP计算解与解析解的对比Fig.7 Acoustic pressure comparison under hard boundary condition between the MPS-WP solution and the analytical solution

3.3 吸收边界条件下的高斯脉冲传播

声场计算中,通常采用吸收边界来减小反射波,以消除人工截断边界对于计算域的影响。图8为在Mur吸收边界条件下的高斯脉冲传播。在0.15～0.20 s时,声波在边界处完全消失,无明显反射波存在。

(a)t=0.1 s

(b)t=0.15 s

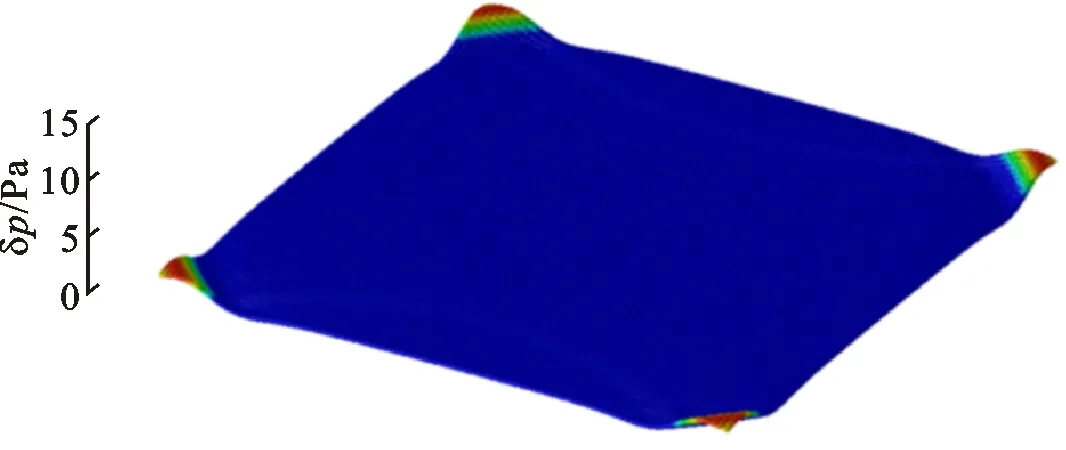
(c)t=0.20 s图8 Mur吸收边界条件下高斯脉冲传播的声压分布Fig.8 Acoustic pressure distributions in propagation of Gauss pulse under Mur absorbing boundary condition

同样地,提取在y=0处的声压分布(见图9),可以看到0.15 s时MPS-WP在Mur吸收边界条件下的计算结果和解析解吻合良好。

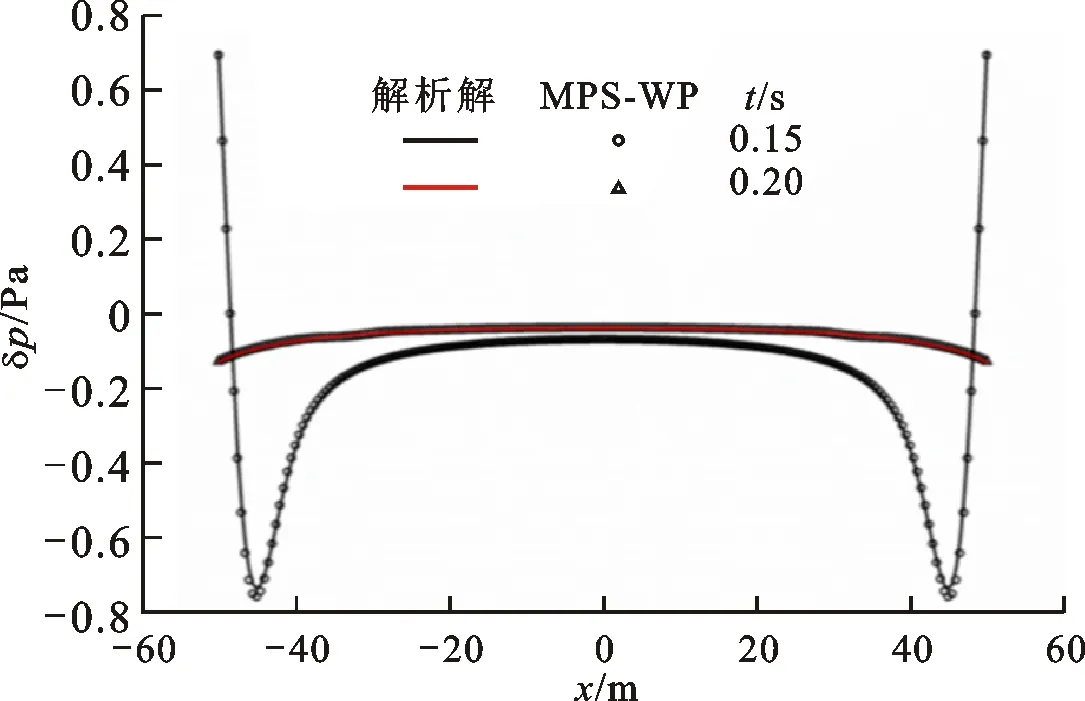
图9 Mur吸收边界条件下声压的MPS-WP计算解与解析解的对比Fig.9 Acoustic pressure comparison under Mur absorbing boundary condition between the MPS-WP solution and the analytical solution

3.4 两高斯脉冲叠加

(a)t=0 s

(b)t=0.05 s

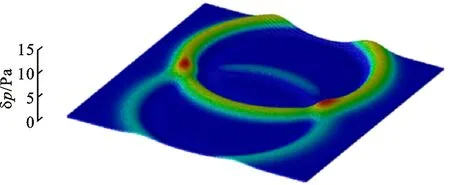
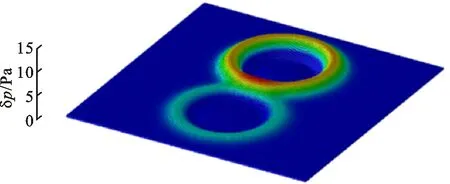
(c)t=0.10 s图10 两高斯脉冲传播的声压分布Fig.10 Acoustic pressure distributions in propagation of two Gauss pulses

图10为不同时间点声压分布的情况,可知脉冲在计算域内的传播情况较好。在t=0.05 s时两脉冲边缘接触,出现了声压幅值的叠加;在t=0.10 s时,交点位置因为声压叠加达到最高值,脉冲向前传播后抵达吸收边界。

同样地,采用MPS-WP提取y=0位置的声压分布与解析解对比,如图11所示,采用MPS-WP计算的声压分布与解析解吻合较好。

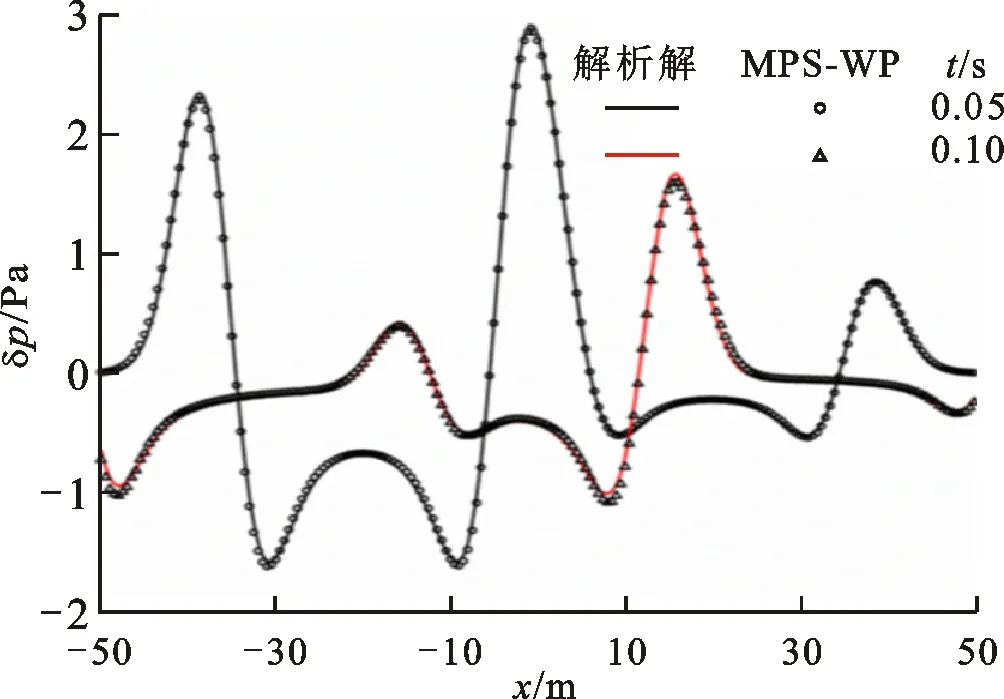
图11 两高斯脉冲传播声压的MPS-WP计算解与解析解的对比Fig.11 Acoustic pressure comparison in propagation of two Gauss pulses between the MPS-WP solution and the analytical solution

3.5 流动条件下的声波传播

脉冲声源在运动流体中传播存在多普勒效应。对于均匀流动下的声传播问题,有

p0=0;·v0=0

(31)

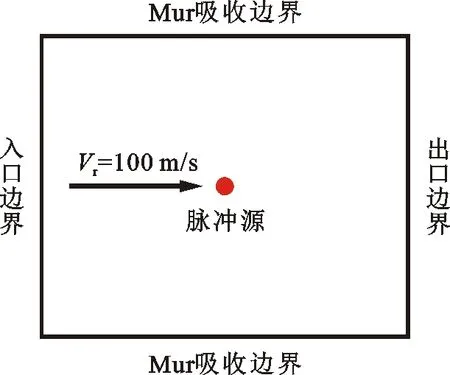
图12 均匀流动下声场传播计算域布置Fig.12 Computational domain arrangement of acoustic wave propagation in uniform flow

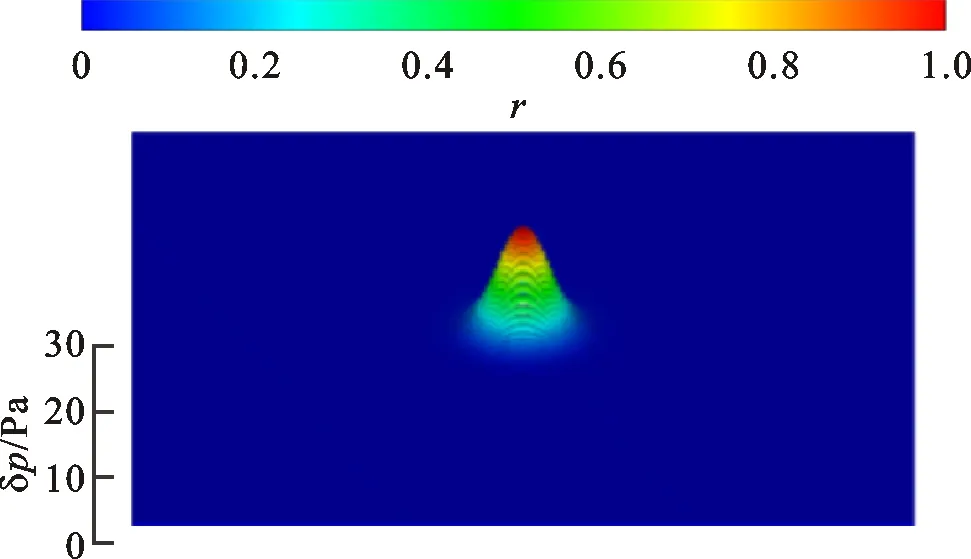
(a)t=0 s

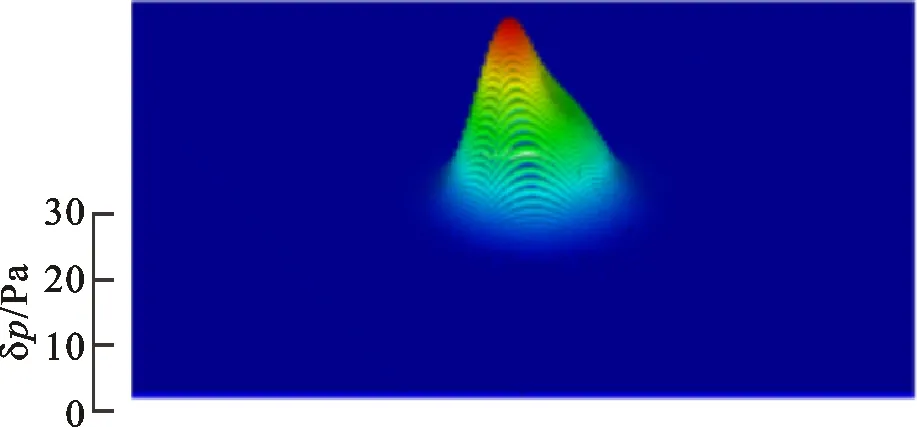
(b)t=0.01 s

(c)t=0.02 s

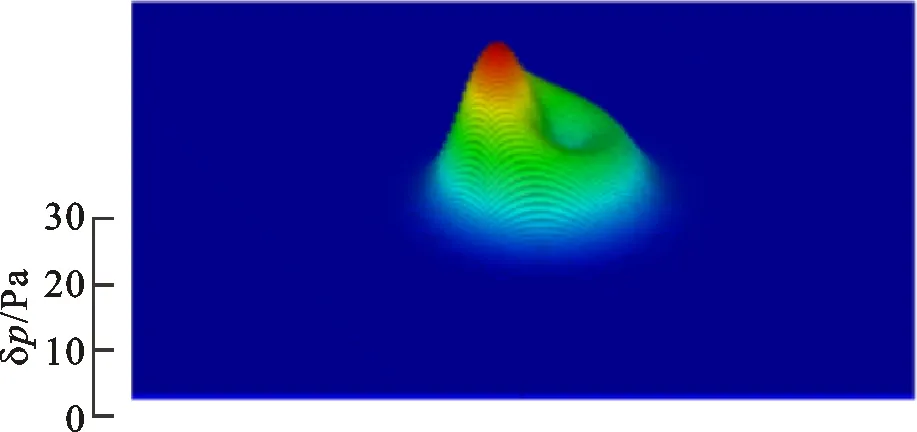
(d)t=0.03 s图13 均匀流动下多脉冲传播的声压分布Fig.13 Acoustic pressure distributions in propagation of multiple Gauss pulses in uniform flow

则依然满足方程(13)～(15)、(16)～(18)的简化过程,故可以将该模型拓展到均匀流动的声传播计算中。算例中高斯脉冲位于方腔中心,方腔上下边界为Mur吸收边界,左右分别为入口和出口边界;对于流动,进出口分别为均匀速度进口以及出口边界,两侧壁面为完全滑移边界,壁面对流动不产生影响,则整个流场的均匀性保持不变。在均匀流动中速度Vr=100 m/s,高斯脉冲的产生频率为200 Hz,其余参数与上文设置相同,如图12所示。计算结果如图13所示,随着时间推进,声压在脉冲源的均匀来流方向叠加,脉冲在下游方向的传播距离较上游方向远。t=0.02s时多次脉冲叠加的结果如图14所示,计算结果与解析解一致。

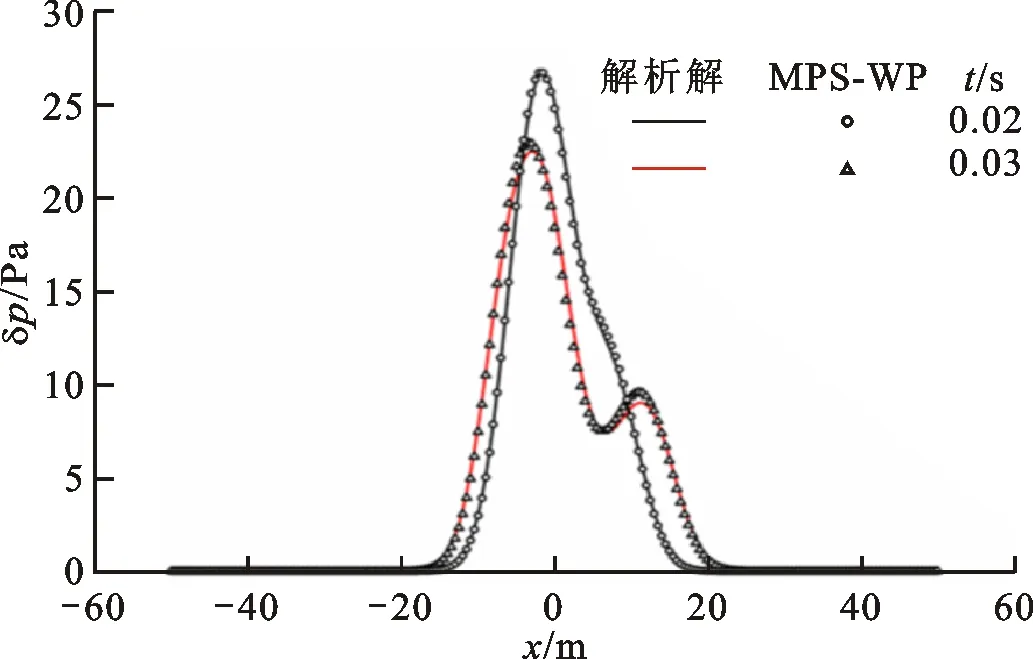
图14 均匀来流条件下声压的MPS-WP计算解与解析解的对比Fig.14 Comparison of acoustic pressure distributions in uniform flow between the MPS-WP solution and the analytical solution

4 结 论

本文基于无网格MPS粒子方法,在拉格朗日框架下建立了用于计算声传播问题的计算模型MPS-WP,实现了硬边界和Mur吸收边界两类边界条件的离散表达。在本文的算例中,研究了CFL数和粒子间距对计算结果的影响并确定了适用范围,模拟了二维高斯脉冲在硬边界和Mur吸收边界下的传播过程,验证了模型和边界条件的正确性。本文还对静场中脉冲叠加及均匀来流条件下的连续脉冲传播过程进行了数值模拟和研究,计算结果与解析解吻合良好,为在复杂流场计算声传播问题提供了一种有效途径。