抗单粒子瞬态的辐射加固压控延时单元

史柱,赵雁鹏,高利军,杨博,王斌,刘文平

(西安微电子技术研究所,710065,西安)

随着集成电路和空间技术的不断发展,面向空间应用的大规模集成电路中已经集成了处理器、存储器和通信系统,这些系统的接口电路中分布着大量的时钟网络,控制数据传输的时序[1]。由于输出时钟精度高、电路设计简单,在不需要频率变化和时钟综合的应用中,电路设计者往往倾向使用延迟锁相环(DLL)[2-3]。研究表明,在辐射环境中,压控延迟线是延迟锁相环中对单粒子事件最敏感的子电路之一[4-5],该模块产生的单粒子瞬态(SET)会使得时钟信号发生错误翻转,造成整个系统功能的紊乱。

压控延时单元是组成压控延迟线的基本单元,一条宽调节范围的压控延迟线是由许多基本的压控延时单元串接而成。由于所占面积大,敏感节点数多,因此对压控延迟线加固的关键在于如何提高基本的压控延时单元的抗辐射性能[6-8]。文献[9]对基本的延时单元做了冗余备份,然后通过组合逻辑电路,滤除了受到单粒子轰击的输出信号,从而起到了加固效果,但是每个单元都做备份使得压控延迟线的面积增大了一倍,功耗也明显增加。文献[10]提出了交叉耦合负载结构(CCL)的延时单元,通过自身负载的反馈作用抑制节点电压的翻转。然而实际仿真可以看出,这种结构在入射粒子能量较低时就已经发生了明显的翻转。针对目前加固方法中的不足,本文提出了一种新型的加固压控延时单元。在延时单元输出节点之间,额外增加2个NMOS管和PMOS管,形成正反馈机制。该结构起到稳定输出节点电压的作用,同时只增加较少的面积。首先通过计算机辅助设计技术(TCAD)混合仿真验证了加固后的单个压控延时单元的抗单粒子瞬态效果,然后利用校准好的双指数电流源[11-12]通过Spice仿真验证了所提结构在工作状态下的延迟锁相环中的加固作用。

1 电路结构及加固原理

1.1 基本压控延时单元的敏感性分析

图1所示为延迟锁相环中的压控延迟线。输入参考时钟clkin经过缓冲级之后,分成两路差分模拟信号,同时经过双端转单端电路(D2S)生成clk时钟信号。每经过1/4总长度的延迟线,便通过同样的过程产生一路单相时钟,依次分别形成相位差为90°的四相时钟clk90,clk180,clk270和clk360。本文采用SMIC 45 nm工艺,相邻时钟之间有5级延时单元。在每一个延时单元的信号中,本级的输入信号Vin、Vip分别是上一级的输出信号;本级的输出Von、Vop又作为下一级的输入信号。

图1 延迟锁相环中的压控延迟线Fig.1 Voltage-controlled delay line in a DLL

图2为基本压控延时单元,该结构可看作电流源和二极管负载的单级运放[13-14]。控制电压VbN和VbP分别是NMOS管和PMOS管的偏置电压,VbN控制总的偏置电流;当输出电压Vop和Von相等时,两边支路电流ID相同,此时有

图2 基本压控延时单元Fig.2 Basic voltage-controlled delay cell

(1)

(2)

式中:μP是空穴迁移率;VTP是PMOS管的阈值电压;Cox是单位面积栅氧化层电容,因此延时单元的等效延迟时间为

(3)

式中:Cnode为节点电容,因此由(3)式可知,在延迟锁相环锁定过程中,通过不断调节控制电压VbN和VbP可以均匀调节每一个基本延时单元的延时大小。与此同时,锁定检测模块lock_det不断检测clko与clk360上升沿之间的时间差,当误差处于检测的范围内时,电路锁定。此时,压控延迟线中传输着时间间隔相等、高低电位交替的信号。该信号经过双端转单端电路便生成了占空比为50%的方波信号作为输出时钟。

延时单元中的信号,大部分时间是稳定的高低电平,可以用数字信号中的0和1来描述。当Vip=0,Vin=1时,由于N5管不导通,Von节点电容会被充至高电位,而Vop被N6管拉低,输出低电平。此时,如果有粒子轰击Von节点,会发生类似于反相器输出节点的单粒子瞬态现象[15]。因此Von节点电压将会从高翻转至低,如果翻转的幅度够大,使得Von低于Vop节点电压的持续时间足够长,则会造成D2S模块对电平识别错误,使得输出时钟发生错误翻转。由于延时单元的结构和功能完全对称,所以Vop的翻转情况和Von完全相同,这里不再赘述。对于Z节点,由于N7管控制整个电路的偏置电流,且N7、N6与P2、P4分压呈现出低电位,因此该管的尺寸远大于N5、N6,寄生电容大,受到SET脉冲电流产生的波动较小,因此Z节点的单粒子敏感性较弱。

1.2 基本延时单元的加固

根据前文中分析,当延迟锁相环处于稳定的锁定状态时,压控延迟线中的信号可以看作数字0和1。因此,基于数据锁存的思想,对这样稳定状态进行加固。本文提出了图3所示的加固的压控延时单元结构。通过增加4个晶体管P8、P9和N10、N11形成稳定的正反馈结构,实现加固。该电路的原理如下:当Von输出为1时,P9管不通而N11导通,加强了Vop为0的状态,同时Vop为0又使得P8导通,N10关闭,使得Von更加稳定。为了适应压控延迟线的宽调节范围,这里将N10、N11管的源极接到可调节的VbN节点,使得该4管组成的反馈结构的驱动能力随着锁定频率的不同而调节。除此之外,增加的管子使得每个输出节点都增加了两个栅电容Cg和两个漏结电容Cdj,也能起到稳定电压的作用。由于输出节点的状态主要由基本延时单元原来的管子决定,只有当输入发生跳变时状态才会翻转,且增加的管子尺寸相对较小。因此,即使增加的管子受到轰击,对输出影响也不大。

图3 加固的压控延时单元Fig.3 Radiation-hardened voltage-controlled delay cell

抗辐射加固设计是电路性能与可靠性之间的折中。根据式(3),提出的结构中增加的4个晶体管使得输出节点电容变为

(4)

单级延时的时间也相应增加为

(5)

延迟锁相环的频率与延时时间成反比,因此提出的结构是在降低了工作频率的前提下获得了抗单粒子性能。

2 单粒子敏感性仿真方法

为验证本文提出的延时单元加固效果,首先基于Sentaurus TCAD仿真平台对N5管构建三维器件模型,然后通过混合仿真的方式,模拟了加固前后的延时单元的单粒子瞬态响应。其次,本文对TCAD仿真中由粒子入射引起的SET脉冲电流与双指数电流模型[16]进行拟合。将拟合好的电流作为Spice仿真中的粒子入射条件,基于Cadence Spectre仿真工具,对延迟锁相环锁定状态下的延时单元加固效果与未加固单元作了对比。

图4中N5管是经过工艺校准的NMOS管三维器件模型。在混合仿真时,设置了高、低两种能量的粒子对N5管的漏极几何中心进行垂直入射,分别对应的入射粒子能量φ1为20 MeV·cm2/mg以及φ2为80 MeV·cm2/mg。通过Von节点的电压翻转情况来描述加固前后的延时单元对单粒子瞬态的响应。Spice仿真中采用双指数电流源作为粒子入射条件,该电流模型如下式

(6)

式中:I0表示双指数电流脉冲峰值;τr和τf分别为上升和下降时间常数。图5给出了在本文的电路尺寸、工作点以及工艺条件下,入射粒子能量为φ2时,双指数电流与TCAD混合仿真中的SET电流拟合结果I0=1.18 mA,τr=6 ps,τf=35 ps;而当入射粒子LET值φ1为20 MeV·cm2/mg时,拟合过程相同,其结果为I0=502 uA,τr=4 ps,τf=45 ps。

(a)基本延时单元

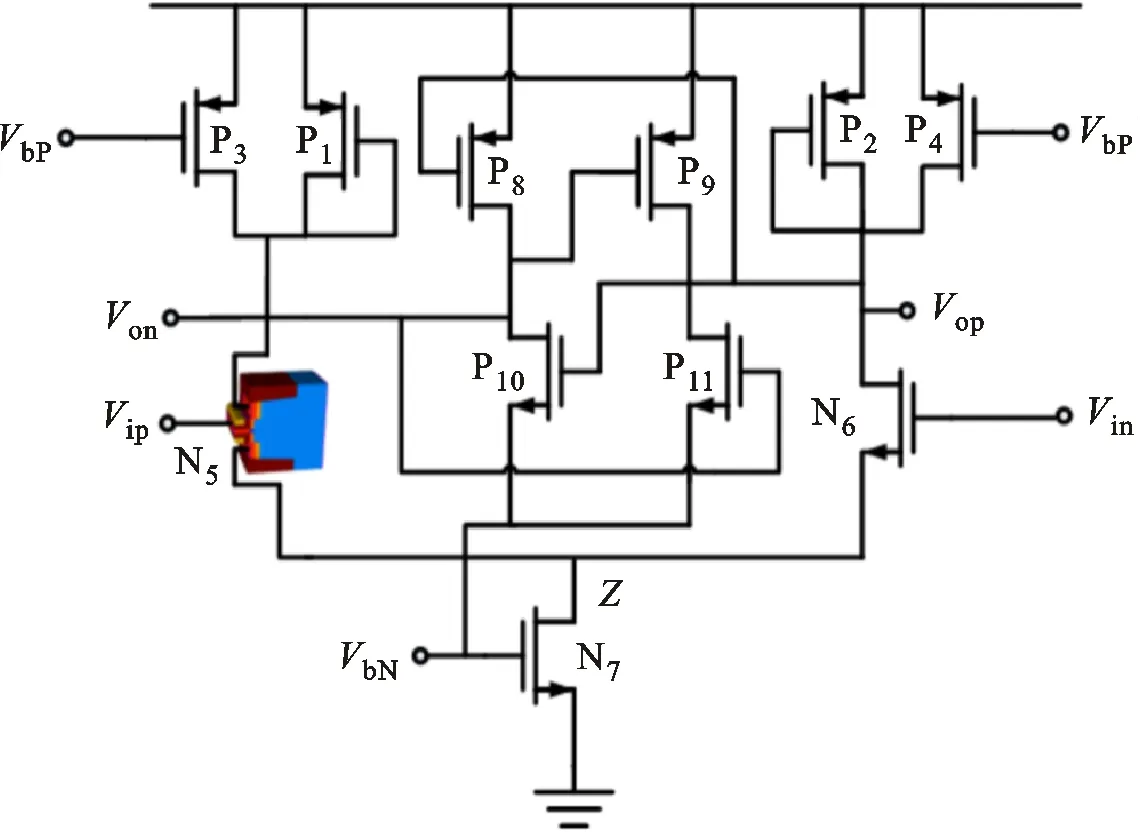
(b)加固的延时单元图4 3D TCAD混合仿真电路Fig.4 3D TCAD mixed-mode simulation circuit

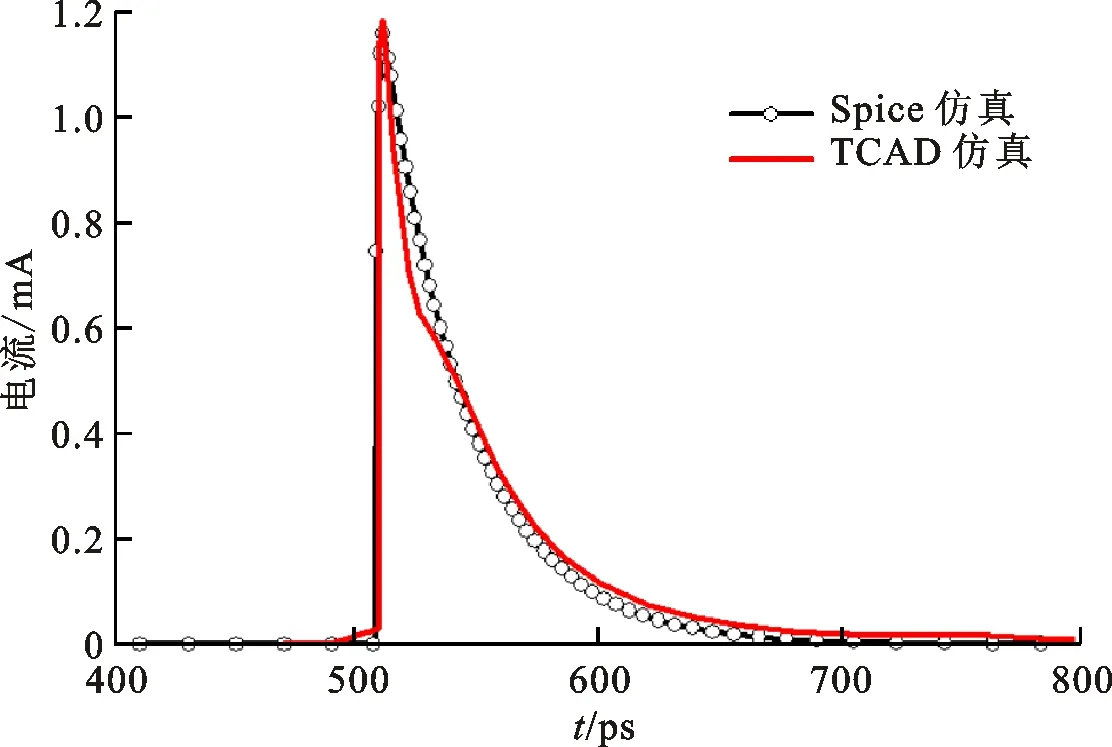
图5 双指数电流与TCAD仿真的SET电流校准结果Fig.5 Double exponential current calibrated to SET current from TCAD simulation

3 仿真结果及分析

(a)基本延时单元的常态仿真结果

(b)粒子入射基本延时单元Z节点的仿真结果图6 基本延时单元混合仿真图Fig.6 Simulation result of basic circuit in mixed-mode

在进行粒子入射之前,本文首先对搭建的混合仿真电路进行常态下工作状态仿真,结果如图6所示。从图6a中可以看出,输入为互补的正弦波,输出曲线光滑,波形周期均匀,具有比较理想的负载对称性。说明本文构建的N5器件三维模型能够合理取代Spice模型进行混合仿真实验。图6b中,采用能量φ2为80 MeV·cm2/mg的粒子垂直入射N5管的源极,即Z节点。结果显示,高低电平处,电位只是发生了轻微的扰动,但是并未改变上升和下降的趋势,对信号的周期几乎没有影响。因此可以认为,该节点对单粒子事件不敏感。

根据前文分析,当Von节点处于高电平时会产生单粒子瞬态,因此选取Von高电平中间时刻,对N5的漏极进行粒子轰击。本次仿真的LET值φ1为 20 MeV·cm2/mg,结果如图7所示。粒子轰击之后,基本延时单元的输出节点电压瞬间从电源电压1.1 V翻转至最低点-0.57 V,翻转幅度为1.67 V;与此同时,加固的延时单元最低电压为0.18 V,翻转幅度为0.92 V。加固之后,低能量粒子轰击的电压翻转幅度降低了44.9%。从图7中可以发现,在对加固后的延时单元进行TCAD混合仿真时,负载对称性稍微有所下降。该现象主要是由于实际电路中VbN接在下拉通路上,而混合仿真时只给出固定电位,与真实的工作环境稍有偏离,但是在后续的整体电路Spice仿真中,负载对称性良好。

(a)基本延时单元的单粒子瞬态

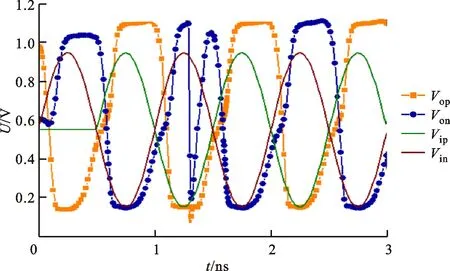
(b)加固的延时单元的单粒子瞬态图7 LET值为20 MeV·cm2/mg延时单元输出节点的单粒子瞬态Fig.7 SET in the output node of the voltage-controlled delay cell at 20 MeV·cm2/mg

图8给出了LET值为φ2时,加固前后的电压翻转幅度对比。从图8中可知,对于未加固单元,粒子入射之后,Von节点的电压很快从电源电压翻转至最低点的-0.95 V,翻转幅度达到了2.05 V;而加固的延时单元,其最低点所对的电压为-0.47 V,将翻转幅度降低了23.7%。在加固的延时单元中,虽然输出电压Von向下翻转的同时,Vop轻微向上跳变,但是由于Von已经远低于Vop,此时Vop节点电压是否向上翻转,识别出来的电平是一样的,对结果并未影响。尽管在高能量的粒子入射时,两个电路都发生了翻转,然而加固的结构还是降低了翻转的幅度,这样的降低在实际电路中一定程度上也起到了避免错误的效果。

(a)基本延时单元的单粒子瞬态

(b)加固的延时单元的单粒子瞬态图8 LET值为80 MeV·cm2/mg延时单元输出节点的单粒子瞬态Fig.8 SET in the output node of the voltage-controlled delay cell at 80 MeV·cm2/mg

为了进一步验证提出的加固延时单元的效果,本文对两种能量的粒子入射基本延时单元时产生的SET电流与双指数电流进行拟合。用拟合好的电流模拟Spice仿真时的粒子入射,对加固前后的延时单元在实际的延迟锁相环工作中的单粒子瞬态进行仿真,对比了加固效果。

如图9所示,在1 GHz的输入参考时钟频率下,延时锁相环锁定期间,对产生clk90时钟的延时单元进行粒子轰击,入射LET值φ1为20 MeV·cm2/mg。

图9a是未加固的延时单元受到轰击后,产生的时钟波形畸变。粒子入射导致圆圈中的时钟波形占空比发生变化,相邻时钟之间的相位关系也发生了变化。但在图9b中,经过加固之后的延时单元缓解了延时单元的翻转幅度,时钟波形正常输出。

(a)延迟锁相环中基本延时单元的单粒子瞬态

(b)延迟锁相环中加固的延时单元的单粒子瞬态图9 LET值为20 MeV·cm2/mg工作状态下的延迟锁相环中的单粒子瞬态Fig.9 SET in the voltage-controlled delay cell of a working DLL at 20 MeV·cm2/mg

图10给出了LET值φ2为80 MeV·cm2/mg时,锁定状态下的加固前后延时单元的单粒子瞬态响应,轰击的节点选择生成clk时钟的延时单元。图10a中显示,粒子轰击同样造成了时钟波形占空比变化,引发时序错误,而且这个错误被锁定检测模块检测出来,出现了一个周期的高脉冲;而加固之后的延时单元减缓了翻转的幅度,降低了错误电平维持的时间,使得D2S模块来不及响应,因此未形成时钟波形畸变,起到了加固的效果。

(a)延迟锁相环中基本延时单元的单粒子瞬态

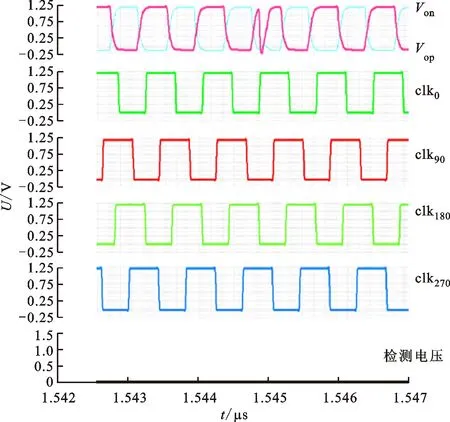
(b)延迟锁相环中加固的延时单元的单粒子瞬态图10 LET值为80 MeV·cm2/mg工作状态下的延迟锁相环中的单粒子瞬态Fig.10 SET in the voltage-controlled delay cell of a working DLL at 80 MeV·cm2/mg

根据上述结果,本文提出的加固方法在两种LET值下都达到了抗单粒子瞬态的效果。但是当输入参考时钟频率为1.5 GHz时,由于单元延时的增加,仿真结果显示已经无法实现锁定功能。因此本文的加固方法是在牺牲了一定性能的条件下换取了可靠性的提高。为了对本文的加固效果进一步评估,通过与三模冗余(TMR)[17]方法和交叉耦合负载结构(CCL)[10]进行对比,仿真结果见表1。

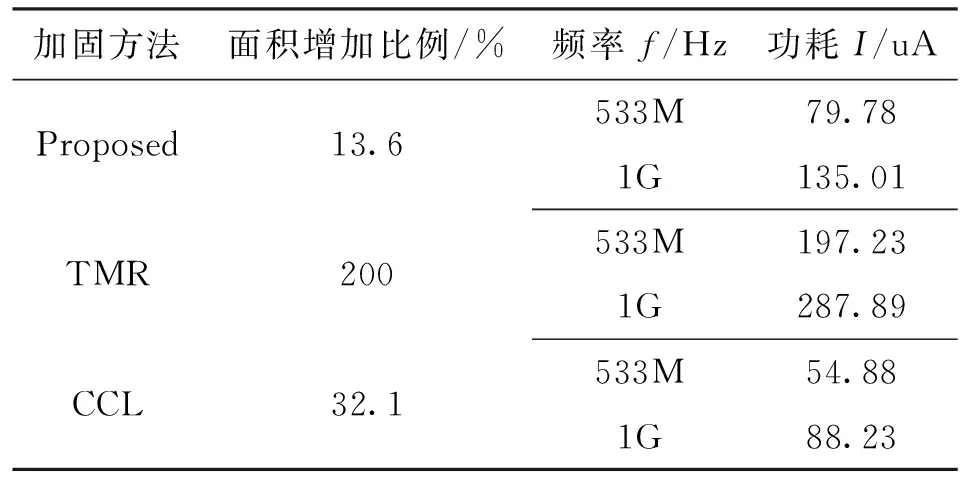
表1 不同加固方法的面积和功耗对比

由于延迟锁相环的输出波形为接近理想的方波信号,因此在实际应用使用三模冗余(TMR)方法几乎可以起到对单粒子瞬态完全免疫的效果,但是其付出的面积和功耗的代价也是最大的;表1给出的交叉耦合负载结构(CCL)方法是在LET值φ1=20 MeV·cm2/mg单粒子入射条件下得到的电路指标,此时电路的SET脉冲宽度已经达到最大。因此综合上述分析,从功耗、面积和抗辐射效果来考虑,本文提出的结构能够达到抗单粒子瞬态效果最佳。

4 结 论

本文首先分析了延迟锁相环的压控延时单元的单粒子敏感性,提出了一种抗单粒子瞬态的加固结构。通过TCAD混合仿真,验证了加固的单级压控延时单元的抗辐射效果,在LET值φ1为20 MeV·cm2/mg的粒子入射条件下,提出的加固结构将电压翻转幅度降低了44.9%;当入射粒子的LET值φ2为80 MeV·cm2/mg时,翻转电压降低幅度为23.7%。Spice仿真表明,加固后的延时单元对锁定状态下的延迟锁相环输出时钟的单粒子瞬态具有很好的抑制效果。因此,本文提出的加固延时单元结构,可用于面向辐照环境的延迟锁相环中。