面向点云无损压缩的快速细节层次优化方法
2021-09-10魏磊万帅王哲诚丁晓斌张伟
魏磊,万帅,2,王哲诚,丁晓斌,张伟
(1.西北工业大学电子信息学院,710129,西安;2.皇家墨尔本理工大学工程学院,VIC3001,澳大利亚墨尔本;3.西安电子科技大学通信工程学院,710071,西安)
近年来,随着3D传感和捕获技术的飞速发展,点云在虚拟现实、自动驾驶、数字城市和3D打印等领域得到了广泛的应用[1-2]。作为一种新型空间数据类型,点云非常适合用来表示3D模型和空间,并且可以非常高效地用于计算和处理,已经成为了一种用于显示和存储三维信息的流行方法。点云是由三维空间中一系列非均匀采样的点组成的,每个点除了空间坐标外,还附着有若干属性信息,比如颜色、反射率和法线等,因此点云具有数据量巨大的特点,为其处理和传输带来挑战。高效的点云压缩是点云相关应用实用化的关键,通常将几何信息和属性信息分别进行压缩。
针对点云的属性信息的压缩,目前已经提出了多种有效的方法。文献[3]提出了一种用于编码点云中属性块的图形变换方法,要求将点云捕捉或排列到规则网格上;文献[4]将点云采样到统一的网格中,然后将网格划分为块以便直接应用图变换,进而进行三维块内预测;文献[5]提出了一种基于图变换的属性压缩方法,利用k近邻扩展生成更有效的图;文献[6]提出了一种基于层次变换和算术编码的点云颜色信息的压缩方法,该变换是一种分层子带变换,类似于Haar小波的自适应变化,已被收于动态图像专家组(MPEG)的基于几何的点云压缩(G-PCC)标准[7]中。另一种重要的基于层次变换的方法为细节层次(LoD),由Clark于1976年首次提出[8],已广泛用于计算机图形的实时3D技术中。目前,关于LoD的工作大多集中在生成方案上:文献[9]提出了一种新的基于二叉树的LoD生成方案;文献[10]提出了一种基于聚类的LoD生成方法;文献[11]则是针对图形学中的几何模型的简化工作;文献[12-13]提出了一种基于距离的LoD生成方法。G-PCC提出了利用LoD对点云属性信息进行压缩的方法,同时为可伸缩编码提供了可能性[7]。文献[14]将LoD与图变换结合,利用图变换对预测残差进行变换编码,进一步去除冗余。现阶段LoD在点云压缩中的主要作用是属性信息的预测编码。
这些文献中的工作并没有解决如何实现最优LoD划分的问题。对于基于距离的LoD,影响编码性能的因素主要有3个:初始采样距离、各层之间的采样距离比和LoD层数[15]。其中,以LoD层数最为关键,除了影响压缩后码率外,还直接关系到编解码时间。本文在理论分析的基础上,建立了基于LoD的预测残差和距离的数学模型,通过该模型对编码性能进行优化;面向点云无损压缩,基于该模型提出了一种通过设置终止阈值优化编码性能的快速方法。
1 点云压缩中的LoD
1.1 LoD及预测
LoD结构是将点云划分为一系列的增强层(Ai)i=1,2,…,N-1和顶端的细节层LN,如图1所示。定义Li为第i个细节层,对Li层进行下采样可以得到更为稀疏的Li+1层,剩余的点则组成i个增强层,即Ai。

图1 LoD金字塔结构Fig.1 LoD pyramid structure
类似于视频预测编码,点云通过预测来去除点之间的相关性,利用特定的预测方式来表征点之间的相互关系。预测编码是指利用已编码的一个或几个样本值,根据某种模型或方法,对当前的样本值进行预测,并将样本真实值和预测值之间的差值进行编码,从而有效提高压缩性能[16]。
在点云压缩中,常用的预测方法是从已编码点中找到若干个距离当前点最近的点作为参考点,将这些参考点的属性重建值进行基于距离的加权平均作为当前点的属性预测值。
与一般的方法相比,基于LoD的预测方法在每个LoD层都具有不同的参考点选择范围,可以分为以下两类:①在对图1中细节层LN进行编码时,其参考点只能在本层中已编码的点中选择,记为细节层的预测;②对于增强层(Ai)i=1,2,…,N-1,不仅可以选择本层中已编码的点,还可以选择此前已编码过的细节层中的点,记为增强层的预测。对于增强层的预测,划分LoD所带来的变化较大。以划分两层来进行说明,如图2所示。对于P3点的参考点选择:在不划分LoD时,预测编码按照原始编码顺序进行,因此参考点都分布在受限于该顺序的方向上,如图2a所示;在划分LoD后,P3位于增强层A1中,其参考点除本层内已编码的点外,还包含已编码的L2中的点,位于空间上的多个方向,如图2b所示。划分LoD的预测通常使得预测的效果更好,从而提升了编码性能。
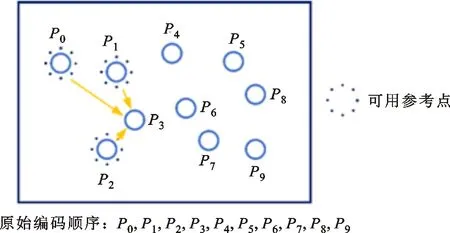
(a)未划分LoD的预测
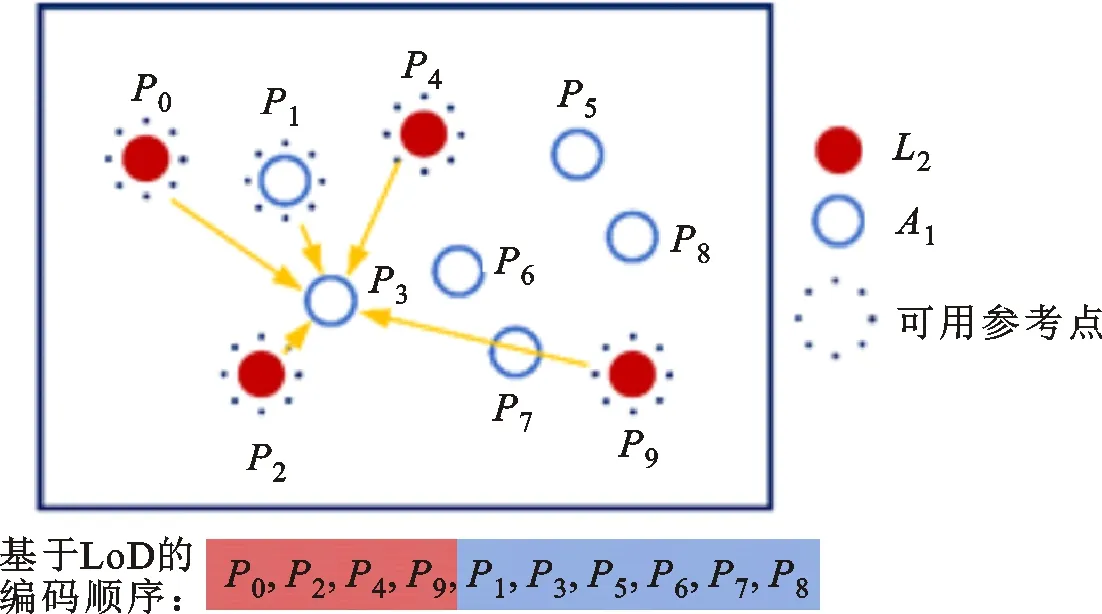
(b)划分LoD的预测图2 未划分LoD及划分两层LoD的参考点范围对比Fig.2 Comparison of the reference points range between the unbuilt LoD and the 2-layer LoD
1.2 预测残差与码率的关系
为了优化LoD的生成,需要获取每一层的码率,而在当前基于LoD的点云压缩方案中,并未对每一层LoD进行独立编码,很难获得其相应的码率,因此本文使用预测残差来代替码率进行建模。
为了研究预测残差的分布情况以及与码率的关系,从G-PCC的静态对象与场景数据库Cat1-A[17]中选择了basketball_player_vox11和dancer_vox11点云作为分析数据集,如图3所示。

(a)basketball_player_vox11 (b)dancer_vox11图3 分析数据集Fig.3 The analysis dataset
对分析数据集进行基于LoD的无损压缩,统计点云中每个点的预测残差情况,并将预测残差的分布拟合为拉普拉斯分布,拟合精度由相关系数的平方(R2)来度量,结果如图4所示。图中,p(e)为概率,e为预测残差。
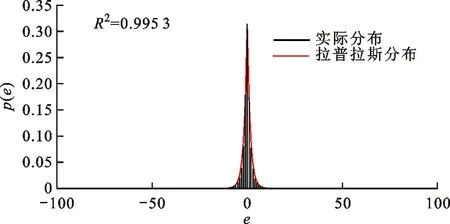
(a)basketball_player_vox11

(b)dancer_vox11图4 预测残差的分布Fig.4 Distribution of prediction residuals
(1)
式中Me为预测残差e的平均绝对误差。
Me和熵是单调递增的关系。因此,将熵或码率的最小化问题转化为Me的最小化问题是合理的。
对分析数据集分别设置不同的参数进行无损压缩,得到码率和预测残差的关系,如图5所示。可以看出,码率随着Me的增大而增大。所以,本文利用Me的最小化来等效码率的最小化是可行的,与理论推导一致。

(a)basketball_player_vox11
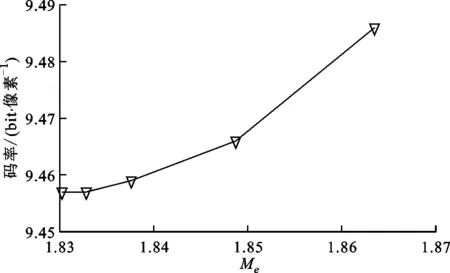
(b)dancer_vox11图5 预测残差与码率的关系Fig.5 Relationship between prediction residual and bitrate
在LoD划分中,每一个细节层相当于对原始点云不同程度的均匀采样,其预测残差也服从拉普拉斯分布。以点云basketball_player_vox11为例,细节层L3的预测残差分布及拟合结果如图6所示。
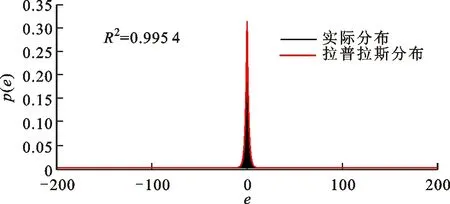
图6 basketball_player_vox11细节层L3的预测残差分布Fig.6 Distribution of prediction residuals in the detail layer L3 of basketball_player_vox11
对于增强层中的预测残差的分布,以点云basketball_player_vox11为例。增强层A6和A8的预测残差分布及拟合结果如图7所示。可以看出,对应的增强层的预测残差也服从拉普拉斯分布。因此,本文使用各LoD层的预测残差来代替码率进行建模。
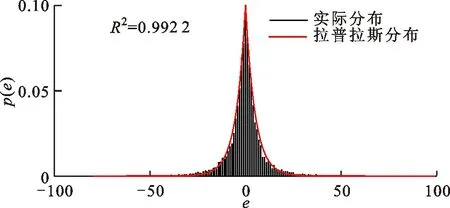
(a)增强层A6

(b)增强层A8图7 basketball_player_vox11增强层的预测残差分布 Fig.7 Distribution of the prediction residuals in the refinement layers of basketball_player_vox11
2 预测残差模型及性能优化
2.1 预测残差模型及性能分析
LoD对点云压缩性能的影响来自于不同的预测方式,因此本小节主要针对此问题进行分析。
以LoD第一次划分为例,在经过一次采样后,点云被划分为了细节层L2和增强层A1。按照LoD的顺序,首先对L2中的点进行预测编码,其可用参考点仍然具有原始点云的特点,即位于受限于编码顺序的空间方向上。同时,又由于经过采样,相邻点之间的最小距离变大,使得它们之间的相关性减弱,导致预测的效果变差,从而造成编码性能的损失。对于其后进行编码的A1中的点,参考点不仅可以选择本层中已编码的点,还可以选择已编码的L2中的点,因此参考点的可选范围更大,且位于空间中的多个方向,同时相邻点之间的最小距离与原始点云一致,由此提高了预测的准确度,提升了编码性能。对于整个点云,若A1的性能增益大于L2的性能损失,则LoD划分可以提升预测编码性能。
为了准确分析LoD划分前后的性能变化情况,利用预测残差建立数学模型。设A1中的点数占L1(原始点云)的比例为r1,那么L2占L1的比例则为1-r1。L1在划分LoD后的预测残差平均绝对误差可以表示为
(2)
式中:EL2为L2的预测残差平均绝对误差;EA1为A1的预测残差平均绝对误差。
与不划分LoD时L1的预测残差平均绝对误差(记为EL1)相比,预测残差的变化记为Δ1,有
(3)
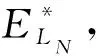
(4)
式中:rN为AN占LN的比例;ELN+1为LN+1的预测残差平均绝对误差;EAN为AN的预测残差平均绝对误差。
LN的预测残差变化ΔN可表示为
(1-rN)(ELN+1-ELN)+rN(EAN-ELN)
(5)
式中ELN为LN未进一步划分LoD时的预测残差平均绝对误差。
令δ1=ELN+1-ELN,δ2=EAN-ELN,可得
ΔN=(1-rN)δ1+rNδ2
(6)
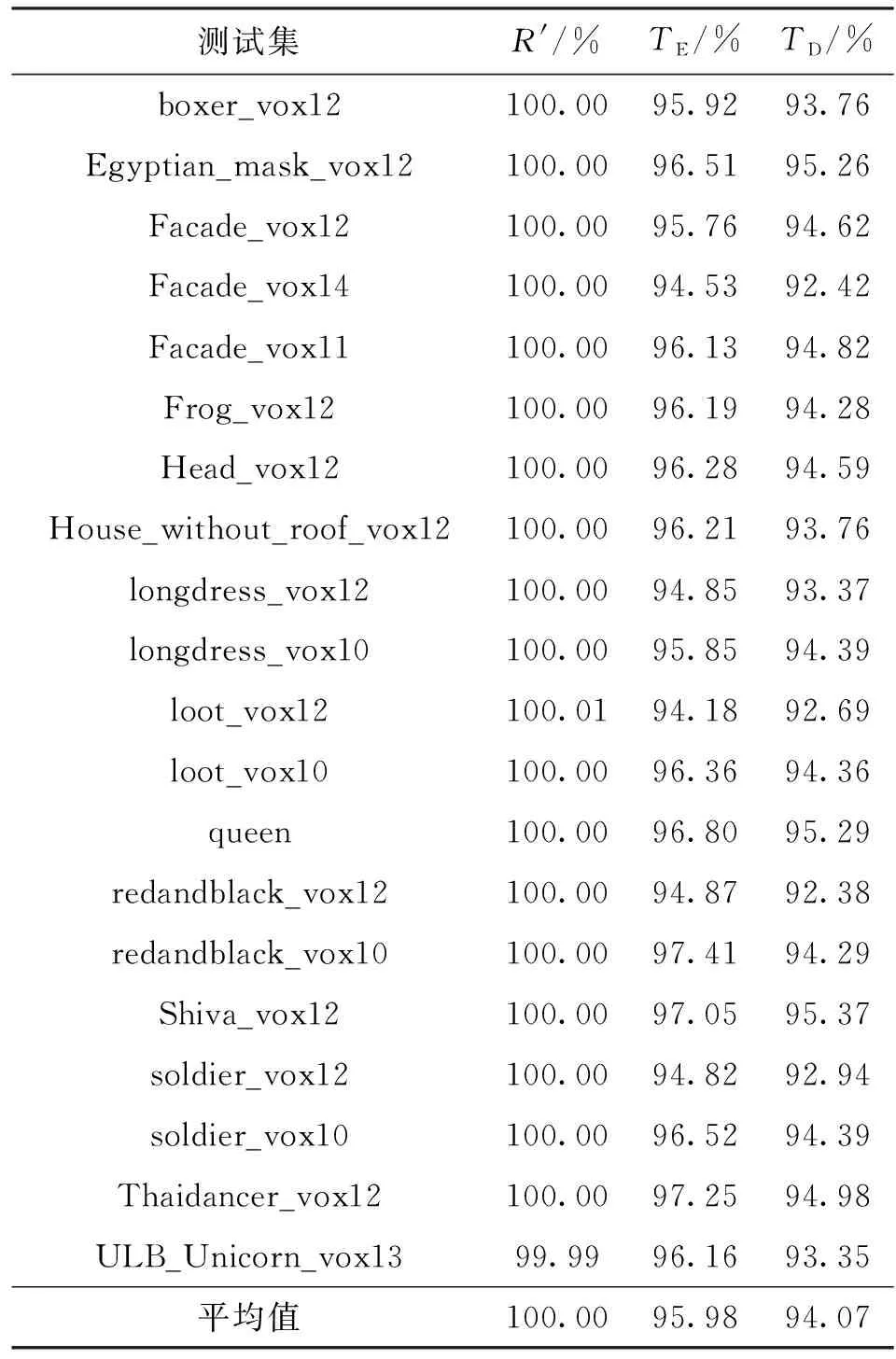
由于LN+1是对LN的采样,因此LN+1中相邻点之间的距离要大于LN,其相关性更差,有δ1>0,即随着LoD的划分,新的细节层通常会有性能的损失。对于δ2,可以认为是AN中的点使用何种预测方式最优的问题。根据2.1小节前半部分中的分析,对于增强层的预测方式,参考点的分布更加广泛并且具有全向性,可以提高预测的准确度和编码性能,因此EAN 综合分析δ1和δ2带来的性能变化可知,式(6)为0时的编码性能最优,此后的划分都不会带来编码性能的增益,反而会造成性能损失,如图8所示。 图8 ΔN与划分层数N的关系Fig.8 Curves of ΔN vs. number of LoD layers N (7) 式中pN为LN中的点占全部点的比例,公式为 (8) 其中ri为Ai占Li的比例,与初始采样距离和各层之间的采样距离比有关。 当式(7)为0时,编码性能达到最优。为了求解最优值,需对两种预测方式下的预测残差进行拟合。 由空间相关性可知,预测残差与距离相关,因此将它们表示为距离的函数。对于细节层Lj,设 ELj=f(d1,j)(j=1,2,…,N) (9) 式中d1,j是Lj中相邻点之间的距离。 对于增强层Ai,设 EAi=g(d2,i)(i=1,2,…,N) (10) 式中d2,i是Ai中相邻点之间的距离。 点云dancer_vox11两种预测方式的对比如图9所示。将ELj和EAi的拟合结果代入式(7),可得 图9 dancer_vox11中两种预测方式的对比Fig.9 Comparison of prediction methods in dancer_vox11 (11) 式中:d1,N和d1,N+1分别为细节层LN和LN+1中相邻点的距离;d2,N为增强层AN中相邻点的距离。 将式(6)代入式(7),可得 (12) 由于当前基于LoD的点云压缩方案适用于均匀采样或者平滑的点云,对于非均匀采样和噪声点云并不适用[15],因此本文主要针对均匀采样或者平滑的点云,并由此简化2.1小节中所建立的模型式(11)。 在实际中,点云中的点都位于物体表面,因此在较小区域内点云可以被视为二维平面,如图10所示。 图10 点云表面小区域内点的分布示意Fig.10 Points in a small region of surface in point cloud 在G-PCC中,相邻两次采样距离比都固定为2[7],因此除第一次采样比r1以外,其余每次采样比ri(i>1)都几乎相同,约为3/4。式(11)可以简化为 (13) 图与划分层数N的关系Fig.11 Graph of and the number of LoD layers N 图12 所提方法流程Fig.12 Flow chart of the proposed method 对点云进行LoD划分,在每一层的采样结束后,计算当前细节层Li占原始点云的比例,并判断是否小于终止阈值θ。若小于θ,则结束LoD划分,进行预测编码;若不小于θ,那么判断当前LoD层数i是否小于编码端预设的LoD层数N,若小于,则继续LoD划分,否则结束划分,进行预测编码。 在第3节中,进行了大量的实验来评估所提方法。实验选取了G-PCC的静态对象与场景数据库Cat1-A[18]作为测试集(分析数据集中的点云除外),这些点云也被广泛应用于评估各类点云压缩方法性能的实验中[6,18-20]。 为了评估压缩的性能,本文对比了码率比R′、编码时间比TE、解码时间比TD共3种指标。码率比R′的计算公式为 (14) 式中:Rp是点云按照所提方法进行无损压缩后的属性码率;RG为点云根据G-PCC的通用测试条件(CTC)进行无损压缩后的属性码率。 编码时间比TE为所提方法的编码时间与G-PCC(参数参照CTC设置)的编码时间的比值;解码时间比TD为所提方法的解码时间与G-PCC(参数参照CTC设置)的解码时间的比值。 将所提方法与G-PCC(参数参照CTC设置)进行比较,对测试集使用G-PCC TMC13 v9点云压缩平台[7]进行无损压缩,结果如表1所示。可以看出,当阈值θ=0.003时,与设置为CTC时相比,码率没有增加,而编解码时间则显著减少,平均节省了约4%的编码时间和6%的解码时间。 表1 所提方法与CTC的性能对比 对于绝大多数点云,在通过本文阈值终止LoD划分时,其性能已经达到最优,与CTC一致,因此码率比R′为100%。若进一步划分LoD,新的细节层中相邻点的距离呈指数增大,使得其相关性急剧下降,性能损失较大;对于新的增强层,虽然对改善预测的准确性有一定的效果,但所带来的增益与细节层的损失相互抵消,因此无法进一步减小码率。同时,这部分点的比例又足够小,两个因素综合起来使得压缩后的码率维持不变,达到最小。 对个别的点云,码率比R′略微大于100%,例如loot_vox12的100.01%,表明所提方法的码率大于CTC的码率。这是由于本文方法使用了统一的阈值,可能造成一定的误差,使得LoD较早结束了划分。此时,最顶端的细节层中的点还存在一定的相关性,若再继续划分LoD,还会有一定的性能增益,但是由于这部分点的数量已经非常少,根据2.1小节中的分析,其影响也非常有限。 另外还有一种很少见的情况,例如ULB_Unicorn_vox13的码率比R′小于100%,即此时本文方法的码率小于CTC的码率。这类点云的内容较为复杂,相似点大多集中在较小的范围内,如图13所示。 图13 ULB_Unicorn_vox13点云Fig.13 Point cloud ULB_Unicorn_vox13 在达到阈值后,若再进一步划分LoD,由于新的细节层中相邻点的距离呈指数增大而使得其相关性急剧下降,性能损失较大。另一方面,新的增强层对提升预测准确性的效果甚微,甚至反而会降低预测准确性,因此本文方法性能会有一定的下降,码率比R′小于100%。 表2对比了CTC中的LoD层数NG和本文方法实际划分的LoD层数N*。可以看出,对于测试集的每一个点云,N*都远远小于NG,因此避免了不必要的LoD划分过程,节省了宝贵的编解码时间。 表2 LoD层数对比 本文提出了通过设置终止阈值优化LoD划分的方法,无需考虑各层LoD的采样距离。实验中使用的阈值仅是通过两个分析点云进行简单统计得到的,将其用于均匀采样或者平滑点云的测试集已经获得了较好的效果。当然,阈值的设置并不仅限于此,可以通过更多的训练得到更优的阈值。 本文针对基于LoD的点云无损压缩,通过分析LoD中增强层与细节层的预测方式对编码性能的影响,并结合空间相关性的原理,建立了基于预测残差的LoD优化模型。在实际应用中,特别是对编码端的实时性要求较高的场合,对每个未知点云都进行预编码或在线计算是不现实的,为了降低实现复杂度,本文提出了一种基于均匀采样及平滑点云特性的模型参数简化方法,并在此基础上实现了一种基于阈值的LoD划分快速方法。实验结果表明,在通用测试条件下,所提方法与G-PCC相比,在码率未增加的同时,节省了约4%的编码时间和6%的解码时间。 本文方法避免了对点云进行预编码或在线计算的复杂过程,提高了所建模型的实用性。仅通过阈值控制实现LoD的性能优化,在达到最小编码码率的同时避免了无效的LoD划分,节省了编解码时间,提高了点云压缩的实时性。 下一步将研究快速和高效的预编码和在线计算的方法,实现对任意未知点云编码性能的自适应优化。另外,本文所建立的模型并不仅限于点云的无损压缩,还可扩展至点云有损压缩的率失真优化。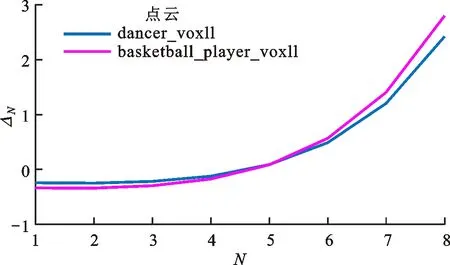


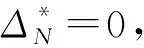

2.2 面向点云无损压缩的快速LoD划分方法




3 实验与分析
3.1 数据集
3.2 评价指标
3.3 结果分析


4 结 论
